分布式能源资源的通用数字孪生体构建与模拟方法
原启涛,李志勇,燕续峰,肖居承,何光宇
(1.上海交通大学 电力传输与功率变换教育部重点实验室,上海 200240;2.海南省电力学校,海南 海口570203)
0 引言
分布式能源资源(DER)包含可控负荷、分布式光伏、风机、储能等,有效利用DER不仅能够平抑波动和降低系统峰谷差,而且具有可观的社会效益和经济效益[1]。随着DER数据源的异构性、海量性、随机性趋于复杂,通过物理建模方法估量其运行稳态和暂态的难度和成本越来越高[2]。
数字孪生(Digital Twin,DT)为DER的模拟测试和运行优化提供了新的思路[3]~[5]。文献[6]~[9]设计了电力系统DT的系统框架、组建模块、通信架构和规约及应用案例。文献[10]指出提出了负荷DER功率变化转移模型,描述了电器状态、功率与事件的关系。文献[11]提出了以数据采集-事件检测-特征提取-负荷分类-负荷识别为流程的负荷模型构建方法。文献[12]则关注于负荷DER的高频特征,如暂态电流、电压-电流轨迹等,借此刻画负荷DER的运行特性。文献[13],[14]提出了基于超状态概念的负荷运行状态模型及改进方法,极大地简化了模型并提高了求解效率。文献[15]提取了负荷DER的开启、关闭时间和持续时长等关键因素作为额外特征用于负荷模型构建。文献[16]针对一阶隐马尔科夫 (Hidden Markov Model,HMM)模型弱时间特性的特点,提出了一种负荷DER的时间特性模型,更直观地表述了用户用电习惯。对于分布式光伏、风机、储能等DER,现有文献主要针对其供电特性进行建模与研究。文献[17]针对光伏等新能源出力的不确定性,提出了一种基于变分自编码器和条件生成对抗网络联合结构的不确定性建模方法。文献[18]采用改进的遗传算法建立了实际双馈风电机组的全运行工况下快速启动的精确电磁暂态仿真模型。文献[19]运用戴维南定理和模拟受控电流源对储能电站进行等值仿真建模。上述文献大多针对某一类DER进行建模,缺乏一种通用的DER模型对其稳态运行特性及暂态转移过程进行统一精准描述,也缺乏相应的DER数字孪生体模型的运行模拟方法。
本文提出了DER的通用数字孪生体构建及模拟方法,并通过功率模型对稳态进行统一分解与描述,建立了多类暂态概率矩阵,对DER暂态过程及产生条件进行统一描述,给出了通用的DER数字孪生体模型及其运行模拟方法。算例对常见的DER进行了运行模拟测试,验证了所提方法的有效性。
1 DER数字孪生体的通用稳态模型
1.1 DER稳态的功率成分
根据WOLD分解定理[20],DER运行功率分解为规律成分和噪声成分。DER的功率曲线P(t)为

1.2 DER通用稳态模型
本文将DER稳态功率定义为规律成分和噪声成分的叠加结果,应当对这两种成分区别建模。
1.2.1 DER稳态功率的规律成分建模
①线性规律模型
DER线性规律模型为

1.2.2 DER稳态功率的噪声成分建模
将DER功率解耦为规律成分和噪声成分后,其中的噪声成分会受到各类外生、内生因素的影响,当随机因素独立时,依据中心极限定理,可近似认为噪声成分服从高斯分布[21],即:

式中:m为噪声成分的平均值;s为噪声成分的标准差。
2 DER数字孪生体的通用暂态模型
2.1 DER暂态模式
DER的运行是稳态与暂态交替出现的,通常暂态过程持续时间很短,DER绝大部分时间处于稳态运行[20]。因此,暂态主要指DER稳态间的转移,同时包含了其间的过渡态过程。根据影响暂态的主体可以将DER的暂态模式分为外界主导和自身主导两类。
2.2 DER通用暂态模型
针对传统HMM的弊端,本文提出DER通用暂态模型,包括暂态概率矩阵T、时长型暂态概率矩阵T1、时刻型暂态概率矩阵Tt及频次型暂态概率矩阵Tf等部分,以全方位地描述各类DER在各种情况下的暂态转移概率,以便于支撑数字孪生的平行测试功能。
2.2.1 暂态概率矩阵暂态概率矩阵T=[tij,1≤i,j≤N]刻画了DER在暂态过程中转向各种稳态的转移概率。不同于传统HMM中的转移矩阵,在本暂态模型中,暂态概率矩阵T的对角元均为0,即不考虑DER的自身向自身稳态的转移(即不转移)的情况,因为已经发生了暂态是T的前提。

从DER的T矩阵中,可以看出暂态的所有情况及对应的发生概率,但是仍缺乏信息描述DER会在何种条件下发生暂态。由于DER的暂态具有很强的时间相关性,因而还须从时间概率的角度上描述DER的暂态情况。
2.2.2 时长型暂态概率矩阵
考虑到DER运行规律性和运行模式的固定性,稳态持续时间的变化将保持在一定范围内。本文提出时长型暂态概率矩阵T1,以描述DER暂态转移的持续时间概率分布。用高斯分布对该暂态过程进行建模,时长型暂态概率矩阵T1的数学表达式为

2.2.3 时刻型暂态概率矩阵
转入型稳态通常由外界主导,通常一种时刻型稳态的转移可以在一天的不同时段内发生多次,通常具有多峰性。由于高斯分布刻画这种行为将产生极大的失真,因此,本文采用高斯混合模型(Gaussian Mixture Model,GMM)对时刻型DER的稳态转移时刻分布进行建模。高斯混合模型形式为

式中:G(θij)为时刻型稳态i向稳态j型转移时刻高斯混合模型;θij为模型参数;Si为由所有转入型稳态构成的集合,类似的So为转出型稳态集合。
Tt的元素G(θij)分布以1 d为周期,描述了DER从稳态i切换至稳态j在1 d时段上的概率分布。
2.2.4 频次型暂态概率矩阵
利用Tt可以描述用户对某些DER时的使用习惯,但其中的GMM以1 d为周期,其只能反映用户在1 d之内使用DER的时间偏好,而不能反映1 d内用户使用DER的次数和频度。本文提出频次型暂态概率矩阵Tf,用于刻画用户1 d内使用DER而产生的暂态的频率次数,其数学表达式为
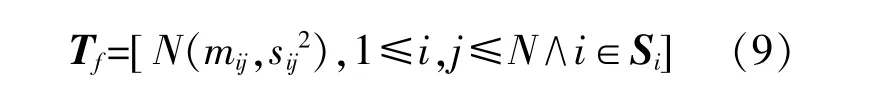
式中:N(mij,sij2)为DER在1 d内从i稳态转移至j稳态的频率高斯分布。
3 DER数字孪生体的运行模拟方法
3.1 DER的通用数字孪生体模型
稳态模型参数反映了DER稳态内功率变化情况及对应物理作用,其研究的时间尺度小,以解析模型为主,可以准确刻画DER功率;暂态模型参数反映了用户及DER的行为规律,研究时间尺度大,以概率模型为主,可以推断DER暂态事件的概率。模型两部分相互影响、交替产生作用,共同描述了DER的运行规律。基于DER的数字孪生体模型可以实现多种应用功能。利用稳态模型参数可以实现DER的功率短期预测、DER的状态识别、异常状态监测、用电数据压缩和运行模拟等功能。DER的暂态模型参数可以实现DER功率的长期预测、用户用电行为分析等功能。
3.2 通用数字孪生体模型参数提取
3.2.1 稳态模型参数提取
稳态参数包括稳态数量N、各稳态的趋势功率模型S(t)、干扰噪声模型e(t)。根据功率片段聚类方法可确定稳态数量N及每个稳态对应的功率片段样本。
各稳态的趋势功率模型S(t)及干扰噪声模型e(t)提取方法如下。
①对于DER的某一个稳态n,属于该稳态的功率片段样本集合为P(n)=[P1(n),P2(n),…,Pm(n)],集合中稳态n的样本按照序列长度递减排序,P1(n)为稳态n持续时间最长的功率序列,并指定该序列初始点对应时刻t=0,进而得到该序列任意点对应的时刻。将其他所有的序列样本与该序列对齐,得到其他各序列对应得初始时刻,进而可以得到序列任意功率点对应的时刻。
②在得到了样本集P(n)中每一个功率点对应的时刻后,可以获得DER稳态n的时间-功率样本点集Pc(n)=[(t1,p1(n)),(t2,p2(n)),…,(tm,pm(n))]。选取拟合误差最小的模型作为DER稳态模型。
③利用S(n)(t)对时间-功率样本集中的点进行模型估计,可以得到样本估计偏差Pe(n)=[P(n)1,error,P(n)2,error,…,P(n)m,error]。 对偏差样本进行正态分布拟合即可得到稳态n的干扰噪声模型e(n)(t)。
3.2.2 暂态模型参数提取
暂态模型参数包括暂态概率矩阵T、时长型暂态概率矩阵T1、时刻型暂态概率矩阵Tt、频次型暂态概率矩阵Tf与转移类型集Si及So。DER的转移类型可以在人工标注实际物理工作稳态时一并完成,进而得到Si及So。
①暂态概率矩阵T
初始化T为零矩阵,根据DER历史运行记录找出所有的稳态转移,形成DER的稳态转移样本集St=[(1→i,t1),…,(i→j,tn),…],其中i→j表示DER从稳态i切换至稳态j的转移,tn表示这次稳态转移发生的时刻。对于St中的每一次稳态转移,令暂态概率矩阵T中的元素tij=tij+1。在遍历了稳态转移样本集St中每一个元素后,对T的每行进行归一化:

式中:Ti为稳态i向其他稳态转移的频率行向量。
②时长型暂态概率矩阵T1
对于转出型稳态n,可以由其功率样本集P(n)=[P1(n),P2(n),…,Pm(n)]得到该稳态的持续时间集T1(n)=[T11(n),T12(n),…,T1m(n)]。 提取持续时间集的均值及方差得到该稳态时长型暂态概率分布T1n=N(mn,sn2)。
③时刻型暂态概率矩阵Tt
对于转入型稳态i,从中找到所有由该稳态转移至其他稳态的子样本集St(i)=[(i→j,t1),…,(i→k,tn),…]。并根据St(i)中转入稳态的情况进一步将其划分为多个同类型稳态转移的子样本集St,j(i)=[(i→j,t1),…,(i→j,tn),…],S(i)t,j+1,…,j=1,2,…,n,j≠i。
同类型稳态转移子样本集St,j(i)包含所有稳态转移i→j发生的时刻样本。由于转入型稳态转移时刻分布以一天为周期,因此需要对集合里的时间元素进行处理,得到只包含24时计时的同类型稳态转移时间集St,j(i)=[t′1,t′2,…,t′n]。用GMM对其中的元素进行拟合,获得稳态转移i→j的转移时间概率分布G(θij)。
在采用GMM拟合时采用α-EM算法[22],[23],对每个同类型稳态转移子样本集进行拟合后,得到转入型稳态i的时刻型暂态概率分布矩阵Tt,i=[G(θij),j=1,…,n,j≠i]。
④频次型暂态概率矩阵Tf
频次型暂态概率矩阵Tf刻画DER在一天的周期内发生稳态转移的次数。同类型稳态转移子样本集Stj(i)包含所有稳态转移i→j发生的时刻样本。对集合里的时间元素进行处理得到稳态转移i→j在历史记录的时间范围内每日的转移频数集合Stj″(i)=[cd1,cd2,…,cdn]。提取集合内元素的均值方差得到该稳态转移i→j的频率分布N(mij,sij2)。
在对每个同类型稳态转移子样本集进行了拟合后可以得到转入型稳态i的转移频率矩阵Tf,i=[N(mij,sij2),j=1,…,N,j≠i]。
3.3 DER数字孪生体的运行模拟方法
DER数字孪生体的运行模拟在DER灵活性感知、评估、挖掘、调控和促进新能源消纳等方面具有重要作用[12],[24],[25]。同时,DER运行模拟产生的数据还可以扩充已有数据集大小,用于机器学习模型的训练,模拟生成的DER运行数据,在某些条件下还具有正则化效果[26],有利于降低机器学习模型预测的误差。
本文提出DER数字孪生体的运行模拟算法,能够模拟未来待预测时间段内DER稳态持续和暂态转移情况,进而通过各稳态的功率模型生成预测功率。图1展示了DER运行模拟算法的流程。

图1 DER数字孪生运行模拟算法流程图Fig.1 Flow chart of DER digital twin operation simulation algorithm
4 算例测试
本文以分布式能源资源中占比较高的空调负荷为例,说明提出的数字孪生体构建及模拟过程,并对所提方法对典型DER(风、光出力和充电桩的放电功率)进行模拟,其对比数据源于PJM开源数据集。基于本文所提出的DER通用数字孪生体模型及其运行模拟方法,生成1 d的DER运行模拟数据。
4.1 构建及模拟过程
某定频空调5 d的历史功率曲线如图2所示。

图2 某空调5 d的历史功率曲线Fig.2 5 day historical power curve of an air conditioner
采样频率为15 s/次,由于采集时间为夏季,故提取的空调稳态不包含制热。利用历史运行功率数据得到的该空调模型的稳态参数如表1所示。

表1 空调模型稳态参数Table 1 State parameters in air conditioner's model

由图3可以看出,空调平均每次制冷时间在10 min左右。从时刻型暂态概率和频次型暂态概率分布来看,空调稳态转移的次数平均约为23次/d,运行时间分布在9~23时内。

图3 空调模型的暂态参数Fig.3 Transient parameters of air conditioning model
图4为前文提出的运行模拟算法得到的功率曲线与空调历史数据中最接近的功率曲线对比。图中模拟数据与历史数据之间的绝对误差为5.3%。
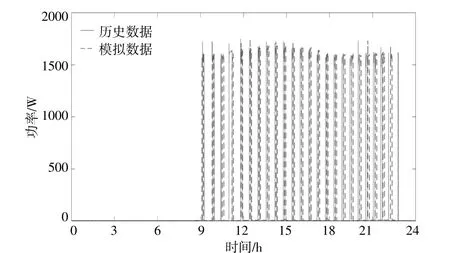
图4 空调数字孪生运行模拟结果Fig.4 Simulation results of air conditioning digital twin operation
由图4可以看出,由模拟算法得到的功率曲线大体上准确模拟了空调典型周期运行的特点。
4.2 DER运行模拟测试
在运行环境为Inter CORE I7 8th Gen,各个模拟时间均在1 s内,采用本文所提出的数字孪生运行模拟算法生成了其他几种常见DER的功率曲线,并与其历史数据的对比,如图5所示。

图5 DER数字孪生运行模拟结果Fig.5 Result of DER digital twin operation simulation
由图5可知,各子图中模拟数据与其最接近的历史数据之间的绝对误差分别为4.3%,4.1%和3.7%,验证了所提方法的有效性,表明所提算法时效性可支撑实时运行模拟。由模拟方法生成的DER运行数据与DER实际历史运行数据相比,在开始时间、持续时间及稳态功率等方面曲线形态均十分接近,具有良好的相似程度。本文方法不仅能够在大体上准确模拟光伏出力昼盈夜亏、风机的反调峰特性、充电桩的典型时空分布情况,而且在细节的运行模拟上(例如噪声成分幅值、稳态功率波动幅度、暂态过渡功率)也与历史数据具有较高的相似程度。该算例测试结果可以说明本文所提出的DER数字孪生体模型及其运行模拟技术能够支撑数字孪生世界的高精度镜像映射和平行测试功能。
5 结语
本文对DER通用数字孪生体模型进行了详细分析,对DER稳态的功率成分进行了分析并建模;随后对DER暂态进行了研究并建模,从而辅助电力系统调控中定制有序的发用电计划,减少弃风弃光,促进可再生能源的大规模消纳。后续研究将基于所提出的通用数字孪生体模型,构建虚拟的智能用电网络人机交互平台;基于数字孪生技术,直接基于真实系统数据来模拟各种运行策略下系统运行情况,并评价运行策略的经济性和安全性等,以提高可再生能源的消纳为目标,指导真实系统的运行调度,为实际运行直接提供参考。

