计及综合需求响应和不确定性风险的电气热耦合型微电网协同优化

戎泽坤，陈佳佳，赵艳雷，肖传亮

（山东理工大学 电气与电子工程学院，山东 淄博 255000）

0 引言

随着化石燃料的逐渐枯竭和环境污染的加剧，全球能源结构面临巨大挑战，需要进一步调整能源生产和消费方式。为有效利用可再生能源、提高微电网运行效率，能源领域对多能耦合型微电网的研究不断深入[1]，[2]。

多能耦合型微电网是传统微电网概念的延伸，而随着能源耦合程度的加深和各种能源转换设备的增加，多能耦合型微电网的优化配置方式和运行策略成为复杂又亟待解决的问题，目前研究多集中在多能耦合型微电网的系统建模、能量优化、规划设计等方面。文献[3]提出了关于多能微电网中热电联产系统容量大小的优化部署，可以最大限度地减少CO2排放总量和净成本。文献[4]提出了一种用于综合电、热和冷的微电网系统两阶段优化规划和设计方法。第一阶段选择最优设备容量，第二阶段解决最优调度问题。然而，由于大规模风电并网、多种能源之间的转换使多能微电网的调度变得更加复杂，上述文献缺乏对负荷需求侧管理和不确定风险的考虑和分析。作为一种具有成本效益的灵活资源，负荷侧的需求响应受到越来越多的关注，需求响应可以有效降低负荷波动，促进可再生能源消纳，增强电力系统运行灵活性[5]。但是传统的电力需求响应主要是通过削减或转移负荷，这往往会影响用户的用电体验，导致用户参与需求响应积极性不高，不能完全激发用户的可调负荷响应潜力。随着燃气轮机、热泵和电转气（Power to Gas，P2G）等设备的利用，电力、天然气和热力系统在多能耦合型微电网中紧密相连，综合需求响应（Integrated Demand Response，IDR）应运而生。IDR在满足电网调峰需求的同时，使用户几乎不改变能源使用习惯，通过替代能源使用保证用户用能满意度[6]。文献[7]提出了IDR的概念，研究多能源网络与能源供应商之间的交互策略，仿真结果证明了IDR与传统电力需求响应相比在能源的灵活转换、提高用户用能体验方面有很大的优势。本文在多能耦合型微电网中考虑电、气负荷的IDR，充分利用可再生能源、储能、能源转换设备，有效激发用户参与IDR的积极性。但是，现有研究IDR的文献大多没有考虑可再生能源并网带来的不确定风险，这对微电网稳定运行有很大的影响。风电作为具有良好发展前景的可再生能源发电方式，近年来得到了迅速发展[8]。然而风力发电的随机性和波动性使多能耦合型微电网的不确定风险增大，这成为影响风电大规模消纳的主要因素。因此，对风电并网型微电网风险评估方法的研究显得尤为重要。文献[9]通过风电预测，采用随机机会约束规划研究了动态优化调度问题，但忽略了风电的模糊性。

本文首先在利用可再生能源、储能和能源转换设备的基础上，构建了基于价格的IDR；然后通过考虑风电的模糊特性与随机特性，提出基于可信性理论的不确定风险模型，进而建立了考虑IDR和不确定性风险的电气热耦合型微电网协同优化模型[10]，[11]；最后，基于（Evolutionary Predator and Prey Strategy，EPPS）算法求解模型，旨在提升微电网运行效率，充分挖掘需求侧电、气负荷灵活性和实现不确定风险与成本之间的最优权衡。

1 多能耦合型微电网的结构与模型

图1为多能耦合型微电网的电能量流、天然气能量流和热能量流。包含能源供应模块、能源转换模块和负荷需求模块。

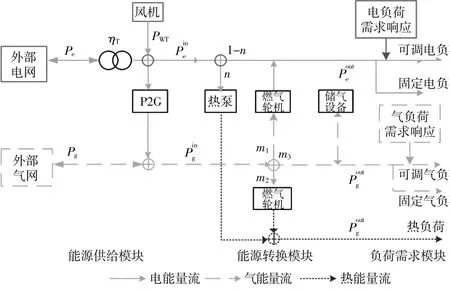
图1 多能耦合型微电网的能量流模型Fig.1 Energy flow model of multi-energy coupling microgrid

式中：Le，Lg，Lh分别为用户消耗的电、气、热负荷；Le，CL，Lg，CL分别为用户可调的电负荷和天然气负荷；Le，NL，Lg，NL分别为用户固定电负荷和天然气负荷。

2 考虑IDR和不确定性风险的协同优化模型

2.1 IDR模型

为便于表述，本文以电负荷为例来描述基于价格的IDR模型。在IDR中，采用弹性系数矩阵描述电力或天然气价格增减时的负荷需求变化量，电负荷的弹性系数矩阵为

若t=t′，E（t，t′）为自弹性系数，否则E（t，t′）为交叉弹性系数。自弹性是指负荷不能转移到其他时段，只能接通或断开负荷才能参与需求响应；而交叉弹性是指负荷可以从高峰时段转移到非高峰期时段。

需求响应模型通常分为基于激励和基于价格的两种模型。本文考虑基于价格的需求响应模型，即价格在不同时期有所不同，因此它会激励用户改变消费模式。基于价格的需求响应具有一定的不确定性，因为外部环境的不确定性、信息延迟、决策主体在响应过程中的感知偏差，使得用户对导致系统出现的价格变化有一定的响应偏差、反应不足或反应过度，然后根据价格弹性系数矩阵，得到电负荷的需求响应模型。

式中：Eg（t，t′）为气负荷的价格弹性矩阵；L′g（t），ρg（t′）分别为t时刻实施IDR后，用户对天然气的需求和天然气价格。

2.2 不确定风力发电风险评估模型

风力发电的预测误差一直存在，但是在以小时为周期的短周期调度中，可以假设风速预测误差服从高斯分布[12]。另外，由于风速预测误差受到温度、天气的影响，风电的实际预测值具有模糊性。因此，本文将不确定风电视为模糊随机变量，提出了一种基于可信性理论的风险评估模型来定量分析不确定风电给微电网带来的风险。

可信性测度是一种自对偶的测度指标，用于描述模糊事件的可信性。风电预测误差百分比εw可表示为

式中：Ew+和Ew-分别为正错误率和负错误率的统计平均值；σ为权重。

预测误差可分为两类：一是实际值高于预测值的正误差；二是实际值低于预测值的负误差。

对式（8）进行求导，得到可信性模型为

2.3 目标函数

多能耦合型微电网协同优化的目标是在保证系统安全性的前提下最大限度地利用调度范围内的风电资源。另外，成本是电力系统应该考虑的主要因素之一，它关系着电网运行的经济性能。但是由于风电的不确定性，必须对风电渗透带来的风险加以考虑。在前文中，本文研究了可信性理论，以实现运营成本和风险之间的最优权衡。多能耦合型微电网每小时运行成本包括从外部电网购买电力成本、购买天然气成本和实施IDR的成本，本文提出的优化模型总目标函数可表示为

2.4 约束条件

目标函数需满足以下约束条件。

①功率平衡约束

多能耦合型微电网负荷需求包括电、气、热负

③能源供给模块，供能侧输出受机组输出参数上、下限的约束

④能源转换模块约束

热泵通过消耗电能提供热量，热泵的输出-输入、燃气轮机输出极限、储气设备满足约束条件分别为

式中：Xt为可控制负荷的状态值，取值为-1，0，1，分别表示附着在移出、不转移和移入的状态；Le，CL，t和Lg，CL，t分别为t时段参与调度的电力负荷和天然气负荷。

2.5 求解方法

EPPS算法是基于动物搜索行为和群体生活理论，建立的一种动态捕食者-猎物模型，该模型能够很好地平衡动物的局部开发搜索能力和全局探索搜索能力。与其他优化算法相比，EPPS在优化多模态、非凸和高维基准方面显示出了优越的适用性；同时电力系统仿真研究表明，EPPS可以获得更优的解。本文利用EPPS算法求解计及IDR和不确定性风险的电气热耦合型微电网协同优化模型，实验流程如图2所示。

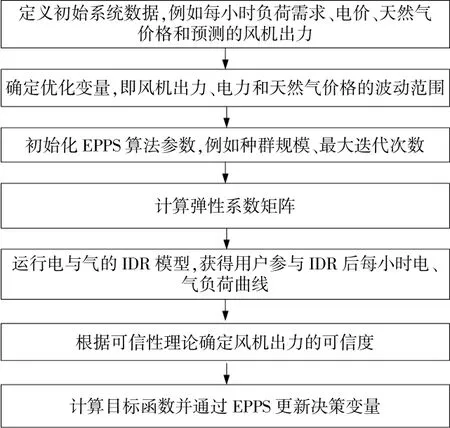
图2 多能耦合型微电网协同优化模型求解流程Fig.2 Block diagram of the solution step of the multi-energy coupled microgrid collaborative optimization model

3 仿真分析

为了验证所提模型的实用性和有效性，本文在一个由5台风机设备和多种能量转换设备组成的多能耦合型微电网上进行了仿真验证。本文采用Matlab优化计算，采用EPPS算法求解所提出的优化模型。在多能耦合型微电网中，本文将初始电价和天然气价格分别设定为0.4元/（kW·h）和0.5元/（kW·h）。权重因子σ取值为2.33。需求弹性定义为需求对价格的敏感性，具体数据如表1所示。

表1 自弹性和交叉弹性值Table 1 Self and cross elasticity values

假设可调负荷占总负荷需求的20%，即80%的负荷需求被认为是不可控。EPPS的种群大小设置为100，EPPS算法最大迭代次数设置为50 000次。

多能耦合型微电网中P2G、燃气轮机、热泵和储气设备的具体参数取值如表2所示。

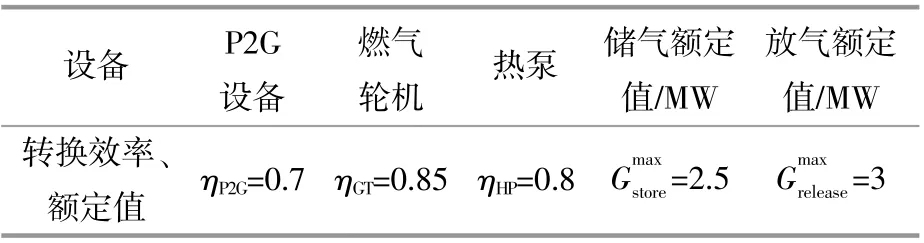
表2 能量转换和储能设备参数Table 2 Energy conversion and energy storage equipment parameters

3.1 P2G及储能设备对多能耦合型微电网调度的影响

传统的能源系统运行仅限于热、电、气等单一能源系统，不能充分利用多能互补优势和协同效应。在多能耦合型微电网中，P2G是一种间接利用风电的方式，当风机出力在满足电负荷需求之后有剩余时，将多余的风电转化为天然气。因此，本小节研究P2G设备及储能设备对多能耦合型微电网调度的影响。图3给出了P2G和风机出力以及储气设备的状态。

图3 P2G输出功率、风机出力以及储气设备状态Fig.3 P2G,wind power output and gas storage equipment status

由图3可知，P2G设备仅在夜间运行，因为夜间风机出力较大，同时夜间的负载需求相对较小。到了夜间，P2G设备将剩余的风电转化为天然气供气负荷使用，剩余的天然气通过储气设备储存起来，此时储气设备中的含气量逐渐变大。风机出力较低时，P2G设备的转换功率较低。随着风机出力的增加，P2G的转换功率增加，这大大促进了多能耦合型微电网对可再生能源的消纳。在利润方面，储气设备可以储存P2G设备产生的天然气，在天然气价格高的时段卖出，由此可获得更高的经济效益。

储气设备使系统能够在负荷低谷时段存储相对廉价的天然气并在天然气价格较高的时期供微电网使用，降低了系统运行成本。此外，储气设备在风电消耗和能源采购成本方面也起到了积极的作用，如表3所示。

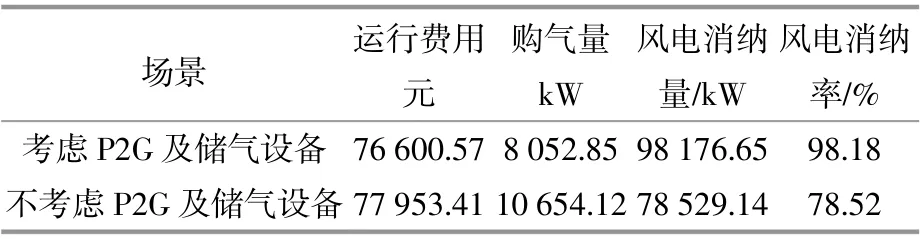
表3 P2G及储气设备对多能耦合型微电网的影响Table 3 The influence of P2G and gas storage equipment on multi-energy coupling microgrid

由表3可知，系统采用P2G及储气设备后，总成本降低了1 352.836 8元，天然气购买量减少了2 705.673 6 kW，风电消纳量增加了19 647.51 kW，风电消纳率提高了近20%。

3.2 IDR对多能耦合型微电网调度的影响

为分析IDR模型在平滑负荷曲线特性方面的性能，本文采用文献[12]定义的负荷因子、峰谷差因子、峰补偿因子3个因子来描述负荷曲线在实施IDR前后的变化。负荷因子用于评价负荷曲线的平滑度，其值为100%时，说明负荷需求全天不发生变化。峰谷差因子值越大表示峰谷差越大。峰补偿因子定义为实施基于价格的IDR后峰值负荷减少的量。

实施IDR前后，负荷特征如表4所示。

表4 实施IDR前后的负荷曲线特征Table 4 Characteristics of the load curve before and after implementing IDR

由表4可以看出，实施IDR后，电负荷的负荷因子增加了4.87%，峰谷差因子降低了7.92%。此外，峰补偿因子增长高达4.39%，天然气负荷在参与IDR后也有着同样的变化趋势。所以多能耦合型微电网在实施IDR后，负荷在高峰期有所削减，在低谷期有一定的上升，起到了很好的削峰填谷的效果。

图4，5分别为IDR对多能耦合型微电网调度的影响。由图4，5可知，本文所提出的IDR模型可以有效地平滑负荷曲线、减少峰值负荷。

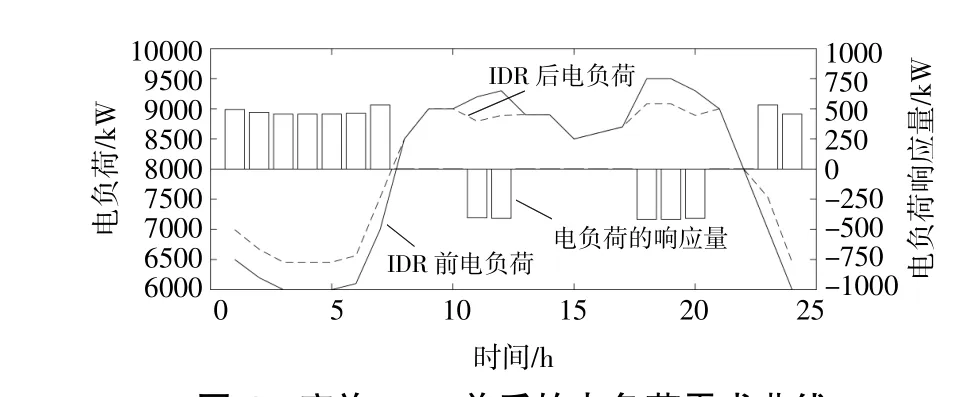
图4 实施IDR前后的电负荷需求曲线Fig.4 The electricity load demand curve before and after implementing IDR

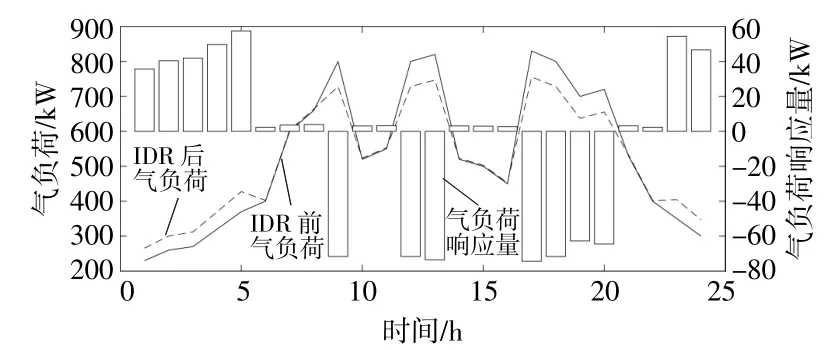
图5 实施IDR前后的天然气负荷需求曲线Fig.5 The gas load demand curve before and after implementing IDR

3.3 可信性理论的效用分析

风机出力预测值、优化值与风机出力上下限如图6所示。

图6 风机出力预测值、优化值与风机出力上下限Fig.6 The predicted value,optimized value of wind turbine output,and upper and lower limits

由图6可知，每小时最优风机出力在多数时期都高于预测值。此外，风机出力的优化值也不完全是其出力上限，这是因为较高的风电渗透水平可能会给微电网带来一定的运行风险。所提模型能够有效权衡系统运行的效益和风险。

风机出力的可信性与系统运行成本之间的关系如图7所示。

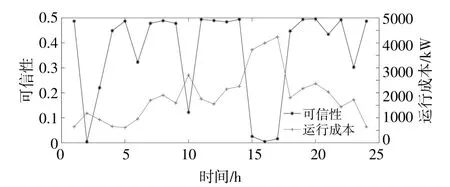
图7 可信性与运行成本的关系Fig.7 The relationship between the credibility and operation cost

由图7可以看出，二者呈负相关性。这表明较大的可信性（对应于较低的风险）对应的系统运行成本较高。所以要在两者之间进行权衡，不能一味的增大风机出力而忽略了潜在的风险。

图8对比了可信性测度、模糊和随机测度对风机出力的影响。

图8 不同测度模型下每小时风机最优出力Fig.8 The optimal hourly integrated wind power under different measures

3种测度模型对应的24 h风机出力分别为98 176.65，114 554.99，10 376.23 kW，对应的可信度分别为11.99，8.77，9.09。虽然可信性理论模型下的风机出力略小于其它两种测度模型，然而高风电渗透率对应着较低的可信度，可能给系统运行带来风险。

4 结论

为了提高多能耦合型微电网的灵活性，本文建立了计及IDR和不确定性风险的电气热耦合型微电网协同优化模型。通过对仿真结果进行分析比较，验证了本文提出模型的有效性，并得出以下结论：①本文所提模型满足了用户多样化的能源需求，降低了微电网运行成本，极大提高了多能耦合型微电网对可再生能源利用率；②将基于电价的IDR纳入到电气热耦合型微电网中，在提高负荷因子、降低峰谷差因子和提高峰值补偿因子等方面起到了积极作用。考虑IDR后，电、气负荷因子分别提高了4.87%和4.02%，峰谷因子分别降低了7.92%，7.45%，峰值补偿系数分别达到4.39%和8.96%；③通过对风电不确定性的分析，从风险规避角度看，风电渗透率高并不一定有利于多能耦合型微电网的运行。本文通过可信性理论将不确定风电视为模糊随机变量，使优化结果能够同兼顾经济性与风险水平。