计及多频率耦合特性的双馈风电-串补并网系统引发次同步振荡建模与分析

郑 絮，马覃峰

（1.贵州大学 电气工程学院，贵州 贵阳550025；2.贵州电网有限责任公司 电力调度控制中心，贵州 贵阳550002）

0 引言

受风、光自然资源的地域分布差异影响，我国新能源基地大多位于西北、华北一带，而负荷中心却位于东部或南部沿海地区，因此大规模的新能源消纳势必面临着经串补输电线路或高压直流（High Voltage Direct Current，HVDC）进行大容量、远距离外送的问题[1]。串补线路的投入及控制环节复杂的HVDC均会带来次同步振荡（Subsynchronous Oscillation，SSO）的风险[2]。近年来，国内外已经发生了多起因风电引起的SSO事故，受到国内外学者的广泛关注。随着风电装机容量的逐步增加，大规模风电场与电网间的交互作用引起的新型SSO，已成为电力系统稳定运行的一种重大挑战。

文献[3]关于风机并网过程引起次同步振荡的研究指出，感应发电机负阻尼效应是双馈风电场经串补并网引起次同步振荡的原因，转子侧变流器（Rotor-side Converter，RSC）电流内环的快速直接控制会影响系统阻尼特性。文献[4]指出了电力电子变流器与电网之间的次同步控制相互作用（Subsynchronous Control Interaction，SSCI）机理，并基于特征值分析方法初步确定了影响系统阻尼比的因素，但忽略了电流内环积分系数及功率外环参数的影响，而且并未深入地进行机理分析。文献[5]以阻抗分析方法研究了RSC的电流内环比例和积分参数对其系统等效阻抗的影响，从频域角度出发诠释了其作用机理。文献[6]进一步探讨了RSC功率外环参数的影响，指出了功率外环对次同步振荡的影响不可忽略。文献[8]采用传统的复转矩作用系数法，从定转子电磁转矩与转速的关系方面解释了变流器控制参数对次同步振荡稳定性的影响。目前，针对双馈风电场并网引起的次同步振荡的研究较多，但对其机理特性还未有统一的结论，尤其是涉及多频率耦合特性的次同步控制相互作用机理的文献较少。现有文献大多都只关注双馈风电场在某一次同步频率下的振荡机理及抑制措施研究，然而在实际运行系统中却经常发生具有多频率耦合特性的次同步振荡。

本文以双馈风机经串补并网系统引发次同步振荡为研究对象，建立了双馈风机串补并网后的等值系统模型；研究具有多频率耦合特性的SSCI引起次同步振荡的机理；通过时域仿真法对其多频率耦合特性进行验证。本文还分析了串补度、风速、并网台数等系统运行参数及非线性环节对次同步振荡控制的影响，进一步研究了不同因素引发次同步振荡的机理。通过对双馈风电场经串补并网引起的新型次同步振荡特点的分析，实现对并网系统的稳定控制。

1 双馈感应电机并网系统及其运行原理

1.1 双馈感应电机并网系统介绍

本文主要针对风机、变流器与电网间的交互原理进行研究，在进行建模时采用单机等值模型，忽略各风电机组运行参数和地理位置的差异性。假设风电场内各风机的运行工况相近，可通过搭建详细的单机风电并网电磁暂态模型对其进行等值，在保证模型结论可靠的前提下大大降低了复杂风电场建模的难度[9]，[10]。等效后的双馈并网等值模型如图1所示。

图1 双馈风电场并网系统等值模型Fig.1 Equivalent model of grid-connected system of doubly-fed wind farm

风电场中的双馈感应发电机（DFIG）主要包括风力机、机械传动链（齿轮箱，传动轴）、绕线式感应电机、变流器（RSC，GSC）和控制系统5部分。图1中：Te为发电机电磁转矩；ωr为双馈风机转子角速度；GSC为网侧变流器；is，ir，ic分别为双馈风机定子电流、转子电流和GSC输出电流；T1为风机箱变；T2，T3为线路升压变压器；RL，XL，XC分别为输电线路折算到500 kV侧的等效电阻、电感和串补电容。

1.2 控制系统

DFIG控制系统主要包括变速风力机的控制系统、RSC控制和GSC控制3部分。

图2为变速风力机控制系统，其控制对象为风轮叶片桨距角和发电机的电磁转矩。当实际风速低于额定风速时，控制系统将叶片桨距角调为0 °，并调整电磁转矩以控制发电机的转速，使其实现最大功率追踪。当风速高于额定风速时，控制系统将增大叶片桨距角β，从而减少风能的吸收，使其限制在额定功率下运行。

图2 变速风力机控制系统Fig.2 Variable-speed wind turbine mechanical control system

RSC采用基于定子电压定向的矢量控制方式，通过控制转子dq轴电流来控制有功和无功功率输出，含有功率外环和电流内环，实现有功、无功的近似解耦。GSC控制逻辑与RSC类似，主要维持直流母线电压和维持机端电压恒定，含有直流电压外环和电流内环。图3为典型双馈风机的RSC，GSC控制框图。

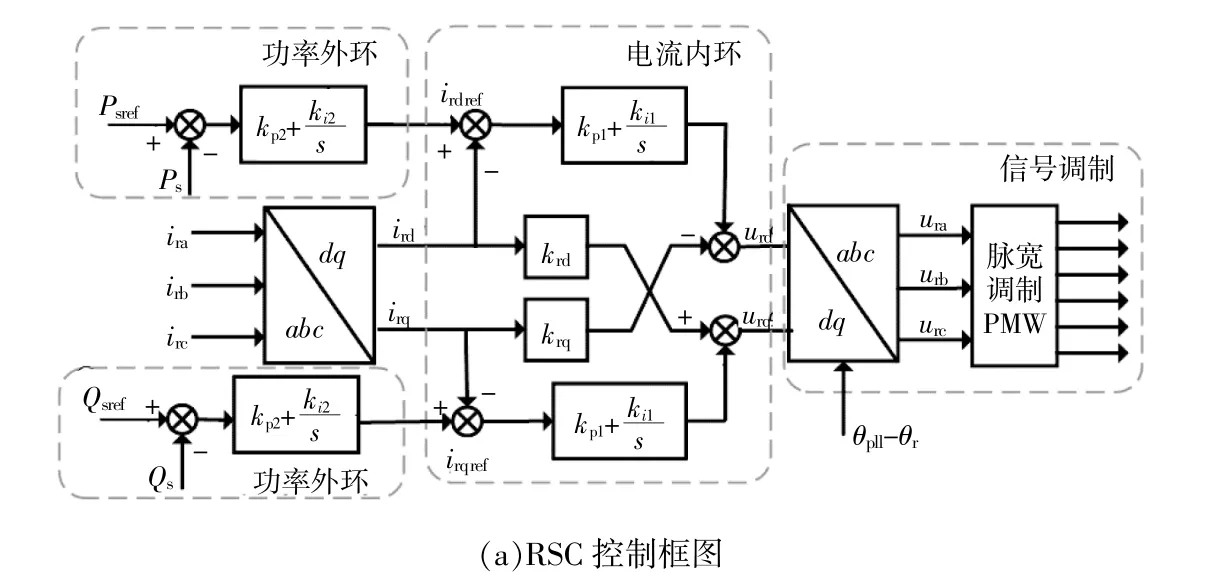
图3 典型双馈风机RSC，GSC控制框图Fig.3 RSC，GSC control block diagram of a typical DFIG

2 双馈感应电机并网次同步振荡的机理分析

双馈风机经串补并网引起次同步振荡的机理：一是传统感应电机的负阻尼效应，二是具有多频率耦合特性的次同步控制相互作用。随着风电并网容量的增加，电网呈现较为薄弱的网特性。当电网阻抗增大时，控制器中锁相环和直流电压环与电网阻抗之间的交互影响加深，谐振频率趋于低频段，加剧了系统频率之间的耦合，导致系统不稳定。部分不对称谐振的出现取决于电网阻抗的强度，短路比越低，越容易出现不对称谐振。在弱电网条件下，不对称谐振引起的频率耦合特性会危害系统的稳定性。变流器直流侧与交流侧之间的不对称关系，也使变流器主电路存在频率耦合特性。目前，在变流器建模过程中，综合考虑锁相环和电压环对频率耦合分量影响的研究还有所不足。

2.1 负阻尼效应

由于双馈风机为绕线式的感应电机，其等效电路如图4所示。

图4 双馈风机等效电路图Fig.4 Equivalent circuit diagram of DFIG

当DFIG定子绕组中含有次同步频率分量时，在此次同步频率fer下的转差率S=（fer-fr）/fer。由于fer＜fr，故转差率S＜0，则在转子绕组侧Rr/S＜0。当转差率幅值的绝对值超过电枢的电阻时，此时DFIG具有负电阻，则在转子绕组侧Rr/s＜0。当转差率幅值的绝对值超过电枢的电阻时，此时DFIG具有负电阻。DFIG接入系统后便给整个风电并网系统引入了负阻尼，可能引起自激，进而导致定子电流持续增加或振荡。

2.2 多频率耦合特性的SSCI数学机理分析

在DFIG稳态运行时，转子转速频率为fr。由双馈风机变速恒频发电原理可得，转子绕组三相电流的频率为f0-fr（f0为旋转磁场切割定子绕组的频率，稳态下为50 Hz）。假定在某一时刻网侧发生小扰动，产生一个频率为fer次同步扰动电流时，由于DFIG定转子磁链耦合作用，在转子绕组三相电流上必然感应到一个频率为fer-fr的扰动分量。即：

此时，同步旋转坐标系下转子电流中，只包含稳态分量Ird0，Irq0以及与定子磁链耦合作用产生的ΔIrd，ΔIrq。考虑到RSC功率外环与风力机输出的机械转矩有关，其控制时间尺度比电流内环控制时间尺度更大（外环为s级，而电流内环为ms级），在分析时认为转子电流内环参考值不变。当受扰后转子dq轴电流ird1，irq1经过图3所示的RSC电流内环控制后，输出的转子电压调制信号urd，urq也会产生相应的扰动量。

由式（5）可以看出，在未考虑次同步扰动分量对锁相环输出的影响时，当电网侧产生次同步频率fer的扰动，静止坐标系下转子三相电压中除了自身含有f0-fr转子基频分量外，还耦合出频率为（fer-fr）和（2f0-fr-fer）的次同步扰动分量。然而，在双馈风机并网系统中，由于RSC以及GSC电流内环的输入与输出调制信号均有PLL参与，其PLL的动态特性将会直接影响到输出电压指令值，故须要进一步研究次同步扰动量对PLL输出的影响。本文采用一阶PLL，其结构框图如图5所示。

图5 PLL结构框图Fig.5 PLL structure block diagram

当网侧中存在次同步频率为fer的扰动时，PLL的输出相角会产生一个偏差Δθ。此时PLL的锁相误差y如图6所示。

图6 存在扰动时PLL坐标示意图Fig.6 Schematic diagram of PLL coordinates when there is disturbance

图6中：θpll0为稳态时锁相环输出的相角；θpll为网侧存在扰动时锁相环输出的相角；Δθ为锁相环的误差，当网侧不存在扰动时，Δθ=0。

由图5，6可以看出，考虑锁相环输出相角误差时，受扰后dq坐标系下的变量y2与原来稳态时dq坐标系下的变量y1关系为

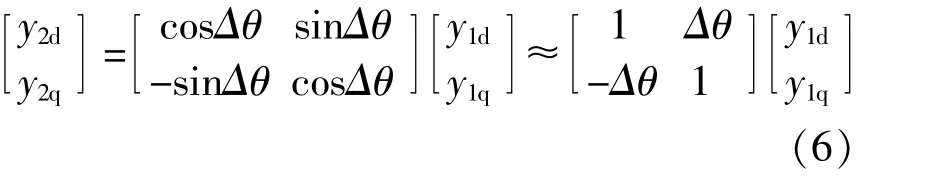
式中：Ard0，Arq0分别为未发生扰动时电压幅值的d，q轴分量；Ard1，Arq1分别为频率为f1-ff的电 压分量幅值的dq轴分量；Ard2，Arq2分别为频率为2（f1-ff）的电压分量幅值的d，q轴分量。

综上可见，可以得到双馈风机并网次同步振荡的多频率耦合过程。在三相静止坐标系下网侧定子电压、电流中出现次同步扰动量fer时，经过park变换同步旋转坐标系下定子电压、电流，会产生f0-fer的扰动分量。由于风机定转子磁链耦合作用，导致三相转子电压、电流产生fer-fr的扰动分量，进而同步旋转坐标系下DFIG转子电压、电流中也会含有f0-fer的扰动分量。当定转子同步旋转坐标系下频率为f0-fer的扰动量经过其变流器控制回路，会使得DFIG三相定子电压、电流中耦合出频率为fer的次同步分量以及2f0-fer的超同步分量。当考虑锁相环输出相角扰动时，同步旋转坐标系下的DFIG转子电压、电流耦合出n（f0-fer）（n=1，2，…）的倍频分量。当其继续作用于变流器控制回路时，DFIG三相定子电压、电流中会耦合出n（f0-fer）±f0的分量。

当耦合出来新的频率分量和原始扰动分量相互叠加，使得原始次同步扰动助增。新的次同步扰动再经双馈风机、控制回路以及PLL形成正向反馈激励，加剧了整个系统的负阻尼程度，导致整个DFIG并网系统输出的有功和无功功率振荡发散，引起次同步振荡。

3 多频率耦合特性分析

为了进一步研究风电场频率耦合特性，验证上述推导的正确性，在PSCAD/EMTDC上搭建了图1所示的双馈风电场并网系统的电磁暂态模型。风电机组以及线路相关参数列于表1。

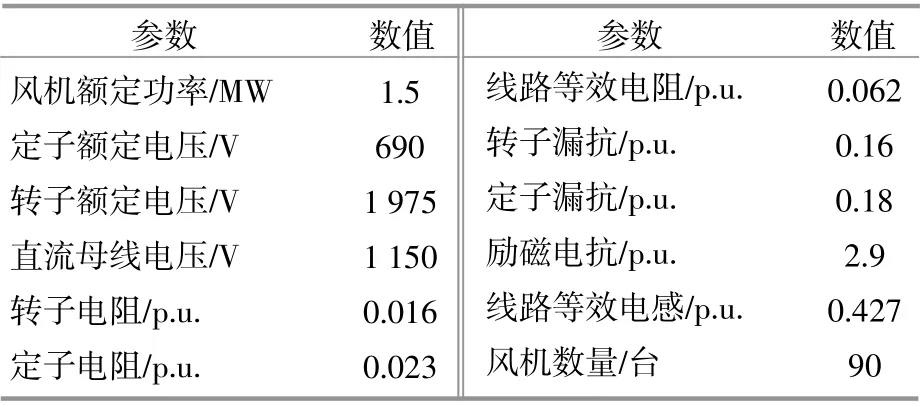
表1 双馈风电机组和输电线路参数Table 1 Parameters of doubly-fed wind turbines andtransmission lines

系统稳态时，风电场输出的有功功率为135 MW，无功功率为0。设置t=5 s时，投入线路串补电容，串补度为60%，以模拟系统网侧发生次同步扰动。随后，系统发生了频率约为27.8 Hz的次同步振荡，其中DFIG的定、转子电流a相波形如图7所示。

图7 静止坐标系下定、转子a相电流波形Fig.7 The stator and rotor a-phase current waveforms in the stationary coordinate system

当系统投入串补电容后，定、转子电流波形发生了较大的畸变。定、转子电流频谱分析结果如图8所示，稳态转差频率分量为8.8 Hz（fr-f0），其幅值最高，此时fr=58.8 Hz。除此以外，转子a相电流还含有31 Hz（fr-fer），13.4 Hz（2 f0-fr-fer）分量。定子a相电流除了含有50 Hz工频分量外，还含有幅值较高的27.8 Hz的次同步分量（fr），72.2 Hz的超同步分量（2 f0-fer），16.6 Hz（2f0-3fer）。其余频率分量的幅值较小，不再给出。

图8 静止坐标下定、转子a相电流FFT频谱分析结果Fig.8 FFT spectrum analysis results of stator and rotor a-phase current in static coordinates

同步旋转坐标系下，定、转子的d轴电流波形及频谱分析结果如图9，10所示。由图9，10可知，同步旋转坐标系下定子电流除了直流分量外，还含有次同步频率互补分量22.2 Hz（f0-fer），44.4 Hz（2 f0-2 fer）和66.6 Hz（3 f0-3 fer）倍频分量。这些频率分量符合多频率耦合特性的规律。

图9 同步旋转坐标系下定、转子d轴电流波形Fig.9 Current waveform of stator and rotor d-axis in synchronous rotating coordinate system

图10 同步旋转坐标下定子d轴电流FFT频谱分析结果Fig.10 FFT spectrum analysis results of stator d-axis current under synchronous rotating coordinates

4 次同步振荡分析

为了揭示双馈风电场并网引起SSO的机理，探究不同因素下负阻尼效应和SSCI作用的影响程度。在搭建的双馈风电场并网电磁暂态模型的基础上，进一步研究风电场的系统运行参数、变流器控制参数和限幅环节等因素对系统次同步振荡的影响，并结合多频率耦合特性对风电场次同步振荡主导因素进行深入分析。

4.1 系统运行参数的影响

首先研究对双馈风电场影响较大的线路串补度。根据实际系统，两条500 kV线路的串补度为20%，设置风机并网台数为90台，并网容量为135 MW，风速为15 m/s，依次改变线路串补度，仿真结果如图11所示。由图11可知，5 s时投入电容，随着线路串补度的增大，系统阻尼降低，稳定性变差，风电场输出的有功由稳定变为发散。由局部放大图可见，随着串补度的增加，系统振荡频率也逐渐降低。由于系统固有谐振频率降低，导致转差绝对值进一步减小，（s=1-f0/fer），从而导致负阻尼进一步增大（Rr/s）。此时，感应电机的负阻尼效应为引起系统次同步振荡的主导因素。

图11 不同串补度下风电场输出的有功功率Fig.11 Active power output by wind farms under different series compensation degrees

研究风电场的并网容量对系统次同步振荡的影响。设置风速恒定为15 m/s，改变并网台数为6～90台，其余控制参数不变，仿真结果如图12所示。

图12 不同并网台数下风电场输出功率Fig.12 Wind farm output power under different numbers of grid-connected units

由图12可知，在并网容量逐渐增大的过程中，风电场输出功率先发散后收敛，系统的稳定性先变差后增强，即在某一特定的风速下，存在某一并网容量使得其系统阻尼特性最差。这是因为随着并网容量的增加,风机的并网台数也增大，整个系统的等值电路参数会发生变化，从而导致系统层面的串补度发生变化，进而影响系统的阻尼特性。

4.2 变流器控制参数的影响

已有研究表明，GSC控制参数对风电场并网系统阻尼影响较小，可忽略不计[11]。本文只对RSC电流内外环和功率外环参数进行分析。仿真条件同4.1节。依次改变控制器比例Ke、积分系数Kr，仿真结果如图13～16所示。其中，RSC电流内环比例参数、积分参数，RSC功率外环比例参数、积分参数分别为Kp1，Ki1，Kp2，Ki2。

图13 不同RSC电流内环比例参数下风电场输出功率Fig.13 Wind farm output power under different RSC current inner loop ratio parameters

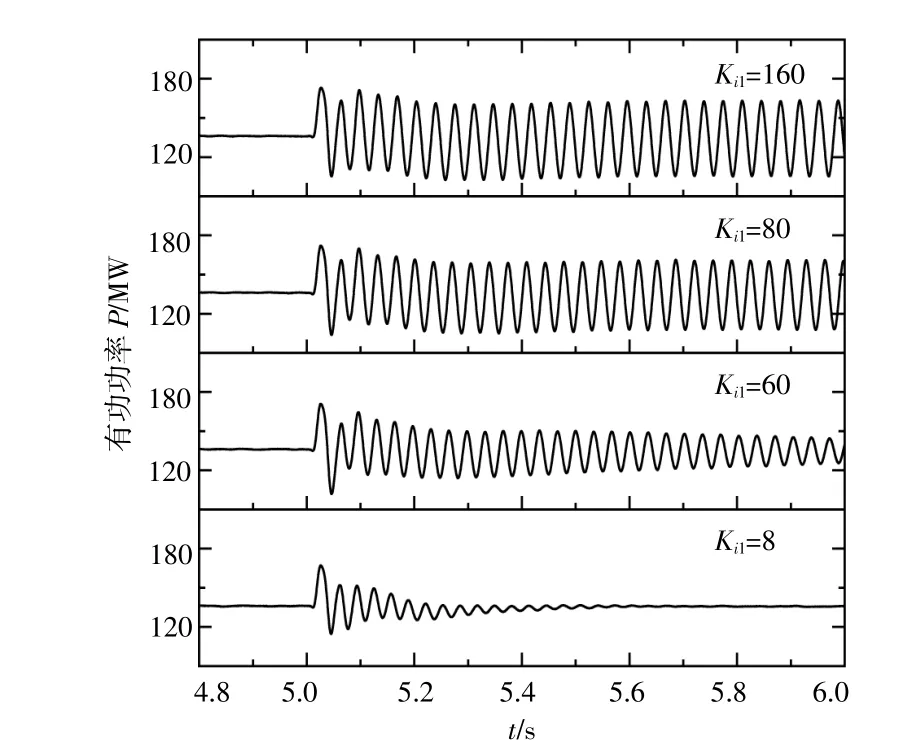
图14 不同RSC电流内环积分参数下风电场输出功率Fig.14 Wind farm output power under different RSC current inner loop integral parameters

图15 不同RSC功率外环比例参数下风电场输出功率Fig.15 Wind farm output power under different RSC power outer loop ratio parameters

图16 不同RSC功率外环积分参数下风电场输出功率Fig.16 Wind farm output power under different RSC power outer loop integral parameters

由仿真结果可知，当改变RSC与GSC电流内环的比例积分系数时，系统阻尼均会发生变化，且随着系数Kp，Ki的增大，系统由稳定变为不稳定，风电场输出的有功由稳定变为发散。此外，通过观察不同系数变化程度对风电场输出有功功率曲线的影响可见，控制器比例系数Kp均比积分系数Ki影响程度大；按影响程度大小依次为转子侧电流内环比例系数、功率外环比例系数、电流内环积分系数和功率外环积分系数。

为了进一步探究控制器参数引起的次同步振荡的原因，选取了对系统阻尼影响最大的RSC电流内环比例参数，对不同比例参数下的定子电流及定子d轴电流分量进行频谱分析。由于篇幅所限，此处不再给出频谱分析图，仅给出频谱分析结果（表2）。

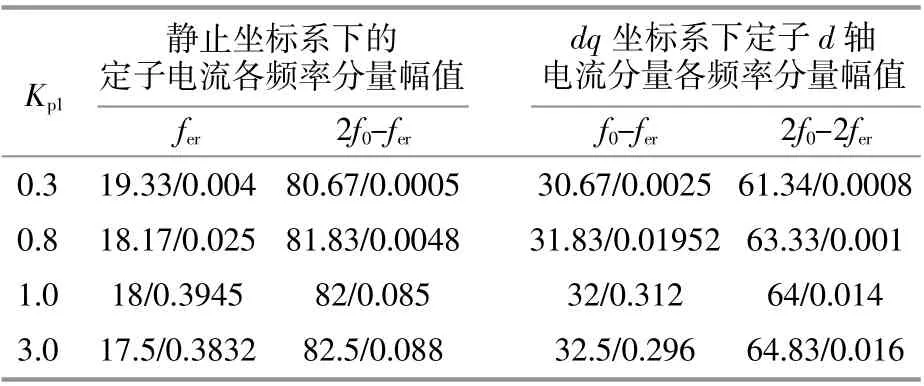
表2 双馈风机电流内环不同比例参数下的频率响应Table 2 Frequency response of doubly-fed wind turbine current inner loop with different proportional parameters

由表2可以看出，当电流内环比例参数Kp1变化10倍时，次同步振荡频率fer由19.33 Hz到17.5 Hz，其谐振频率变化仅不到2Hz。此时由变流器控制回路耦合作用产生的次同步分量fer幅值增大了将近100倍；定子电流中次同步谐振分量fer幅值占基波的比例由0.4%变为39.4%，d轴定子电流分量f0-fer幅值占直流分量的比例由0.25%变为31%。这说明当系统串补度恒定时，其谐振频率基本不变，随着Kp1的增大，系统控制回路耦合作用产生的各频率分量幅值均增大，这进一步加剧了系统的负阻尼程度。此时，具有多频率耦合特性的SSCI为引起次同步振荡的主导因素。

4.3 限幅环节的影响

由于电力电子器件具有容量限制且易过流的特点，因此在系统控制回路中为了保护变流器的开关器件而引入了多个信号限幅环节。这给系统运行引入了非线性特征，有可能影响系统的阻尼特性，进而导致振荡的产生[12]。为了更全面地揭示双馈风电场并网引起次同步振荡的影响因素，本文进一步研究了限幅环节对系统稳定性的影响。

本文所搭建的双馈风机控制系统的主要限幅环节包括RSC功率外环限幅、电流内环参考值限幅及电流内环PI调节器的输出、GSC直流母线电压限幅和电流内环PI调节输出限幅等。考虑所提出的RSC电流内环比例参数对系统稳定性的影响较大，故本文限幅部分着重考虑电流内环PI调节器限幅值对系统次同步振荡的影响。

将电流内环比例系数Kp1设为1，依次提高限幅的上下限，RSC电流内环PI调节器dq轴输出信号和风电场输出功率的波形如图17所示。

图17 不同限幅值的风电场输出功率Fig.17 Wind farm output power under different limiting values

由图17可知，有限幅环节时，影响了振荡的幅值，但振荡频率基本不变。当限幅为0.1 p.u.时，RSC电流内环d轴输出信号在5.06 s即进入等幅持续振荡状态。当增大限幅值为0.15 p.u.时，输出信号在5.22 s进入等幅持续振荡状态。当取消限幅时，输出信号则逐步由振荡发散到形成持续稳定的振荡，并且限幅环节通过影响输出的dq轴信号而影响风电场输出的有功。

限幅环节不是产生持续振荡的原因，而是对原有次同步扰动分量幅值进行了钳位，被动地参与了振荡。与此同时，观察了RSC以及GSC中的其他限幅环节，发现其输出信号均未达到限幅值。由此也可看出，RSC电流内环PI调节器的限幅环节是使系统次同步振荡进入等幅持续振荡阶段的主要原因，并且限幅值越小，进入等幅持续振荡阶段的时间就越短。通过多频率耦合振荡与仅考虑单一频率振荡的仿真对比结果可以看出，多频率耦合振荡更加接近实际情况（图18）。

图18 单一频率多频率耦合振荡对比分析Fig.18 Comparison and analysis of single-frequency and multi-frequency coupling oscillations

5 结论

本文基于某实际风电场运行数据建立了双馈风电场经串补并网的简化等值模型。为了全面揭示双馈风电场并网引发次同步振荡的机理及特性，基于DFIG控制回路定性推导了SSCI多频率耦合过程；基于时域仿真模型对双馈风电场经串补并网的简化等值模型进行验证，进一步探讨了双馈风电场并网引起次同步振荡的影响因素。

在控制参数一定时，风电场的系统运行参数线路串补度和风速，通过影响系统的固有谐振频率引起负阻尼效应。串补度越高、风速越低，系统的阻尼越差，越容易引起次同步振荡。

当系统运行参数一定时，通过变流器控制回路参数的改变，来影响SSCI多频率耦合过程，加剧系统负阻尼。RSC电流内环比例参数对系统阻尼的影响最大，其值越大，越容易引起次同步振荡。