Hartree方程的低正则算法

李雪,李新彤

(天津大学 应用数学中心,天津 300072)

在这篇文章中,考虑Hartree方程：

(1)

其中Td=(0,2π)d,u=u(t,x):R+×Td→C,u0∈Hγ(Td)(γ≥0)为给定的初值.非线性Hartree方程在量子理论中有非常广泛的应用,它描述了量子力学中多玻色子系统场方程的经典极限[1].因此自提出以来就备受研究者关注,并已经有了大量理论研究成果[2-3]和数值求解方法,包括有限元方法[4-5]、有限差分方法[6-7]和分割法[8-9]等.

上述数值方法都是基于精确解足够光滑的假设构造的,特别地,经典的Strang Splitting方法要求u0∈Hγ+2才能获得相应的数值解和真解之间的一阶收敛[10],即一阶精度需有两个导数损失.本文的目标是通过构造一类新的算法,使其一阶精度所要求的初值正则性更低.本文的算法构造基于指数型积分算法[8].相应的非线性Schrödinger方程的相关研究可见文献[11-13]及其参考文献.

定义函数φ如

并定义泛函

给出如下算法,

(2)

其中un为u在t=nτ时的数值解.主要的定理为:

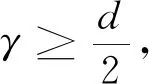
在定理1中,可得到一阶收敛性仅需损失一个导数,因此改进了Strang Splitting等方法获得的结果.

1 预备知识

下面提供一些有用的定义和性质.

使用AB或者BA来表示A≤CB,对于某些绝对常数C>0.使用A～B来表示ABA.

定义〈·,·〉为L2内积,

(3)

函数f在Td上的Fourier变换定义为

(4)

Fourier逆变换为

(5)

Fourier变换常用性质

(6)

(7)

Sobolev空间Hγ(Td),γ≥0的范数

(8)

定义算子Js为

(9)

(10)

文中,将经常应用下面的Kato-Ponce不等式(简单版本),这最初是由文献[14]证明的,最近在端点处[15]取得了重要进展.

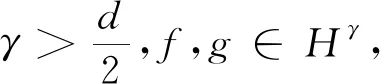
‖Jγ(fg)‖L2‖f‖Hγ‖g‖Hγ.

(11)

2 收敛性分析

根据Duhamel公式,满足方程的解(1)有如下等式

对上式做Fourier变换可得,

(12)

进一步可得

(13)

令τ=tn+1-tn,并且记φ=|k|+|k1|-|k2|-|k3|=2|k1|2+2k1k2+2k2k3+2k3k1=α+β,其中α=2|k1|2,β=2k1k2+2k2k3+2k3k1.于是有

(14)

将(14)式带入(13)式,整理可得:

(15)

其中,

对(15)式逆Fourier变换得

3 定理1的证明

3.1 关于和的估计

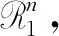
(16)

证明

(17)

其中

只需计算其中一个估计,其他类似可得.

Cτ[‖||γ-d+1|e-isΔv(tn)|2‖L2·‖eisΔ(v(s)-v(tn))‖L∞+

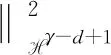
(18)

其中,有

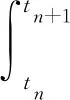
于是

因此,(18)式可以写为

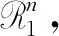
(19)

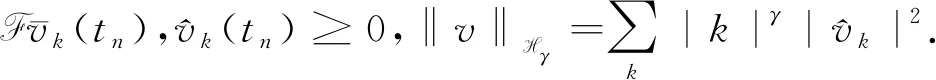
上式逆傅立叶变换得

于是有

(20)

3.2 定理1的证明

接下来证明定理1.

证明

vn+1-v(tn+1)=Φ(vn)-v(tn+1)=Φ(vn)-Φ(v(tn))+Φ(v(tn))-v(tn+1)=

(21)

根据引理2和引理3得如下误差估计

(22)

记en=v(tn)-vn,利用Kato-Ponce不等式可得稳定性估计

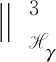
由此,定理1得证.