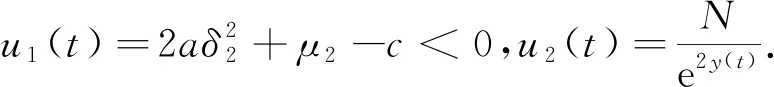污染环境影响的流行病模型动力学行为研究

朝治琴，张启敏

(宁夏大学 数学统计学院，银川 750021)

近年来，极端气候天气的频繁发生和工业废弃物的排放[1]对生态环境质量产生了极大的影响，这些因素也加重了患呼吸道疾病的风险[2]，因此引起了生态、医疗、数学等相关领域学者的极大关注.例如BAKONYI等[3]研究了空气中的钒、碳元素或可吸入颗粒与呼吸系统疾病恶化之间的相关性.LI等[4]构建了综合模糊模型研究了空气污染对哮喘易感的影响.魏妮等[5]讨论了大气中污染物浓度对儿童常见呼吸道疾病的影响.周历媛[6]给出了空气污染物浓度越高，呼吸道疾病患者分布越密集，并阐述了随着空气污染物浓度的不断增加，呼吸道疾病患者也会越来越多.此外也有实验和研究表明室外空气污染的严重程度可以导致呼吸道等病毒感染的风险增加[7-9].

以上学者主要研究了大气污染与呼吸道疾病的相关性，但未考虑如何设计控制策略来降低污染物浓度的变化和随机噪声对流行病的影响.事实上温度、湿度、沙尘等随机现象的经常发生都会影响空气质量[10]，所以为了客观、全面地了解呼吸道疾病性态，应考虑这些因素对其产生的影响.另一方面控制污染物的排放是预防大气污染的有效途径[11]，而对呼吸道疾病的治疗则是控制疾病传播的重要手段[12].因此在模型中加入了控制因素对大气污染和疾病的干预.本文建立了污染环境中的流行病模型，研究空气污染的变化和随机噪声对呼吸道疾病的动力学行为.

1 模型建立

研究空气污染和随机干扰下呼吸道疾病动力学时，通常采用SIS模型的建模方法.其中S是易感染个体数量，I是传染个体数量.假设总人口数为N，则易感个体的数量可以表示为N-I.呼吸道疾病传播率函数用β(t)表示，空气质量指数用F(t)的函数表示.假定疾病的传播率依赖于空气污染水平，用β(F(t))表示，这是易感者与受感染个体发生潜在传染性接触的速率，它会随F(t)值不断变化.因此进一步假定这种关系是线性的，即β(F(t))=βF(t).用μ(t)表示空气清除率，假定污染物的流入速率为常数c.在模型中，由于β(t)以及μ(t)都会受到随机扰动的影响，因此将βF(t)和μ(t)分别用β(F(t))+δ1η1和μ(t)+δ2η2来表示，其中η1和η2代表白噪声，δ1和δ2分别代表白噪声η1和η2的强度.此外，用u1(t)表示控制污染物排放，用u2(t)表示人为对疾病的干预，例如治疗、隔离、媒体宣传、防护等.根据以上分析，可以得到各因素之间的关系，如图1所示.

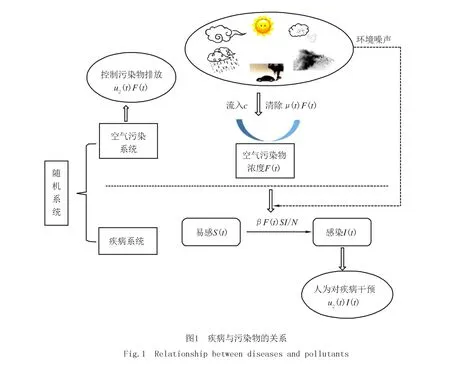
通过图1，在文献[13]的基础上考虑控制向量，得到下列污染环境中的流行病模型：

(1)

这里的B1(t)和B2(t)是独立的标准布朗运动.其中模型中所涉及的常数N，β，C，δ1，δ2均大于零.

2 有界性与稳定性

对于模型(1)，需进一步研究污染物浓度的有界性和疾病传播的动力学性质.由于(1)式中的两个方程是耦合的，首先分析F(t)的性质.在下列分析中，令μ1≤μ(t)≤μ2.

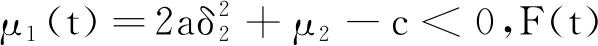
(2)

其中K(p)是依赖于p的常数，与初始值F0无关，即F(t)的p阶矩有界.

证明定义V(F(t))=F(t)p，对F(t)∈R+，0

在区间[0,t]上对两边同时积分并取期望

可以得到

(3)

根据μ1≤μ(t)≤μ2，(3)式可以写为

(4)

再令x(t)=E(Fp(t))，可以得到

(5)

对于0

(6)

由方程解的性质可以得到

令

则

所以方程(6)的解为

(7)

定理1给出了系统的有界性，基于这一性质，下面给出系统稳定的条件.

证明取I0∈(0,N)，那么对于所有的I>0，I(t)∈(0,N)成立.只需要对上述定理在区域Γ上给一个证明，这里的Γ={I∶0

(8)

此外

(9)

定义一个C2上的函数V∶[0,∞)×R+→R

(10)

其中k(t)是方程

(11)

的正数解.

直接计算可以得到

(12)

(13)

将(11)式代入(12)式可以得到

(14)

(15)

(16)

对于(16)式，当r→∞时，有

(17)

即上述定理得证.

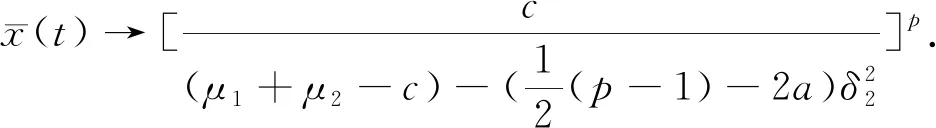
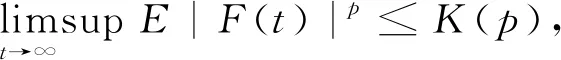
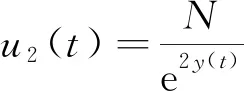
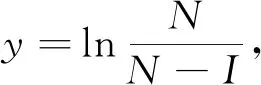
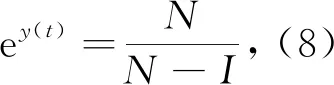
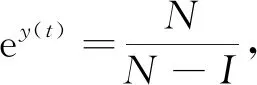
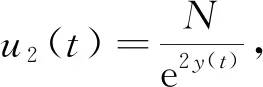
3 总 结