基于多种群的粒子群优化算法
杨 娜, 刘爱华, 易 堃, 占 凯, 王阳阳
(上海无线电设备研究所,上海 201109)
0 引言
弱目标检测时通常采用长时间积累,通过增加目标照射时间的方式提高目标回波的信噪比,从而提高雷达检测性能。由于目标的高速机动,在雷达的长时间回波积累过程中,目标回波信号分布跨越距离和频率分辨单元而造成能量发散。长时间相参积累是一种基于“检测前聚焦”的相参积累技术,它能够获得良好的目标检测性能,从而提高雷达对隐身目标的作用距离。基于长时间积累的粒子群优化(particle swarm optimization,PSO)算法采用一种新的搜索、匹配和积累的方法,在检测时刻实现距离和速度参数“聚焦”而形成一个能量峰,利用回波能量聚集提高对高机动高速隐身目标的检测及跟踪能力。文献[1]针对雷达动目标提出了基于拉东-分数阶傅里叶变换(Radon-FRFT)的长时间相参积累检测算法,但该方法需要遍历所有搜索参数,计算量大且效率较低,不能满足弹载雷达实时性应用需求。文献[2]针对卫星目标提出了利用运动特性进行包络补偿和相位补偿的方法,但是该方法只适用于船载雷达跟踪空间目标,并不适用于弹载雷达对隐身目标的跟踪。文献[3]提出基于粒子群优化算法的位置搜索方法,利用遗传学的相关知识进行选择优化,但是未考虑基于粒子群优化算法的搜索方法可能陷入局部收敛,在信噪比较小的情况下并不适用。文献[4]研究了传统PSO算法原理,该算法主要是单种群寻优,很容易陷入局部最大值,导致搜索停止。为解决粒子紧密聚集的难题,避免传统单种群PSO算法可能导致的种群局部收敛,可以在粒子群搜索时增加种群数量。本文提出基于多种群的PSO算法,采用双种群寻找最优值,通过局部最优和全局最优对比,提升粒子群对最优值的搜索动力,避免过早停滞,在保证精度和实时性的前提下完成信号检测。
1 传统PSO算法
传统PSO算法主要通过粒子之间的集体相互合作使整个种群逐渐进化,每个粒子都根据种群以前的最优值及该粒子曾经的最好值逐步调整移动轨迹,最终使每个粒子收敛到种群最优值。把寻优过程当作是鸟群在空中捕食,粒子群优化算法在解空间中的粒子值看成飞行中的一只鸟,寻找的最优值就是食物。粒子的位置代表粒子的个体值,粒子的更新值代表鸟群的飞行距离及方向。PSO算法是对鸟群觅食的模拟,通过粒子间信息互相交换,从而影响整个种群的飞行方向。鸟依据自己及同伴的经验来调整飞行,依靠鸟群间的信息共享使整个鸟群达到最优值。各个粒子在飞行时找到的最优值,即该粒子最优值;种群飞行所经历过的最优值,即种群最优值。
粒子群优化算法首先将长时间积累的雷达回波数据进行分段,得到多段可相参积累的短时间回波数据,使得每段内目标不会跨距离单元和频率单元,并对每段脉冲数据进行快速傅里叶变换(FFT)处理;再利用PSO算法搜索粒子的距离、速度、加速度等参量,迭代寻找全局最优粒子,作为目标的距离、速度和加速度估计参数。
传统的粒子群优化算法采用固定权值种群,由于速度权值系数不变,粒子更新值固定,粒子搜索的空间相对稳定,可能产生早熟或停滞现象。设()表示第次迭代时的粒子个体更新值,()表示第次迭代时的粒子个体值,()表示第次迭代时的粒子最优值,为粒子群最优值,则粒子个体更新值及更新方程为
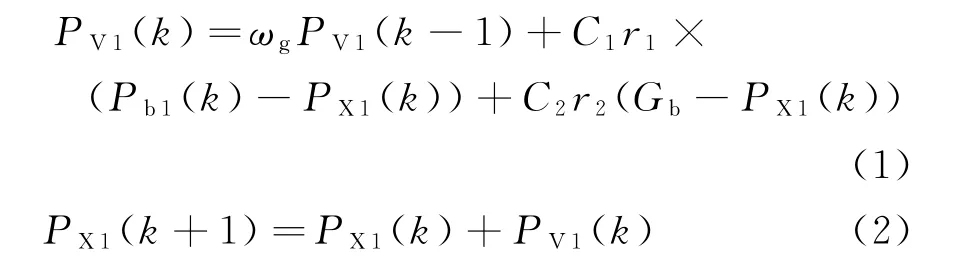
式中:为固定速度权值系数,通常取0.5;为个体最优值对粒子更新的影响系数,通常取1.8;为群体最优值对粒子更新的影响系数,通常取1.8;和为0~1的随机数。
2 多种群PSO算法
多种群PSO算法在传统PSO算法的基础上增加变权值种群,采用两个种群寻找最优值,并用速度权值系数来控制粒子以前速度对当前速度的影响。种群1为固定速度权值种群,速度权值较大且固定不变,则粒子更新值较大,有利于粒子搜索更大的空间,可能发现新的解域,全局搜索能力较强。种群2为变速度权值种群,通过改变速度权值的大小控制种群搜索的范围,先进行全局大范围搜索最优值,然后局部寻优。速度权值越大,种群的全局寻优能力越强;速度权值越小,种群的局部寻优能力越强。在应用时,随着迭代次数的递增,速度权值由初值0.8减小为0.1,这样就可以达到先全局搜索后局部搜索的效果。变权值种群粒子个体更新值及更新方程为
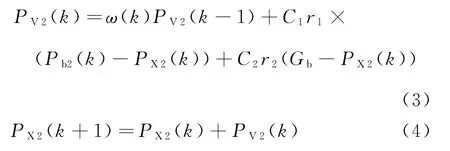
式中:()为第次迭代时的速度权值;()为第次迭代时种群2的粒子个体更新值;()为第次迭代时种群2的粒子个体值;()为第次迭代时种群2的粒子最优值。()的更新方程为
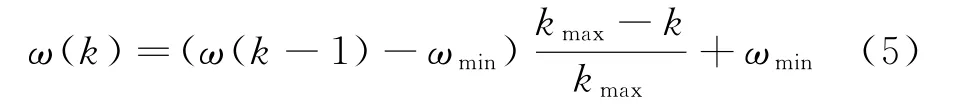
式中:为最小权值,通常取0.1;为最大迭代次数,通常取200。
3 仿真对比分析
结合实例仿真分析多种群PSO算法,用Matlab软件生成回波数据。设弹目距离500 m,弹目相对速度300 m/s,弹目相对加速度50 m/s。初始化雷达参数,脉冲重复周期8.5μs,采样率4 MHz,距离门数34,积累脉冲数16 384,即长时间积累139.264 ms数据。
长时间积累时,目标回波跨单元会导致积累检测性能下降。首先将回波数据进行分段,使得每段内目标回波不会跨频率单元和距离单元,再对分段回波数据进行FFT。分段是指在频率维将长时间积累脉冲分成多段短脉冲,长脉冲分段方法如图1所示。长时间积累回波包含16 384个脉冲,积累时间为139.264 ms,把长脉冲分成32段,分段后的脉冲数为每段512个,每段的积累时间为4.352 ms。分段后每段距离为1.306 1 m,小于距离分辨率37.5 m;每段速度为0.217 6 m/s,小于速度分辨率2.056 5 m/s,能保证分段后的每一段回波数据不会跨频率单元和距离单元,以便进行相参积累。初始化所有粒子的距离范围(0~1 275)m、速度范围(200~400)m/s、加速度范围(-100~+100)m/s、固定权值种群1粒子个数128、变权值种群2粒子个数128、两种群交换长度40。
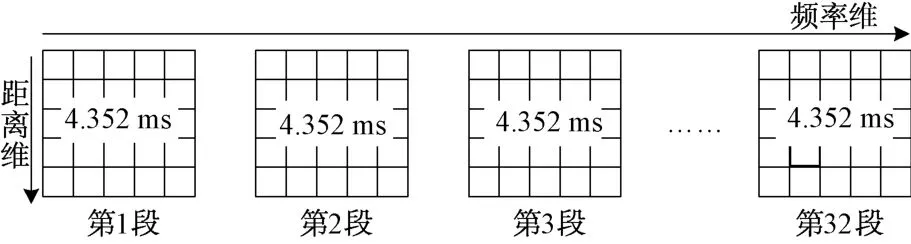
图1 长脉冲分段示意图
粒子适应度的计算方法是每段回波数据进行FFT,对粒子所在位置进行相位补偿后相加再取模。根据粒子的距离、速度和加速度计算距离走动量和速度走动量,确定距离走动量和速度走动量代表的距离索引和频率索引,按索引对相应的FFT结果进行相位补偿,相加取模后获取粒子适应度。不同段之间粒子的FFT结果存在相位差。粒子的距离走动量可表示为
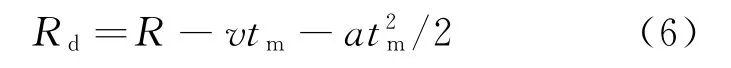
式中:为粒子的距离;为粒子的速度;为慢时间;为粒子的加速度。
粒子的速度走动量可表示为

不同段之间粒子FFT结果存在的相位差可表示为
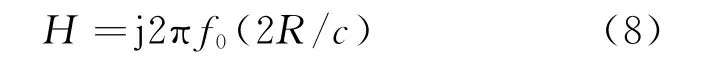
式中:为载频;为光速。通过比较粒子当前帧适应度值和粒子的历史最优适应度值,确定种群1和种群2粒子个体最优值是否更新。迭代次数=1,25,50时,不同迭代次数的粒子寻优过程分布如图2所示。可以看出两个种群的粒子均在逐渐收敛。
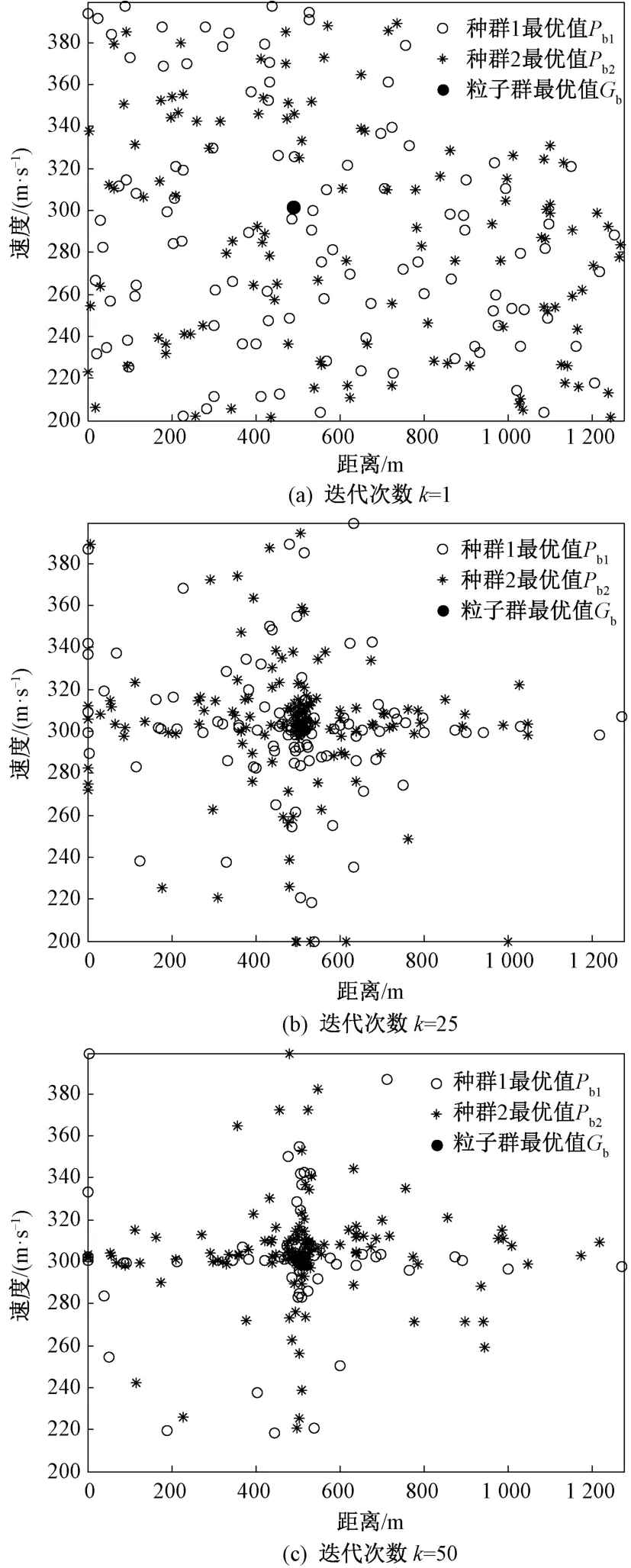
图2 不同迭代次数的粒子寻优过程分布图
将两个种群所有粒子的最优值作为粒子群最优值。粒子群更新即对所有种群所有粒子进行距离、速度和加速度的更新。两个种群同时对解空间搜索,不同种群之间通过种群交换进行信息交互,两个种群对交换部分的位置矢量再重新搜索,该算法模型能够有效避免过早收敛,降低陷入局部最大值的概率。粒子群更新包含两个种群,通过种群交换将粒子群的两个种群数据进行交换,对种群1和种群2的粒子按照适应度从小到大进行排序,交换种群1适应度最大的40个粒子与种群2适应度最小的40个粒子的个体值和最优值。
根据粒子群最优值的能量和噪声计算粒子群信噪比。判断粒子群信噪比是否满足要求。若信噪比大于13.0 d B,将粒子种群最优值作为终选目标。信噪比为27.3 d B,循环迭代200次的粒子寻优过程分布如图3所示。可知,粒子种群最优值的距离为509.2 m、速度为300.8 m/s、加速度为50.9 m/s,与仿真目标信号一致。
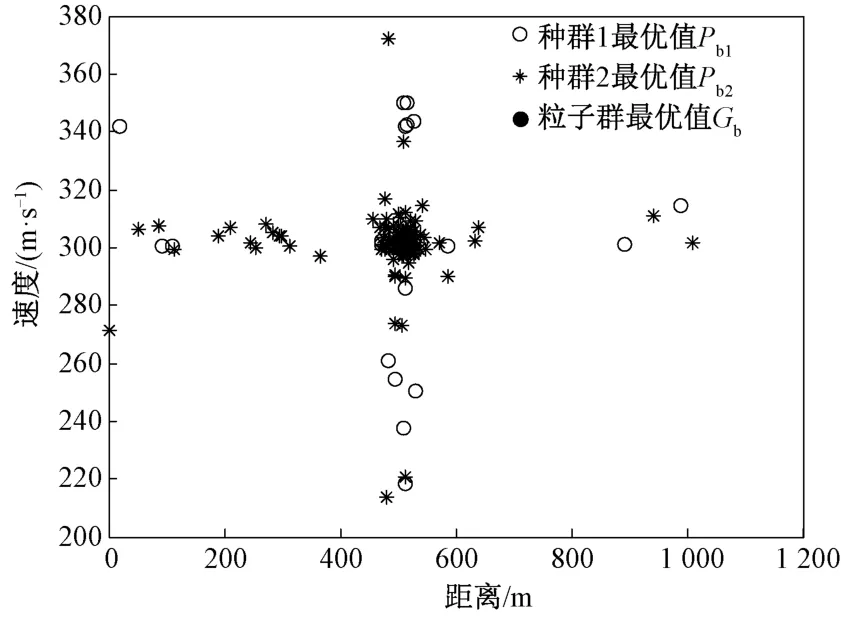
图3 迭代次数k=200时粒子寻优过程分布图
传统PSO算法采用固定权值种群寻找最优值,因为种群单一容易陷入早熟或停滞。多种群PSO算法加入了一个变权值种群,先进行全局搜索再局部搜索,在寻优过程中将部分固定权值种群粒子和部分变权值种群粒子进行交换,以保持寻优粒子群的多样性,可以达到较好的优化效果。
对两种PSO算法的适应度随迭代次数变化进行了仿真对比,如图4所示。
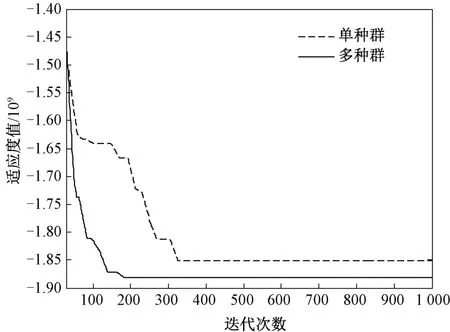
图4 适应度随迭代次数变化曲线
从仿真结果能够看出,多种群PSO算法收敛速度比单种群PSO算法更快。本文算法通过增加粒子群种群的多样性,使收敛到真实目标位置的迭代次数比传统PSO算法有所减少。在迭代中后期,多种群PSO算法要明显优于传统的单种群PSO算法,能够很好地抑制种群的停滞,避免种群陷入局部收敛。
4 结束语
提出了一种基于多种群的PSO算法,解决了雷达长时间回波积累过程中,目标机动导致回波数据跨距离和频率单元走动,造成积累检测性能下降的问题,可提高对隐身目标微弱回波信号的长时间相参积累增益。本文算法首先将回波数据进行分段FFT,使得每段内目标信号能相参积累,再根据两个种群中粒子的适应度大小,交换粒子个体值和最优值,可以有效避免算法陷入局部收敛。多种群PSO算法本质上是一种高效、快速的搜索方法,可以在预装的距离、速度和加速度集合范围内高效地寻找到目标真实距离、速度和加速度的匹配组合。

