微波雷达抗海杂波能力评估方法

江利中, 谭姗姗, 高林星, 陈 曦, 史秀花

(1.上海无线电设备研究所,上海 201109;2.华中科技大学人工智能与自动化学院,湖北 武汉 430074)

0 引言

当微波雷达工作在海洋环境中,雷达接收机将接收到大量的海杂波,目标回波信号往往淹没在海杂波中,对雷达的目标检测和跟踪性能产生相当程度的影响。当前,用户对微波雷达抗海杂波能力越来越关注,对其提出了明确的量化指标要求。因此,为了提高微波雷达的工作性能,开展雷达抗海杂波能力的论证和评估显得尤为重要。根据雷达抗海杂波性能的评估结果,可以衡量雷达的参数设计是否达标,进而优化参数设计,提升雷达抗海杂波能力。

本文提出一种利用信杂比与检测门限的相对关系来衡量雷达抗海杂波能力的评估方法,建立海杂波后向散射系数与雷达参数、海情之间的数学模型,确定衡量雷达抗海杂波能力的指标,并利用该方法对现有雷达的抗海杂波能力进行仿真与评估。

1 海杂波后向散射系数

国内外研究表明,海杂波回波与雷达波长、极化、入射角、海情、风向、风速等因素密切相关。常用的海杂波后向散射系数经验模型有佐治亚理工学院(Georgia Institute of Technology,GIT)模型、技术服务公司(technology service corporation,TSC)模型、混合(hybrid)模型以及Morchin模型。国内外研究机构对一系列海杂波模型进行了对比分析,发现GIT模型和TSC模型比较符合较小擦海角的情况。其中GIT模型是目前比较完善、也是应用最多的计算海杂波后向散射系数的模型,它综合考虑了极化、风向、风速、浪高等因素。

1.1 擦海角与距离的关系

擦海角为微波雷达波束中心与海平面的夹角,几何关系如图1所示。图中,为擦海角,为雷达距海平面的高度,为雷达的斜视探测距离。

图1 擦海角几何关系示意图

根据几何关系可知,擦海角的计算公式为

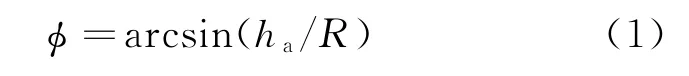
1.2 海杂波后向散射GIT模型

海表面的情况可以用海态数、蒲福风级、本地表面风速、均方根高度偏差和平均波高来表示。不同海情的海表面参数见参考文献[2]。

GIT模型是由佐治亚理工学院提出的针对单位面积的平均雷达散射截面确定参数模型。该模型是擦海角、风向、风速、平均波高、雷达波长和极化的函数。

海杂波水平极化归一化后向散射系数

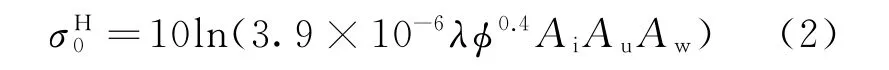
式中:为雷达波长;为干涉项,用于估计多径或干涉参数;为风向因子;为风速因子。

利用GIT海杂波模型,对海杂波后向散射系数进行仿真。设雷达工作在X波段,不同海情下海杂波垂直极化归一化后向散射系数的仿真结果如图2所示。其中图2(a)和图2(b)分别为逆风条件和顺风条件下的仿真结果。

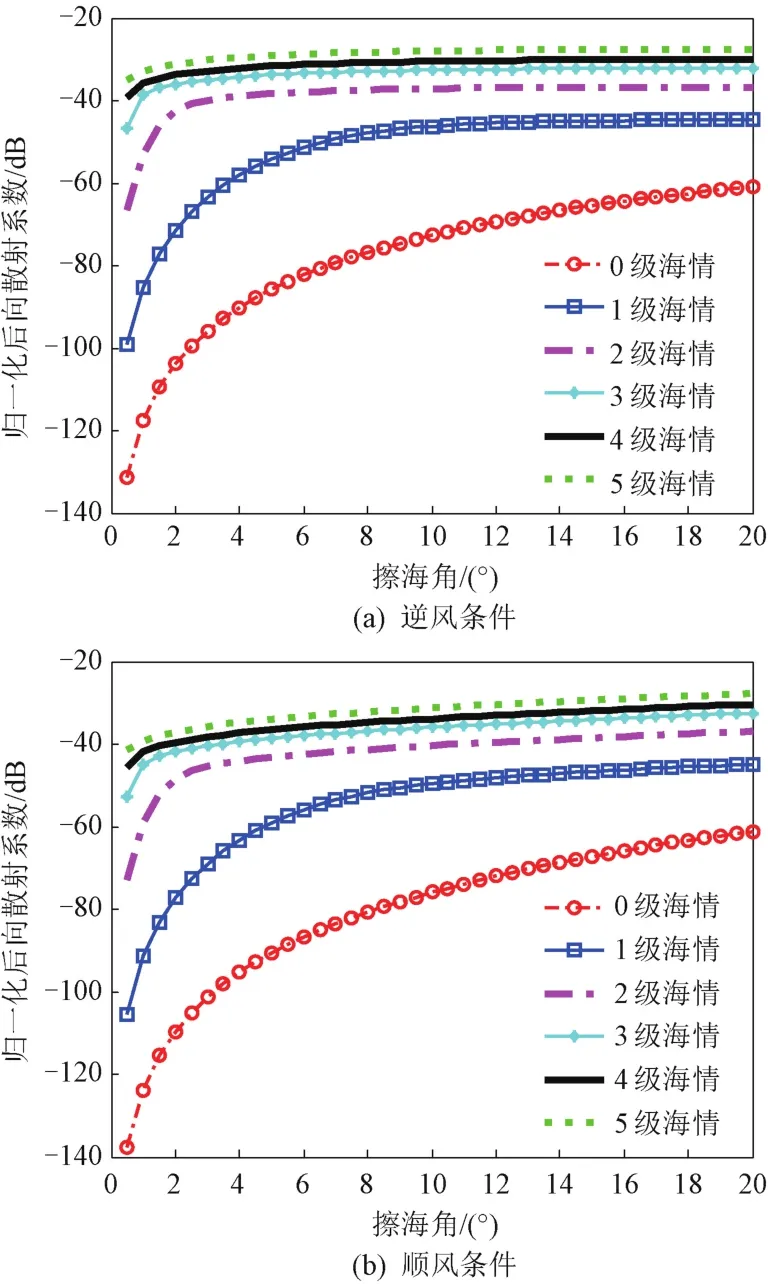
图2 不同海情下海杂波垂直极化归一化后向散射系数

可见,在其他参数相同的情况下,顺风与逆风对的影响较大,顺风情况下的较之逆风情况小(4～6)dB。因此,顺风情况下雷达回波信杂比将优于逆风情况。从这个角度来说,雷达天线轴线与逆风向之间夹角的选取对提高雷达抗海杂波性能较为重要。垂直极化条件下,擦海角为10°时,利用GIT海杂波模型仿真得到的3级海情所对应的归一化后向散射系数约为-33.8 dB。《雷达手册》所给出的海杂波后向散射系数曲线中,擦海角为10°时,3级海情所对应的后向散射系数约为-31.5 dB。二者十分接近,这说明了利用GIT模型仿真得到的海杂波后向散射系数的准确性。

2 海杂波雷达散射截面积计算

雷达单位距离分辨单元内的海杂波雷达散射截面积(RCS)主要由两个因素决定:一是海杂波的后向散射系数,二是单位距离分辨单元内的海杂波等效面积。在小擦海角的情况下,一个距离分辨单元内的海杂波雷达散射截面积

后向散射系数的水平及垂直极化分量的计算方法见式(2)和式(3)。

雷达在单脉冲跟踪阶段的海杂波对抗主要采用距离分割方式,减小海杂波截面积,从而有效地抑制单位距离分辨单元内的海杂波。雷达照射区域海杂波分割示意图如图3所示。

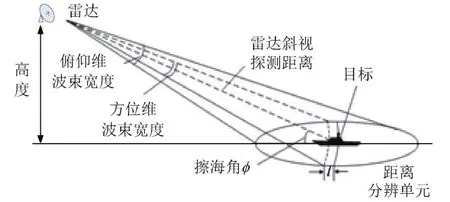
图3 雷达照射区域海杂波分割示意图

雷达单位距离分辨单元内海杂波的等效面积

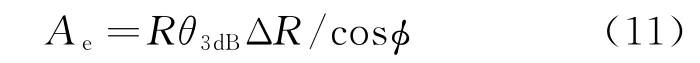
式中:为雷达天线的3 dB波束宽度;Δ为雷达的距离分辨率。

综合上述分析,计算海杂波RCS的步骤如图4所示。

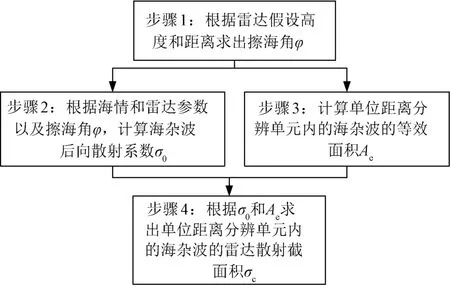
图4 海杂波RCS计算步骤示意图

设雷达高度为400 m,天线3 dB波束宽度为8°,雷达距离分辨率为3.75 m,采用垂直极化。对不同海情和不同风向条件下的海杂波RCS进行仿真,结果如图5所示。可知,顺风条件下的海杂波RCS比逆风条件下小。

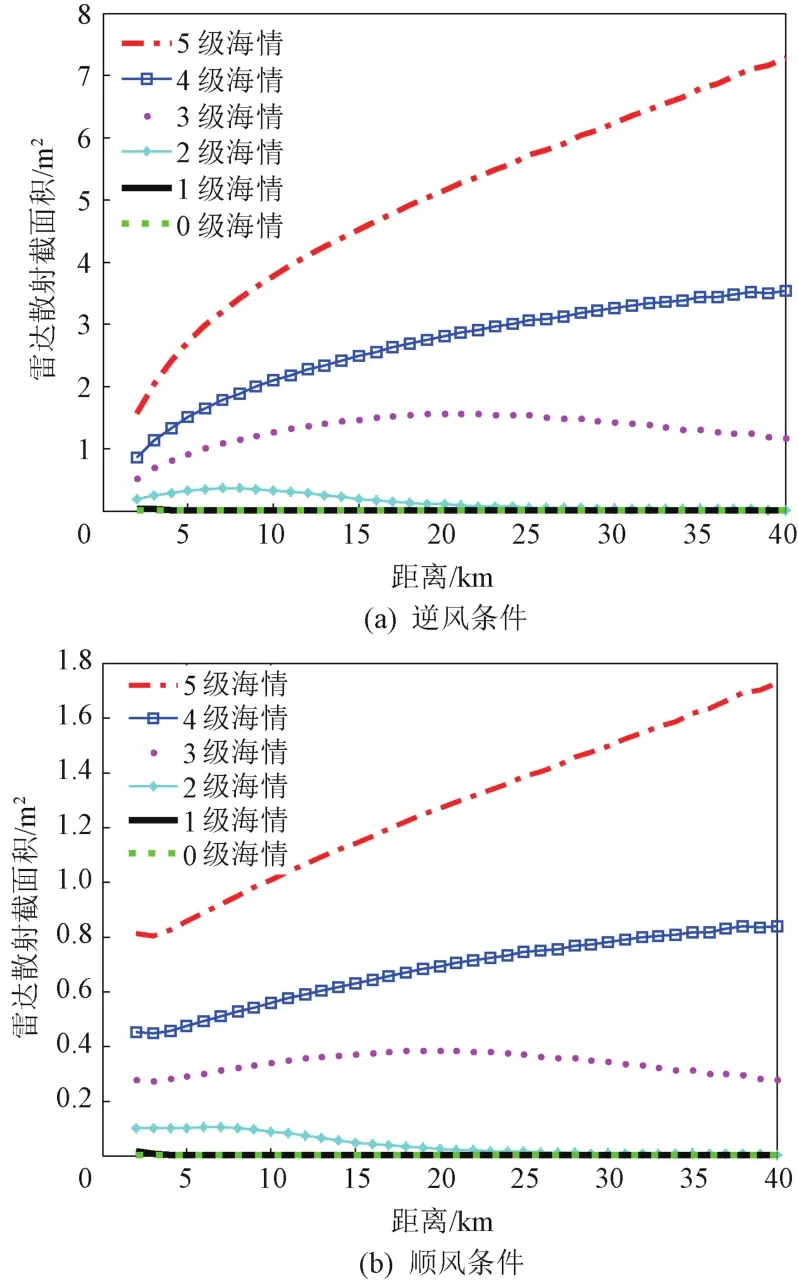
图5 不同海情不同风向条件下的海杂波RCS

3 微波雷达抗海杂波能力评估方法

当海杂波和目标回波信号同时进入雷达的接收通道,能否将目标信号从杂波中检测出来,取决于信杂比是否能够达到雷达的检测门限,而信杂比主要取决于目标RCS和海杂波RCS的相对比值。若雷达采用捷变频或者其他海杂波去相关信号处理方法,则能够进一步提高目标RCS和海杂波RCS相对比值,提升雷达的抗海杂波能力。

假设雷达单位距离分辨单元内的海杂波RCS为,目标RCS为,由于信号处理而带来的信杂比增益为,则信杂比

根据信号检测理论,在海杂波环境中,信杂比是衡量雷达抗海杂波能力的关键指标。越大,则目标检测概率越高,雷达的抗海杂波性能越好。设雷达的信号检测门限为,则可通过与之间的关系,来衡量雷达抗海杂波的能力。若≥,则检测判决目标存在,表明目标未被海杂波淹没,雷达能够对抗海杂波干扰;若＜,则检测判决目标不存在,表明目标被海杂波淹没,雷达不能对抗海杂波干扰。

在雷达设计的前期,通过本方法可评估雷达的抗海杂波能力是否满足指标要求,进而完善雷达设计参数。通过提高雷达距离分辨率、减小擦海角、去除海杂波相关性、优化雷达高度等技术手段进行参数优化,可以使微波雷达的抗海杂波能力满足指标需求。

4 微波雷达抗海杂波能力评估验证

设雷达工作频段为X波段,天线垂直极化,波束宽度为7°,雷达距海平面高度为400 m,距离分辨率为3.75 m,目标RCS为20 m,目标检测门限为14 d B,信号处理增益为2 dB。验证逆风条件和顺风条件下该雷达的抗海杂波能力。

(1)逆风条件

在逆风条件下,对不同海情下该雷达的信杂比与检测门限关系进行仿真,如图6所示。

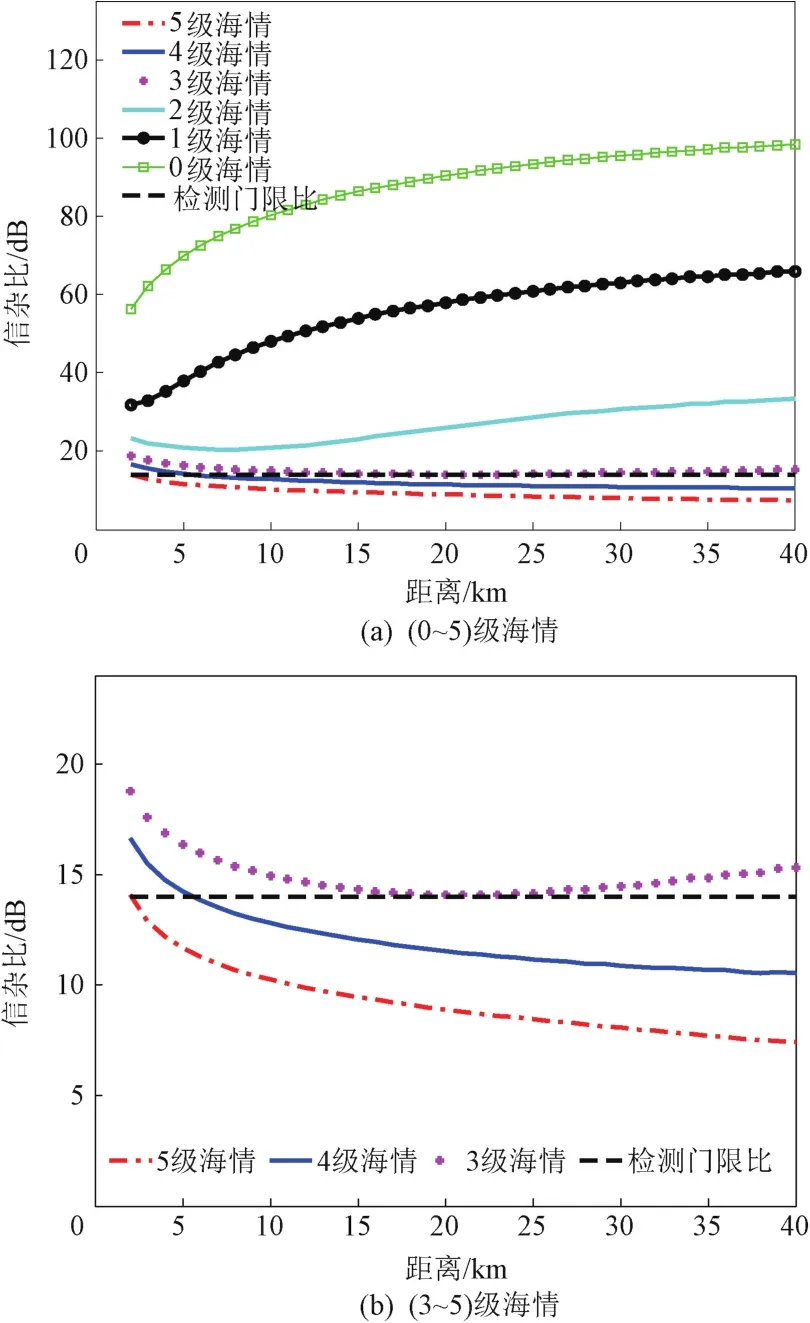
图6 逆风条件下不同海情雷达信杂比与检测门限的关系

由图6(a)可知,(0～3)级海情下,(2～40)km的距离范围内,信杂比均高于检测门限,说明该雷达可全程对抗海杂波。由图6(b)可知,3级海情下,近距离区间内,由于距离的增加导致单位距离分辨单元内的海杂波等效面积增加,信杂比随着距离的增加而降低;而在(20～40)km的距离范围内,由于擦海角的减小,海杂波后向散射系数急剧下降,使得信杂比逐渐增大。

4级海情下,仅在(2.0～5.4)km的距离范围内,信杂比大于检测门限;在(5.4～40.0)km的距离范围内,信杂比小于检测门限,无法探测到目标。说明在逆风4级海情的条件下,该雷达抗海杂波能力较弱,仅能对抗5.4 km以内的海杂波。而5级海情下,在所有距离范围内信杂比均小于检测门限,雷达无法对抗海杂波。

(2)顺风条件

在顺风条件下,对不同海情下该雷达的信杂比与检测门限关系进行仿真,如图7所示。

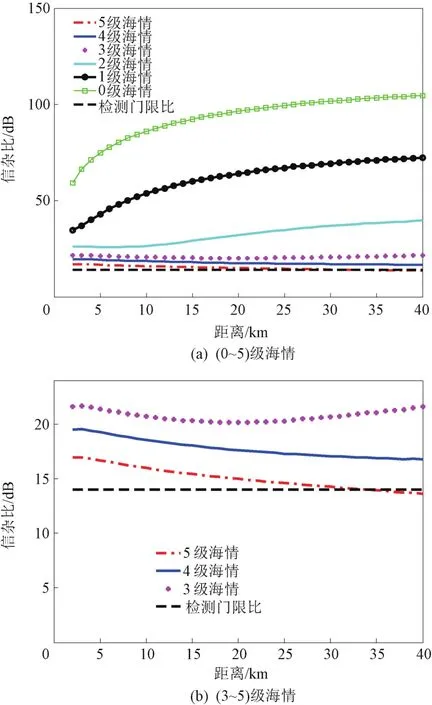
图7 顺风条件不同海情下雷达信杂比与检测门限的关系

由图7(a)可知,(0～4)级海情下,(2～40)km的距离范围内,信杂比均高于检测门限,说明该雷达可全程对抗海杂波。由图7(b)可知,5级海情下,(2～33)km距离范围内,信杂比大于检测门限,该雷达能够对抗海杂波;当距离大于33 km后,信杂比小于检测门限,目标被海杂波淹没,该雷达不能对抗海杂波。

综上所述,雷达在逆风条件下,可全程对抗(0～3)级海情下的海杂波,仅能对抗4级海情下距离在5.4 km以内的海杂波,无法对抗5级海情下的海杂波。在顺风条件下,该雷达可全程对抗(0～4)级海情下的海杂波和5级海情下距离在33 km以内的海杂波。

5 结束语

本文详细论述了海杂波RCS与雷达参数、海情、风向、极化之间的关系,并给出了海杂波RCS的详细计算方法。同时,综合考虑信号处理算法带来的信杂比增益等相关因素,提出了利用信杂比与检测门限之间的相对关系来衡量微波雷达的抗海杂波性能的评估方法,并基于具体的雷达参数设计,对该雷达的抗海杂波能力进行了仿真与评估。仿真结果表明,本文提出的抗海杂波性能评估方法能够衡量雷达在海洋环境中的工作性能,有助于在雷达设计前期优化系统参数,提升雷达的整体性能。