感应电机无源性迭代学习转速控制
王璐 ,范波 ,邱玉林
(1.河南科技大学信息工程学院,河南 洛阳 471003;2.中信重工机械股份有限公司,河南 洛阳 471003)
感应电机由于结构简单、价格低廉等特点,在工业领域得到广泛应用,其有效控制方法的研究一直受到大家的重视[1]。由于感应电机复杂多变、耦合性强的非线性运行特征,难以采用传统的线性系统控制方法来获得高性能的感应电机转速控制器。为了得到更好的控制效果以满足工业领域不断提高的性能需求,许多非线性控制方法被应用于感应电机控制领域,例如反馈线性化、反步法、滑模控制及智能控制等[2-3]。
无源性方法于1989年被Ortega R与Spong M提出[4]。将其应用于感应电机控制系统,可以从能量的角度将感应电机与控制器看作能量输入、输出转换装置,通过能量注入和互联达到控制平衡,在抑制外界扰动影响的同时,使电机系统的输出信号能够有效跟踪给定信号。
本文基于无源性控制理论,设计感应电机的无源转速控制器,并构建迭代学习控制器来引入自学习能力。在此基础上,为进一步改善动态响应性能,对转速给定值进行柔化处理,同时在迭代学习过程中加入微分项。仿真表明,电机转速响应能够很好地跟随柔化给定值,转速无超调,控制性能良好。
1 感应电机的无源性控制设计
1.1 感应电机运动数学模型
在d-q旋转坐标系下,感应电机的动力学模型由绕组电压方程和机械运动方程组成[5-6]。
电压方程如下:
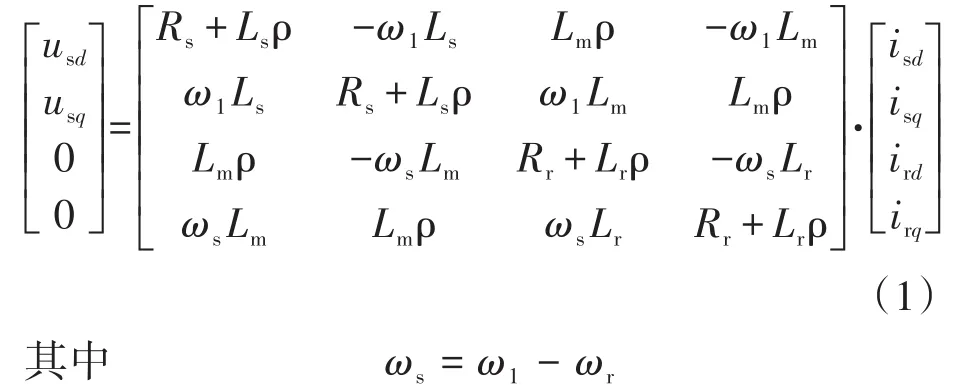
式中:isd,isq分别为定子电流在d,q轴上的分量;ird,irq分别为转子电流在d,q轴上的分量;usd,usq分别为定子电压在d,q轴上的分量;ωr为转子角速度;ω1为旋转角速度;ωs为转差角速度;Rs,Rr分别为电机定子和转子电阻;Ls,Lr分别为定子绕组和转子绕组的等效自感;Lm为定子和转子绕组的等效互感;ρ为微分算子。
机械方程如下:
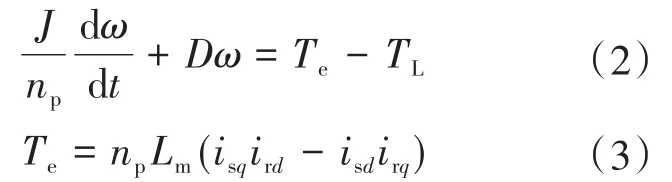
式中:J为转子转动惯量;D为阻尼系数;TL为负载转矩;Te为电磁转矩;ω为电机转速;np为磁极对数。
1.2 感应电机的无源性分析
使用Eluer-Lagrange方程表达感应电机系统的总能量,并附加耗散项注入。与基于系统自然耗散所得收敛性相比,附加耗散项可以改善导出状态的收敛性[7]。感应电机无源性控制方法将系统分为电气和机械两个系统[8]。为保证系统的全局稳定,将机械系统看作扰动,以证明电气系统无源。
具体来说,取ix=[isdisqirdirq]T为状态变量;ue=[usdusqurdurq]T为控制输入;并令Ι2为单位矩阵,则有:


由式(4)~式(8)及电气系统方程可知,感应电机的Euler-Lagrange系统方程为

式(9)中,等号左边第1项为系统的作用力;因Re矩阵正定,则第3项为系统的耗散力;第4项为外部扰动。在式(9)两边同乘,由于是系统的无功分量,不影响系统的能量平衡。可得:

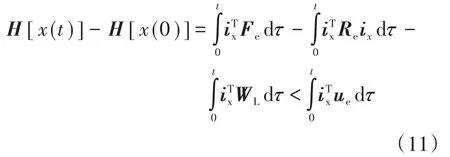
等号左侧代表能量的变化量,等号右侧各项为感应电机由外部输入的能量变化。根据无源性理论,可以证明感应电机的电气系统为严格无源。同理可证得机械系统亦为严格无源。在控制器设计过程中,为了在减少控制难度的同时满足控制性能要求,可将机械部分作为系统的无源扰动,电气系统则为受控对象。
2 感应电机转速控制器设计
根据上述无源性控制的分析,感应电机无源控制器的设计是系统的输出转矩和磁链跟随期望[9]。因此结合磁场定向原理可得到:

式中:T′e为系统期望转矩;i′sd,i′sq为对应于T′e的期望定子电流在d,q轴上的分量;i′rd,i′rq分别为对应于T′e的期望转子电流在d,q轴上的分量;Ψ′r为对应T′e的期望磁链。
定义系统状态向量为x=[isdisqirdirq]T,x′=[i′sdi′sqi′rdi′rq]T,则系统期望状态变量的误差向量为ex=x-x′,结合式(9)可知感应电机系统加入误差向量后的方程为

式中:ζe为系统扰动。

由于Re函数为正定的,因此只有当ζe=0时,e<0,则误差ex收敛到0,转矩趋近收敛于期望值,为实现ζe=0,达到控制效果,结合感应电机的特性及矢量控制磁场定向原理,使在d,q轴上的转子磁链分量分别满足以下条件:

其中,Ψ′r是常值,令i′rq=0可以得到转子电流在d,q轴上的分量及转差率如下所示:
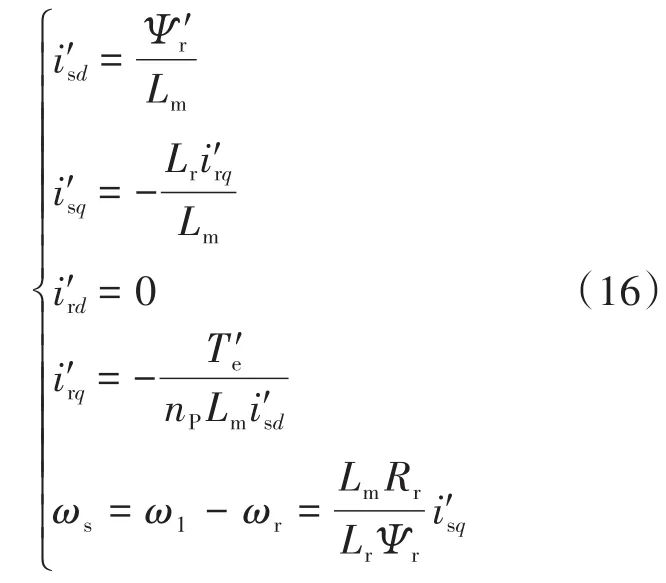
综合以上分析,可以得到无源控制器如下:
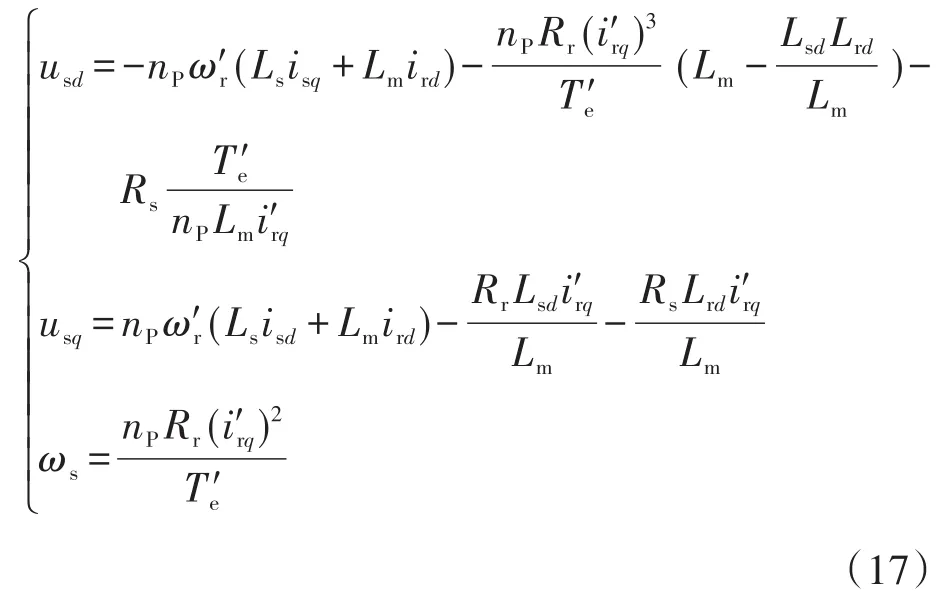
式中:ω′r为转速给定值。
为了降低系统对参数变化的反应程度,并且保证闭环系统严格无源,达到快速响应的目的,引入阻尼系数K,构成阻尼项。阻尼项方程如下所示:
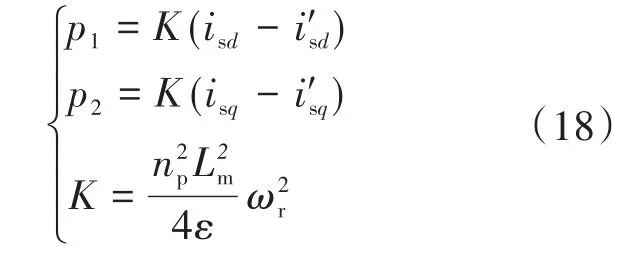
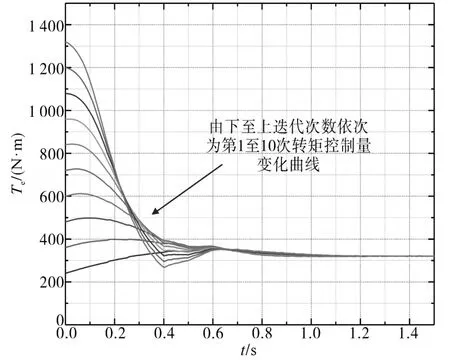
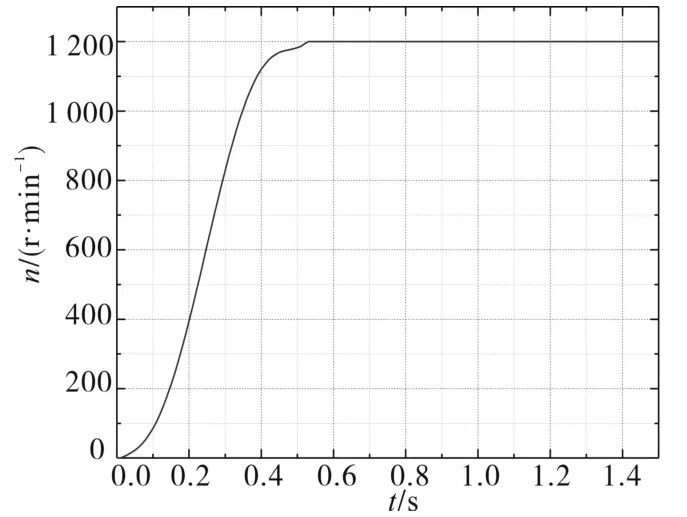
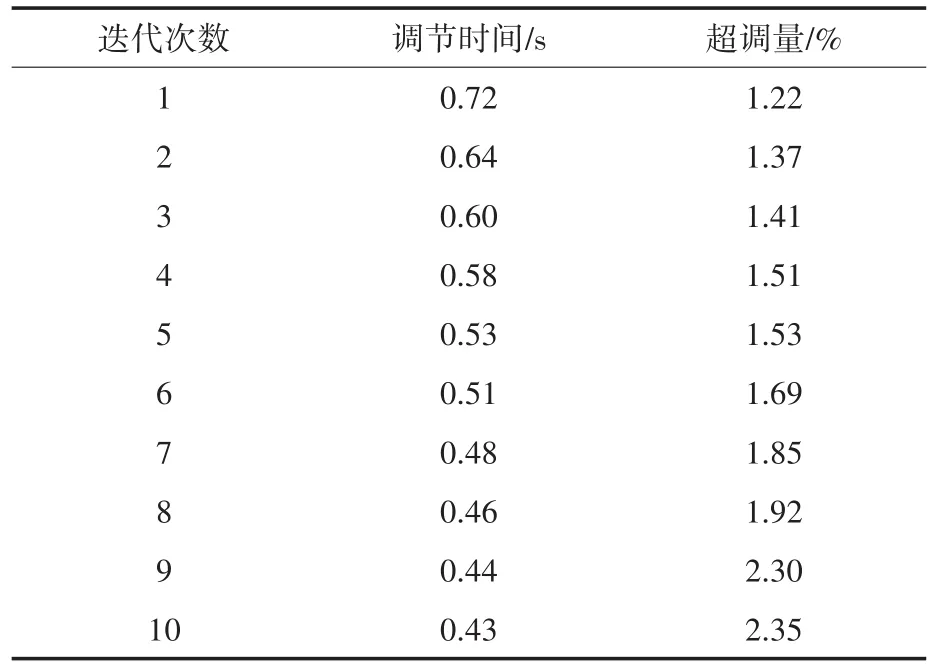
式中:ε为常数,且 0< ε 在感应电机转速控制设计中,本文设计为无传感器控制方式,基于磁链模型来在线估计电机转速。对转子磁链的d,q轴分量之差进行比例积分运算,从而得到估计的转速值: 基于前述无源性分析结果,转速控制器可设计为 式中:Kp1,Ki1分别为比例增益、积分增益。 迭代学习控制(iterative learning control,ILC)不依赖于被控对象的精确数学模型,其自学习能力可以使系统在重复运行过程中不断逼近控制期望,且具有控制算法计算量小、实现成本低的优点[10-12]。本文中,设计感应电机P型迭代学习控制器如下: 式中:ui(t),ui+1(t)分别为系统第i次和第i+1次运行过程中t时刻的输出控制变量;ei(t)为第i次运行过程中t时刻的转速误差;kp为比例学习增益。 由式(21)可知,迭代学习的控制过程是基于前一次控制情况的学习过程。因而,系统第1次运行采用式(20)所示控制器,为随后的迭代学习控制进程提供学习基础。 为验证迭代学习转速控制性能,搭建Simu⁃link系统仿真模型,如图1所示。 图1 感应电机无源性迭代学习转速控制结构图Fig.1 Passivity iterative learning speed control structure diagram of induction motor 感应电机参数设置为:PN=2.2 kW,UN=380 V,ωN=1200 rad/s,Lsd=Lrd=2 mH,J=0.03kg ⋅m2,Rr=0.816Ω,Rs=0.435Ω,np=2,Lm=69mH,期望磁链设为0.9 Wb,感应电动机空载启动。 取kp=0.1,将学习迭代次数设置为10次,得转速阶跃响应过程如图2所示,对应的转矩控制量变化曲线如图3所示。 图2 迭代学习控制系统的转速响应曲线(kp=0.1)Fig.2 Speed response curves of iterative learning control system(kp=0.1) 图3 转矩控制量变化曲线(kp=0.1)Fig.3 Torque control variation curves(kp=0.1) 从图2可以看出,随着迭代次数增加,转速上升时间逐渐减少,迭代学习控制有效。但从第4次迭代开始,出现明显的超调。这表明,P型迭代学习控制虽然能够使转速响应过程逐渐趋近阶跃给定值,但也导致了超调。图3表明,为了更快达到转速阶跃给定值,电机转矩随着迭代次数的增加而不断增大,导致控制量不断增大,过大的转矩必然导致超调。产生超调的原因首先来自于转速给定值为阶跃函数。在迭代学习过程中,初始时刻的转速为0,转速误差值大。系统为了减少转速误差,必然使控制量不断增大,使转速响应过程出现超调。 为了解决系统阶跃给定值以及电机模型惯性引起的系统超调,对转速阶跃给定值进行柔化处理,使柔化后的给定值按照一定的方式光滑趋近阶跃给定值。通过图2中的转速数据分析,选取第2次迭代学习的转速进行曲线拟合,并对拟合的结果进行处理得到柔化表达式为 柔化的主要目的是配合迭代学习使系统的输入量达到合理给定,从而避免在迭代学习过程中出现超调。柔化后的转速给定值曲线如图4所示。取kp=0.14,迭代10次的电机转速响应曲线如图5所示,转矩变化曲线如图6所示。 图4 转速给定值柔化后的曲线Fig.4 Speed setting curve after softening 图5 给定柔化后的迭代学习控制系统的转速响应曲线(kp=0.14)Fig.5 Speed response curves of iterative learning control system after softening(kp=0.14) 图6 给定柔化后的转矩控制量变化曲线(kp=0.14)Fig.6 Torque control variation curves after softening(kp=0.14) 由图5可知,对阶跃给定值进行柔化处理后,转速响应的超调明显减小,并能够通过迭代学习来逐渐趋近柔化给定曲线。图6表明,随着迭代次数的增加,转矩在转速上升过程中逐步增加,使转速上升速度合理加快。 迭代学习控制系统的转速性能指标如表1所示,系统在10次迭代学习过程中,随着学习迭代次数的增加,上升时间逐渐缩短,超调得到明显抑制。 表1 迭代学习控制系统的转速性能指标(kp=0.14)Tab.1 Speed performance index of iterative learning control system(kp=0.14) 为了进一步抑制超调,同时保证响应的速度,在式(21)所示控制器中加入微分项,得到PD型迭代学习控制器为[13] 式中:kd为微分学习增益;ωr0(t)为系统在第i次运行过程中t时刻的转速。 取kp=0.14,kd=0.9,迭代10次的转速响应曲线如图7所示,对应的迭代学习转速性能指标如表2所示。 图7 给定柔化后的迭代学习控制系统的转速响应曲线(kp=0.14,kd=0.9)Fig.7 Speed response curves of iterative learning control system after softening(kp=0.14,kd=0.9) 表2 迭代学习控制系统的转速性能指标(kp=0.14,kd=0.9)Tab.2 Speed performance index of iterative learning control system(kp=0.14,kd=0.9) 由图7及表2数据与P型对比可知,当系统的上升时间减少、调节时间缩短时,PD型迭代学习的转速超调量得到进一步控制,控制性能趋好。 本文首先在无源控制理论的基础上对感应电机的无源性进行分析并设计无源控制器,接着在感应电机的转速控制中加入迭代学习的控制算法,采用P型迭代学习控制器时仿真发现系统有超调,产生超调的原因是由于转速给定为阶跃函数,在跟随给定转速的过程中,由于实际转速与给定转速存在误差,导致控制量增大,同时在控制作用下电机模型存在惯性,因此发生超调。为了解决该问题,通过将给定阶跃信号进行柔化,使给定转速以一定的方式趋近给定转速,实现了转速控制超调的抑制。最后为了进一步抑制系统超调,加入微分项构成PD型迭代学习控制器,系统转速曲线响应无超调,跟随性能良好。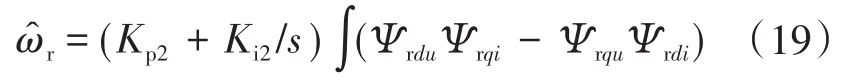
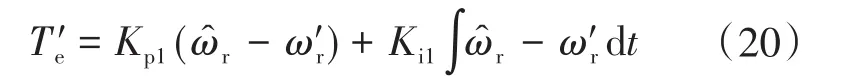
3 感应电机迭代学习转速控制器
3.1 P型迭代学习转速控制器
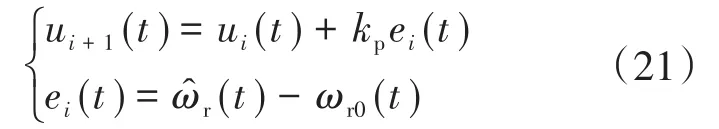


3.2 引入给定值柔化的迭代学习转速控制器



3.3 PD型迭代学习转速控制器
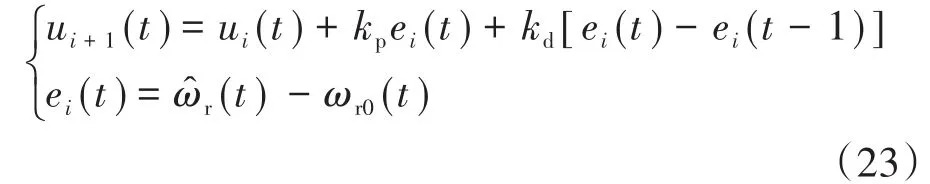


4 结论

