感应电机基于转矩预测控制方法研究

陈虎，王阳阳，潘月斗

（1.中国航空制造技术研究院，北京 100024；2.北京科技大学工业过程知识自动化教育部重点实验室，北京 100083）

直接转矩控制（direct torque control，DTC）具有结构简单、转矩响应快以及对参数鲁棒性好等优点，但也存在低速时转矩脉动较大[1]的问题。针对这一问题，学者提出了一些解决方案，如基于空间矢量调制的直接转矩控制[2]、基于无差拍空间矢量的直接转矩控制[3-4]、基于占空比调制的直接转矩控制[5-6]和基于模型预测的直接转矩控制[7]等。

文献[2]采用了一种基于空间矢量调制技术的DTC控制算法。该算法减小了输出转矩脉动，同时获得恒定的开关频率，但计算量复杂，且过于依赖电机参数；文献[3]提出了一种简化的无差拍空间矢量调制的DTC控制算法，虽简化了一些实时求解一元二次方程的复杂度，但仍不能同时保证磁链和转矩的无差控制，且计算过程中对参数依赖较大，降低了对电机参数的鲁棒性；文献[5]提出一种基于8开关三相逆变器的DTC控制算法。该算法分析了各扇区内转矩、磁链以及直流侧两电容电压的大小随电压矢量的变化情况，同时平衡直流侧两电容电压的目标，并设计了新的矢量选择开关表，但该方法无法摆脱电压矢量不能同时始终满足磁链和转矩控制要求的弊端。

本文将广义预测控制（generalized predictive control，GPC）[8-10]引入到直接转矩控制中，提出基于受控自回归积分滑动平均模型（control auto re⁃gressive integrated moving average，CARIMA）的感应电机广义预测控制方法。在直接转矩控制的基础上预测控制电机的转速，并由广义预测控制算法计算并输出最优转矩控制量，进而使直接转矩控制中的空闲开关周期得到充分利用。该方法不仅具有直接转矩控制的各种优点，同时也有效地减小了直接转矩控制算法本身由于电压矢量在控制周期内持续作用于电动机所产生的转矩脉动。最后，通过仿真及实验展现了广义预测控制算法在直接转矩控制中的应用，并与传统直接转矩控制方法进行了对比，验证了广义预测控制算法的可行性和优越性。

1 感应电机CARIMA模型

为引入感应电机的CARIMA模型，参考电动机旋转运动方程[11]如下：

式中：J为转子和负载的转动惯量；Te为电机的电磁转矩；TL为负载所引起的阻力矩；np为电机极对数；ωr为转子角速度。

令Te-TL=T∗，对式（1）进行拉普拉斯变换，得：经过零阶保持器采样后，有：

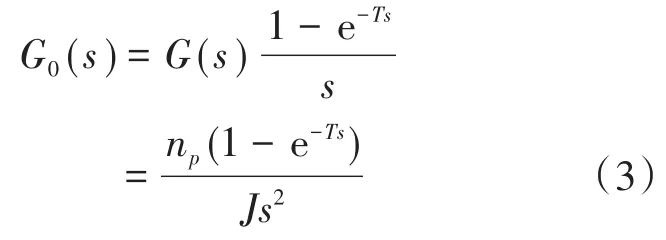
式中：T为采样周期。

对式（3）进行z变换求其脉冲传递函数，得：

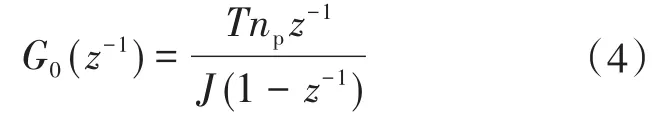
根据广义预测控制理论[8-10]，单输入单输出（single-input single-output，SISO）系统的CARIMA模型为

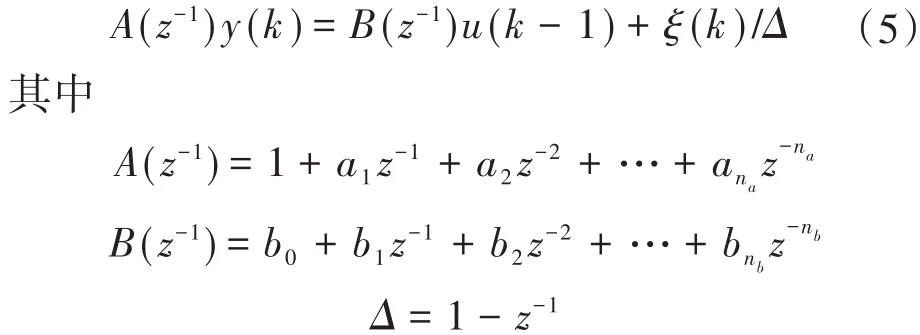
式中：Δ为差分算子；{ξ(k)}为均值是零的白噪声序列；a1，a2，…ana，b1，b2，…，bna分别为A(z-1)和B(z-1)的多项式系数；na，nb分别为A(z-1)和B(z-1)的多项式阶次。

可得由输入u到输出y之间的脉冲传递函数如下式所示：

令G0(z-1)=G(z-1)，对照系数有：

令输入u(k)=T∗(k)，输出y(k)=ω(k)，则可以得到电动机旋转运动的CARIMA模型如下式：

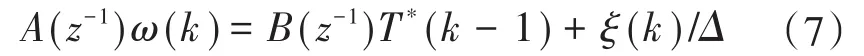
2 GPC的控制结构最优控制律

建立CARIMA模型后，引入Diophantine方程[8-10]：

联立式（7）～式（9），k时刻的预测输出如下式：

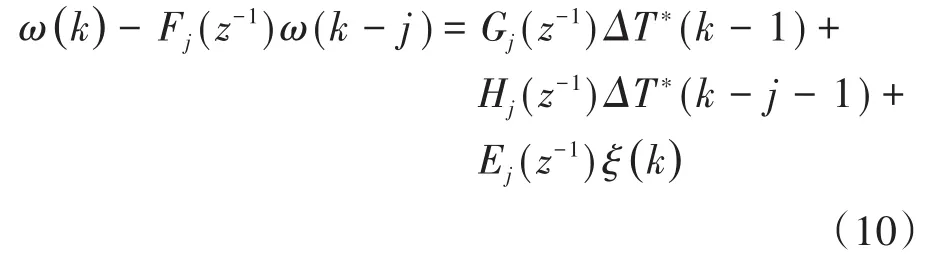
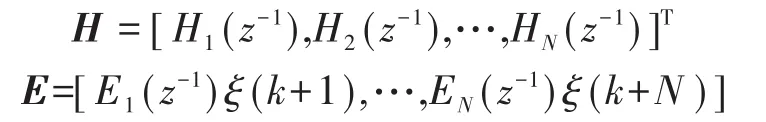
写成向量形式，有：式中：ω(k)为不同时刻输出的转速矢量；T*(k-1)为不同时刻输出的电磁转矩矢量；F，G为系数矩阵；N为终止时刻。

广义预测控制的控制目的不是使输出直接跟踪设定值，而是跟踪参考轨线。参考轨线一般选用一阶滤波方程[8-10]参考序列如下：

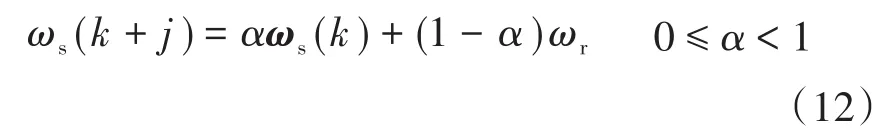
进而，性能指标函数可取：式中：λ为加权系数。

将式（10）代入式（12），则使J取得最小值的控制规律为

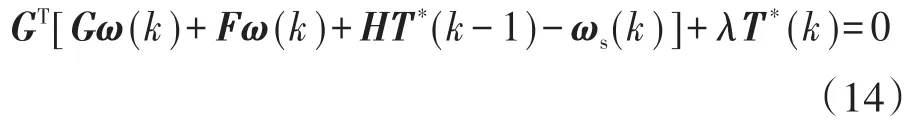
整理得：

式中：I为单位矩阵。

记(GTG+λI)-1GT的第1行为dT=[d1,d2,…,dN]，且定义d(z-1)=dN+dN-1z-1+…+d1z-(N-1)。于是由滚动优化和反馈校正原理可将广义预测控制规律写成下式：

3 GPC的控制结构

根据求得的GPC控制算法最优控制律，采用Simulink中的S-Function自定义函数模块编写广义预测控制算法，其控制算法流程图如图1所示。

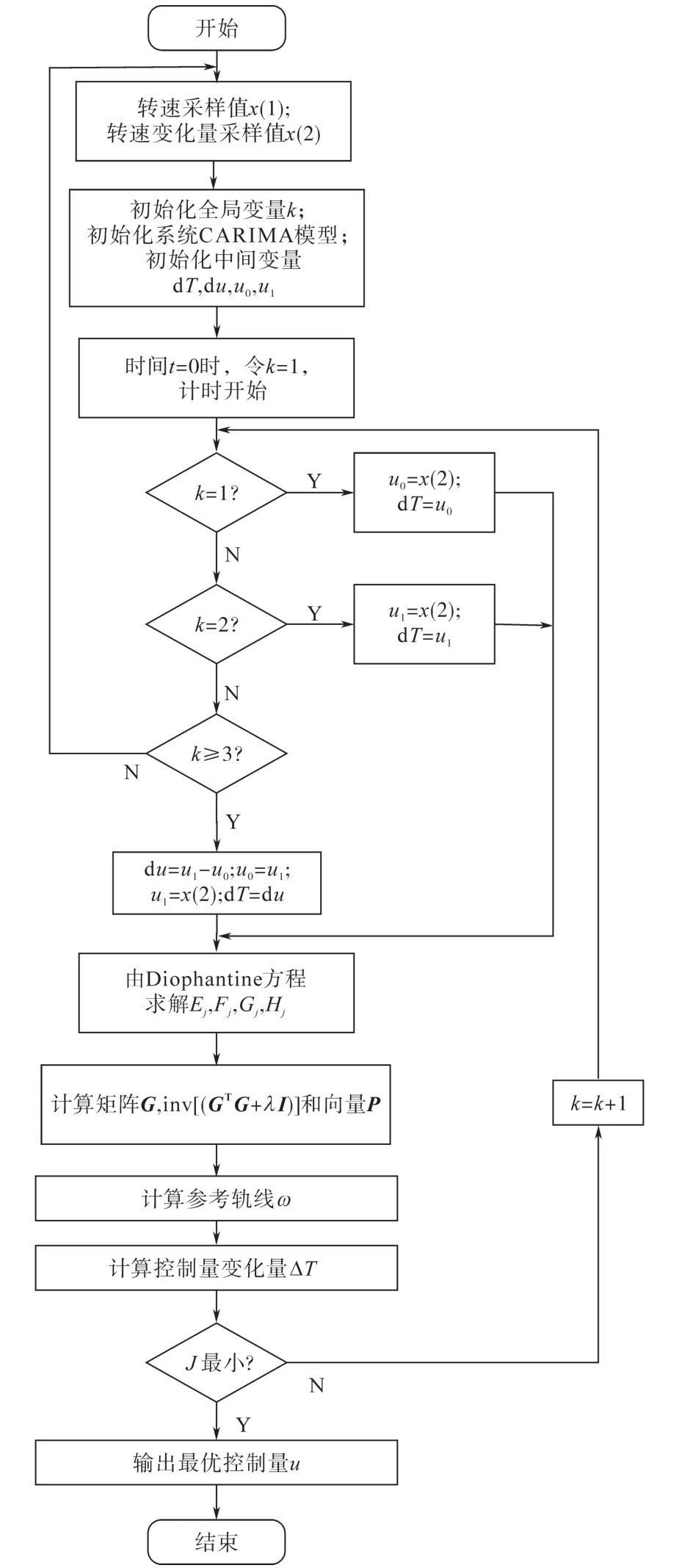
图1 GPC控制算法流程图Fig.1 Flow chart for GPC control algorithm

4 系统仿真与实验

4.1 系统仿真

为了验证本文提出的GPC控制算法在感应电机低速时的性能优点，运用Matlab进行仿真，仿真模型如图2所示。

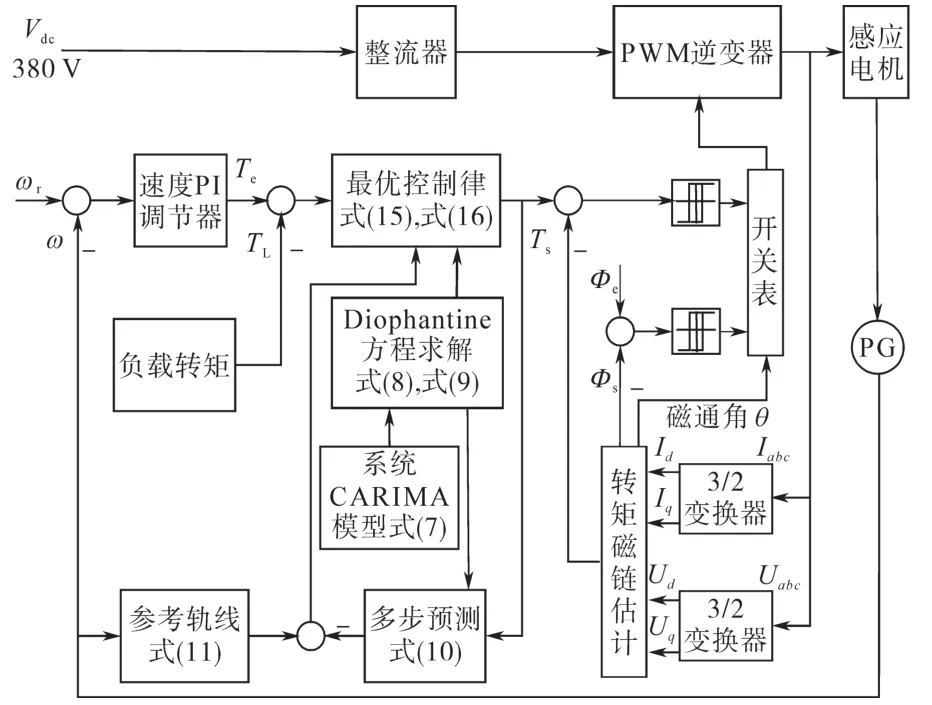
图2 GPC控制算法仿真模型Fig.2 Simulation model of GPC control algorithm

感应电机主要参数选择如下：额定功率PN=2 238 W，额定电压UN=220 V，额定频率ƒN=50 Hz，额定转速nN=1 440 r/min，定子每相绕组电阻RS=0.435 Ω，转子每相绕组电阻Rr=0.816 Ω，定子每相绕组自感LS=0.004 H，转子每相绕组自感Lr=0.002 H，定、转子间的互感M=0.06 931 H，极对数np=2，转动惯量J=0.089 kg·m2。此外，系统采样周期为50 μs，给定参考磁链值为0.9 Wb。

为验证两种控制算法在低速时的控制效果，给定转速设定为额定转速的10%，即144 r/min。为了对比控制效果，先后采用了DTC控制算法和GPC控制算法，并给出了不同控制方法时的磁链、负载转矩、转速及电流响应曲线。

图3为仿真时间0.02 s时，两种控制方法作用时的磁链幅值响应曲线。可以发现，虽然采用两种控制方法的曲线最终都稳定于给定参考磁链值0.9 Wb，但DTC控制算法的上升时间约为0.01 s，而GPC控制算法的上升时间约为0.006 s，缩短了约40%；DTC控制算法的调节时间约为0.012 s，而GPC控制算法的调节时间约为0.007 s，缩短了约41.7%。由此可见，GPC控制算法动态响应效果较好。

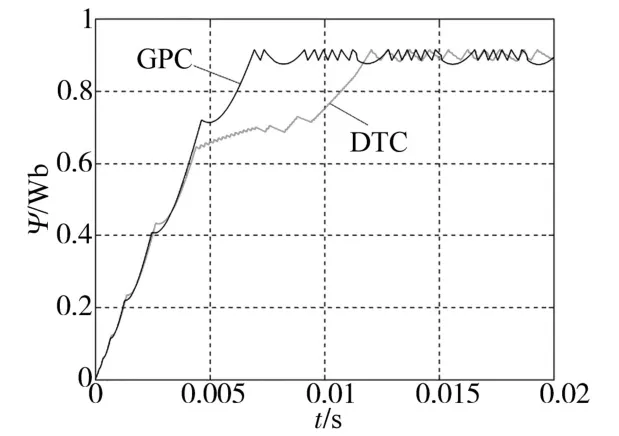
图3 磁链幅值响应曲线Fig.3 Response curves of flux amplitude

图4为加入负载的转矩响应曲线。可以看出，到达稳态后，DTC控制算法的转矩脉动约为10 N·m，而GPC控制算法产生的转矩脉动约为3 N·m，仅为DTC控制算法转矩脉动的1/3，从而验证了低速时GPC控制算法在抑制转矩脉动时的可行性与有效性。

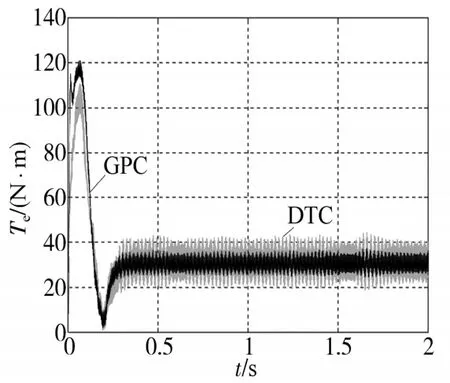
图4 负载转矩响应曲线Fig.4 Response curves of torque

对于转速响应，GPC控制算法的优越性则更为明显，如图5所示。从图5中可以很明显地看到，DTC控制算法在1.5 s后转速达到额定转速，而GPC控制算法只需约0.3 s，达到额定转速时间较传统DTC算法明显缩短。

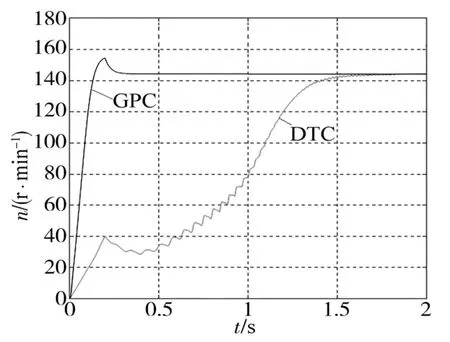
图5 转速响应曲线Fig.5 Response curves of speed

电流响应曲线如图6所示。同样可以发现，DTC控制算法的电流响应曲线收敛较慢，约0.9 s时仍有较大波动，而GPC控制算法则迅速收敛且在约0.25 s即达稳态，显示了较好的快速性和稳定性。

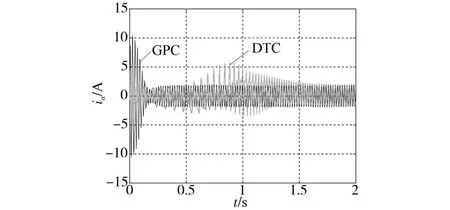
图6 电流响应曲线Fig.6 Response curves of current

4.2 实验验证

为了进一步验证GPC控制算法的可行性与有效性，搭建了实验平台，系统的硬件系统的结构框图如图7所示。

图7 系统硬件框图Fig.7 Hardware block diagram of system

系统的控制器采用美国TI公司的控制板DSP（TMS320F2812），该芯片为电动机专用控制器芯片，内含丰富的速度检测及PWM输出等功能。主回路采用日本三菱公司产的IPM智能功率模块，与IGBT相比，性能和可靠性有进一步的提高。IPM集成了驱动和保护电路，动态损耗和开关损耗都比较低，散热器减小，系统尺寸也减小。IPM在故障情况下的自保护能力降低了器件在使用中的损坏机会。电机参数采用第4.1节中的仿真电机参数，控制策略分别采用DTC控制算法和GPC控制算法。

图8～图11给出了DTC控制算法和GPC控制算法的磁链、负载转矩、转速及电流的实验波形。可以看出，系统在低速调速范围内具有良好的性能，验证了GPC控制算法的可行性与有效性。

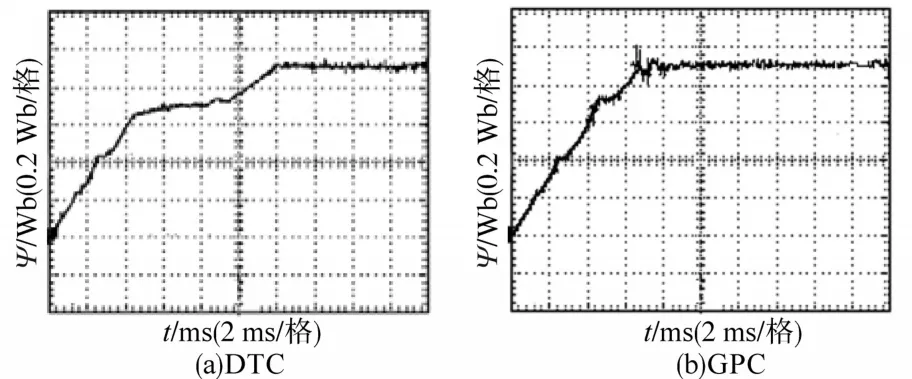
图8 磁链幅值响应实验波形Fig.8 Experimental waveforms of response of flux amplitude

图9 负载转矩响应实验波形Fig.9 Experimental waveforms of response of torque

图10 转速响应实验波形Fig.10 Experimental waveforms of response of speed

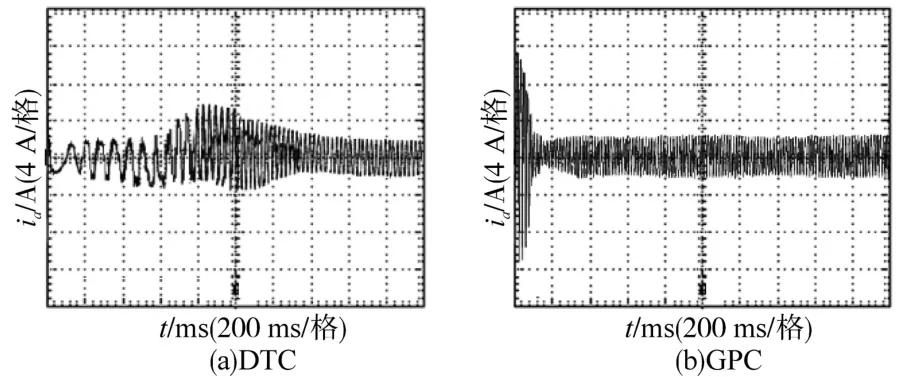
图11 电流响应实验波形Fig.11 Experimental waveforms of response of current

从图8中可以看出，GPC控制算法较DTC控制算法具有较好的动态性能，其达到稳态时间缩短了约40%。而在图9中可以看到，GPC控制算法产生的转矩脉动较小，达到稳态后输出的转矩稳态误差较DTC控制算法更小。

从图10中的转速响应实验波形可以发现，达到稳态后DTC控制算法的转速振动范围约为24 r/min（4/5格），而GPC控制算法产生的转速振动范围约6 r/min（1/5格），仅为前者的1/4。

图11电流响应实验波形同样反映了GPC控制算法较DTC控制算法具有较好的快速性和稳定性。

同时，为计算实验中DTC控制算法程序和GPC控制算法程序在DSP中的执行时间，在程序运行开始时将一个引脚置为高电平，退出时为低电平，并利用示波器进行观察。由于GPC控制算法在求解最优控制律时需要进行矩阵求逆，而且随着预测步长的提高，算法会变得复杂，增加了算法的复杂度，使得其控制算法应用受到了一定的限制，但这可以通过离散化等方法进行简化。实验中DTC控制算法执行时间约为112 μs，GPC控制算法执行时间约为148 μs。

实验结果说明了GPC控制算法虽然在DTC控制算法基础上增加了转矩预测的控制算法，但没有明显增加DSP的计算量，验证了该方法的有效性。

5 结论

从仿真结果及实验中可以看出，与DTC控制算法相比，GPC控制算法的磁链响应、电流的脉动明显降低，低速时的转矩脉动显著减小，输出转矩的稳态误差更小，而且保持了DTC响应迅速、控制简单的优点，在静态性能和动态性能两方面都体现出了较为明显的优势。