基于ANSYS的汽车轮毂优化设计

卢振生，陈宇佳，王艳玲，王迎辉，张全禹

(绥化学院，黑龙江 绥化152061)

随着汽车保有量不断地提升，截止2019年民用汽车拥有量25 376.38万辆，据国家统计局统计2018年用于交通运输、仓储和邮政业汽油消费总量达到2.2739亿t与2017年相比增加了3%[1].据《BP世界能源统计年鉴》的2019年度报告表明，以目前的石油消耗速度，石油只有不到50年的开采量[2]，作为燃油使用量最高的汽车已经成为了节能减排的研究对象，汽车的装备质量每减1%可节油1%～2%[3]，而镁合金具有密度低、抗冲击性好、抗压缩能力强、后续加工简单及可回收性高等多种优点，因此以镁合金汽车轮毂为研究对象，通过对其结构优化设计减小其质量，可提高汽车燃油经济性，从而降低能源的消耗速度.

1 轮毂模型设计及静力学仿真

1.1 轮毂模型的建立

本文所设计的轮毂以国家标准《乘用车轮辋规格系列》GB/T3487—2015为依据，针对AudiA6L车型的轮毂进行优化设计，轮毂参数如表1所示[4]，根据该参数，使用Solid work实体建模软件建立的轮毂模型如图1所示.

图1 轮毂实体模型Figure 1 Hub solid model

表1 镁合金AZ31B力学性能参数Table 1 Mechanical property parameters of magnesium alloy AZ31B

由于国家标准没有对左侧槽的侧边进行限制，为了避免使用直线后与两侧的圆角连接处出现应力集中的现象，所以本文采用了样条曲线对其进行过渡.

1.2 网格的划分

由于SOLID186号单元具有二次位移的特点，适用于不规则模型[5]，且其具有任意的空间取向，能够适应复杂的受力环境的特点[6]，而镁合金汽车轮毂模型沿轴线呈现出不规则形状，轮毂的圆周受非线性载荷，因此本文选择SOLID 186号单元作为网格划分单元，基于ANSYS自由网格对其进行单元划分，自由网格具有自动化程度高和操作简便的优势，本文选择自由网格对其进行网格控制[7].

将实体模型导入ANSYS软件中，在材料菜单中输入相应的力学性能参数，具体参数如表2所示[8]；通过网格划分控制器选择智能尺寸划分，精度等级为五级，网格划分结果如图2所示，划分的单元数为295 050个.

图2 轮毂网格划分Figure 2 Hub meshing

表2 轮毂参数Table 2 Wheel hub parameter

1.3 轮毂径向加载分析

为合理对汽车轮毂进行加载，本文依据汽车最大载荷计算公式可计算得到轮毂所受载荷，如式(1)所示[9].

(1)

其中：W为汽车自重取1 970 kg；G为汽车满载负荷取4 410 N；ni为载荷影响因素，本文取1.27.通过上式计算可得最大载荷Fmax为8 907 N.

将径向载荷Fmax通过函数编辑器加载至轮毂上，得到了径向载荷分布图像如图3所示.

图3 径向载荷施加图像Figure 3 Radial load application image

1.4 仿真结果分析

在汽车行驶时，轮毂作为直接与地面进行接触的运动部件，要承受车身向下的垂直载荷和来自路面不平带来的向上的冲击力，同时轮毂的使用环境较为复杂，难以判定在某个特殊情况下轮毂材料的特性[10]，防止轮毂在复杂的受力环境中破损失效，增加轮毂的使用寿命，在各方面达到轮毂所需的强度要求，本文选择对其各项应力进行分析，为计算汽车轮毂的应力分布和最大变形量出现的位置，选择直接求解器对其进行应力和最大形变分布求解，图4、5为根据第四强度畸变能理论计算得出的轮毂径向载荷背面von-Mises图和轮毂径向载荷正面von-Mises图.图6为根据第一强度理论计算得出的轮毂最大拉应力分布图.图7为根据第二强度理论计算得出的轮毂最大伸长线应变分布图.图8为根据第三强度最大切应力理论(Tresca屈服准则).图9为轮毂的最大形变量分布图.

图4 轮毂径向载荷背面von-Mises图Figure 4 Von-Mises diagram of hub radial load back

图5 轮毂径向载荷正面von-Mises图Figure 5 Front von-Mises diagram of hub radial load

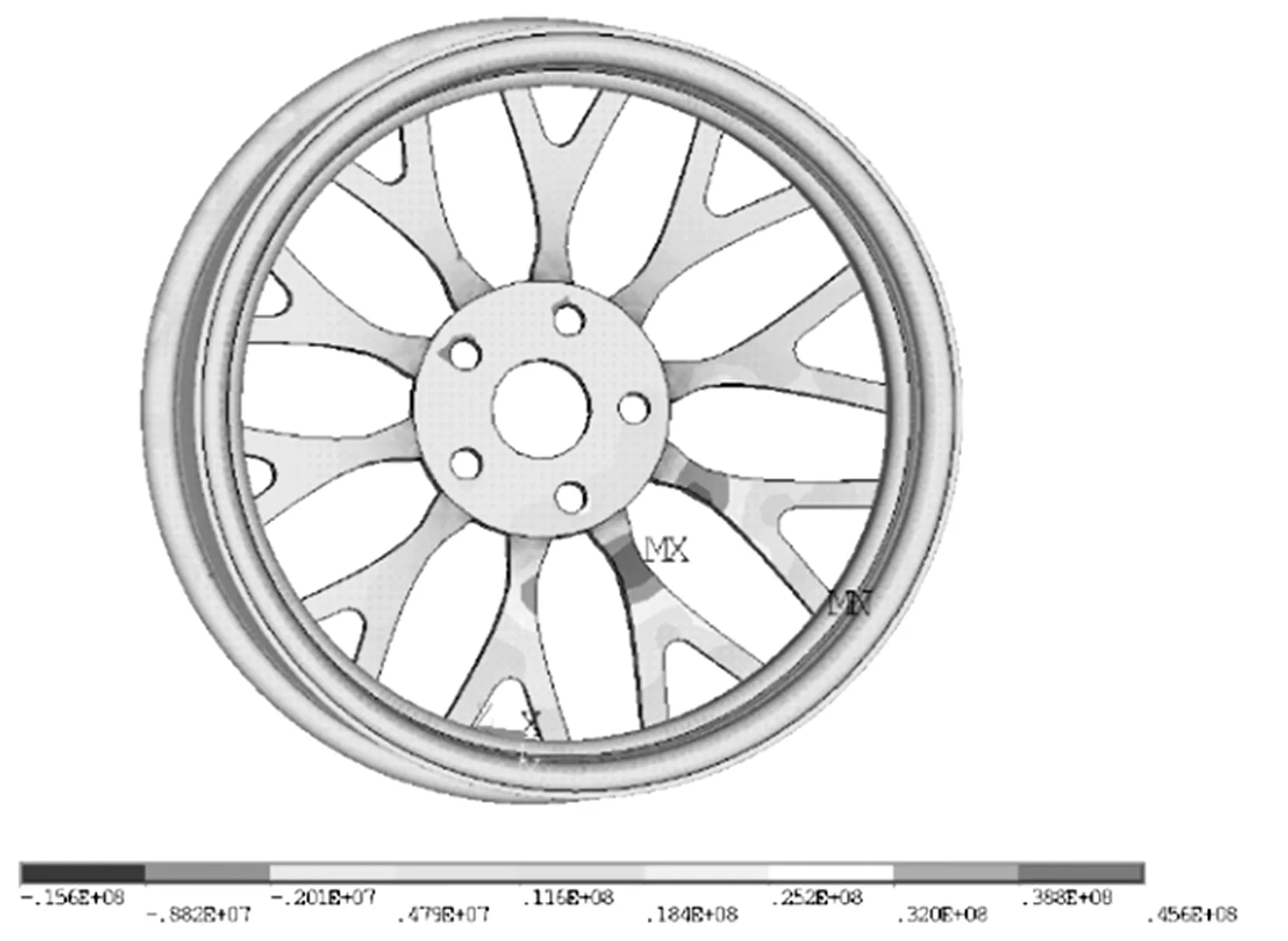
图6 轮毂最大拉应力分布图 Figure 6 Maximum tensile stress distribution of hub

图7 轮毂最大伸长线应变分布图Figure 7 Distribution diagram of maximum extension

图8 轮毂最大切应力分布图Figure 8 Maximum shear stress distribution of hub

图9 轮毂的最大形变量分布图Figure 9 Distribution diagram of maximum deformation of hub

由图4、5可以看出在承受径向载荷后，轮辐辐板正面和背面都出现了应力集中的情况，轮毂正面的最大应力为39.4 MPa，背面辐板处的最大应力达到了50.6 MPa，通过对比可知轮毂背面的挤压强于正面，这是因为在轮辐辐板正面呈现拱形突起，在承受载荷之后有向后弯曲的趋势，造成背部受到挤压产生了较大的应力，根据第四强度的畸变能理论，构件内任意一点的形状改变比能达到单项应力状态下的极限应力值，材料发生屈服破坏[11]，在安全系数为2.34时，轮毂的屈服强度最大为58.547 MPa[12]，通过图5、6可知最大应力并未超过镁合金的屈服强度，符合镁合金的力学性能.

由图6可知，轮毂的最大拉应力主要集中于轮辐辐板处，大小为45.6 MPa，在安全系数为2.34时，镁合金轮毂的极限抗拉强度为105.983 MPa，满足镁合金的力学性能，根据第一强度理论可知，材料破坏的主要因素是最大拉应力，当单方向上的周向拉应力达到临界值时裂纹出现并沿着最大拉应力的方向开始拓展，裂纹逐渐扩大直至材料断裂[13]，与第四强度畸变能理论不同，第一强度理论忽略了材料所受的剪切应力，在材料所受剪切应力较大或者多轴受载时就不能用拉应力来说明镁合金的破坏极限.

由图7可知由最大拉应变理论产生的应力为19.9 MPa小于拉应力的45.6 MPa、von-Mises等效应力的50.6 MPa，根据第二强度最大拉应变理论可知，当材料受载时，某一轴向载荷大于其余两方向的外部载荷时，材料承受大载荷方向所产生的损伤较多，导致该方向上承压能力大幅降低，当再次承受载荷时会升高该方向断裂的可能性，从图7可知此时的拉应力尚未达到镁合金的力学性能的极限，不会导致轮毂发生损伤[14].

由图8可知轮毂最大切应力也是集中于辐板靠近安装面的部位，而且最大切应力为16.3 MPa，说明此时轮毂容易因为径向的剪切在辐板处发生断裂失效的情况，且第三强度理论认为最大切应力是引起材料屈服的主要因素，无论何种应力状态，达到单向极限切应力材料将产生压缩破坏[15]，从图8可以看出此时的剪切应力未达到镁合金屈服强度，因此本文并未选择辐板进行加厚处理.

由图9可知轮毂的最大变形量在轮缘处，大小为1.282 mm，形变量较小满足刚度要求可以进行优化设计[16].

2 轮毂优化设计

将轮毂模型导入到ANSYS软件Workbench模块中，避免轮毂的外形发生改变，约束轮辋形状与轮辐安装面螺栓孔的轮廓为恒定，为使轮毂轻量化，以轮毂的整体质量为变量，得到轮毂质量随拓扑优化次数目标对象收敛图(质量收敛图)如图10所示.

图10 拓扑优化次数目标对象收敛图Figure 10 Topology optimization times target object convergence graph

由图10可知当优化次数超过38次以后轮毂优化结果基本收敛，即使次数再次增加对于优化结果来说没有任何的意义，只会增加计算机的计算量，增加优化时间；根据此种优化方式轮毂的结构变化图如图11所示为轮毂结构变化图，结构变化局部放大图.

图11 轮毂结构变化图Figure 11 Change diagram of hub structure

由图11可知，当轮毂质量保留85%，同时设定最大应力不超过100 MPa时，优化目标区域为汽车的轮辐安装面，所以本文对轮辐安装面的厚度进行了修改，图12为轮毂优化之后网格划分的结果.

图12 轮毂优化后的网格划分Figure 12 Mesh generation after hub optimization

为了进一步验证该优化结构的合理性，对其von-Mises、拉应力、线应变、切应力和形变量进行计算分析，如图13～17所示，分别为最大von-Mises、最大拉应力、最大伸长线应变、最大切应力和最大形变量的效果云图.

图13 轮毂径向载荷von-Mises图Figure 13 Von-Mises diagram of hub radial load

图14 轮毂最大拉应力分布图Figure 14 Maximum tensile stress distribution of hub

图15 轮毂最大伸长线应变分布图Figure 15 Distribution diagram of maximum extension linear

通过与图4～9的对比可以发现，轮毂的最大von-Mises应力减少了1.5 MPa，最大拉应力增加了12.9 MPa，最大伸长线应变产生的应力减少了0.5 MPa，最大切应力增加了0.6 MPa，最大形变量增加0.012 3 mm，由此可知变化最大的为拉应力，由于轮辐安装面的厚度减少，导致在螺栓处的作用面积减少，压力分布较为集中使得轮毂的拉压应力大幅度增加，达到58.5 MPa低于镁合金的屈服强度，符合其力学特性，由于其余几种应力变化幅度较小，不再进行分析，镁合金在常规条件下属于塑性材料，因此本文优先使用Tresca屈服准则和von-Mises准则对镁合金轮毂进行分析，通过图13和图16进行对比可知von-Mises应力大于切应力，为安全考虑本文采用von-Mises准则作为受力分析的强度准则，从图16可以看出最大von-Mises应力为49.1 MPa，小于镁合金的屈服强度极限；由图17可知轮毂形变量最大处为1.305 mm，形变较小可以忽略不计，最终优化后的轮毂质量为3.872 kg，质量小于目前量产的锻制镁合金轮毂的5.2 kg，优化效果较为明显[17].

图16 轮毂最大切应力分布图Figure 16 Maximum shear stress distribution of hub strain of hub

图17 轮毂的最大形变量分布图Figure 17 Distribution diagram of maximum deformation of hub

3 结 语

镁合金作为一种新型材料能够有效的减轻产品的质量，如果能够对于汽车上的一些厚重的零件进行材料的改进能够有效的减轻汽车的总体质量，同时大幅度的提高汽车的燃油经济性.相比于铝合金和铸铁来说，镁合金不仅密度较低，而且因其较高的阻尼系数能够大幅度减少汽车运动时带来的噪声和震动，可以提高驾驶员的舒适性，减轻长时间驾驶带来的疲惫感，

相较于铝合金来说镁合金还拥有更加优良的加工性，在相同的加工条件和设备下，镁合金的生产成本和生产效率都要明显的优于铝合金，所以能够为生产商带来更多的收益.但镁合金也有自身的缺陷，作为活泼金属镁合金的耐腐蚀性不如铝合金，如何通过提高镁合金中其他材料的占比提升镁合金耐腐蚀性成为目前的主要问题.因为汽车轮毂经常工作在恶劣的环境中，如果没有良好的耐腐蚀性经过长时间的化学反应会导致其失去原本的性能，一旦出现性能缺陷就会给驾驶员带来巨大的风险.