复杂环境下的WIFI室内定位算法研究

王 琦，席志红

(哈尔滨工程大学 信息与通信工程学院 先进船舶通信与信息技术工业和信息化部重点实验室，哈尔滨 150001)

进入21世纪，科技水平不断发展进步,极大地促进大众生活水平显著提高，定位技术一经推出就受到市场广泛的欢迎，促进了定位服务的市场需求的产生.基于位置服务LBS[1](location Base Services)受到各行各业需求日益增大.目前定位主要划分为如下：室外定位与室内定位，对于室外定位，全球卫星导航系统GNSS(Gobal Navigation Satellite)[2]完全可以提供较高精度定位结果，例如：我国北斗系统[3]以及俄罗斯的格洛纳斯[4]系统等均是较为成熟系统在军民领域均有广泛应用，卫星导航室外定位系统如图1.

图1 卫星导航室外定位系统示意图Figure 1 Schematic diagram of a satellite navigation outdoor positioning system

但将其应用于室内定位就会出现较高误差以及不适用复杂空间环境等问题，究其主要原因是建筑物墙体以及室内环境中各类物体等遮挡的影响，卫星信号的衰落非常明显，使得定位的误差巨大而无法达到较好的定位效果,多层商场的定位如图2.

图2 商场室内定位示意图Figure 2 Schematic diagram of indoor positioning of shopping malls

目前对于室内定位技术包含有以下：射频识别定位技术[5]、超声波定位技术[6]、可见光定位技术[7]、超宽带定位技术[8]、蓝牙的定位技术[9]、红外线定位技术[10]以及WIFI定位技术[11]等.基于WIFI的定位是目前室内定位最具有发展前景的定位技术,基于WIFI的定位系统依赖硬件WIFI路由器设施以及智能手机就可以实现定位，这无疑使得WIFI的定位技术在商业广泛应用以及普及具有巨大的潜力.但是室内定位环境复杂多变，在实际的环境中非视距(Non-Line of Sight , NLOS)[12]以及其他类干扰会严重影响WIFI信号在室内空间的无线传播，这种影响会导致定位的参数严重偏离真实值，进而导致算法的定位性能大幅度下降.

目前对于WIFI定位下的非视距干扰问题提出很多方法：1)首先依靠定位信息对于卡尔曼滤波器的增益进行调整[13]，以此来滤除NLOS误差，但对于卡尔曼滤波中的参数无法自适应的调整；2)针对测距中的NLOS误差，将TOA值和NLOS误差值作为卡尔曼滤波的2个状态向量直接估计出NLOS误差[14]，该算法计算复杂度较低，但由于某些特定的环境中模型系数无法确定所得到的NLOS误差并不满足实际定位；3)选择代表性的测量样本的标准差和测量噪声的标准差鉴别NLOS误差，提高测量精度[15]，但这种方法引入了时间延迟，较复杂而且不能进行实时定位；4)采用偏移卡尔曼滤波处理测量数据[16]，将非视距误差视为服从指数分布的，但将测量噪声的均值加入到卡尔曼滤波计算中，这种做法需要大量实验数据且不具有代表性，不能适用于任意非视距环境.

本文对于现有扩展卡尔曼滤波技术进行改进，将实际观测值与测值做差.同时设置阈值与相应的差值进行比较，以判定定位环境是否为视距/非视距并改进扩展卡尔曼滤波迭代过程.同时对于为了防止判定的不准确，加入路径损耗模型实现对NLOS误差的粗略估计，加入扩展卡尔曼的距离滤波模型做进一步估计，进而以此估计值对定位结果进行改正.利用改进后的扩展卡尔曼滤波算法消除非视距误差和噪声对定位的影响，实现了更准确的室内定位.

1 室内复杂环境对WIFI定位影响

1.1 WIFI传播影响因素

由于本文所定位环境干扰因素较多，WIFI信号强度在空间内易受到干扰而产生的波动不稳定，具体影响WIFI不稳定的因素有以下几种[17]:

1)室内空间人员活动

室内空间的人员流动会对传播过程中的WIFI信号产生反射和折射，导致WIFI信号在传播过程产生衰减，会使得WIFI的数值不稳定.因为人体在室内活动的多变性以及随机性比较大，没有固定模型去描述人员对于信号影响规律.

2)WIFI传播多径效应

基于WIFI的室内定位处于复杂空间时就会有多径效应的产生，主要由于WIFI信号在空间中的传播可以采用多条路线到达WIFI信号的硬件接收设备，对于室内空间一般存在复杂的结构，会因为外在干扰使得最终的WIFI信号到达硬件接收设备不同时间，存在一定时间差值，最终得到WIFI信号不稳定会出现峰值与谷值相互叠加不稳定.WIFI传播的多径效应示意图见图3.

图3 多径效应示意图Figure 3 Schematic of the multipath effect

3)同环境私人AP影响

由于WIFI设备的普及，在教学楼内存在多种多样的AP设备，必然会对于WIFI信息采集产生干扰，当今大多数无线WIFI设备的标准是IEEE 802.11 g/n的2.4GHz频段.这些私人AP设备会对WIFI信号产生干扰，使测得的RSSI数值不稳定，在测量点的值出现很大的误差.

1.2 WIFI信号RSSI值得随时间的波动性质

选取AP1、AP2在某段时间内连续200次、500次的RSSI数值进行统计分析：

通过分析图4、5可以看出，AP1、AP2在这个区间内大致波动的范围为-68、-69 dB为均值上下波动.也可以看出在某些时刻的曲线会出现巨幅的波动，使得当时刻所测量的RSSI值偏离均值中心.上述影响因素主要由于室内空间环境多径效应影响.凸起的部分主要可能对于WIFI信号经由不同路径到接收端正好波峰，出现了波峰相互叠加：凹陷的部分可能是信号传输至接收端正好波谷，出现了波谷相互叠加.

图4 同一位置采样200测序RSSI值变化Figure 4 Sample 200 sequencing RSSI values at the same location to change

1.3 WIFI信号的RSSI值一天动态变化

为了研究WIFI信号一天之中的变化，本文对于同一位置的AP节点进行24 h监测其信号变换规律.选取相应的AP的信号强度24 h内的动态数值变化如图6所示.

从图6看出，RSSI测量值的均值按照从大到小依次排布为: AP3, AP2, AP1, AP4，AP6, AP5.与此同时也可以发现对于整体的AP的RSSI数值均值上下波动不时很大，仅围绕着一个中心上下波动.

图6 AP一天内数值变化Figure 6 The AP values change within a day

结合实际的采集环境的情况可知，在学生下课以及老师下班以后的时间段(23∶00～8∶00)时，这个区间内的信号强度数值相对稳定，没有很大的起伏波动.从9∶00～22∶00，对各个 AP的信号强度出现较强幅度变化，主要原因是人员流动性比较大，对于WIFI信号的干扰比较大.由此可以看出，采集过程中人员的流动对于AP的信号强度数值影响比较显著.

1.4 基于空间的WIFI信号研究

在室内定位空间内，通过采集设备获取信号强度值，随机选择一个位置，朝向远离AP3方向行进，此过程保持一个直线行进路线.间隔1米测量AP3的RSSI值，本文共测量15次数值，通过实验得出AP3的RSSI值与距离之间的关系如图7所示.

图7 RSSI与距离之间的变换图像Figure 7 The rollover image between RSSI and distance

整体可以看出，AP3的数值在总体趋势上随着距离增大而减小，符合路径损耗模型，但是值得注意的是整体过程部分结果可能出现波动，主要原因可能室内空间人员的流动、室内的私人AP设备同频段的干扰以及内复杂的环境导致出现多径效应，导致在部分位置上出现了波动.虽然会出现一些突变不稳定的情况，但对于 WIFI的信号强度会随着距离的增大整体减小的趋势.

1.5 WIFI信号的RSSI的预处理

通过对于上述分析，为了保证定位结果准确性和稳定性，无论是对于离线位置指纹，还是对于实时性测定的RSSI，在定位时均需要多次进行信息的采集，特别对离线指纹库的建立所要存储指纹信息.由于RSSI的数值无论在时间以及空间RSSI均可能由于环境的干扰产生变化，存在一定的波动性.因此在室内定位进行之前需要对于采集到的RSSI值进行预处理，通过预处理手段可以有效避免随机性干扰对于实时性的定位的结果产生干扰.常见的滤波方法有均值滤波、高斯滤波.本文采用改进高斯滤波技术对于RSSI值进行预处理[18].

RSSI服从(0,μ2)，其概率密度公式如下：

(1)

其中

(2)

(3)

其中：F(RSSI)表示为概率密度;μ代表均值;σ2代表方差.

针对因为噪声等因素干扰而对于WIFI的RSSI值产生的波动，本文对于传统的高斯滤波进行改进，具体如下：

1)输入采集样本值.为了避免噪声的干扰，在进行信息采集时应当进行多次采集.

2)高斯滤波.对于第一部分的样本值引入高斯模型滤波处理.选取概率空间为90%内的.

3)小概率样本值处理.通过高斯滤波技术可以有效的对于小概率空间的样本值进行剔除，设置小概率空间的集合为W，集合空间内的样本值为k，则：

W=[RSSIout1,RSSIout2,…,RSSIoutk]

(4)

对于集合空间内的样本值进行赋值，公式如下：

(5)

其中：RSSIoutj为W中数据.

4)输出结果降噪:通过进行滤波技术将小概率空间的数据赋值后，通过样本选取标准将其汇入大概率空间的样本数据中，最终保存在离线指纹库中.

2 滤波算法

2.1 扩展卡尔曼滤波算法

传统的卡尔曼滤波技术仅适用于理想高斯的线性空间，卡尔曼滤波只有在线性系统中才能有很好的跟踪效果，然而在实际的室内定位环境大部分为非线性，观测方程等各种信息无法用线性表示.所以对于传统的卡尔曼滤波进行改进，以便于在非线性空间也可进行滤波定位，对于卡尔曼滤波技术改进应用最为广泛的是扩展卡尔曼滤波(Extended Kalman filter，EKF)算法[19].扩展卡卡尔曼滤波技术是将数学期望进行线性化的KF算法.EKF算法对于传统的KF算法进行补充，以便其适用于非线性系统的室内定位中，扩展卡尔曼滤波技术是将数学期望进行线性化的KF算法.EKF算法对于传统的KF算法进行补充，以便其适用于非线性系统的室内定位中.

设定系统的状态方程如下：

Xk=Axk-1+Buk-1+ωk-1

(6)

其中：X为状态向量；A为转换矩阵且其维数为n·n阶；B为转换矩阵；ω为系统噪声输入.

当测量值为Z，则测量值和状态值之间的关系为：

Zk=HXk+vk

(7)

(8)

系统的噪声为高斯白噪声，则其方差为：

E(w(k)vT(j))=Q(k)δkj

(9)

E(w(k)wT(j))=R(k)δkj

(10)

设定这里v(k)和w(k)是不相关的则：

E(v(k)wT(k))=0

(11)

对式(8)进行泰勒级数展开得到进一步预测值即：

其中：fk代表状态模型，

(13)

(14)

(15)

其中：Fx(Xk)为中心点的雅克比矩阵.对(12)所展开的泰勒级数进行一阶截取可以得

(16)

则一阶的泰勒展开式的数学期望为：

(17)

一阶的泰勒级数展开得方差为：

(18)

因此由式(16)～(18)构成扩展卡尔曼滤波基本算法.

对扩展卡尔曼滤波算法基本步骤总结：

1)对状态方程和测量方程初始化，即k=1时：

(19)

(20)

2)对于进行初始化的状态量进行线性处理：

(21)

3)对于系统的状态向量、误差以及协方差进一步预测，同时对于量测方程也进一步预测得：

(22)

(23)

Zk+1=hk(Xk+1)

(24)

4)对量测向量线性处理得：

(25)

通过测量线性化处理，进一步更新状态估计值与误差值：

(26)

(27)

因此当(k+1)→1，则返回步骤(2)进行状态估计更新

2.2 算法局限性

通过上述分析可以看出与传统卡尔曼滤波算法，扩展卡尔曼滤波技术在非线性空间上有更好的适用性，通过文献以及理论研究发现对于EKF算法在实现室内定位时也是存在一定的局限性：

1)EKF算法对于非线性的函数进行线性处理得到相应的近似函数，EKF是滤波算法是对于泰勒展开式进行一阶截取，而忽略高阶项，虽然一定程度使得EKF算法适用于非线性中，但是同时也会伴随滤波精度不高甚至对于复杂的空间形式可能出现定位不稳定性或者导致滤波结果发散.

2)扩展卡尔曼滤波技术的计算复杂度较高、计算量大、错误率高、实时性低，当进行线性化处理后数值不稳定时，就会难以找到非线性函数的雅克比矩阵.

3)扩展卡尔曼滤波算法的状态与测量函数需要是连续可微的.

3 算法改进

3.1 阈值设定

对于本文所研究复杂空间的室内环境下，存在各类的因素干扰，这些因素均会对WIFI信号强度RSSI造成干扰，最终导致在复杂空间内的NLOS定位误差.因此本文对于现有扩展卡尔曼滤波技术进行改进，将实际观测值与测值做差.当差值小于等于阈值，判定为定位环境是处于是LOS 场景下的，同时对于EKF算法的滤波增益不作改变; 反之表明此时的定位环境为NLOS环境下的并且存在NLOS 误差，将EKF的滤波增益设为0，则：

(28)

(29)

对于阈值为在进行室内空间的定位时所设定.根据对于误差与阈值判定的结果此时对状态方程和误差进行更新.运动过程中，由于某些位置遮挡严重，通过设置阈值范围，超出阈值范围用卡尔曼滤波的状态估计值代替，避免了误差过大的测量值定位结果的影响.可使定位结果更加准确可靠.

3.2 误差分析

考虑设备响应时间有延迟产生的误差.标准时间偏差和NLOS误差的存在是影响WIFI定位精度的主要原因， 标准时间偏差产生的误差除硬件本身产生的误差之外，还 包 括 温 度 等 各 种 外 界 条 件 的 影响，其改正模型为：

dSD=cn+μ(s)+wn

(30)

其中：cn表示由固定时延误差，硬件设备的误差、非同时启动误差和温度等外界条件产生的误差.

根据以上模型可以发现，由于不同设备存在的偏差不同，因此需要对每个设备进行测试.假设温度、湿度和大气压等外界条件不变，在不存在障碍，改进的方法测出的距离信息精度较高；NLOS情形下，路劲损耗在传播过程中墙体、桌椅等各种障碍物的介入产生了附加时延，是非视距条件下的测距误差的主要来源.在LOS情形下，由于DP传播过程中不存在.

3.3 定位干扰因素的处理

本文对各项误差判断方法，通过阈值判断，在量测信息正常时，直接通过WIFI定位模型融合扩展卡尔曼距离滤波器进行解算，在量测信息出现异常时，通过扩展卡尔曼距离滤波器去除噪声，在完全NLOS条件下，首先通过路径损耗模型对距离进行修正，通过路径损耗模型进行修正之后的距离值 ：

(31)

以此距离值作为最终的距离值得出最终的定位信息.

4 实验与仿真分析

4.1 实验环境搭建及其样本采集

本文实验地点为某教学楼走廊部分，对于实验区域内WIFI信号已经全覆盖，如图8所示某教学楼实验环境，本文应用华为手机及传感器进行WIFI信息的采集，在空间内均匀布置6个AP发送设备.对于AP的SSID用于区分同一区域所接受的WIFI信号强度.实验环境被分割为1米的网路结构，对设备进行信息采集.实验过程中人员走动不受限制.

图8 某教学楼实验环境Figure 8 Experimental environment of a teaching building

本文同时对于WIFI信号进行采集分析，采集AP的设备为飞行堡垒7代电脑，笔记本外设驱动进行修订，同时也采集30个子载波带组的信道矩阵，通过该方式可以很好的识别以及抑制复杂空间的WIFI信号的多径效应

但考虑到对实际情况的考虑，为了具有普遍性采用易于获取的RSSI，采集WIFI信号强度RSSI才用的是利用手机软WIFI Scan采集当前参考点处的离线指纹数据，对于发送硬件AP设备主要是H3C 、TP-LINK 、XIAOMI,该软件的数据采集界面图如图9所示.

图9 WIFI采集软件界面Figure 9 WIFI acquisition software interface

对于在每个RP采集RSS信号强度时，由于人员在实验环境中测量时会干扰信号强度，所以采集数据时要需要在每一个RP分别采集东南西北四个方向的信号强度.

4.2 基于改进算法的定位仿真分析

扩展卡尔曼滤波算法对于处理本文所要实现的在复杂空间的定位情况，相对于传统的KF、EKF算法相对于可以达到较为高精度的定位结果.下面对于改进的EKF算法在NLOS情况下仿真实验.

(32)

其中：ft为目标的动力，Δt为进行扩展卡尔曼滤波的采样间隔.假设物体在第一阶段教室内走廊进行直线的匀加速直线运动，然后一个简单的转弯动作，最后在进行匀速直线运动.在上述的运动情况下进行复杂空间的NLOS的定位跟踪技术研究.过程噪声方差Q=2，测量噪声方差R=10，采样间隔为1 s，采样时长为100 s.使用EKF算法对于NLOS环境下进行室内跟踪定位，在所处走廊匀速以及拐弯处的误差，仿真如图10～13所示.

图10 基于EKF以及改进算法仿真Figure 10 Based on EKF and improved algorithm simulation

图11 匀加速直线走廊运动定位误差Figure 11 Uniform acceleration linear corridor motion positioning error

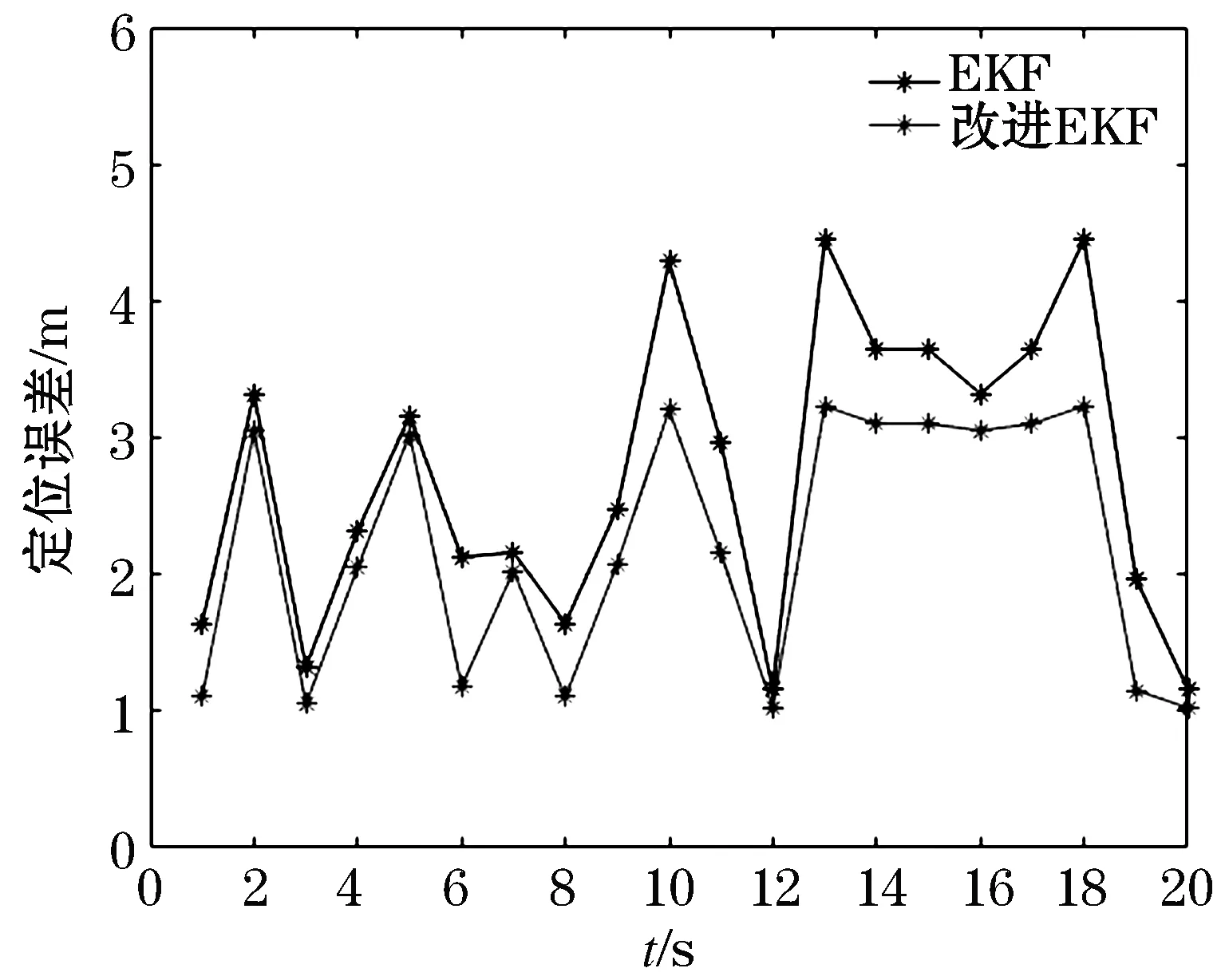
图12 在拐弯处的定位误差Figure 12 Positioning error at the bend

图13 两种误差累积曲线Figure 13 Two error accumulation curves

通过上述仿真可以了解到，对于传统的EKF与改进算法在LOS环境下的定位误差相对差别不大，起始点处由于获取的定位信息相对较少，扩展卡尔曼滤波算法对于目标跟踪的定位的可信度出现误差，在后续的定位中，基本误差定位稳定在1～2 m之间具有较好的跟踪定位效果.但是处于NLOS环境时，在拐角处进行定位时，由于各类多径干扰、拐点处AP节点像话干扰等多重干扰因素较多导致定位误差较大，可以看出对于现有EKF算法改机处于拐角处的定位误差明显下降.证明该算法具有一定的定位效果.但是由于误差较大，对于室内定位技术还是存在一定精度上改进需求.

5 结 语

本文基于改进的EKF算法，得到了定位的观测值.通过建立“当前”统计模型，利用改进扩展卡尔曼滤波算法得到了更为准确的标签位置，减少了 NLOS 误差和噪声等因素对定位结果的影响.实验发现，滤波算法能较好地跟踪目标的运动，有效提高了定位的精度.