基于核心素养的定积分单元教学设计

◎赵晨如 王淑芬 (新疆石河子大学，新疆 石河子 83000)

2016年吕世虎教授等人发表的《数学单元教学设计的内涵、特征以及基本操作步骤》一文中强调了数学单元教学设计必须站在提升学生核心素养的角度上；2016年钟启泉教授在《基于核心素养的课程发展：挑战与课题》一文中指出“核心素养—课程标准—单元设计—课时计划”是环环相扣的教师教育活动的基本环节；2017年喻平在《发展学生学科核心素养的教学目标与策略》一文中给出一系列教学策略；《普通高中数学课程标准(2017年版)》中明确提出要着力发展学生的数学核心素养.

数学单元教学设计具体来说就是以培养学生数学核心素养为目标，综合性、深入性地研究教材内容，全面性、系统性地分析知识的关联性，有针对性地选择讲授主线，将教学内容进行再组织、设计、优化之后，形成一个更符合学生认知规律、数学知识体系的新整体.在单元教学设计中研究主线的精确选择是保证后续教学设计及教学效果的关键，本文以数学文化渗透为单元设计研究主线，从微积分的实际问题起源出发，通过定积分案例开展分析，从中体现学生的数学核心素养.

一、分析单元内容，对标核心素养

定积分这一单元是高中数学选修2-2中第一章“导数及其应用”的内容，在变化率及导数的相关知识之后进行学习，主要包含曲边梯形面积求解、变速运动的路程求解、概念产生、公式运用等.这一部分内容既包含了问题、概念、应用，又涉及数学史、数学符号、数学美等数学文化，可以很好地落实六大核心素养.

要完成本单元的教学目标，教师要系统熟悉微积分发展史的历程，并以此为基础梳理知识框架，构建微积分思维导图，使其内容按照历史发展顺序整体呈现学生眼前，这样可达到事半功倍的效果.如表1是按照数学发展顺序对知识点的分析.

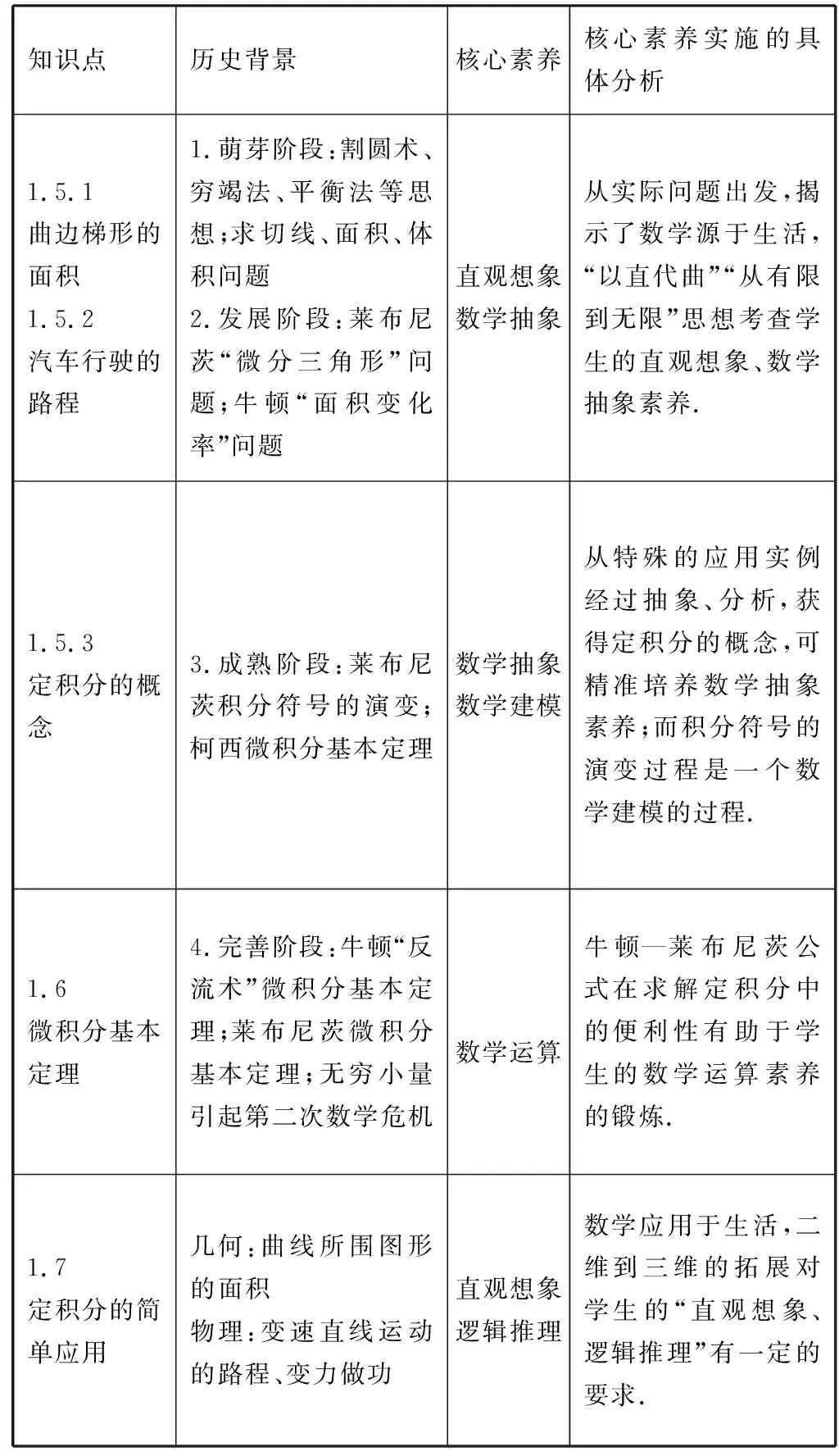
表1：相关知识点分析

这一单元内容从整体把握定积分相关知识，将数学史穿成一条线，这样有助于学生理解“微积分从哪来、怎么用、在哪里用”等问题，促进学生的数学核心素养的培养.

二、分析教学要素，研究教学策略

俗话说“磨刀不误砍柴工”，因此，我们要做好单元教学设计，就必须对影响教学效果的各教学要素的整体性、关联性、发展性进行详细分析.本文整体把控了单元内容,明晰了课程标准，全方位汲取了各版本教材的优点，充分了解了学生的已有知识水平、认知规律等，精准把握了单元内容的重难点.

(一)教学要素分析

1.学科分析

微积分的创立在数学发展史上具有里程碑的意义，牛顿—莱布尼兹公式将看似无关的导数与定积分完美地联系在一起，架起了数学与物理两大学科间的桥梁，很好地体现了数学的应用价值.

高中阶段定积分单元的内容也是后续高等数学要继续深入学习的重要内容.该单元作为培养学生从数学“初等有限思维”到“高等无限逼近”的入门篇，在学生整个数学学习能力的螺旋上升过程中起着举足轻重的作用，对于培养学生用动态的数学眼光“思考问题、分析问题、提出解决方案、抽象数学共性、建立数学模型”更是意义非凡.这恰好体现了课标中要求的“数学抽象、直观想象、数学建模、数学运算、逻辑推理”等数学核心素养.

2.课标分析

2017版新课标对微积分的教学提出了更高要求.首先，微积分这一内容设置在选择性必修模块，以强调其重要性.其次，注重与高等数学接轨，使课程更具连贯性；对连续函数给出明确的定义，注重对数学符号语言的培养；强调借助几何直观和物理情境引入微积分思想，对实际应用能力提出更高的要求；此外，新课标明确要求学生要对微积分发展史有清晰的了解.

3.教材分析

不同版本的教材对“定积分”单元编写均是按照“具体实例—抽象概念—实际应用”的模式呈现的，体现了从具体到抽象再到具体的思想方法.但是不同版本在“曲边梯形的面积”和“汽车行驶的路程”求解过程的呈现方式不同，在应用部分的拓展也有一定区别.

(1)引入部分

人教版教材对上述两个问题进行具体分析并提出思考，清晰地呈现“分割、近似、求和、取极限”四个步骤，更关注概念形成，突出了“以直代曲”“有限到无限”“逼近”的思想，通过归纳分析得出定积分的概念.

北师大版类似于数学解题，直接划分区间求和，方法步骤极为简便，没有体现微积分思想.

(2)应用部分

人教版在“定积分的简单应用”部分介绍了几何和物理两个方面；而北师大版介绍了平面图形和几何体体积的应用，考查了学生的直观想象素养，虽然从二维到三维跨度较大，但是有利于提高学生思维水平，同时与高等数学衔接得更好.

4.学情分析

学生通过学习导数及其应用的相关内容，对“极限”思想有了一定了解.这一部分内容对学生的抽象思维水平要求较高，学生难以将有限延伸到无限，教学过程中教师要考虑到学生的思维水平和认知规律，不断引导学生在类比、归纳和总结过程中掌握定积分这一单元的知识点.

5.重难点分析

本单元是一个全新的起点，运用“分割、近似、求和、取极限”思想解决曲边梯形的面积及变速运动的路程问题,较难理解，同时定积分的概念具有抽象性，既是重点也是难点.重点是理解定积分的几何意义，能够运用牛顿—莱布尼茨公式进行简单的定积分计算，其中蕴含的“极限”“以直代曲”“有限到无限”等思想是一大难点.

(二)选择教学策略

1.工具化策略

借助多媒体辅助教学，几何画板演示刘徽的割圆术，有限到无限分割让学生直观观察，通过已有知识并借助几何图形直观想象感知事物的形态与变化.

2.问题探究策略

问题探究是通过一系列的问题思考、分析、探究等方式发现知识，通过不断提出问题引导学生思考，发散学生的思维.

3.纵向对比策略

纵向对比是对不同历史阶段的定积分符号对比分析，通过比较各种符号的特点，体会数学美，并理解定积分的几何意义.

4.主体启发策略

引导启发学生，激发学生的思维，从平面面积到立体体积的拓展，让学生的思维从二维空间上升到三维空间，从而培养学生的直观想象的核心素养.

三、确定教学目标，选择教学方式

教学目标是教学的方向，教学设计的核心工作，引领着整个教学.教师通过分析课程标准并结合微积分史，以“历史发展”的视角构建“定积分”单元，整体把握单元目标及章节目标，并通过这些目标选择合适的教学方式.教学目标及方式如表2：

表2 教学目标及方式

四、顺承知识逻辑，设计教学片段

通过上述对教材、内容、目标等分析，教师对部分教学片段进行设计，分别从数学史、数学问题、数学美、数学拓展几个方面探究.

(一)“溯源式”案例(教师为主)：

1.教学目标：通过“割圆术”“曲边梯形面积求解”“变速直线运动的路程求解”等例子的分析，使学生掌握定积分的思想.

2.教学策略及手段：①借助几何画板的直观性演示刘徽的“割圆术”，使学生直观感受无限逼近的过程，感受数学的魅力与数学家的智慧.②追溯微积分的发展源头，让学生明白抽象数学概念的来源是离不开实际应用的，不是“无源之水”.

3.教学方式：直观演示、启发引导、问题讲解

4.教学过程

师：同学们，你们听过“割圆术”吗？

生回答.

师：“割之弥细，所失弥少；割之又割，以至于不可割，则与圆合体，而无所失矣.”这句话有谁知道是什么意思？

生5秒思考.

师：下面我们一起通过几何画板来直观感受一下这句话的本质.

活动：展示几何画板.

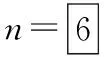
n-1=5.00

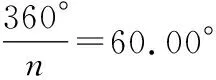
n-1=11.00

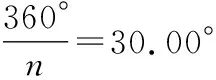
师：如果边数n不断变大，会是什么情况呢？

生5秒思考，师提问1-2人.

师(拓展)：伟大的数学家刘徽算到圆的正3072边形时，正多边形的面积已经非常接近圆的面积了，当边数继续增大时，两者的差距就会继续缩小，越来越接近零.

师(凝练)：这个例子中的用已知正多边形来逼近圆的思想非常重要.

师(总结)：“割圆术”中蕴含的用已知多边形来逼近圆的数学思想就是我们这节课重点来探讨的核心思想.

师(追溯)：17世纪伟大数学家牛顿解决物理上的运动问题及莱布尼兹在解决“微分三角形”的问题时都揭示了积分思想的萌芽.

师(回归)：当跳出物理和几何背景后发展成熟的定积分思想在社会发展中起着重要的作用，更是为物理和几何的应用提供了强有力的支撑.

(二)“探究式”案例(学生为主)：定积分概念的讲解

1.教学目标：引导学生探究归纳不同问题的共有属性，深入分析后，教师给出抽象的定积分概念，另通过直观几何意义使学生加深对概念的理解.

2.教学策略及手段：设置一系列递进问题，创设问题情境，用类比的方法培养学生的问题意识，激发学生的好奇心和求知欲，培养创新思维.

3.教学方式：问题探究、小组讨论、启发引导

4.教学过程

知识前提：师生已经完成曲边梯形面积和变速直线运动路程的求解过程分析.

问题1：对比曲边梯形面积和变速直线运动路程的求解过程你发现什么规律？

问题2：对于更一般的曲边图形的面积能不能用“四部曲”(如图1所示)？

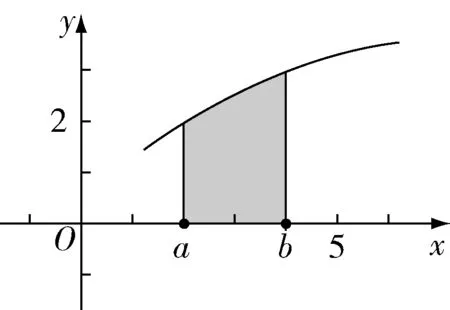
图1 曲边图形

问题3：类比区间[0，1]的分割完成区间[a，b]的n个小区间分割，写出小区间长度的表示，思考是否必须等分.

问题4：类比例题的取值完成每个小区间上的取值，思考取值中的点ξi的任意性.

问题5:小组探讨f(ξi)Δxi在具体问题中的意义.

问题7：通过极限体现无限逼近的过程.

问题8：总结“分割、近似、求和、取极限”这一过程的分析.

探究总结：通过抽象概念的分步分层拆解及问题思考探究，帮助学生理解抽象的数学概念.

(三)“赏析式”案例：定积分符号的讲解

1.教学目标：让学生了解数学符号产生背后精彩的历史，感受数学美；培养学生感受美、欣赏美、创造美的能力.

2.教学策略及手段：创设数学符号史情境，让学生置身于此情境经历数学符号的演变历程；通过趣味翻译，感受不一样的符号美.

3.教学方式：情境教学、对比分析

4.教学过程：

师：在了解积分符号的国外演变过程后，大家一定很好奇我们国家是什么情况，数学家李善兰在1859年翻译了第一本微积分教科书《代微积拾级》,下表是数学符号在当时的表示形式.

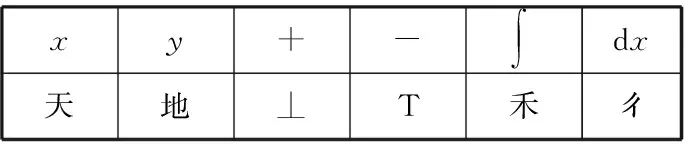
xy+-∫dx天地⊥T禾ㄔ

生1：“禾二天ㄔ”.

生2：“禾天二ㄔ”.

师：同学们翻译得很棒，这样的表示体现了我国当时微积分的发展特色，但显然这样的书写烦琐难懂，具有一定的局限性.

(四)“拓展式”案例：(开放作业)平面图形面积到旋转体体积的拓展

教学目标：在已学知识的基础上延伸新的知识，将二维拓展到三维，培养学生的直观想象、逻辑推理的数学核心素养.

我们已经会用定积分解决面积问题，那么三维空间求体积能不能用定积分来解决？下面是一个圆锥体积的问题，课后思考探索.

题目：给定一条直角边为1的等腰直角三角形(如图3)，绕一条直角边所在直线旋转一周，得到一个圆锥体，求其体积.如何利用“分割、近似、求和、取极限”这一过程计算？

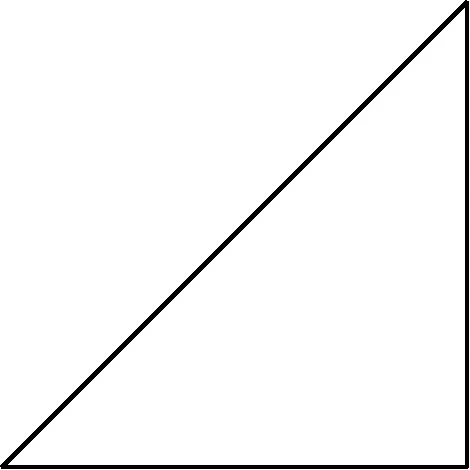
图3 等腰直角三角形

五、结 语

定积分单元教学内容虽是高中数学的选修内容，但作为数学大厦中至关重要的部分，对于培养高中生螺旋上升的数学知识非常关键，可很好地满足个人数学能力发展及社会进步.但本单元讲授内容涉及面广泛、教学课时相对偏少、与前期知识关联度较低，因此，学生学习效果往往不尽如人意.在大力推进新课改、着力培养学生数学核心素养、聚焦学生为课堂主人的教育大背景下，教师就需要在教学过程中积极探索新模式、新策略、新技术，激发学生学习的主观能动性，辅以自己系统性、引导性、探究性的教学设计，真正意义上实现课堂教学中师生一体化协同学习模式.单元教学设计是培养学生核心素养的一个重要途径，新教材和课标都体现了单元教学设计.从数学史出发进行设计，可以让学生了解微积分的来龙去脉.教师通过各类教学方式加以适当教学策略完成多元化案例设计，开展单元教学，整体把控定积分模块教学，这样使数学知识更具系统性、连贯性.