TPACK框架下的深度学习——以“导数的几何意义”为例

◎陈漪棋 (华南师范大学数学科学学院,广东 广州 510631)

TPACK为教师这一传统行业的素质提升与教学发展水平的提高提供了新的视角.在课堂教学实践中，教师要想有效地使用技术，就必须明确信息技术在何处、如何以及为什么要整合信息技术，理解信息技术与学科内容、教学方法之间的相互关系.基于此，本文将深度学习与TPACK框架进行结合，对“导数的几何意义”进行教学设计，将两者的优点融入教学中，使学生能够更好地体验学习过程，理解并掌握新知.

1 深度学习与TPACK框架

随着高速发展的信息技术在教育领域的广泛应用，教师将技术和教学内容知识融入课堂.这样在丰富了传统的育人教书的方法基础上提升了课堂中的教学方法，有助于教师高效完整地完成教学任务.数字化教育资源可以帮助教师通过新的方法实践、特权可及性、全纳教育、参与学习和知识构建来丰富他们的课堂.深度学习这里所谓的“深度”，是指学生的深度学习.在素质教育推行的背景下，如何促进学生深度学习正在成为越来越重要的课题，这也使得深度学习有了更高层面的理解：通过知识的学习，学生的核心素养得到发展，学生成为全面发展的人.

美国学者Mishra与Koehler于2005年提出了整合技术的学科知识框架这一理念.TPACK框架在最底层包含三个核心要素：技术知识(TK)、教学法知识(PK)、学科内容知识(CK)，紧接着由三者相互融合形成了整合技术的学科内容知识(TCK)、学科教学知识(PCK)、整合技术的教学法知识(TPK)，最后这三者复合成为整合技术的学科教学知识(TPACK).目前，TPACK框架已经在教学设计上得到了一定的应用，它不仅使得教师关注到传统教学设计当中的基本要素，更加使得教师对技术知识有了一定的关注，这是使得学生动手“做数学”成为可能的关键，下面是对某一教学设计，借助TPACK框架进行分析的表格.

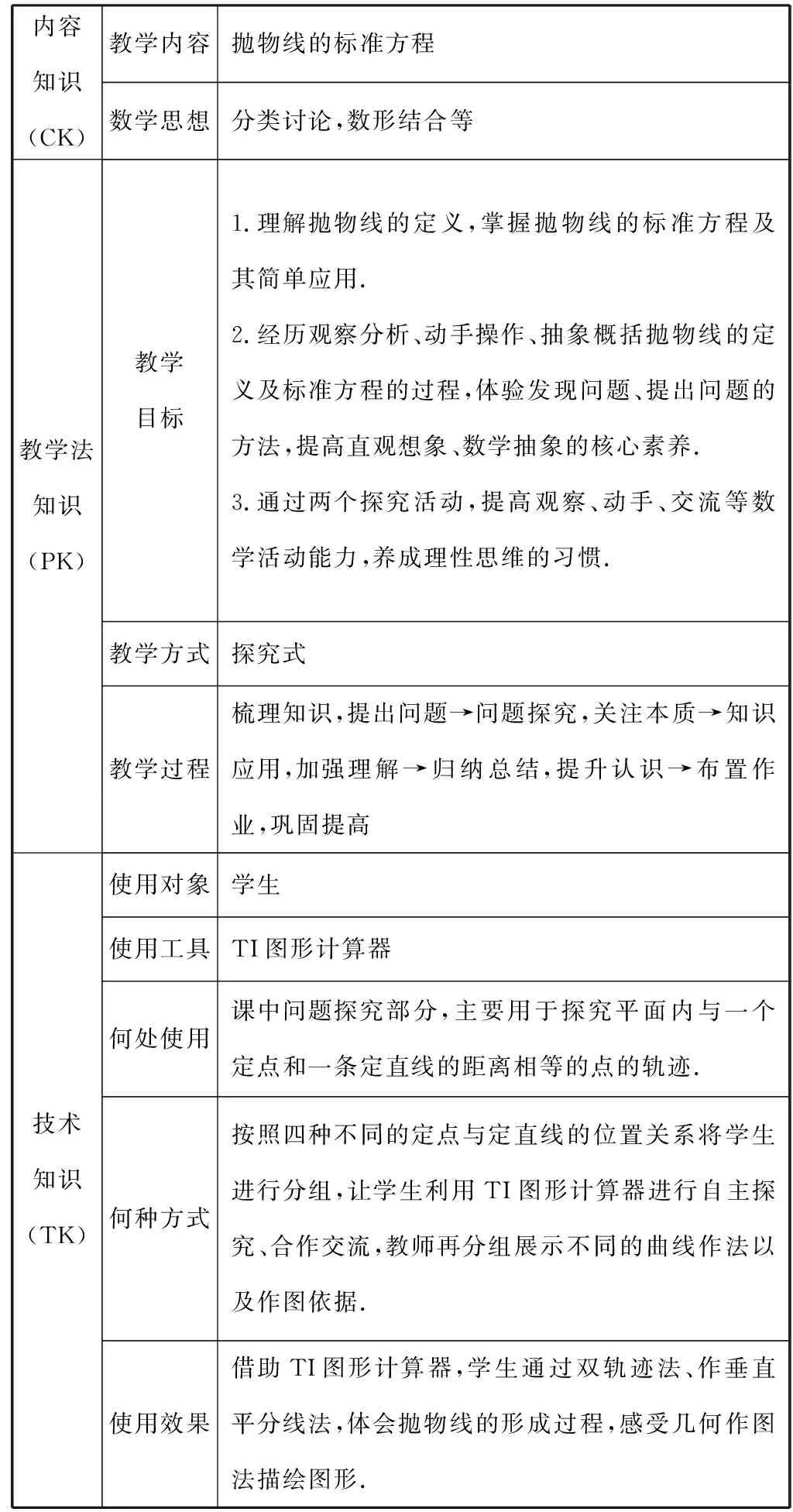
表1 基于TPACK框架的教学设计分析

2 TPACK框架下的深度学习

为使TPACK框架更好地作为实现深度学习的手段和途径，教师需将深度学习教学过程的五个环节与TPACK中的各要素有机融合.教师可以根据自身需要，先确定好TPACK框架中的相关内容，再将其融入深度学习的教学过程中.本文以“导数的几何意义”为研究重点.

3 围绕导数几何意义的TPACK视域下深度学习的教学案例

3.1 教学内容分析

“导数的几何意义”主要内容是：函数f(x)在x=x0处的导数的几何意义，本节课是承接前面的导数的概念.这里如何巧妙地推进信息技术与教育的融合是教师最需要解决的关键问题.

3.2 构成要素分析

关于导数部分，将TPACK框架与“导数的几何意义”结合，部分教师的实践跟不上认知.从教学的角度来看，教师应该设计更有效的任务，确保学生能够解决真实的问题，并评估解决问题的能力.在教学设计的过程中，教师应该利用更多的网络资源来探索学科前沿知识，设计跨学科的教学活动，从而更好地设计深度学习与TPACK框架相结合的教学过程.TPACK构成要素分析如图1.

图1 TPACK构成要素分析

3.3 教学过程与设计意图

3.3.1 布置学习任务

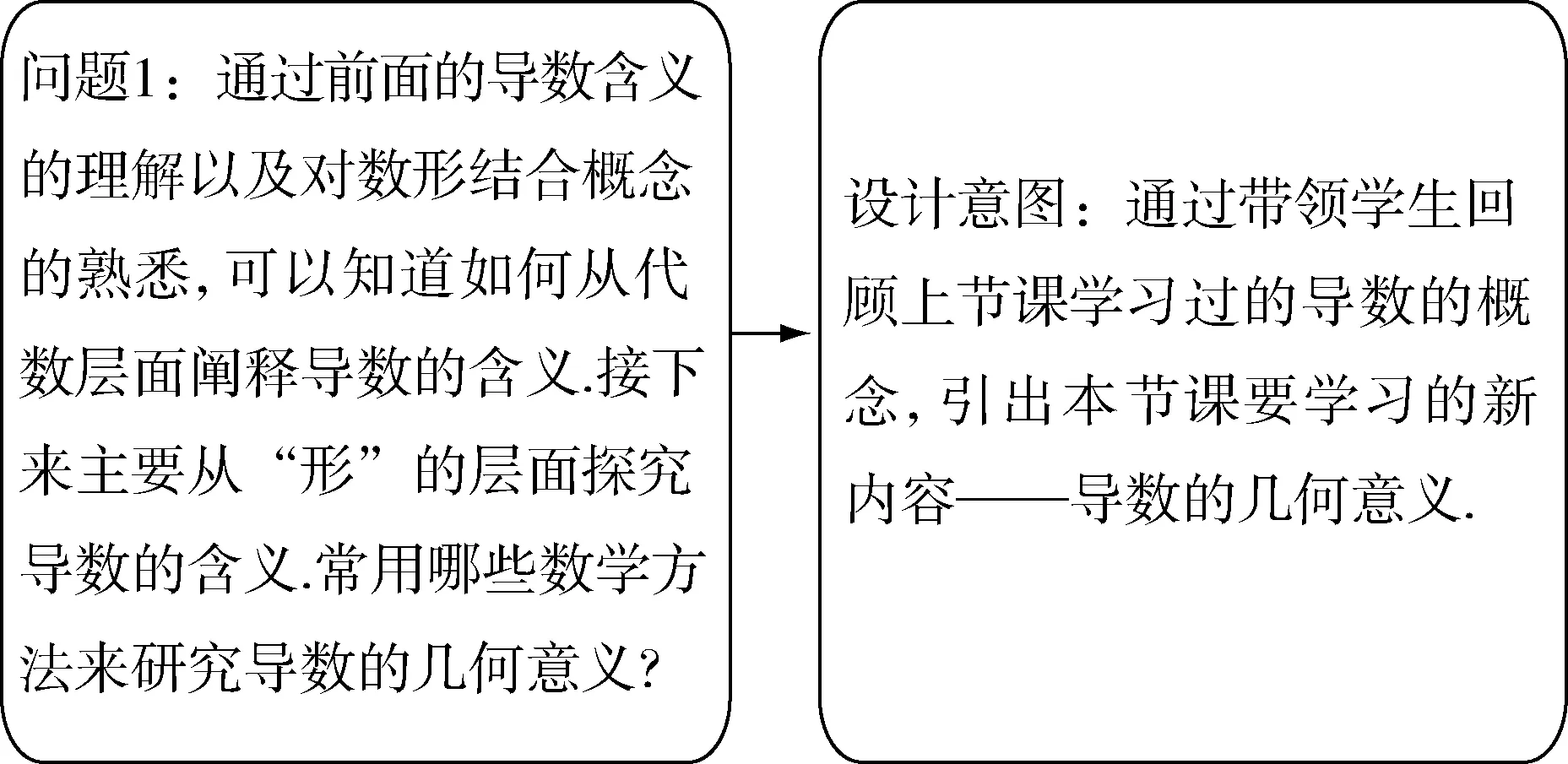
图2 问题1逻辑与求解

从某种意义来说，本节课的内容是导数的概念的延伸，教师需唤起学生对导数的几何意义的思考，使得学生更加全面地建构起关于导数的知识体系.

3.3.2 深入探究，获取数学本质

通过上面的充分准备，小组学习继续深入探究，以此来获取数学本质.

图3 问题2逻辑与求解

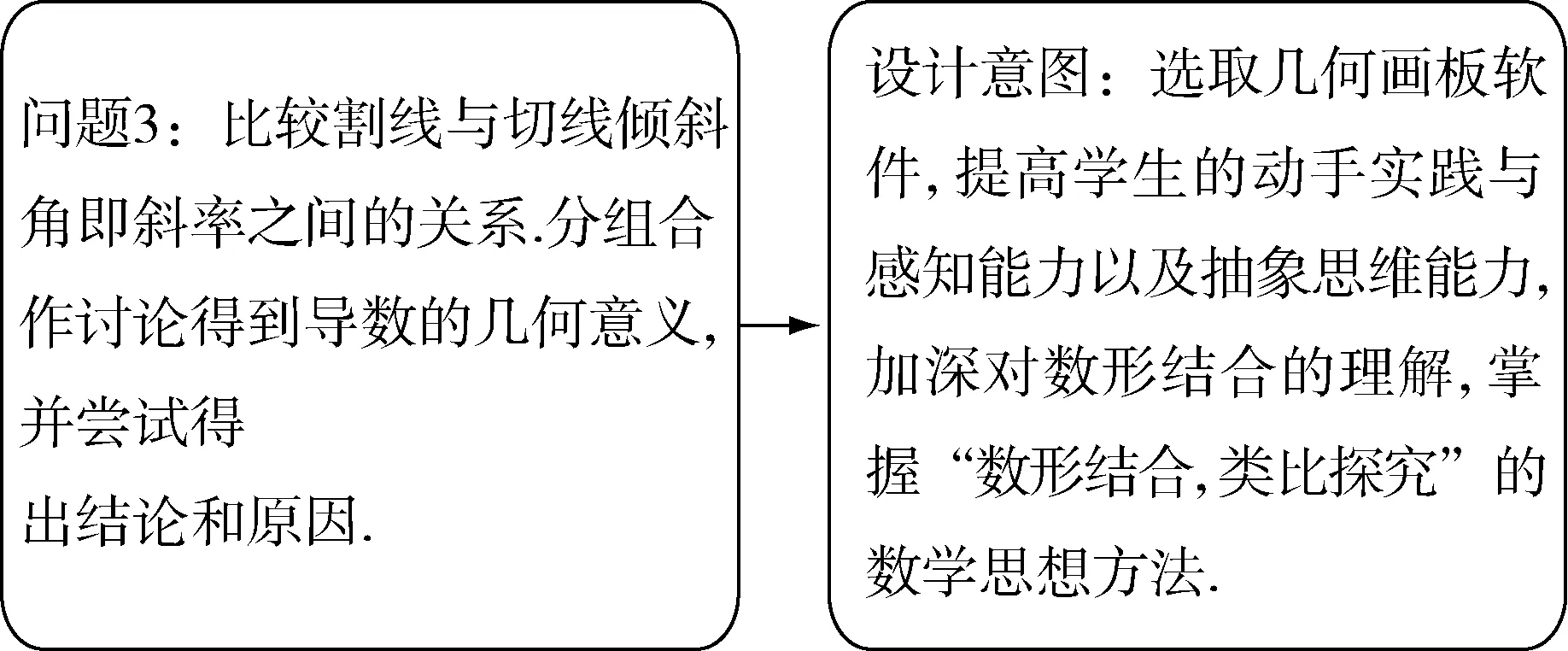
图4 问题3逻辑与求解

3.3.3 巩固知识之间的联系

在对导数有初始了解的基础上，教师将练习题目与基础知识相结合，强化学生对导数几何意义的理解.

完成练习：例题1(课本第68页例4)、例题2(课本第69页例5).

设计意图：教师带领同学们以练习习题为主，通过对习题的演练让同学们理解本节课的重点内容，并带领同学们利用导数的含义来完成对实际问题的求解.在与技术相结合的评价维度上，高中教师通过大量的作业来帮助学生掌握回答问题所需的技能，培养学生的数学思维和解决问题的能力，这有利于学生对导数数形结合方面的深层了解.

3.3.4 总结学习过程

我们应调查不同领域教师专业知识发展的环境，并确定有助于专业知识发展的积极因素，以加强单一领域教师能力的发展.教师TPACK能力的发展与不同的教育阶段相联系.教师获得一个新的知识基础和技能可能是一项挑战.随着时间和文化的变化，以及新的技术蕴含的教育应用潜力，教师必须相应地调整他们的知识、实践和技能.就教育而言，教育政策制定者、利益相关者、研究人员和教育工作者认为，从学校向数字时代的转变对学生参与当代社会至关重要.

4 意义与展望

TPACK框架下，学生能够自主挖掘相关知识的联系，使得点状知识相互联结生成网状知识，从而能够深刻理解和把握数学的本质，最终完成从“学会”到“会学”的过渡.