用整体法快解高中物理选修3-3四种常考模型

罗玲秀

摘要：某卫视的《男生女生向前冲》节目设置男女生双赛道，其中有直线冲关，跳台挑战，旋转圆台，绳子爬坡，大球摆动等环节，在我们物理老师看来就是一系列运动模型的结合，匀速直线运动，匀速与非匀速圆周运动，不同抛体运动等模型，这个游戏就是学生答题的反应，学生只有逐一掌握每个运动模型，才能在最后高考中拿下24.25两个大题。学习物理是有方法的，我们得引导学生分析题干，构建模型。本文引入物理选修3-3的四个常考模型，分别用整体法和隔离法解题，通过比对，让学生学会用整体法更快解题。

关键词：整体法;解题;物理选修3-3物理模型

一、往年考题汇总

从近几年高考题来看，如图1，对于热学内容的考查形式比较固定，一般第（1）问为选择题 ，且为“5项选3项”，主要考查分子动理论、内能、固体及液体的性质、气体实验定律、热力学定律等问题，2021年再次出现了考查涉及气体的图像;第（2）问为计算题，主要考查气体实验定律、理想气体状态方程的应用，且多以液体封闭或活塞封闭的气体为背景命题。

二、四种常考模型

（一）条件模型——一定质量理想气体

气体实验定律及理想气体状态方程均适用于一定质量理想气体，但在实际问题中，常遇到气体的变质量问题;解答气体的变质量问题时，可以通过巧妙地选择合适的研究对象，把“变质量”问题转化为“定质量”的问题，从而可以应用气体实验定律或理想气体状态方程求解，类似于把分散个体整体化，变质量常见以下四种类型：

①充气（打气）问题

在充气（打气）时，将充进容器内的气体和容器内的原有气体为研究对象时，这些气体的质量是不变的.这样，可将“变质量”的问题转化成“定质量”问题.

②抽气问题

在对容器抽气的过程中，对每一次抽气而言，气体质量发生变化，解决该类变质量问题的方法与充气（打气）问题类似：一定要把所有抽出的气体算在整个过程气体变化的计算中，就可以让“变质量”变为“定质量”可利用气体定律解决的问题.

③灌气（分装）问题

把某个大容器里的气体分别灌到不同的小容器中，这时候大容器中气体发生改变是变质量问题，但是我们所研究的气体本身并没有消失，解决这个问题很容易，只需要把大容器中的气体跟所以小容器中的气体看作一个整体来进行研究，就可以让“变质量”变为“定质量”可利用气体定律解决的问题.

④漏气问题

容器漏气过程中容器内气体不断释放到空气中这样容器内部剩余的质量时刻发生改变，属于变质量问题，气体实验定律研究的是一定质量的气体，容器内剩余气体加上释放在空中的气体当作研究对象，就可以让“变质量”变为“定质量”可利用气体定律解决的问题.

（二）过程模型——等温变化

通过历年高考命题一览表我们不难发现等温变化在计算题中考察最频繁，这个与我们的生活息息相关，完美地诠释物理来源于生活又应用与生活的真理。题干简单易懂学生比较容易理解。

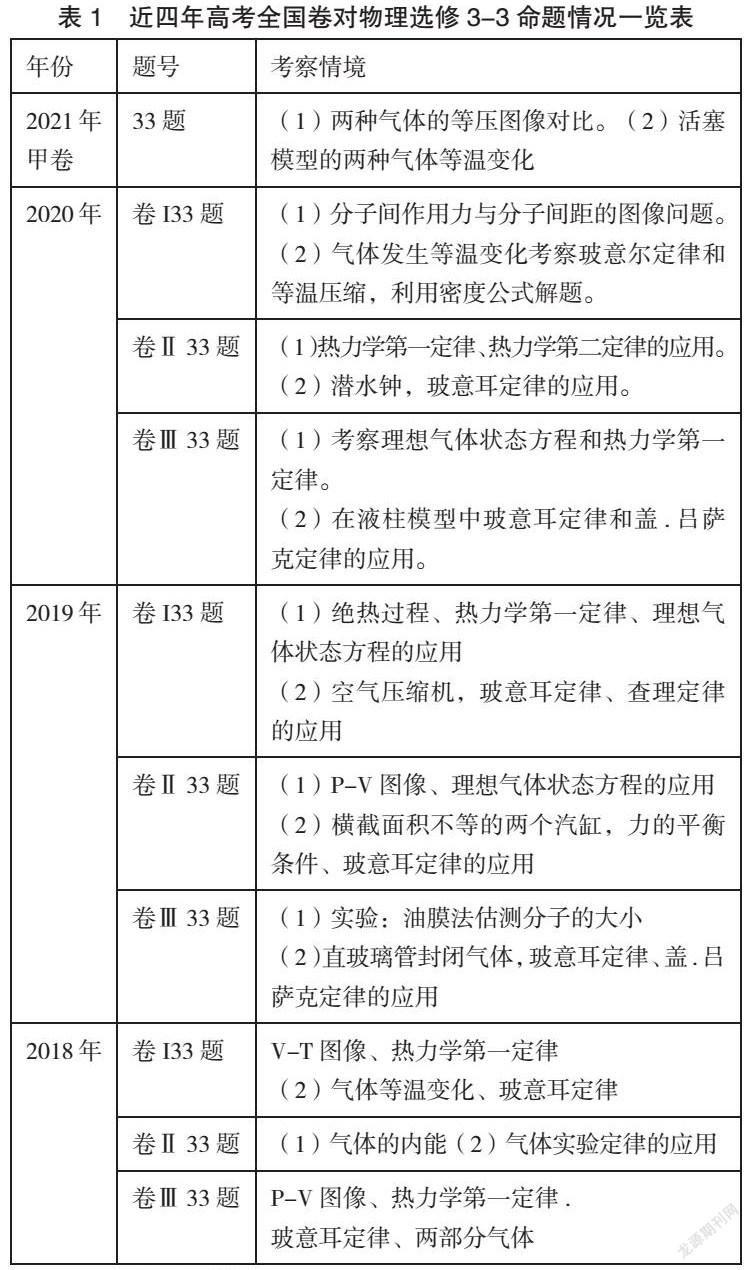
例题一、如图所示，两端开口的U型管粗细均匀，左右两管竖直，底部的直管水平，水银柱的长度如图中标注所示，水平管内两段空气柱a、b的长度分别为10cm、5cm.在左管内缓慢注入一定量的水银，稳定后右管的水银面比原来高h=10cm.根据大气压强为76cmHg，求向左管注入的水银柱长度。

分析：根据玻意耳定律分别利用隔离法与整体法求出注入水银后两部分气体的长度，再结合几何关系即可求解向左管注入的水银柱长度。

解答：用隔离法

初状态a、b两部分空气柱的压强：P1═76cmHg+14cmHg=90cmHg…①因右管水银面升高的高度10cm<12cm，故b空气柱仍在水平直管内。末状态a、b两部分空气柱的压强：P2=76cmHg+14cmHg+10cmHg=100cmHg…②

设末状态a、b两部分空气柱的长度分别为La2、Lb2：对a部分空气柱，根据波意耳定律：P1La1S=P2La2S…③对b部分空气柱，根据波意耳定律：P1Lb1S=P2Lb2S…④代入数据解得：La2=9cm      Lb2=4.5cm左管所注入的水银柱长度：L=2h+（La1+Lb1）-（La2+Lb2）…⑤代入数据解得：L=21.5cm…⑥答：向左管注入的水银柱长度为21.5cm.

解答：用整体法

本题中ab两部分中间虽然有一部分水银柱，但是水银柱的长度并没有变化，更没有影响ab空气柱的变化，最主要的是这两部分空气柱的初、末温度合初、末压强都相等，本题中应该将ab空气柱看作一个整体。整体初状态气体长度L1=15cm，设末状态整体长度为L2由玻意耳定律得P1L1S=P2L2S，代入解得L2=13.5cm所以向左管中注入水银柱的长度为：L=2h+（L1-L2）=21.5cm

（三）过程模型——等压变化

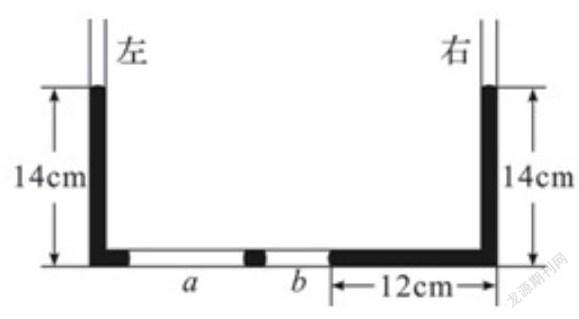
例题三.如图所示，透热的气缸内封有一定质量的理想气体，缸体质量M=200kg，活塞质量m=10kg，活塞面积S=100cm2。活塞与气缸壁无摩擦且不漏气，此时缸内气体的温度为27℃，活塞正位于气缸正中，整个装置都静止已知大气压恒为p0=1.0×105pa，重力加速度为求g=10m/s2：

（1）平衡时弹簧弹力F（2）缸内气体的压强p1;

（3）缸内气体的温度升高到多少时，活塞恰好会静止在气缸缸口AB處？

解答：（1）平衡时弹簧弹力与活塞接触，若是对活塞进行受力分析则先是缸内气体的压强p1不知，当求缸内气体的压强p1时还是的选择气缸为研究对象，算下来过程多，当我们放大视野拓展思路发现当以活塞气缸为整体研究时能更快解题。平衡时弹簧弹力F=（M+m）g=2100N（2）以气缸为对象（不包括活塞）列气缸受力平衡方程：p1S=Mg+p0S解之得：p1=3×105pa  （3）当活塞恰好静止在气缸缸口AB处时，缸内气体温度为T2，压强为p2此时仍有p2S=Mg+p0S，即缸内气体为等压变化。对这一过程研究缸内气体，由状态方程得：所以T2=2T1=500K故t2=（600-273）℃=327℃

（四）过程模型——等容变化

例题二、如图，在温度为T0大气压强为P0固定一个水平放的装置圆筒，它组成是前中后大小不同连接而成，前中后部分的圆底面积之比是2：12：1，封住容器的两活塞用一根长为4L的轻线相连并且无法伸长，把空气密封在两活塞之间。这时两A、B活塞的位置如下图所示.（活塞与圆筒壁之间的摩擦可忽略）

（1）缓慢加热被密封在容器中的气体，当活塞B向左移动距离刚好为L时，求封闭气体的温度;

（2）当气体温度缓慢上升到2T0时，求两活塞之间轻线的拉力。

分析：（1）对活塞A、B分别根据平衡条件列式，绳子拉力一样两个平衡等式联力即可求出封闭气体压强，不过讲题时引导学生活塞A、B看作一个整体，只用一个等式即可求解。将活塞向左移动，气缸内的气体发生等压变化，根据盖-吕萨克定律即可求解活塞B向左移动距离刚好为L时，封闭气体的温度;（2）气缸气体发生等容变化，由查理定律求出温度为T2时的气体压强，再对活塞A根据受力平衡求出两活塞之间轻线的拉力;

解答：（1）用p 1表示被封闭气体被加热前的压强，对活塞AB用整体法则根据平衡条件有：2p0S-2p1S+p1S-p0S=0解得：p1=p0表示被封闭气体被加热前的压强跟大气压强一样，轻线处在拉直的松弛状态，这时气体的体积为：V1=2Sl+Sl+Sl=4Sl缓慢对气体加热过程中，被密封气体温度缓慢升高，两活塞一起向左缓慢移动，气体体积逐渐增大，但是压强保持p 1不变，若持续加热，此过程会一直持续到活塞向左移动的距离等于L为止，这时气体的体积为：V2=4Sl+Sl=5Sl根据盖-吕萨克定律得：V2T2=V1T0解得：T2=1.25T 0

（2）由于T=2T0>T2时，活塞已无法移动，被密封气体的体积保持V2不变，由查理定律得：

pT=p0T2解得：p=85p0对活塞A受力分析p02S+F=p2S解得F=1.2p0S

物理是一门来源于生活，又解释生活的学科，学生在学习物理过程中没有将题目抽象化构建不同物理模型，那么学生上课时就容易走神，更不用说完成学习要求考上好大学，对生活中所遇到的例子更不能构建出相应的模型去解决问题，学习物理是化整为零，逐个击破每个物理模型，才能在综合性学习中取胜！

參考文献：

[1] 林明华.高中物理教学中科学思维教育的落实[J].物理教学探讨，2018（10）.

[2]彭前程.《普通高中物理课程标准（2017年版）》的变化[J].课程.教材.教法，2018（09）.