联合样本输出与特征空间的半监督概念漂移检测法及其应用

孙子健 汤 健 乔俊飞

城市固废(Municipal solid waste,MSW)的全球年增长率随城镇人口增加和居民消费水平提高而不断增加[1],我国部分城市甚至陷入 “垃圾围城”困境[2].该现象直接危害环境卫生和生态平衡,因此MSW 处理成为亟待解决的全球性问题.具有无害化、减量化和资源化等特点的MSW 焚烧(Municipal solid waste incineration,MSWI)是世界范围内广泛采用的措施[3],但该过程的排放尾气中含有氮氧化物、二噁英等难以检测的有害污染物.目前,MSWI 企业主要通过控制焚烧运行参数实现污染物排放浓度的控制.显然,实现MSWI 过程污染物排放最小化的关键之一是实时、精准地测量这些难测参数的排放浓度[4].对此,软测量模型因具有经济性和快速性等优点而成为当前最为常见的实时测量策略[5].但是,由于工业过程多具有复杂性、随机性和时变性等特征,这使得基于历史数据构建的软测量模型因不能覆盖新样本所表征的数据分布而导致泛化性能恶化,导致这一现象的本质原因是概念漂移[6].

概念漂移可表述为数据分布随时间发生变化,从软测量模型的视角可理解为样本输出空间与特征空间的映射关系发生了改变[7].该现象是由难以预知的工业生产环境改变、物料成分波动和设备磨损与维护等因素引起,并难以避免地导致模型测量精度显著降低[6].例如,MSWI 过程中的炉膛温度变化可使烟气污染物生成关系改变,MSW 含水率的差异会导致炉内燃烧状态的变化[3],这些现象均会引起概念漂移,进而使得基于历史数据构建的污染物浓度测量模型的精度下降[8].因此,如何采用漂移检测方法有效识别能够表征新概念的漂移样本并将其用于软测量模型的更新,是提高模型泛化性能需要解决的首要问题[9].

有监督型漂移检测的代表性算法是漂移检测法(Drift detection method,DDM)[10−11],其根据新样本测量性能定义警告与漂移等级.当测量误差超过警告等级时,存储新样本;当超过漂移等级时,采用存储的新样本及历史样本构建新模型以代替旧模型.类似地,文献[12]计算模型在总体样本和最近样本中获得可接受测量误差的概率,采用Hoeffding 不等式判断概率差异后确认是否发生漂移;文献[13]通过比较模型更新前后输出权重值的变化程度表征漂移;文献[14−15]分别采用指数加权移动平均和Page-Hinkley 检测法确认模型测量精度的变化,以判断是否发生了概念漂移.由上可知,难测参数的测量误差变化能够表征概念漂移对测量模型的直接影响,该类方法具有计算过程简便高效的优点;但面向实际工业过程,上述算法忽视了难测参数真值无法全部获取的实际现状.例如,在MSWI过程中,氮氧化物的排放浓度采用人工采样分析方法时其真值获取周期过长,采用烟气传感器检测时其易受恶劣工况影响而导致测量失真[16];二噁英的排放浓度因其采样与化验分析的复杂性导致其真值标注周期长且成本高昂[3].因此,上述有监督型漂移检测方法难以在实际工业过程中直接使用.

无监督型漂移检测的代表性算法有:文献[17−19]基于多元统计策略分别采用近似线性依靠(Approximate linear dependence,ALD)条件、主成分分析(Principal component analysis,PCA)和角度优化全局降维算法(Angle optimized global embedding,AOGE)分析样本特征空间的分布变化;文献[20−21]基于距离度量策略采用马氏距离和领域熵度量特征空间的概念变化;文献[22−23]基于假设检验策略提出基于重采样和累计区域密度的检测方法.该类算法的特点是在漂移检测阶段不依赖难测参数真值,但在模型更新阶段仍需采用标注真值的样本,因此难以在短期内使得模型具有对漂移的适应能力[24].

此外,复杂工业过程中概念漂移的影响会同时体现为模型测量误差和样本特征空间的综合变化.因此,仅基于样本特征空间的分布差异难以有效表征概念漂移现象[10].针对上述问题,面向分类任务,文献[25]提出半监督漂移学习框架,通过监视分类器置信度变化初步筛选漂移样本,再根据置信度得分估计漂移样本的伪标签,最后进行模型更新.类似地,文献[26]提出基于密度估计的半监督漂移检测,在少量有标注样本前提下采用增量估计器标注其余样本的标签而实现漂移检测.但目前为止,面向复杂工业过程回归建模领域的半监督概念漂移检测方法鲜有报道.由于分类任务常具有明确且有限的类别标签用于划分样本概念,其算法设计方式不适用于连续型变量,因此上述方法难以直接用于回归建模领域[27].

综上,本文充分考虑MSWI 过程中的概念漂移现象和难测参数真值无法及时获取的问题,提出联合样本输出与特征空间的半监督漂移检测方法.首先,采用高斯过程回归(Gaussian process regression,GPR)依据历史样本构建离线测量模型;然后,采用基于PCA 的无监督机制检测特征空间漂移的样本并将其记录在待标注缓存窗口;接着,在样本输出空间中采用基于时间差分(Temporal-difference,TD)学习的半监督机制对上述缓存窗口内的样本进行伪真值标注,并采用Page-Hinkley 检测法确认能够表征概念漂移的新样本;最后,采用新样本与历史样本更新软测量模型.

1 城市固废焚烧(MSWI)过程概念漂移问题描述

1.1 城市固废焚烧过程描述

MSWI 过程主要由固废储运、固废焚烧、蒸汽发电、烟气处理和烟气排放等系统组成,其工艺流程如图1 所示.

结合图1,针对固废焚烧阶段可描述如下[3].

MSW 由抓斗投放至进料器并送入炉排式焚烧炉.经干燥炉排预热后,MSW 通过一次风机输送的助燃空气在燃烧炉排中着火燃烧,在燃烬炉排内燃烧完毕,产生的烟气经二次风机产生的高度湍流分解后进入烟气管道.该阶段中,难测参数氮氧化物的生成原因主要包括[28]:1) MSW 本身含有的有机和无机含氮化合物在焚烧过程中与氧气发生化学反应;2) 一次风和二次风中的氮气高温氧化;3) 助燃燃料(汽油等)高温裂解.因此,炉膛温度、炉膛含氧量、烟气停留时间与湍流程度等因素改变均会使氮氧化物生成关系变化并产生概念漂移.

传统MSWI 过程常通过人工化验和烟气自动监控系统(Continuous emission monitoring system,CEMS)测定氮氧化物排放浓度.其中,人工化验主要包括在线采样和离线化验,该方式测定周期较长且远滞后于实际过程,因此无法向测量模型及时提供真值[3];CEMS 常通过完全抽取或稀释抽取进行测量,前者在正压环境或抽气量过大时易发生抽气口堵塞,后者测量响应时间过长且对干燥压缩空气纯度要求高,此外CEMS 需要有资质的技术人员定期维护[16].上述方式均导致难测参数的真值获取困难.因此,需通过标注难测参数的伪真值,以在无法获取全部真值的情况下分析过程中存在的概念漂移现象.

1.2 概念漂移问题描述

工业过程中通常根据概念漂移的产生原因将其分为过程漂移和传感器漂移[29].其中,过程漂移包括过程内部结构变化(机械元件磨损等)和过程外部条件变化(气候与工艺要求等);传感器漂移常由传感器等硬件设施的测量精度改变导致,不反映运行过程的真实参数变化.本文主要研究MSWI 过程中常见的概念漂移形式,即由过程外部条件变化引起的过程漂移.

结合文献[30]中定义,此处对工业过程中概念漂移问题描述如下:

根据描述,常见概念漂移处理方式如图2 所示.

图2 中,虚线框表示该部分内容并非始终可用(样本真值);分布信息提取指通过测量误差、多元统计或假设检验等方式收集可表征样本分布特性的关键信息;分布差异检测是针对已提取信息通过预设规则进行相似度量;依据检测结果,最终由具体算法判断新样本是否用于更新或舍弃[11].

图2 常见概念漂移处理方式Fig.2 The common way to deal with concept drift

2 概念漂移检测算法策略

依据上文分析,本文提出联合样本输出与特征空间的半监督概念漂移检测算法,其策略如图3所示.

图3 中各模块功能描述如下:

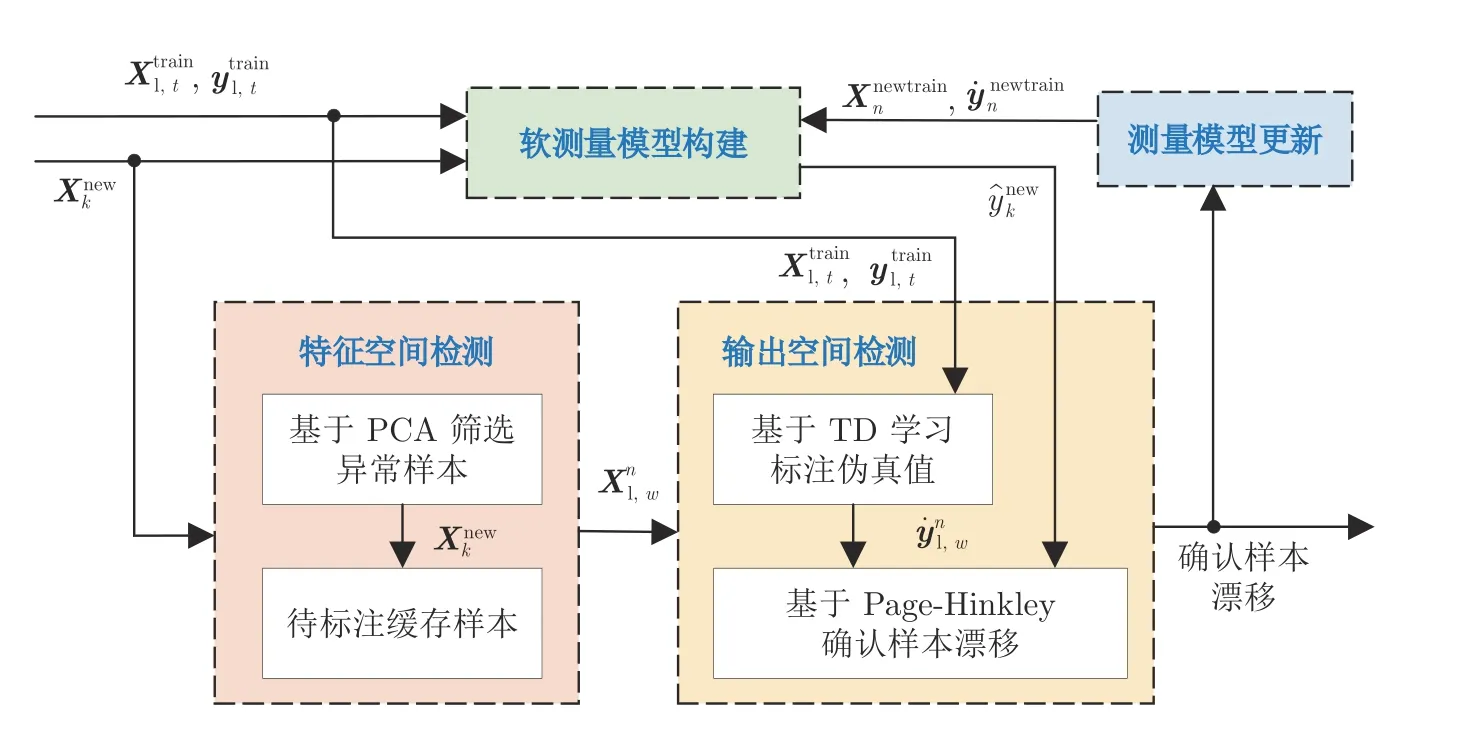
图3 本文算法策略Fig.3 The strategy of the proposed algorithm

1) 软测量模型构建.采用历史样本构建基础软测量模型,并依据新样本的特征空间输出测量值.

2) 特征空间检测.采用PCA 对新样本的特征空间进行漂移检测,当检测值超过PCA 控制限时认为样本具有漂移可能性,此时将该样本存入待标注缓存窗口,当窗口内样本数量达到预设窗口容量时将这些样本送入输出空间检测模块.

3) 输出空间检测.基于TD 学习对待标注缓存窗口内样本的伪真值进行标注,再采用Page-Hinkley检测法分析样本的伪真值与模型测量值差异,以确认样本是否漂移.

4) 测量模型更新.确认当前缓存窗口内样本发生概念漂移后,将其结合历史样本共同构造为新训练集重新训练软测量模型,同时重置待标注缓存窗口.

3 概念漂移检测算法实现

3.1 软测量模型构建模块

本文采用GPR 构建基础软测量模型.GPR 通过贝叶斯推理确定样本复杂性水平并建立特征空间与输出空间的映射关系,现已广泛应用于多种工业领域[32].

3.2 特征空间检测模块

3.3 输出空间检测模块

3.3.1 基于时间差分(TD)学习的伪真值标注

伪真值标注是实现半监督漂移检测的前提.现有研究中,文献[36−37]证明TD 学习对特征空间漂移的样本具有良好的测量性能.TD 学习通过分析样本输出与特征空间的一阶差分量变化实现新样本测量[38],其思路描述如下.

具体标注策略为:根据式(7)、式(8),计算历史样本输出与特征空间的一阶差分量集合分别为∆ytrain和 ∆Xtrain,并请求现场人员标注窗口内第一个样本的真值.原因是:1) 实际工业过程存在成本高昂、检测延迟和维护困难等问题,导致难以对全部样本进行真值标注;2) 新样本发生概念漂移时,其输入输出关系相较历史样本有较大改变,此时仅依据历史样本难以推断漂移样本的伪真值.综上,仅标注窗口内第一个样本的真值,可在缩减标注成本的同时提高后续伪真值标注工作的准确性.据此,构建新一阶差分量集合为:

3.3.2 基于Page-Hinkley 检测法的漂移样本确认

合理分析样本伪真值和测量值间的差异,是确认样本最终概念漂移情况的关键.现有研究表明,基于累积和思想推导的Page-Hinkley 检测法具有对分布漂移敏感、计算简便等特点,因此可有效用于输出空间漂移检测[24].该方法中,给定一系列观测值 [l1,l2,···,lm],计算备择假设(观测值中存在漂移点θ,即 1<θ m)的似然比统计量为[39]:服从数学期望为δ的正态分布.

式(20)以对数表示为:

据此,备择假设(有漂移) 对原假设(无漂移)的对数似然比统计量为:

通过设置阈值与Zm进行比较,即可判断当前系列观测值内是否存在概念漂移.

当待标注缓存窗口内样本均完成伪真值标注后,本文采用Page-Hinkley 检测法对这些样本的输出空间进行概念漂移检测.以T时刻的观测值Obs(T)为例,检测流程如下[24].

首先,计算关于Obs(T)的累计变量φT:

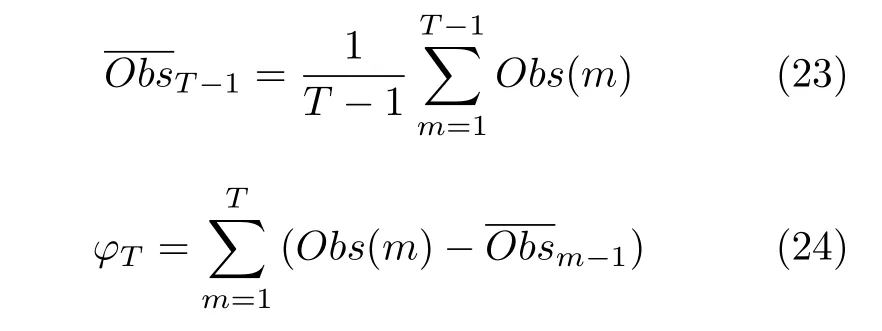
其中,ObsT −1表示此前T−1 时刻所有历史观测值的均值;累计变量φT表示当前观测值Obs(T)与历史观测值均值之差.

然后,通过计算变化指标PHT判断当前观测值Obs(T)是否异常:

式中,ϕT表示当前所有时刻中记录的最小累计变量值;PHT表示当前T时刻累计变量φT与最小累计变量值之差.当满足条件PHT >λ时,认为观测值Obs(T)异常,其中λ是经验阈值.

在此基础上,本文将观测值Obs(T)选取为窗口第n次填满时窗口内样本的累积平均测量误差,即:

此时,累计变量φT表示当前累计平均测量误差与历史累计平均测量误差均值之差;ϕT表示当前记录的最小φT值.

此外,根据式(26),缓存窗口第一次被填满即n=1 时,ϕT=φT,此时样本输出空间中缺乏漂移判断依据,因此本文将ϕT表示为:

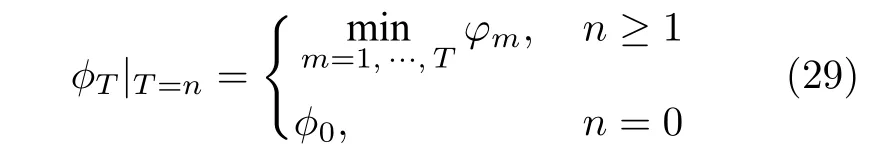
式中,ϕ0为基准累计平均测量误差,将依据验证样本平均测量误差获得.同时,本文设置λ=0,即当φT >ϕT,代表当次窗口内累计平均测量误差相较历史样本明显升高时,认为窗口内样本可表征概念漂移,并将其用于构建新训练集.

3.4 测量模型更新模块

当缓存窗口内样本被确认漂移后,本文根据历史样本和当前窗口内样本共同构建新训练集对测量模型进行更新.以缓存窗口被第n次填满时窗口内样本为例,构造新训练集如下:

4 仿真分析

4.1 数据集

本文采用合成数据集验证所提方法的有效性,并通过真实MSWI 过程数据集验证其实际应用效果.

1) 合成数据集

合成数据集采用文献[40]所提方法构建.正常样本生成依据为:

式中,x1、x2、x3、x4和x5均服从[0,1]区间内均匀分布,σ(0,1) 是服从正态分布的随机数.

漂移样本生成依据为:

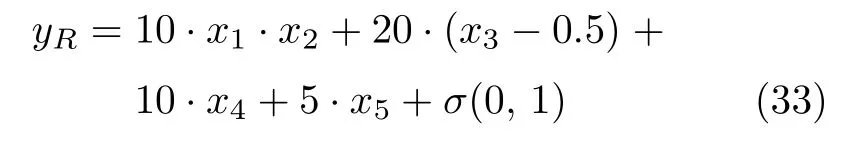
式中,各特征取值范围满足:

合成数据集共有样本1 500个,其中前1 000个为正常样本,后500个为漂移样本.在正常样本中,又划分前500个为建模样本,后500个为验证样本.验证样本设置目的是获得式(29)中基准累计平均测量误差ϕ0值.

2) MSWI 过程数据集

MSWI 过程数据来自北京市某MSWI 发电厂,数据中包含的缺失值和异常值均根据现场经验以人工方式去除.实验中选择氮氧化物的排放浓度作为测量目标,考虑其生成和吸收过程,选取炉膛温度、一次风量、二次风量、炉膛剩余氧量、尿素喷入量等相关性较强的18个变量作为样本特征.过程数据集中具有样本1 500个,其中前1 000个为正常样本,后500个为漂移样本.在正常样本中,又划分前500个为建模样本,后500个为验证样本.其中,正常样本在炉膛温度为900 ℃～950 ℃时的对应工况中采集;漂移样本在炉膛温度为950 ℃～1000 ℃时的对应工况中采集.

上述数据集的详细参数及各特征在概念漂移环境中的变化情况,如表1 和图4 所示.

表1 各数据集参数介绍Table 1 Detailed introduction of each data set

由图4 可知,两数据集中建模样本与漂移样本间的特征空间分布情况具有明显差异,间接反映了数据集中存在的概念漂移现象.

图4 各特征在概念漂移环境中的变化情况Fig.4 Changes of each feature in the concept drift environment

4.2 仿真结果

实验中各参数设置如表2 所示.其中,ConfSPE和ConfT2分别为PCA 统计量控制限SPE 和T2的置信度;ϕ0为验证样本平均测量误差.上述参数通过实验确定.

表2 仿真参数设置Table 2 Simulation parameter setting

原始测量模型在各数据集中的测量结果如图5所示.由图5 可知,原始测量模型在两个数据集的漂移发生时刻(第500个样本)均产生较大的测量误差,并对此后的漂移样本均无法有效拟合.

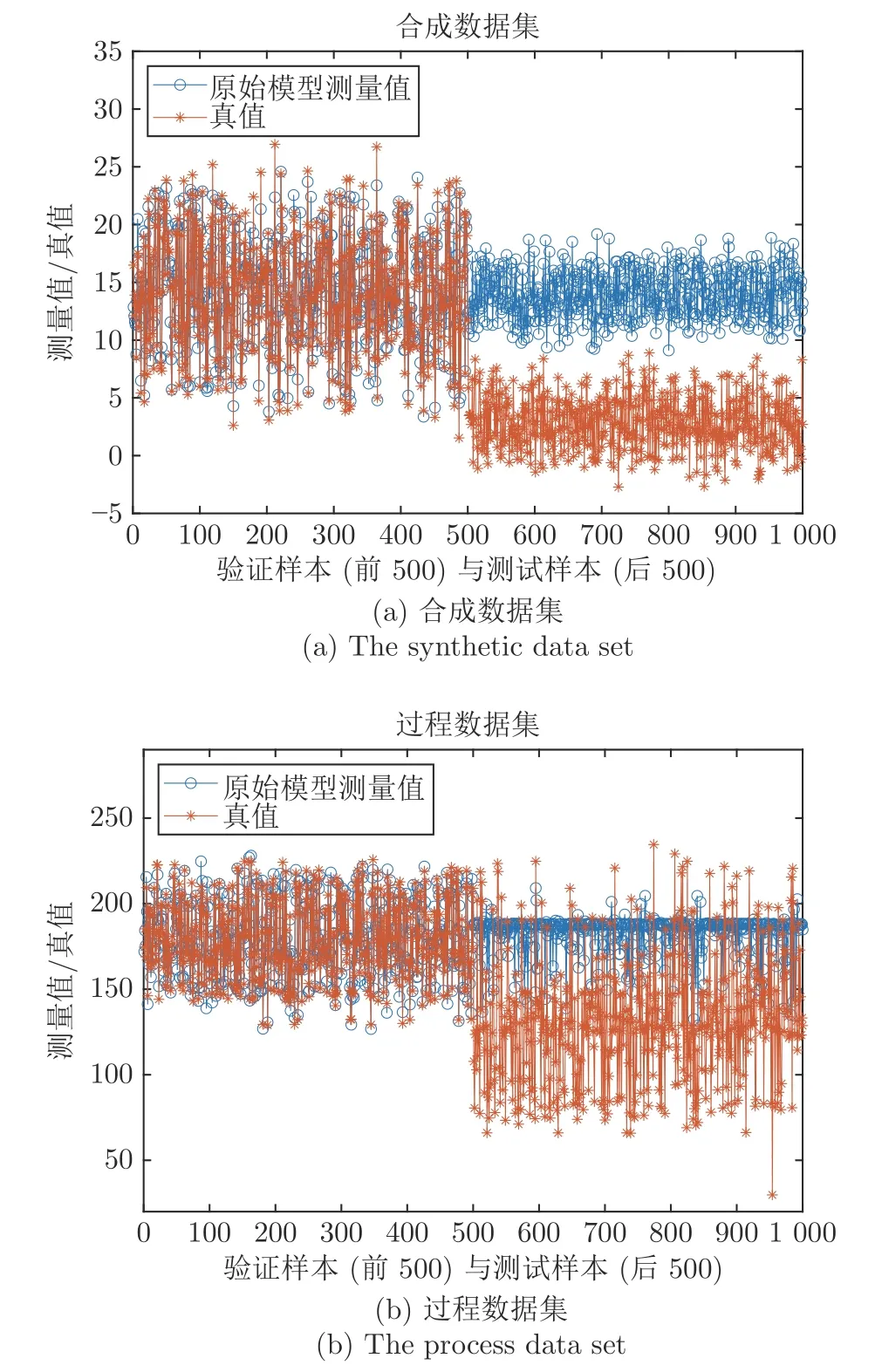
图5 原始模型测量结果Fig.5 Measurement results of the original model

1) 特征空间漂移检测

针对数据集中存在的概念漂移现象,采用PCA对验证样本和漂移样本特征空间的漂移检测结果如图6 所示.图中实线代表PCA 统计量,虚线代表统计量控制限.

图6 显示了验证样本和漂移样本特征空间的PCA 统计量与PCA 统计量控制限的大小关系.其中,在合成数据集中共测得特征空间漂移样本400个;在过程数据集中共测得特征空间漂移样本450个.从图6 可看出,过程数据集中样本特征空间分布对工况变化较为敏感,因此采用PCA 可有效测出漂移时刻对应样本.

图6 针对特征空间的漂移检测结果Fig.6 Drift detection results in the feature space

2) 基于TD 学习的伪真值标注

针对特征空间漂移的样本,基于TD 学习对其伪真值标注结果与实际真值的比较如图7 所示.其中,在合成数据集中共标注伪真值350个,伪真值与真值间平均误差为3.2760 (实际真值标准差为2.2606);在过程数据集中共标注伪真值441个,伪真值与真值间平均误差为35.9429 (实际真值标准差为36.3831),两个数据集中伪真值平均标注误差与实际真值自身离散程度相似.此外,从图7 可看出,伪真值变化趋势与样本真值相近,因此在样本真值难以完全获取时可采用伪真值对样本输出空间漂移情况近似分析.

图7 针对特征空间漂移样本的伪真值标注结果Fig.7 Pseudo-true value labeling results for samples with concept drift in the feature space

3) 输出空间检测结果

对特征空间漂移的样本完成伪真值标注后,采用Page-Hinkley 检测法对样本输出空间的漂移检测结果如图8 所示.

图8 为每次待标注缓存窗口被填满且其中样本均被标注伪真值后,窗口内样本累计平均测量误差的变化情况.其中,在合成数据集中待标注缓存窗口填满50 次;在过程数据集中待标注缓存窗口填满9 次.从图8 可看出,窗口内样本累计平均测量误差在漂移发生时刻明显升高,随模型不断更新而趋于平稳,表明所提算法可有效检测样本输出空间中存在的概念变化.

图8 针对输出空间的漂移检测结果Fig.8 Drift detection results in the output space

4) 测量模型更新

依据上述检测结果,模型采用由概念漂移样本和历史样本组成的新训练集更新后,在各数据集中的测量性能变化如图9 所示.

由图9 可知,测量模型采用所提漂移检测算法后,其测量误差相较原始模型明显下降,详细更新信息及模型均方根测量误差(Root mean squared error,RMSE)变化情况如表3 所示.

图9 采用所提漂移检测算法后模型测量误差变化Fig.9 Changes of model measurement error after adopting the proposed drift detection algorithm

由表3 可知:1) 合成数据集中,算法在500个漂移样本环境下,共标注样本伪真值350个,更新后使模型RMSE 降低66.2%,相较原始模型真值需求量降低99.2%;2) 过程数据集中,算法在500个漂移样本环境下,共标注样本伪真值441个,更新后使模型RMSE 降低45.5%,相较原始模型真值需求量降低98.2%.上述结果表明:所提算法可在大部分漂移样本真值未标注情况下,显著提升模型面对概念漂移样本的测量性能,可有效提高MSWI 过程氮氧化物浓度软测量模型在漂移环境中的测量精度.

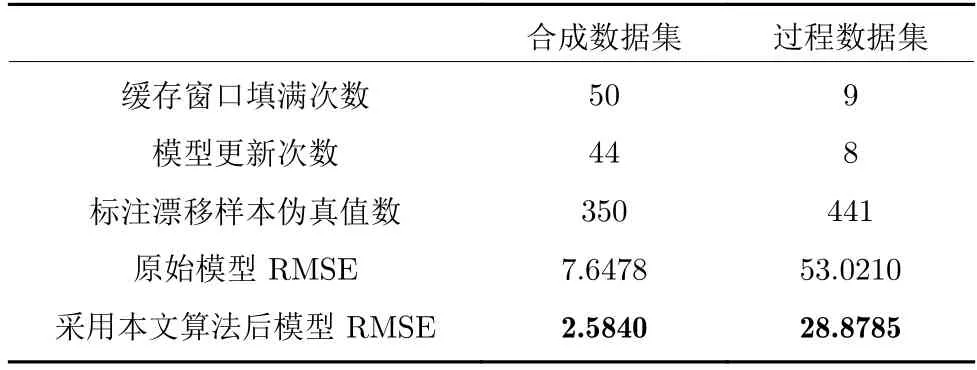
表3 所提算法检测信息Table 3 Detection information of the proposed algorithm

4.3 方法比较

1) 漂移检测性能比较

为验证所提漂移检测算法具有优于已有方法的性能,此处与仅基于特征空间的无监督型算法和仅基于输出空间的有监督型算法进行比较,前者基于PCA 检测样本特征空间漂移状况[19],后者采用模型测量误差检测样本输出空间漂移状况[41].比较结果如表4 和图10 所示.

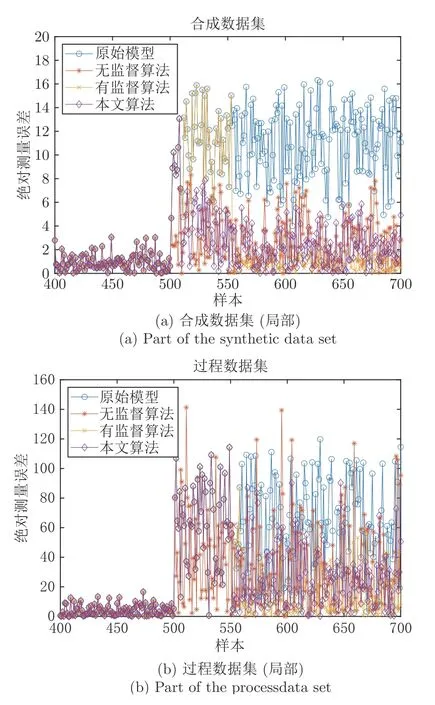
图10 采用不同算法时模型测量误差变化Fig.10 Changes in model measurement errors when using different algorithms

表4 不同算法检测性能比较Table 4 Comparison of detection performance of different algorithms

由上述结果分析可知:1) 相较无监督型算法,本文算法在两个数据集中均使模型更新后具有更低的测量RMSE 值,更新过程中真值需求量缩减50.5%(合成)、98.0% (过程);2) 相较有监督型算法,本文算法具有更低的更新次数,且在真值需求量分别缩减55.6%和98.0%的情况下,仍使模型更新后具有与其接近的测量RMSE 值.综上表明:所提算法可有效提升无监督型算法的更新效率,并在仅少量真值标注情况下保持与有监督型算法相近的更新性能.

2) 建模策略比较

为验证GPR 模型的高效测量性能,此处与两种常用机器学习模型:支持向量回归(Support vec-tor regression,SVR)和回归树(Regression tree,RT)进行比较.除模型外其余参数均与上文实验中保持一致,比较结果如表5 所示.

由表5 分析可知,上述模型均取最优测量结果时,GPR 表现仍优于其他模型.在合成数据集中,GPR 具有最优的训练RMSE、R2和测量RMSE(分别为0.1899、0.96 和2.5840);在过程数据集中,GPR 在训练阶段的拟合效果与SVR 相近(分别为0.1348 和0.98),但在测量阶段具有最优泛化性能(28.8785).

表5 不同模型测量性能比较Table 5 Comparison of measurement performance of different models

3) 近邻规则比较

为验证基于TD 学习的伪真值标注过程中欧氏距离作为近邻规则的有效性,此处与两种常用的相似性度量方式:曼哈顿距离与切比雪夫距离进行比较.比较过程中参数设置与实验部分保持一致,其结果如表6 所示.

由表6 分析可知,相较其他度量方式,欧氏距离能够体现特征空间数值上的绝对差异,而概念漂移样本相较历史样本常具有差异较大的特征值.因此,模型采用欧氏距离作为近邻规则时可较好捕获样本的相似性,并在各数据集中均具有最优测量性能(分别为2.5840 和28.8785).

表6 不同距离函数对模型更新性能影响Table 6 The influence of different distance functions on model updating performance

4.4 参数分析

仿真过程中固定参数(软测量模型核函数类型、核函数宽度、特征长度及基准累计平均测量误差ϕ0)根据模型最小训练误差与最小验证样本测试误差选取,可变参数(待标注缓存窗口容量w、PCA 控制限置信度ConfSPE、ConfT2及TD 学习最近邻数量ε)由实际仿真分析后选取.以过程数据集为例,不同可变参数对算法性能影响的分析结果如表7 所示.

由表7 可知:

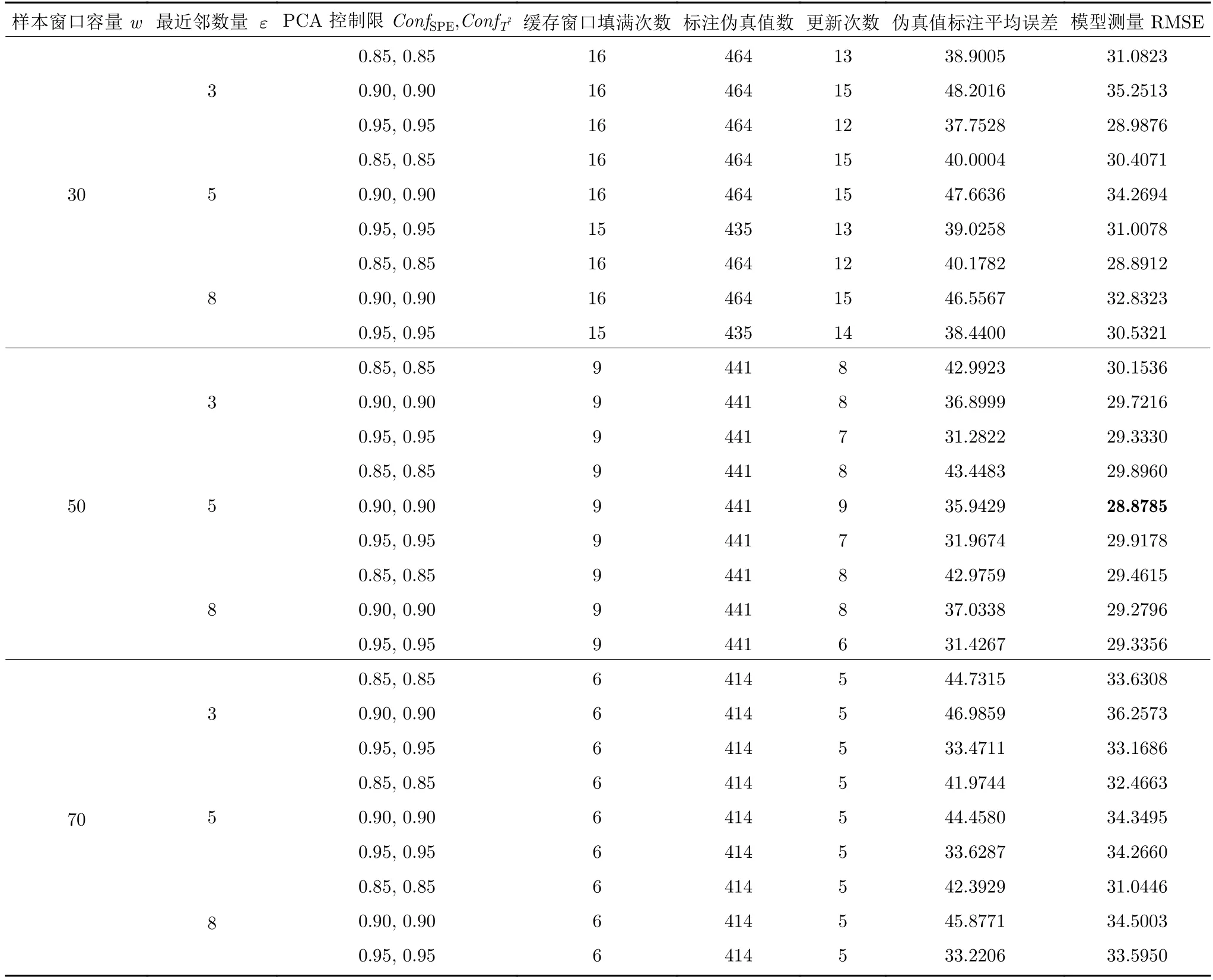
表7 不同可变参数对应算法性能变化Table 7 Algorithm performance changes corresponding to different variable parameters

1) 待标注缓存窗口容量w变化改变伪真值标注次数与模型更新次数,进而对更新后模型RMSE产生影响.当w偏小时缓存窗口易被填满,更多样本被检测为特征空间异常并被确认漂移,因此伪真值标注量与模型更新次数增加,但由于单次更新模型的漂移样本数过少导致模型无法在每次更新时充分学习漂移特征,易使更新后模型RMSE 偏大.当w偏大时缓存窗口难以填满,伪真值标注量与模型更新次数随之降低,但其较长的样本检索时间导致模型无法及时适应概念漂移,同样易使更新后模型RMSE 偏大.

2) TD 学习中最近邻数量ε变化改变伪真值标注精度,进而对更新后模型RMSE 产生影响.当ε偏小时被用于标注伪真值的历史样本数减少,因此算法无法获取充足的历史差分量变化信息,导致难以准确输出伪真值并易使更新后模型RMSE 偏大.当ε偏大时被用于标注伪真值的历史样本数增多,此时算法易受相似度较低的历史差分量变化信息干扰,同样导致更新后模型RMSE 偏大.

3) 特征空间漂移检测过程中PCA 控制限(ConfSPE与ConfT2)的变化将改变算法在输出空间的检测样本数量,进而使待标注缓存窗口填满次数、伪真值标注次数、模型更新次数及伪真值标注精度变化,并对更新后模型RMSE 产生影响.其影响方式与可变参数w、ε变化所产生的影响相似,即改变模型对漂移的学习程度与其更新效率.

上述分析表明,可变参数的设置方式对软测量模型的最终性能具有一定影响.在选择参数时需结合实际应用背景,具体为:1) 新样本概念变化缓慢或对模型测量影响程度较小时,应设置较大缓存样本窗口容量以充分学习漂移特征,从而获取最优测量性能;反之则应设置较小缓存样本窗口容量以及时避免测量性能快速恶化;2) 当新样本的特征空间分布与历史样本接近时,应设置较小的最近邻数量以避免提取冗余差分量信息,同时设置较低的PCA控制限有利于在输出空间区分新概念样本;反之则应设置较大的最近邻数量和PCA 控制限,从而准确标注新样本伪真值并提前将其在特征空间中与历史样本区分,提高输出空间检测效率.实际上,更新后模型RMSE 变化不仅由算法中单一可变参数改变引起,还体现为上述参数的综合变化.因此,所提漂移检测算法应用于工业过程时,应设置可供交互的数据界面窗口,实时调整可变参数以获取最优检测及模型更新效果.

5 结语

针对复杂工业过程存在概念漂移、部分难测参数的真值难以及时获取问题,文中提出一种联合样本输出与特征空间的半监督概念漂移检测方法.其策略是:通过PCA 筛选特征空间内存在概念漂移的样本后,再结合TD 学习算法和Page-Hinkley 检测法,在样本输出空间进行伪真值标注并识别能够表征概念漂移的新样本.本文所提方法的创新性表现在:1) 采用联合PCA 和Page-Hinkley 检测法的策略充分反映新样本在特征空间和样本输出空间的概念漂移行为;2) 将基于TD 学习的半监督机制用于特征空间漂移样本的伪真值标注,为面向工业回归问题的半监督概念漂移检测提供了新方法;3) 采用真实MSWI 过程数据集验证了所提方法在实际应用中的可行性,并表明其具有优于已有方法的性能.

目前,面向工业回归测量领域的半监督漂移检测研究尚处于探索阶段.进一步的研究方向包括:1)为避免凭借人工经验设定模型参数导致漂移检测过程的随意性和差异性,研究模型参数的自适应选择算法;2)为提高标注的准确度,对伪真值标注算法进行改进;3)为提高概念漂移检测算法的适应性,研究针对实际工业过程的漂移理解和漂移处理策略.