金属基底上光学偶极纳米天线的自发辐射宽带增强:表面等离激元直观模型*
张炼 王化雨3) 王宁 陶灿 翟学琳 马平准 钟莹 刘海涛†
1) (南开大学电子信息与光学工程学院,现代光学研究所,天津 300350)
2) (南开大学,天津市微尺度光学信息技术科学重点实验室,天津 300350)
3) (郑州师范学院物理与电子工程学院,郑州 450044)
4) (天津大学精密仪器与光电子工程学院,精密测试技术及仪器国家重点实验室,天津 300072)
1 引言
光学纳米天线[1,2]支持表面等离激元(surface plasmon polariton,SPP),能够将电磁场限制在远小于衍射极限区域内[2,3],产生局域表面等离激元共振(localized surface plasmon resonance,LSPR),可实现远场激励下电磁场增强[4-7]或辐射源(荧光分子或量子点)激励下自发辐射增强[8-11],因此被广泛应用于生物及折射率传感[2,3],荧光增强[8,9,12-15],拉曼散射增强[16,17],单光子源[2,3,18],发光二极管[3,19],纳米激光器[20,21]及非线性增强[22,23]等方面.在过去的几十年中,由单个或耦合的纳米粒子组成的光学纳米天线,如金属纳米球[24],金属纳米立方体[16],偶极天线[1,4,25,26],蝶形纳米天线[12,26],Sierpinski 分形天线[5],环形天线[8,27,28],孔径天线(零模波导[14,15],交叉槽纳米天线[29])等,已被广泛研究.
最近,一种金属镜面上纳米颗粒(nanoparticles on mirror,NPoM)天线结构,凭借其易于制造,且形成的纳米间隙尺寸能达到纳米甚至亚纳米量级等优势,成为光学纳米天线研究的热点.该结构的纳米颗粒和金属基底之间能形成间隙表面等离激元(gap surface plasmon,GSP)[30,31],将电磁场限制在深亚波长区域内,从而突破光学衍射极限,产生极大的电磁场增强[32-35].对于在纳米间隙中放置了辐射源(荧光分子或量子点)的NPoM 结构,GSP 能获得极小的模式体积V,导致更高的Purcell 因子FP(正比于Q/V,Q是GSP 模式的品质因子)[3,32,36],从而缩短荧光寿命,可用于提升单光子源[2,3,18]、发光二极管[3,19]、纳米激光器[21]等高速纳米尺度光源的调制速度.此外,由于NPoM 纳米间隙中巨大的局域场增强能导致荧光激发速率和自发辐射速率的同时增大[37,38](后者能够提高辐射源的量子产率),从而显著提高荧光强度,这对于高亮度光源[2,3,18,19,21]、高灵敏度荧光传感[2,3,37]、表面增强拉曼散射[16,39,40]等应用有重要意义.
为了解释光学天线具有上述性能的物理机制,已经建立了一些理论模型.第一种模型将光学天线视为由电阻、电容和电感组成的等效电路[41,42],研究天线的谐振特性,然而无法得到天线的远场辐射方向图.第二种模型是基于LSPR,将纳米天线视为开放的谐振腔,将光学天线的谐振特性归因于LSPR 的激励[43-45].LSPR 可被定义为准简正模式(quasi-normal mode,QNM)[46-49],当激励源频率与QNM 的复数本征频率的实部相等时,纳米光学天线会产生谐振.上述两种模型中,均未体现SPP 的作用.为了阐明SPP 在天线谐振特性中的关键作用,建立了SPP 的Fabry-Perot 模型[50-56],把金属纳米天线看作一个 Fabry-Perot 共振腔.该模型可灵活应用于多种结构,例如,纳米棒光学天线[51,52,54]、圆形天线[56],甚至任意形状的金属纳米颗粒[53]等.然而,其中一些模型虽然能够较好地复现天线的辐射速率和远场辐射图等[51,54],但是其中某些参数是通过假设或拟合得到,缺乏严格的电磁学基础.与此不同,通过考虑天线中SPP 的激发与多重散射过程,能够建立多重散射SPP 模型,模型中所有参数都是通过Maxwell 方程组第一性原理计算获得,而无需任何假设或拟合,这保证了模型具有严格的电磁学基础,此类模型已应用到单纳米线天线[57]、偶极天线[46,58],甚至具有弯曲臂的分裂环形天线[59],能够全面预测自发辐射速率增强因子[46,58,59]、近场分布[46,57-59]和远场辐射角分布[58,59]等.
由于荧光分子或量子点的荧光光谱通常覆盖一定的波长范围[12,18],因此设计具有宽波段辐射增强性能的天线具有重要意义.在这方面,采用一种纳米线光学纳米腔,具备超小的模式体积,能提供30 nm 带宽的自发辐射速率增强(峰值FP> 6)[60].采用金纳米环-中心蝴蝶结天线[8]以及金纳米环-单蝶形尖峰天线[27],能分别在600 nm 的宽带内实现FP> 1000[8]以及在800 nm 的宽带内实现FP>450[27].采用对数周期纳米天线,通过调节尺寸参数,能实现宽频带的Purcell 因子增强[61].采用V 型槽环谐振器,能在1.0—1.8 eV 的频率范围内获得最大值高于2000 的Purcell 因子[62].采用银纳米颗粒和银膜组成的NPoM 结构,在500—1000 nm 的波长范围内自发辐射速率增强因子最大值能达到100 以上[63].采用非对称等离子体天线,由于每个臂具有不同的共振频率,也可以产生宽波段Purcell 因子增强[9].
本文提出了一种NPoM 天线结构—金属镜面上光学偶极纳米天线.该天线的总自发辐射速率增强因子(即Purcell 因子FP)能够达到5454,远场辐射速率增强因子达到1041.在近红外波段,天线能够实现宽波段自发辐射增强,FP> 1000 的波长范围达到260 nm,并且能够实现远场定向辐射.通过改变天线臂间狭缝宽度、两臂长度,能够分别调节自发辐射增强的带宽和增强因子.为了解释天线上述性能背后的物理机制,本文通过考虑沿天线臂传播的SPP 的多重散射过程,建立了SPP 半解析模型.模型中所有参数都是通过第一性原理计算获得,不需要任何拟合过程,这保证了模型具有坚实的电磁学基础,并且能够给出定量的预测.该模型能够全面复现天线的辐射特性,包括总辐射速率、远场辐射速率、远场辐射方向图等.由模型得到了能预测天线谐振的两个相位匹配条件.模型表明,在相位匹配条件下,SPP 在天线臂上形成了一对Fabry-Perot 共振获得增强,并传播到纳米间隙内点辐射源位置和散射到自由空间中,由此分别提高了总自发辐射速率和远场辐射速率;并且,这一对Fabry-Perot 共振产生了一对靠近的谐振峰,由此形成了宽波段自发辐射增强.
2 研究方法
2.1 全波数值计算方法
如图1(a)所示,本文提出一种金基底上金偶极纳米天线结构,由金基底、聚甲基丙烯酸甲酯(polymethyl methacrylate,PMMA)中间介质层及位于上方的偶极金纳米矩形天线组成,天线处于空气环境中(折射率为1).两天线臂之间的狭缝沿x方向的宽度为w,天线与金基底之间的纳米间隙沿z方向的高度为H=10 nm.设天线的两臂臂长为L,y-z横截面为正方形(边长为D=40 nm).取坐标系原点O位于金基底表面上狭缝中心位置.荧光分子或量子点辐射源采用点电流源表示,位于天线与金基底之间的纳米间隙内点S处,沿z方向偏振,该偏振方向和其他偏振方向相比能获得更高的自发辐射速率.金依赖于波长的折射率采用文献[64]中的数值.
z偏振的点电流源可以表达为电流密度J=δ(x-xs,y-ys,z-zs)z,其中δ为狄拉克函数,(xs,ys,zs)是点源的位置坐标,z为沿z向的单位矢量.取(xs,ys,zs)=(w/2+L—d,0,H/2),其中d=10 nm为点源到天线右端距离.点源的总辐射速率可表达为[58]Γtot=—Re[Ez(xs,ys,zs)]/2,其中Re[Ez(xs,ys,zs)]为点源位置电场z方向分量的实部.总辐射速率Γtot包含两部分:一部分为非辐射速率Γnr,以热的形式损耗在金属内部;另一部分为远场辐射速率Γrad,该部分能量向天线外辐射到远场,即Γtot=Γrad+Γnr.Γrad表达为Γrad=A为包含天线和点源的封闭曲面,S为点源激发的电磁场的时间平均坡印廷矢量,n为A上指向外的法向单位矢量.
为了表征自发辐射速率的增强,本文将总辐射速率增强因子(Purcell 因子[36])和远场辐射速率增强因子分别定义为γT=Γtot/ΓPMMA及γR=Γrad/ΓPMMA.其中ΓPMMA=ηvack02nPMMA/(12π),是全空间为PMMA 的均匀介质中点源的总辐射速率,ηvac为真空中的波阻抗,k0=2π/λ为真空中的波数,nPMMA=1.5 为PMMA 的折射率.为了缩短高速纳米光源(如单光子源[2,3,18]、发光二极管[3,19]和纳米激光器[21])的荧光寿命,以提高调制速率,需要高的γT值.此外,荧光强度正比于荧光发射体的量子产率,表达为η=其中η0∈(0,1)表示荧光发射体的固有量子产率.对于较高η0的发射体,即η0≈1 (例如量子点[11,18,19],或直接带隙半导体结构、可见光发射的染料分子、荧光蛋白[3]),纳米天线导致的修正后的量子产率可能会降低[3,12,63,65],表达为η≈γR/γT(称为天线辐射效率)[38,65];而对于具有极低η0的发射体,即η0≪1 (例如红外发射的染料分子、自发荧光的生物结构和硅[3]),纳米天线导致的修正后的量子产率可能会增大[3,8,27,63],表达为η≈γRη0.
为了简化分析和计算,位于点S(xs,ys,zs)振幅为1 的点源,可等效为位于点S(xs,ys,zs)和点S′(—xs,ys,zs)处,振幅均为1/2 的对称点源(如图1(b1)所示)和振幅分别为1/2 和—1/2 的反对称点源(图1(b2))的叠加,表达式为
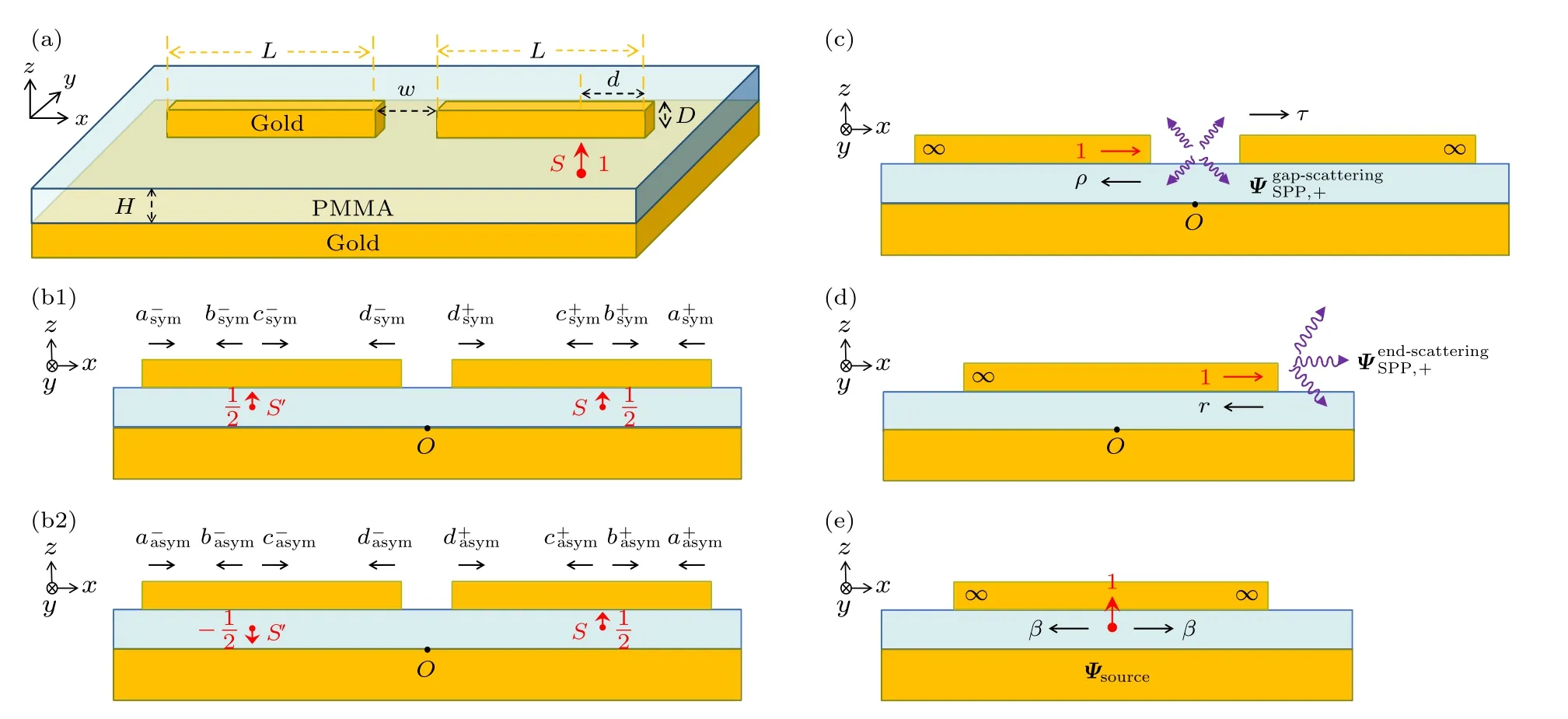
图1 (a) 金基底上金偶极纳米天线结构示意图;(b1),(b2)对称点源和反对称点源激励下,SPP模型中的SPP 模式系数的定义;(c)—(e) SPP模型中用到的SPP散射系数ρ,τ,r,β以及电磁场的定义Fig.1.(a)Schematicdiagramofthegolddipolenanoantennaona goldsubstrate;(b1),(b2) definitionof theSPPmodecoefficients in the SPPmodelunderexcitation by symmetric and anti-symmetricpointsources;(c)-(e)definitionoftheSPPscatteringcoefficie nts ρ,τ,r,βandelectromagneticfields used in the SPP model.
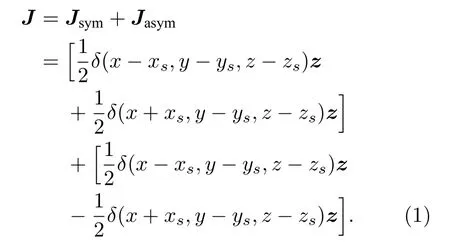
于是,单位振幅点源产生的辐射场为Ψ=Ψsym+Ψasym,其中Ψ=[E,H]表示电场(E)和磁场(H)矢量,Ψsym和Ψasym分别表示对称、反对称点源的辐射场.因此,纳米间隙中点源的总辐射速率表达为
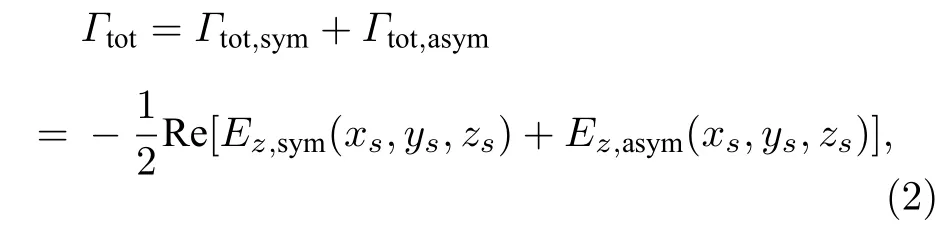
其中Ez,sym(xs,ys,zs)和Ez,asym(xs,ys,zs)分别是对称点源和反对称点源在点S(xs,ys,zs)位置激发的电场z分量.此外,利用Ψ=Ψsym+Ψasym,也可以计算远场辐射速率Γrad.为了获得天线辐射的严格数据,本文使用全波非周期傅里叶模式法(aperiodic Fourier modal method,a-FMM)[66,67].
2.2 SPP 模型
为了分析天线自发辐射增强的物理机制,接下来将考虑SPP 直观的激发和多重散射过程,建立一个半解析SPP 模型.将天线臂看成沿x方向平移不变的波导,支持沿x方向传播的SPP 波导模式.由于所有波导模式构成了一组完备的基函数[68],因此,在天线臂沿x方向的范围内(—w/2 —L≤x≤ —w/2 或w/2 ≤x≤w/2+L),点源激励的电磁场能够表达为天线臂支持的SPP 波导模式的线性叠加.由于天线截面尺寸以及天线与金基底之间的间隙尺寸远小于波长,因此只有SPP 基模式是束缚的(场沿横向y和z方向无限远处衰减为0)和传播的(传播常数几乎为实数),其他高阶模式要么是非束缚的,要么是非传播的[69].因此,对于上述电磁场表达为SPP 波导模式的线性叠加,模型中只考虑SPP 基模式,忽略其他高阶模式的贡献.图2 给出了使用全波a-FMM[66,67]计算得到的y -z横截面上SPP 基模式场分布,可见间隙中电场的主要分量为Ez.计算选取波长λ=1 µm,D=40 nm,H=10 nm,计算得到SPP 基模式的等效折射率为neff=3.4304+0.1009i.

图2 在y-z 横截面上SPP 基模式电场分量的模值(|Ex|,|Ey|,|Ez|),在(y,z)=(0,H/2)处满足归一化Ez=1.图中叠加的虚线显示了结构的边界Fig.2.Moduli of the electric-field components (|Ex|,|Ey|,|Ez|) on the y-z cross section for the fundamental SPP mode satisfying normalization Ez=1 at (y,z)=(0,H/2).The superimposed dashed lines show the boundaries of the structure.

为了求解SPP 系数,可以写出一组SPP 耦合方程:

其中u=exp(ik0neffd)是SPP 从点源传播距离d 到达天线端面时累积的相移因子,v=exp[ik0neff(L — d)]是SPP 从点源传播距离(L — d)到达狭缝时累积的相移因子,k0=2π/λ 是真空中波数,neff是SPP 模式的复数等效折射率(无量纲).ρ 和τ 分别是SPP 在天线臂间狭缝的反射和透射系数,如图1(c)所示.r 是SPP 在天线端面的反射系数,如图1(d)所示.β 是单位振幅的点源激励的SPP 系数,如图1(e)所示.这里ρ,τ,r,β 是作为散射矩阵元素[70,71],采用全波数值方法a-FM M[66,67]严格计算得到.可见,模型中用到的所有物理量都是基于Maxwell 方程组第一性原理计算获得,无需任何拟合过程,这就保证了模型具备严格的电磁学基础,并且能够给出定量的预测.此外,β 也可以采用互易定理[68]计算如下:
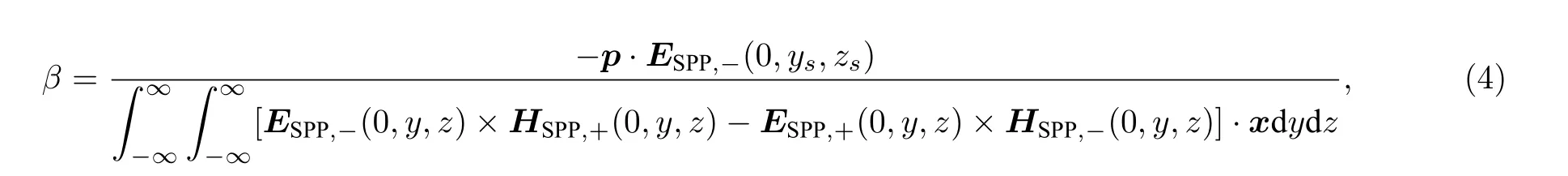
其 中ΨSPP,±(x,y,z)=ΨSPP,±(0,y,z)exp(±ik0neffx),表示沿x轴正向(+)、负向(—)传播的SPP 模式,p=z为沿点源偏振方向的单位矢量.方程(4)的优势在于,当计算得到ΨSPP,±后,如果改变点源的位置(ys,zs)或偏振方向p,不必重复求解Maxwell 方程组,即可得到β.

求解方程(3),可以分别得到对称、反对称点源激励的SPP 模式系数,即
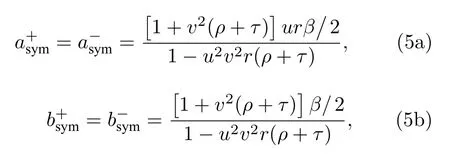
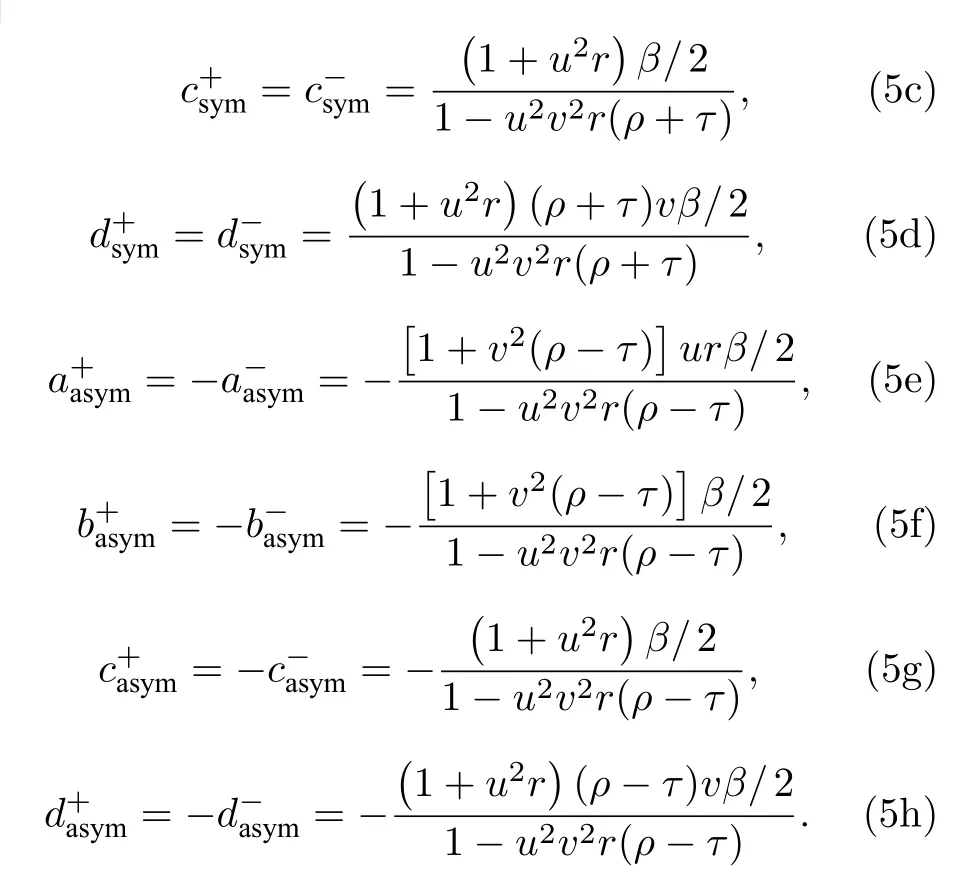
在对称、反对称点源激励下(图1(b1)和图1(b2)),天线右臂与金基底之间间隙内电磁场Ψgap,sym和Ψgap,asym可表达为
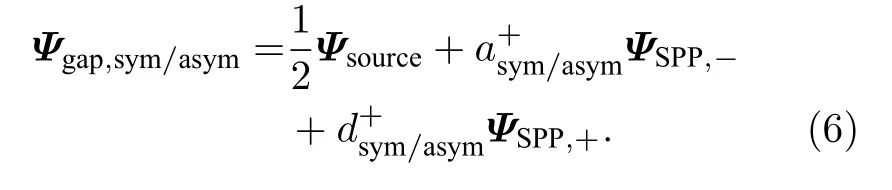
方程(6)中,Ψ=[E,H]与前文定义一致,Ψsource是振幅为1 的点源直接激发的电磁场,如图1(e)所示.ΨSPP,+和ΨSPP,—分别是前文定义的右行、左行SPP 基模式场.Ψsource,ΨSPP,+,ΨSPP,—都可以利用全波a-FMM[66,67]进行计算.于是,在单个点源激励下(图1(a)),天线右臂与金基底间的间隙内电磁场可以表达为
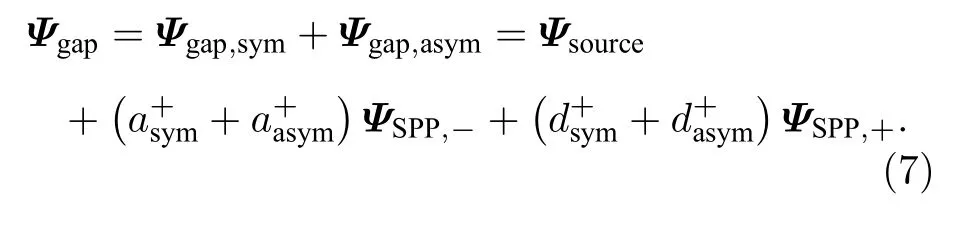
利用方程(7),即可得到间隙中点源的总自发辐射速率Γtot=— Re[Ez(xs,ys,zs)]/2.
在对称、反对称点源激励下,自由空间中的电磁场Ψsym和Ψasym可表达为

利用方程(9),即可计算远场辐射速率Γrad.
3 结果与讨论
3.1 天线的自发辐射宽带增强现象
为了研究单个点源辐射波长λ及天线臂间狭缝宽度w对天线辐射特性的影响,根据附录A 中金基底上单臂纳米天线的结果,将偶极天线臂长固定为L=Lres,1=126 nm (图3(a1)和图3(b1))及L=Lres,2=272 nm (图3(a2)和图3(b2)),绘制了归一化总自发辐射速率γT=Γtot/ΓPMMA与归一化远场辐射速率γR=Γrad/ΓPMMA随λ变化的函数曲线,其中选取不同的天线臂间狭缝宽度w=5,10,15,20,25,30,35 nm.全波a-FMM 的计算结果(圆圈)表明,在谐振峰处,偶极天线能够实现γT,γR的显著增强(γT≫1,γR≫1).例如,当L=Lres,1,w=35 nm 时,在波长λ=1.01 µm处γT,γR分别达到5454 及1041.如2.1 节所述,高的γT,γR值对于高速纳米光源[2,3,18,19,21]、表面增强荧光[8,9,12-15]或拉曼散射[16,17,39,40]等应用非常重要.在这方面,对于其他具有宽波段辐射增强性能的天线,例如,金纳米环-中心蝴蝶结天线[8]可实现最高γT≈ 2100,γR≈ 1700,金纳米环-单蝶形尖峰天线[27]可实现最高γT≈ 760,γR≈ 520,V 型槽环谐振器[62]可实现最高γT≈ 2400,非对称等离子体天线[9]可实现最高γT≈ 4500,γR≈ 1800.和上述天线相比,本文提出的偶极天线能获得更高的γT和数量级相当的γR,并且,该偶极天线属于NPoM 结构[30-35],在制备方面具有能够精确形成纳米间隙的优势.此外,本文计算的天线尺寸在实验中能够实现,已有研究可制备偶极天线臂长为几十nm[43],两臂间狭缝宽度达到5 nm[25].对于实验制备偶极天线可能出现的棱边、棱角圆角化,附录B中的计算结果表明,天线圆角化只会导致谐振波长移动,对γT和γR发生增强的带宽及其在谐振峰位置的数值影响很小.
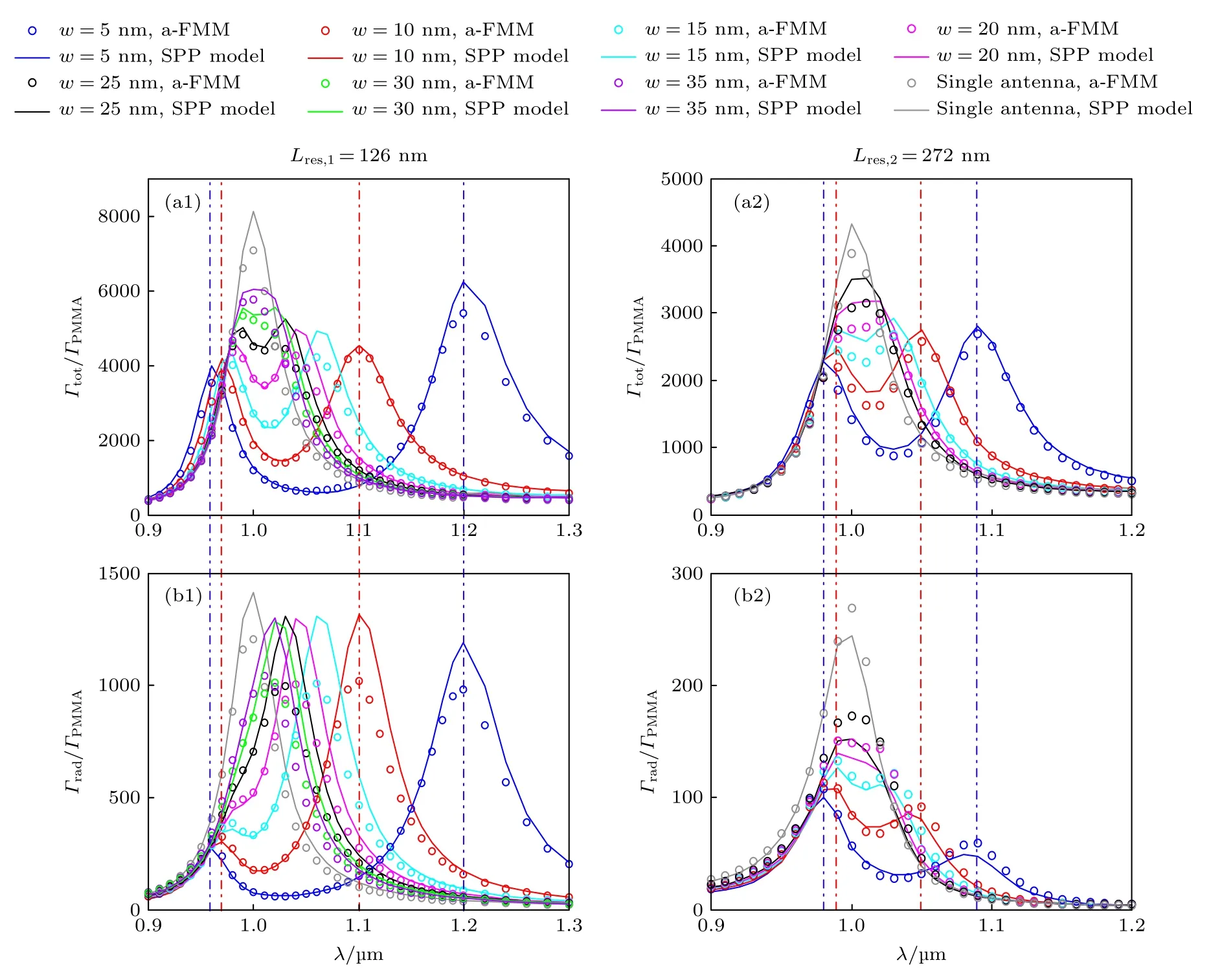
图3 在单个点源激励下,偶极纳米天线的归一化总辐射速率Γtot/ΓPMMA((a1),(a2))和归一化远场辐射速率Γrad/ΓPMMA((b1),(b2)),显示为点源辐射波长λ 的函数.结果分别采用a-FMM 严格计算(圆圈)和SPP 模型(实线)得到.(a1),(b1)天线臂长L=Lres,1=126 nm.(a2),(b2) L=Lres,2=272 nm.不同天线臂间狭缝宽度w 对应不同颜色的曲线.灰色曲线对应单臂纳米天线的结果.竖直点划线显示了方程(10)预测的谐振波长Fig.3.Normalized total emission rate Γtot/ΓPMMA ((a1),(a2)) and normalized radiative emission rate Γrad/ΓPMMA ((b1),(b2)) of the dipole nanoantenna under a single point-source excitation plotted as functions of the excitation wavelength λ.The results are obtained with the rigorous a-FMM calculation (circles) and the SPP model (solid curves),respectively.(a1),(b1) Antenna arm length L=Lres,1=126 nm.(a2),(b2) L=Lres,2=272 nm.Different widths w of the slit between the antenna arms correspond to curves of different colors.The gray curves show the results of a single-arm nanoantenna.The vertical dash-dot lines show the resonant wavelengths predicted by Equation (10).
值得注意的是,图3 显示出成对、可调的共振峰,由此产生自发辐射速率的宽带增强现象.对于图3(a1)和图3(b1)中L=Lres,1的天线,γT,γR的谐振峰总是成对出现.随着狭缝宽度w的增大,双谐振峰逐渐接近,当继续增大w时,双峰逐渐演变成单峰,且越来越尖锐,趋于单臂纳米天线的结果.当w从10 nm 增大到35 nm 时,γT> 1000 的波长范围可由[932,1200] nm 连续变化到[938,1100]nm.与γT类似,也可以通过改变w来连续调节γR获得增强的波长范围.将左、右谐振峰的谐振波长分别记为λres,1,λres,2,可以发现γT,γR谐振峰的谐振波长一致.例如,在图3(a1)和图3(b1)中,用两条竖直蓝色(或红色)点划线标出了w=5 nm(或w=10 nm)时,γT及γR双谐振峰的谐振波长,分别为λres,1=0.96 µm,λres,2=1.20 µm (或λres,1=0.97 µm,λres,2=1.10 µm),其物理机制将在下一节讨论.当w=10 nm 时,在λres,2=1.10 µm位置,天线辐射效率为γR/γT=22.95%,表明天线具有较好的远场辐射性能.对图3(a2)和图3(b2)中L=Lres,2的天线,γT,γR也出现了与L=Lres,1的天线类似的双谐振峰.当w从10 nm 增大到25 nm 时,γT> 1000 的波长范围可由[960,1090] nm连续变化到[962,1060] nm.当w=10 nm 时,在谐振波长λres,1=0.99 µm 位置,天线辐射效率为γR/γT=4.92%.对于相同的w取值,天线臂长度从L=Lres,1增大到L=Lres,2,γT与γR的峰值及获得增强的带宽均明显减小,并且在谐振波长位置,天线的辐射效率明显下降.
3.2 天线自发辐射增强特性基于SPP 模型的机理分析
为了揭示数值结果背后的物理机制,我们使用SPP 模型来预测γT与γR.如图3 所示,SPP 模型预测(实线)与全波a-FMM 计算(圆圈)结果符合较好,这证实了模型的有效性.然而,在谐振峰附近,SPP 模型存在一定的误差.该误差表明,除了模型中考虑的SPP 基模式以外,模型中忽略的其他高阶模式(非束缚态模式、非传播模式)[68,69]也对天线辐射有贡献.

其中arg()表示辐角;k0=2π/λ是真空中波数;M,N取整数,分别是对称、反对称点源激励下的谐振级次.方程(10)由方程(5)分母模值|1—u2v2r(ρ±τ)|取极小值得到,这要求arg[u2v2r(ρ±τ)]取2π 的整数倍(即方程(10)),以及|u2v2r(ρ±τ)|=|uv|2|r||ρ±τ| ≈ 1,后者基于以下考虑得到.首先,SPP 反射、透射系数ρ和τ需要满足相干形式的能量守恒关系[72],即|ρ+τ| ≈ 1,|ρ—τ| ≈ 1(当w=10 nm,λ=1 µm 时,|ρ+τ|=0.9939,|ρ—τ|=0.9676);其次,SPP 在天线两端的反射较强,即|r| ≈ 1(当λ=1 µm 时,|r|=0.9793);再次,结构中支持的SPP 为传播模式,其等效折射率neff虚部很小(λ=1 µm 时,neff=3.4304+0.1009 i),从而使得SPP 传播一个天线臂距离的衰减|uv|=exp[—k0Im(neff)L] ≈ 1.
方程(10)可用于确定发生自发辐射增强时的天线参数.例如,对于方程(10a),可写成超越方程λ=f(λ)的形式,其中
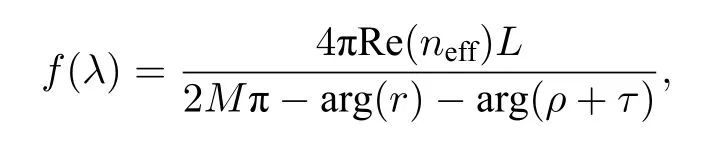
neff,r,ρ,τ均为波长λ的缓变函数.该超越方程可通过线性插值迭代法[73,74]求解,得到λ=λres,sym,为对称点源激励下的谐振波长.用同样的方法可求解方程(10b),确定λ=λres,asym,为反对称点源激励下的谐振波长.
如图4 所示,利用方程(10),预测了不同狭缝宽度w对应的谐振波长λres,sym/asym,预测结果与图3 中a-FMM[66,67]严格计算结果吻合(有λres,sym=λres,1,λres,asym=λres,2),这证实了模型方程(10)的有效性.图4 表明,有λres,sym<为金基底上单臂纳米天线的谐振波长,如图4 中水平黑色点划线所示(由附录A 中方程(A5)确定),黑色点划线上方为偶极天线在反对称点源激励下的谐振波长λres,asym,下方为偶极天线在对称点源激励下的谐振波长λres,sym.随着w增大,λres,sym与λres,asym逐渐靠近,并逐渐趋于,使得发生自发辐射增强的带宽减小,这与图3 所示结果一致.以上结果可解释如下.随着w增大,狭缝处SPP 的透射系数τ趋于0,反射系数ρ趋于SPP在天线端面的反射系数r(如图1(c)和图1(d)所示),这使得方程(10)中arg(ρ+τ)与arg(ρ—τ)均趋于相同的数值arg(r),于是方程(10)趋于单臂纳米天线的谐振条件(附录A 中方程(A5)),这使得λres,sym和λres,asym均趋于
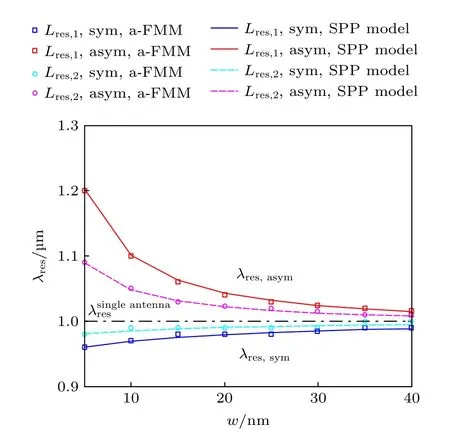
图4 偶极纳米天线谐振波长λres 随狭缝宽度w 变化的曲线.图中λres,sym=λres,1,λres,asym=λres,2,λres,1,λres,2 为图3 中γT 或γR 的谐振波长.方形、圆圈为a-FMM 严格计算结果.实线、虚线为SPP 模型方程(10)预测的结果.红色、蓝色曲线对应天线臂长L=Lres,1=126 nm [对应方程(10)中M=N=1],洋红、青蓝色曲线对应L=Lres,2=272 nm(对应M=N=2).水平点划线为方程(A5)预测的单臂纳米天线的谐振波长Fig.4.Resonant wavelength λres of the dipole nanoantenna plotted as a function of the slit width w.There are λres,sym=λres,1 and λres,asym=λres,2,with λres,1 and λres,2 being the resonant wavelengths of γT or γR shown in Figure 3.The squares and circles show the results obtained with the rigorous a-FMM calculation.The solid and dashed curves show the predictions of the SPP model Equation (10).The red and blue curves correspond to the antenna arm length L=Lres,1=126 nm (obtained for M=N=1 in Equation(10)).The magenta and cyan curves correspond to L=Lres,2=272 nm (obtained for M=N=2).The horizontal dash-dot line shows the resonant wavelength of the single-arm nanoantenna predicted by Equation (A5).
下面基于SPP 模型方程,解释天线产生谐振并引起自发辐射增强的原因.首先,当预测谐振条件的方程(10)得到满足时,SPP 沿天线臂往返传播一周所累积的相移(方程(10)左侧)为2π 的整数倍,这使得经过多重散射后的SPP 产生相长干涉叠加,从而形成SPP 的Fabry-Perot 共振.然后,根据方程(7),这些共振激发的SPP(具有较大系数)将增强点辐射源位置的电场,最终增大总自发辐射速率Γtot,如图3(a1)和图3(a2)所示.对于远场辐射速率Γrad,根据方程(9),这些共振激发的SPP(具有较大系数会增强其产生的散射场,并最终增强Γrad,如图3(b1)和图3(b2)所示.
图3 显示了随着天线臂长L的增大,发生谐振时γT,γR的峰值减小.为了解释该现象,发生谐振时,方程(5)给出的SPP 系数的分母模值满足:

其中Im()表示虚部.当L增大时,方程(11)右端增大,使得SPP 系数减小,进而使得γT,γR均减小.
3.3 近场分析
图5 显示了在单个点源激励下,采用全波a-FMM[66,67]严格计算得到的偶极天线发生谐振时的近场分布.该结果对应图3(或图4)中天线臂长度L=Lres,1及L=Lres,2,狭缝宽度w=10 nm,以及谐振波长λres,1,λres,2(或λres,sym=λres,1,λres,asym=λres,2,分别对应对称、反对称点源激励下的M,N谐振级次,见方程(10)).图5(a1)和图5(c1)表明,对于对称谐振级次(M=1,2),Re(Ez)关于x=0呈对称分布.图5(b1)和图5(d1)表明,对于反对称谐振级次(N=1,2),Re(Ez)关于x=0呈反对称分布.这可以通过SPP 模型来理解.该模型预测,在谐振条件(方程(10a))下,单个点源中包含的对称点源激发的场产生谐振(即方程(5b)—(5d)给出的对称点源激发的SPP 系数取极大值),因此强于单个点源中包含的反对称点源激发的场,这使得对称点源激发的场成为电磁场的主要成分,于是电磁场显示出和对称点源一致的对称性(如图5(a1)和图5(c1)所示).同理,在谐振条件(方程(10b))下,电磁场将显示出和反对称点源一致的对称性(如图5(b1)和图5(d1)所示).图5(a2)—(d2)显示了|Ez|近场分布,其中在点源对应的(x,y)坐标位置出现了一个亮点,这是由于点源位置Im(Ez)存在趋于无穷大的奇异性.
基于激光扫描(LiDAR)和同步定位与制图(SLAM)技术能够精确地采集室内外三维激光点云数据,而不依赖GPS或使用复杂的惯导系统。使用SLAM算法,通过三维激光扫描实现地图的建立。在仪器通过时,不间断地采集精细的二维地图数据,并记录光学数据以及LiDAR的时间位置信息,然后根据光学数据建立彩色三维点云数据,将二维平面视图转换为三维立体环境。在数据采集过程中,可实时观察采集数据的质量,并能指导数据现场采集工作,避免采集过程中出现遗漏、错误等情况,确保一次性完成数据采集,提高了工作效率。

图5 单个点源激励下,天线纳米间隙内(z=H 下1 nm 截面上)主要电场分量Ez 的近场分布 (a1),(a2),(b1),(b2) 天线臂长L=Lres,1=126 nm,λres,sym=0.97 µm,λres,asym=1.10 µm (分别对应方程(10)中M=1 和N=1);(c1),(c2),(d1),(d2) L=Lres,2=272 nm,λres,sym=0.99 µm,λres,asym=1.05 µm (分 别对应M=2 和N=2);(a1)—(d1) 显示了Re(Ez);(a2)—(d2) 显示了|Ez|.Ez 做了归一化(除以ΓPMMA)Fig.5.Near-field distribution of the main electric-field component Ez in the antenna nanogap (on the cross-section of 1 nm below z=H) under excitation by a single point source:(a1),(a2),(b1),(b2) For antenna arm length L=Lres,1=126 nm and wavelengths λres,sym=0.97 µm,λres,asym=1.10 µm (respectively corresponding to M=1 and N=1 in Equation (10));(c1),(c2),(d1),(d2) for L=Lres,2=272 nm and λres,sym=0.99 µm,λres,asym=1.05 µm (respectively corresponding to M=2 and N=2);(a1)-(d1)show Re(Ez);(a2)-(d2) show |Ez|.Ez is normalized (divided by ΓPMMA).
图5 表明,随着谐振级次增大(M或N从1 增大到2),天线单臂上的驻波振幅极大值点数量增加(从2 个增加到3 个),并且场逐渐变弱.这也可以通过SPP 模型来理解.驻波源于天线臂上两个反向传播SPP 的叠加,当谐振级次增大时,相应的天线臂长增大(见方程(10)),使得驻波振幅极大值点个数增多.同时,根据方程(11),随着发生谐振时天线臂长L增大,SPP 模式系数减小,使得纳米间隙中电磁场Ψgap(方程(7))减弱,这与模型预测的总自发辐射速率Γtot的降低一致(见图3).
3.4 远场辐射角分布
图6 给出了在图3(a1)和图3(b1)的谐振波长位置,天线的远场辐射角分布P(θ,ϕ)=|S(r,θ,ϕ)|/SPMMA.其中|S(r,θ,ϕ)|是以点辐射源为中心、半径r≫λ、在空气区域半球面上的时间平均坡印亭矢量的模.θ和ϕ分别为极角和方位角.SPMMA=ΓPMMA/(4πr2)是位于均匀PMMA 环境中的点源在半径为r的球面上的平均能流密度.当r→∞时,P(θ,ϕ)将渐近地与r无关.S(r,θ,ϕ)采用近场-远场变换方法[75]计算得到.该方法需要利用包围天线和点源的一个封闭曲面上的电磁场,后者可利用全波a-FMM[66,67](第1,3 列)或SPP模型方程(9)(第2,4 列)计算得到.结果表明,对于不同的狭缝宽度w=5,15,35 nm,在谐振波长λres,sym,λres,asym位置(对应谐振级次M=1(第1,2 列),N=1(第3,4 列)),SPP 模型与a-FMM 结果吻合,验证了模型的有效性.
下面考察谐振级次及狭缝宽度w对天线远场辐射角分布P(θ,ϕ)的影响.图6 表明,远场辐射角分布强烈地依赖于谐振级次,这是由于天线远场辐射特性由近场分布决定[51,59],后者由反向传播的SPP 的驻波形成,其分布强烈依赖于谐振级次(如图5 所示).随着w的增大,对于M=1 谐振级次,P(θ,ϕ)极大值的个数由2 个减少为1 个(右侧极大值逐渐消失),最终P(θ,ϕ)极大值位置位于(θ,ϕ)=(47°,180°).对于N=1 谐振级次,随着w的增大,P(θ,ϕ)极大值的个数始终只有一个,P(θ,ϕ)极大值的位置从(θ,ϕ)=(3°,180°)逐渐偏移到(θ,ϕ)=(25°,180°),逐渐接近M=1 级次的P(θ,ϕ)(同时谐振波长λres,asym接近λres,sym),其原因见图4 结果的模型分析.对比M=1 和N=1谐振级次的P(θ,ϕ),可见后者数值更大,并且具有更好的定向辐射特性,即能够在一定的物镜数值孔径(NA=sinθ)对应的中心角区(极角θ≤60°)内取较大的数值.这有利于提高物镜的荧光收集效率,从而提高收集的荧光强度,对表面增强荧光[8,9,12-15]或拉曼散射[16,17,39,40]、超亮及高速光源[2,3,18,19,21]等应用有重要意义.
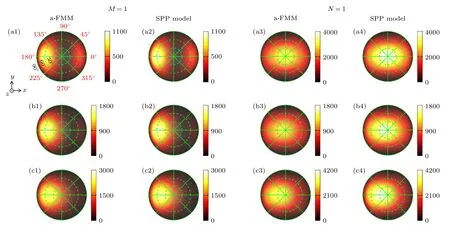
图6 在单个点源激励下,偶极纳米天线的远场辐射角分布P(θ,ϕ).计算选取图4 中天线臂长L=Lres,1=126 nm,以及不同的天线臂间狭缝宽度w 对应的谐振波长λres,sym(第1,2 列),λres,asym(第3,4 列) (a1)—(a4) w=5 nm,λres,sym=0.96 µm,λres,asym=1.2 µm;(b1) —(b4) w=15 nm,λres,sym=0.98 µm,λres,asym=1.06 µm;(c1)—(c4) w=35 nm,λres,sym=0.99 µm,λres,asym=1.02 µm.叠加的圆和径向线分别对应极角θ 和方位角ϕFig.6.Angular distributions P(θ,ϕ) of the far-field emission for the dipole nanoantenna under excitation by a single point source.The calculations are for antenna arm length L=Lres,1=126 nm and resonance wavelengths λres,sym (columns 1 and 2) and λres,asym(columns 3 and 4) corresponding to different widths w of the slit between the antenna arms (as shown in Fig.4).(a1)-(a4) w=5 nm,λres,sym=0.96 µm,λres,asym=1.2 µm;(b1)-(b4) w=15 nm,λres,sym=0.98 µm,λres,asym=1.06 µm;(c1)-(c4) w=35 nm,λres,sym=0.99 µm,λres,asym=1.02 µm.The superimposed circles and radial lines correspond to the polar angle θ and azimuth angle ϕ,respectively.
4 结论
本文提出了一种具有宽波段自发辐射增强性能的金属基底上光学偶极纳米天线.全波数值计算结果表明,对于位于纳米间隙内的辐射源,该天线的总辐射速率与远场辐射速率增强因子分别达到5454 和1041(对应天线辐射效率19.09%).在近红外波段,自发辐射增强(Purcell 因子超过1000)的波长范围达到260 nm.通过改变天线臂间狭缝宽度、两臂长度,能够分别调节自发辐射增强的带宽和增强因子,便于设计.该天线能够在一定的物镜数值孔径对应的中心角区(极角θ≤ 60°)内获得较强的远场辐射,从而提高物镜收集的荧光强度.并且,该天线属于NPoM 结构,具有能够精确形成纳米间隙的优势.基于上述性能,该天线能够为荧光分子或量子点(其荧光光谱覆盖一定的波长范围)提供宽波段的自发辐射增强,对于高速及高亮度纳米光源、高灵敏度荧光分子传感等相关应用具有重要意义.
为了阐明天线自发辐射增强性能背后的物理机制,本文考虑天线臂上SPP 激发和多重散射的直观物理过程,建立了一个半解析模型.该SPP 模型中所有参数都是基于Maxwell 方程组第一性原理计算获得,不需要任何拟合过程,这保证了模型具有坚实的电磁学基础,能够给出定量的预测.模型能够全面复现天线的辐射特性,包括总辐射速率、远场辐射速率、远场辐射方向图等.由模型得到了两个相位匹配条件,其能够预测天线发生谐振时的参数,表明在此条件下,SPP 在天线臂上形成一对Fabry-Perot 共振获得增强,该增强的SPP传播到纳米间隙内点源位置或散射到自由空间中,由此分别提高了总自发辐射速率或远场辐射速率.并且,这一对Fabry-Perot 共振产生了一对相互靠近的谐振峰,由此形成了宽波段自发辐射增强.
附录A 单臂纳米天线的自发辐射增强特性与偶极天线臂长的确定
为确定正文中偶极天线的臂长,这里考虑如图A1(a)所示的金基底上单根矩形金纳米线构成的光学天线(下文简称为“单臂纳米天线”).设单位系数z偏振点源位于(xs,ys,zs)=(L/2 —d,0,H/2),取坐标原点O位于金基底表面上天线中心位置.d,H,天线尺寸,折射率等的取值与正文偶极天线相同.取波长λ=1 µm,计算了归一化总辐射速率γT=Γtot/ΓPMMA和归一化远场辐射速率γR=Γrad/ΓPMMA随天线臂长L变化的曲线,如图A1(c)所示.a-FMM[66,67]严格计算结果表明(蓝色、红色圆圈分别显示了γT,γR),γT与γR呈现准周期谐振峰,前2 个峰值位置为Lres,1=126 nm,Lres,2=272nm.在谐振峰位置,γT与γR均显著增强(γT≫1,γR≫1),并且峰值数值随L增大逐渐下降,最大峰值出现在L=Lres,1,此时有γT=7089,γR=1574.
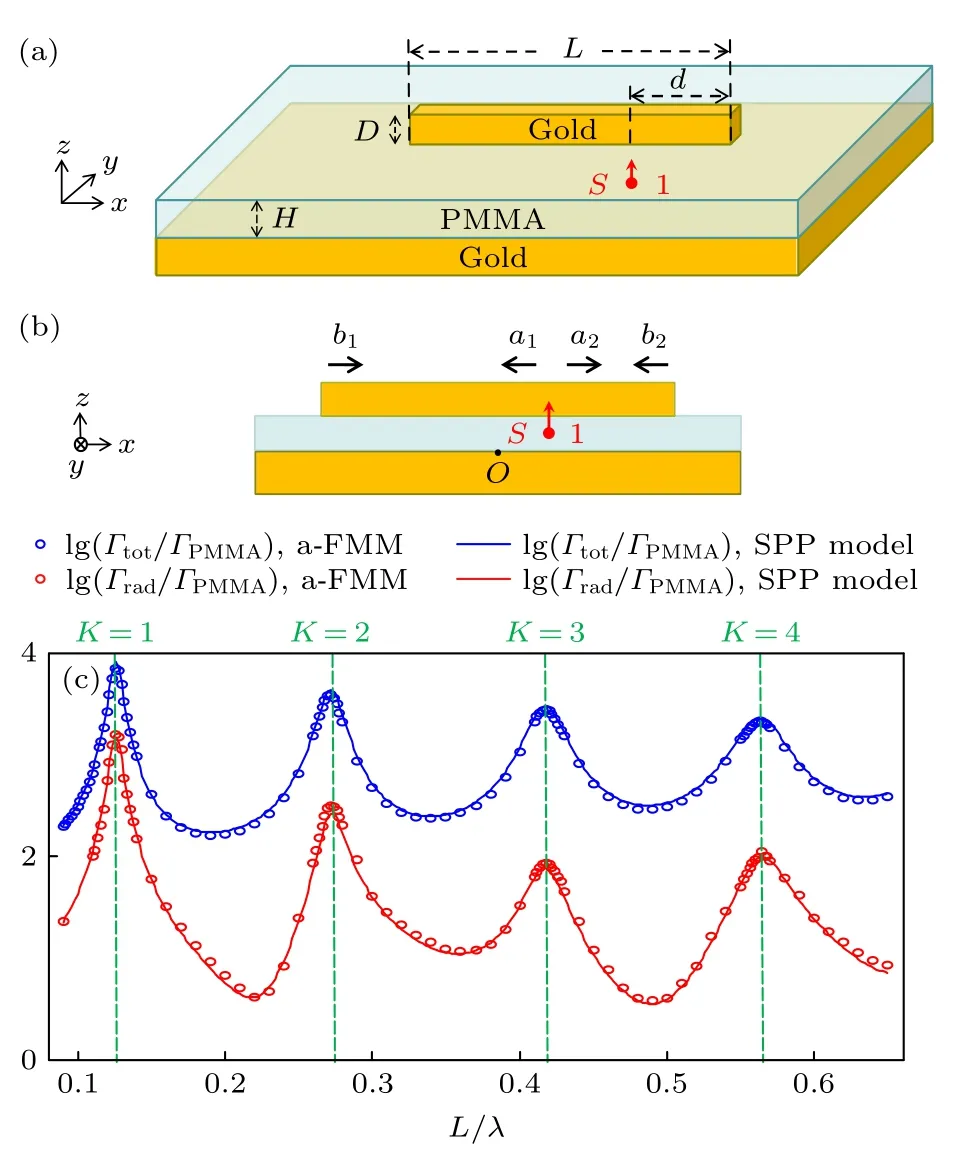
图A1 (a) 金基底上单臂纳米天线示意图;(b) 在单个点源激励下,SPP 模型中SPP 模式系数a1,a2,b1,b2 的定义;(c) 归一化总辐射速率Γtot/ΓPMMA(蓝色曲线)和归一化远场辐射速率Γrad/ΓPMMA(红色曲线)随天线臂长L 变化的曲线(固定波长λ=1 µm).圆圈和实线分别为全波a-FMM,SPP 模型的结果.竖直绿色虚线显示了方程(A5)确定的发生谐振的LFig.A1.(a) Schematic diagram of a single-arm nanoantenna on a gold substrate;(b) definition of the SPP mode coefficients a1,a2,b1,b2 in the SPP model under a single point-source excitation;(c) normalized total emission rate Γtot/ΓPMMA (blue curves) and normalized radiative emssion rate Γrad/ΓPMMA (red curves) of the antenna plotted as functions of the antenna arm length L (for fixed wavelength λ=1 µm).The circles and solid curves show the results of the full-wave a-FMM and SPP model,respectively.The vertical green dashed lines show the L at resonance determined by Equation (A5).
为了解释数值结果,下面建立SPP 模型来预测γT,γR,模型的建立过程与偶极天线类似.图A1(b)给出了模型中的SPP 模式系数,其中a1,a2分别是由点源出发向天线左端、右端传播的SPP 系数,b1,b2是由天线左端、右端出发向点源传播的SPP 系数.为了确定SPP 系数,可以列出一组SPP 耦合方程:


于是,单臂纳米天线与金基底之间的间隙内电磁场Ψgap及自由空间中的电磁场Ψrad可表达为
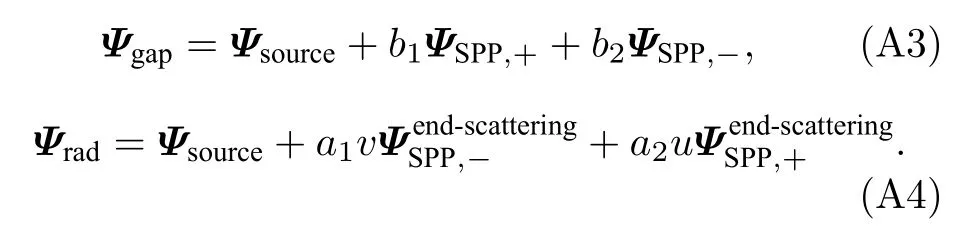
方程(A3)和(A4)中,电磁场Ψsource,与波导模式场ΨSPP,±的定义和计算方法与偶极天线相同(见正文方程(6)和方程(8)后).得到Ψgap,Ψrad后,即可分别用于计算总辐射速率Γtot和远场辐射速率Γrad.如图A1(c)所示,SPP 模型(实线)与全波a-FMM(圆圈)计算得到的Γtot(蓝色曲线),Γrad(红色曲线)吻合,验证了模型的有效性.此外,值得注意的是,当改变天线长度L、点源到天线右端距离d时,SPP 模型的执行不必重复求解Maxwell 方程组(这是由于SPP 模型方程对L,d的依赖关系是解析化的,见方程(A2)),而全波a-FMM[66,67]的执行需要重复求解Maxwell 方程组,因此,SPP 模型具有更高的计算效率.这一点对于正文中偶极纳米天线的SPP 模型也是成立的.与正文方程(10)类似,对于单臂纳米天线,Γtot和Γrad取极大值要求SPP 系数取极大值,进而要求方程(A2)分母的模值取极小值,可得如下相位匹配条件:

其中K取整数,对应不同的谐振级次.对比方程(10)和方程(A5),可见前者取τ=0,ρ=r即成为后者,原因是偶极天线取天线臂间狭缝尺寸w→∞即成为单臂纳米天线.利用方程(A5),对于固定的波长λ,有k0=2π/λ,neff,r均与天线臂长L无关,于是可确定天线发生谐振时的臂长L=Lres.方程(A5)确定的Lres(取K=1,2,3,4)如图A1(c)中的竖直绿色虚线所示,可见能准确预测谐振峰的位置,验证了方程(A5)的有效性.与正文方程(10)类似,方程(A5)的物理含义为,SPP 沿天线往返传播一周所产生的相移(方程(A5)左侧)为2π 的整数倍,使得多重散射的SPP 发生相长干涉叠加,由此形成了SPP 的Fabry-Perot 共振.
固定波长λ=1 µm 时,基于图A1(c)中的a-FMM 严格计算结果或SPP 模型方程(A5),即可确定前2 个谐振峰对应的单臂纳米天线长度Lres,1=126 nm,Lres,2=272 nm(对应K=1,2),这作为正文第3 节的计算中偶极天线的天线臂长度.由此可以预期,当偶极天线的天线臂间狭缝尺寸w→∞时,偶极天线趋于单臂纳米天线,则偶极天线的谐振波长必然趋于1 µm,如正文图3 和图4 所示.
附录B 棱边、棱角圆角化对偶极天线性能的影响
对于实验制备偶极天线可能出现的棱边、棱角圆角化,其对偶极天线性能的影响将在这里讨论.如图B1 所示,天线棱边、棱角圆角化分别采用与矩形表面相切的圆柱面、球面,设其半径为R.图B2 给出了R=2,4,6 nm 时(粉色、青色、蓝色曲线),偶极天线的归一化总辐射速率γT=Γtot/ΓPMMA(图B2(a))和归一化远场辐射速率γR=Γrad/ΓPMMA(图B2(b))随点源辐射波长λ变化的曲线.计算采用有限元法(finite element method,FEM),使用商用软件COMSOL Multiphysics 执行.计算固定天线臂长L=Lres,1=126 nm,臂间狭缝宽度w=10 nm.图B2 中R=0 (红色曲线)为无圆角化时,全波a-FMM 的计算结果(即图3(a1)和图3(b1)中红色圆圈曲线).结果表明,随着圆角化半径R增大,γT,γR的谐振波长减小,然而,γT,γR发生增强的带宽及其在谐振峰位置的数值变化很小.
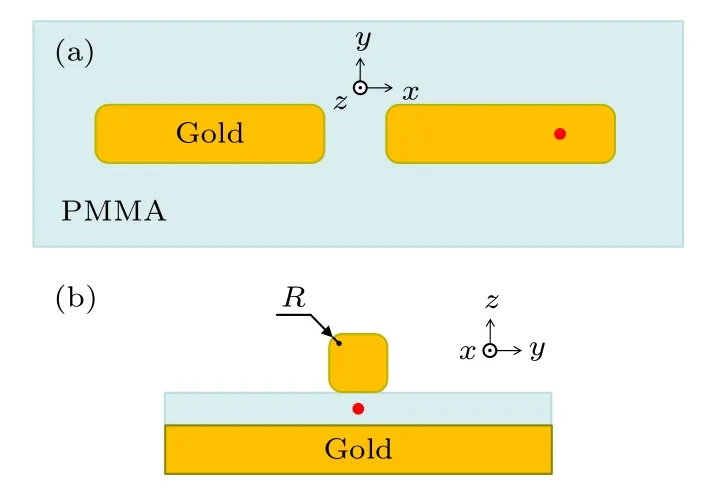
图A1 偶极天线棱边、棱角圆角化后的俯视图(a)、侧视图(b).图中红点代表辐射点源Fig.B1.Top view (a) and side view (b) of the dipole antenna with rounded edges and corners.The red dot represents the emission point source.
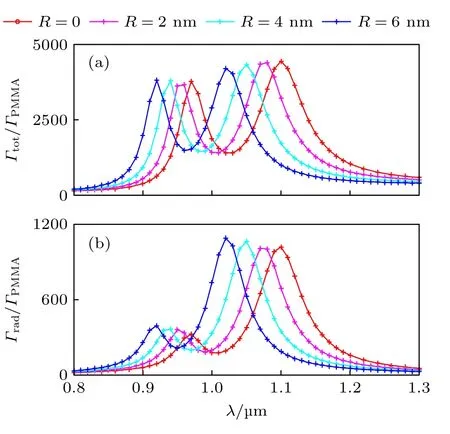
图A2 对于不同圆角化半径R 的偶极天线(对应不同颜色的曲线),在单个点源激励下,归一化总辐射速率Γtot/ΓPMMA (a)和归一化远场辐射速率Γrad/ΓPMMA (b)随波长λ 变化的曲线.计算采用a-FMM(红色曲线)和FEM(粉色、青色、蓝色曲线).选取天线臂长L=Lres,1=126 nm,臂间狭缝宽度w=10 nmFig.B2.For the dipole antenna with different radii R of rounded edges and corners (corresponding to curves of different colors),the normalized total emission rate Γtot/ΓPMMA (a) and normalized radiative emission rate Γrad/ΓPMMA (b) under excitation by a single point source,which are plotted as functions of wavelength λ.The calculation is performed with the a-FMM (red curves) and the FEM (pink,cyan,and blue curves).The antenna arm length is L=Lres,1=126 nm,and the width of the slit between the antenna arms is w=10 nm.

