一类复合函数求导的两种解法
□胡梦薇
一、引言
在高职院校高等数学教学中,经常会遇到计算有关一类复合函数形式
y=eu(x)
(1)
的导数问题,这里u(x)是初等函数,教材中最常用的方法是复合函数求导法则,运用此种方法解决求导问题的关键是要对复合函数进行合理分层,虽然此种方法能够解决大部分复合函数的求导问题,但是对于某些复合函数分层比较复杂的情况就需要寻找简便方法。
对于(1)中的复合函数,选取通式y=esin(axn+b)为研究对象,发现学生在做题的过程中经常由于分层不清楚的问题,导致计算错误。鉴于此,本文采用对数求导法,对数求导法是一种利用对数的性质与隐函数的求导法则来简化导数计算的方法,使用这种方法来解决形如(1)式的显函数的导数问题,不仅减少了复合函数分层的麻烦,也有利于训练学生的思维能力,提高解题思路的灵活性。
本文推广研究了如下形式
y=esin(axn+b)
(2)
的复合函数,这里a、b是常数,n∈R。
二、准备知识
定义2.1[1]幂函数y=xa(a为任何实数);指数函数y=ax(a>0,且a≠1);对数函数y=logax(a>0,且a≠1);三角函数y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx及反三角函数y=arcsinx,y=arccosx,y=arctanx等五类函数统称为基本初等函数。
定义2.2[1]如果一个函数可用一个式子表示,且这个式子是由常数及基本初等函数经过有限次四则运算与有限次复合构成的,则这类函数统称为初等函数。
定义2.3[1]设D是平面上的一个点集,如果对于每一组数(x,y)(或称点P(x,y)),变量z按一定规则f,都对应着唯一一个确定的值,则称变量z是变量x,y的二元函数,或称为点P的函数,记作
z=f(x,y)或z=f(P)
x,y称为自变量,z称为因变量,D称为函数z=f(x,y)的定义域。
定义2.4[2]设函数y=f(u)和u=φ(x),且u=φ(x)的值域或部分值域包含在f(u)的定义域中,则通过u,y与x建立了对应关系,记为y=f[φ(x)],称此函数是由函数y=f(u)和u=φ(x)复合而成的复合函数,其中u称为中间变量。
定义2.5[2]在实际问题中,有时还会遇到用一个方程表示函数关系的情形,例如方程x2+y2=a2确定着y与x之间的函数关系。一般地,由一个二元方程F(x,y)=0所确定的函数y=f(x)称为隐函数。
定义2.6[2]设函数y=f(x)在点x0的某领域内有定义,当自变量x在点x0处有增量Δx时(点x0+Δx仍在该领域内),相应地函数有增量
Δy=f(x0+Δx)-f(x0)
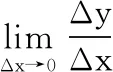
也可以记作

定义2.7[1]设函数z=f(x,y)在点P(x0,y0)的一个领域内有定义,如果
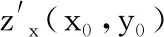
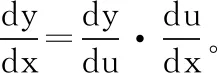
定理2.2[2](隐函数求导)把由F(x,y)=0所确定隐函数y=y(x)代入原方程,得到恒等式
F(x,y(x))=0
运用复合函数求导法,在等式两端对x求导,得到一个含y′的方程,解出y′,即为所求隐函数的导数。
三、问题解决的两种方法
方法一,复合函数求导法[1]
解 函数y=esin(axn+b)可以看作由y=eu,u=sinv,v=axn+b复合而成,运用复合函数求导法,得
一方面加强理论培训。通过培训让组织者进一步掌握中央重大决策部署,提高宣传、团结、发动群众和组织基层宣传的能力。另一方面对组织者采取“请进来、走出去”的方式提升理论素养、业务素质和工作能力,有计划分批次选派人员到机关跟班学习。
y′=(eu)′·(sinv)′·(axn+b)′
=eu·cosv·naxn-1
=naxn-1·cos(axn+b)·esin(axn+b)
因为u和v是假设的中间变量,所以求导结束之后一定要记得回代,消去中间变量u和v。可以看出,运用复合函数求导法对此函数进行分层求导时,并且容易因为复合函数分层的问题而出现计算错误,所以需要尝试其他更简洁的方法。由于受到隐函数求导思想和对数函数性质的启发,给出下面的第二种解法。
方法二,对数求导法
解 等式两边取对数,得
lny=sin(axn+b)
方程两边同时对x求导,得
即
y′=cos(axn+b)·naxn-1·y
=naxn-1·cos(axn+b)·esin(axn+b)
通过上面的解题过程可以看出,这个方法降低了对复合函数分层的要求,减少了求导次数,提高了解题的正确率。
此方法的解题步骤总结如下:
(1)函数等式的两边取对数;
(2)等式两边对x求导,并且注意到y是x的函数;
(3)解出y′,并把y关于x的函数表达式代入,得到所求的结果。
上面的方法对求多元函数的偏导数同样适用,我们以二元函数为例进行说明。
例 求函数z=esin(axn+bym),a、b是常数,n,m∈R
解 等式两边取对数,得
lnz=sin(axn+bym)
方程两边同时对x求偏导,得
即

=naxn-1·cos(axn+bym)·esin(axn+bym)
四、结语
本文完整、详细地研究了形如(1)式的复合函数求导的两种计算方法,通过对比可以看出使用对数求导法计算,能够避免因为复合函数分层而容易出现的错误。另外,此题的结果可以作为一个通项公式来用,提高此类题目的解题效率。

