图书利用率与统计时间之间关系模型的实证研究

徐鸿飞，杨继民，张 贤

(金陵科技学院 图书馆，江苏 南京 211169)

0 引言

文献利用率是用来统计文献曾经被利用的比率，它间接反映出某文献领域内死书的比率，能较好地衡量图书馆的图书采购质量。经过20世纪90年代的争论，目前普遍采用的计算方式有2种，一种以“种”为计算单位，另一种以“册”为计算单位。目前汇文管理系统提供的利用率统计可分别使用“种”或“册”进行统计[1-2]。

(1)

从该指标的功能来看，笔者倾向于用“种”作为计量单位更为科学，例如某种图书有3个复本，它在统计时间(1年)内被借阅了3次，有可能是每个复本被借阅了1次，也有可能是其中1本被借阅了3次，这2种情况以“种”与以“册”计算的结果差别较大，但实际上并没有多大区别。图书馆统计利用率这一指标的目的是为了检验图书采购与读者需求的一致性，一般认为利用率高则一致性高，利用率低，则一致性低。但使用利用率指标来衡量图书采购的质量有时效性，例如统计10年或20年前入藏图书的利用率，统计结果应该是可信的，但对当前图书采购的指导作用并不大。统计近几年入藏图书的利用率，对图书采购具有重要指导价值，然而，对近几年入藏图书利用率的统计由于时间跨度有限，真实的利用率并不能完全表达出来，其统计结果的客观性与可比性受到质疑。为了正确看待不同统计时间跨度所得到的利用率，有必要弄清利用率与统计时间跨度之间的关系，从而更好地利用这一指标指导与控制图书采购。

1 利用率与统计时间跨度之间的关系分析

为了便于说明问题，可以将图书被读者利用看成是一个概率问题，而影响某种图书被利用概率大小的因素有3个。第1个因素是某种图书在馆内的潜在读者人数。第2个因素是各个潜在读者对该种图书的需求愿望强度，如一个读者对某种书的阅读需求是首选，则需求愿望的强度就大，如果是可读也可不读，或是有时间可以阅读一下，则需求愿望就小。可以假设一下：如果某个读者只借阅一本书时该读者就会借阅某种图书，则该读者对某种图书需求愿望值为1；如果当该读者选择100本书才能选中某种图书，则该读者对某种图书的需求愿望值为0.01。第3个因素是读者的借阅强度，即读者在一定时间内的借阅数量，如有的读者在1年内可能借阅100册图书，有的读者可能只借阅10册图书，则他们的借阅强度分别为100和10。假设某种图书的潜在读者为n，每个潜在读者对该种书的需求愿望值为m，每个潜在读者的借阅强度为t，馆藏图书总种数为z，则某种图书被利用的概率(A)可以用公式(2)表示：

(2)

从公式(2)可以认为当A值越大，该种图书被利用的次数越多，从入藏到首次被利用的时间就越短。图书入藏后首先被利用的图书就是A值较大的图书，随着时间的推移，被剩下没有被利用的图书的A值就越来越小，再被利用的概率也越来越小。再加上读者都有趋新心理，被存放在新书架上的图书与被直接存放到书库内的新书利用率是有差别的，被读者认为是新书，则其被利用的概率要高一些。综合上述的分析，如果以某一年入藏的图书为分析样本，则该年入藏的图书随着时间的推移，被利用的种数应为图1所示的分布。图书在系统中入藏到实际入藏有一个时间差，随着图书的实际分批次入藏，被利用种数约为直线增长，直到图书实际入藏后1～2个月；接着，利用种数的增长逐步减缓，并逐步趋向于理论上的最大利用种数。从上述曲线变化来看，最接近的方程为S曲线[3]，公式为：

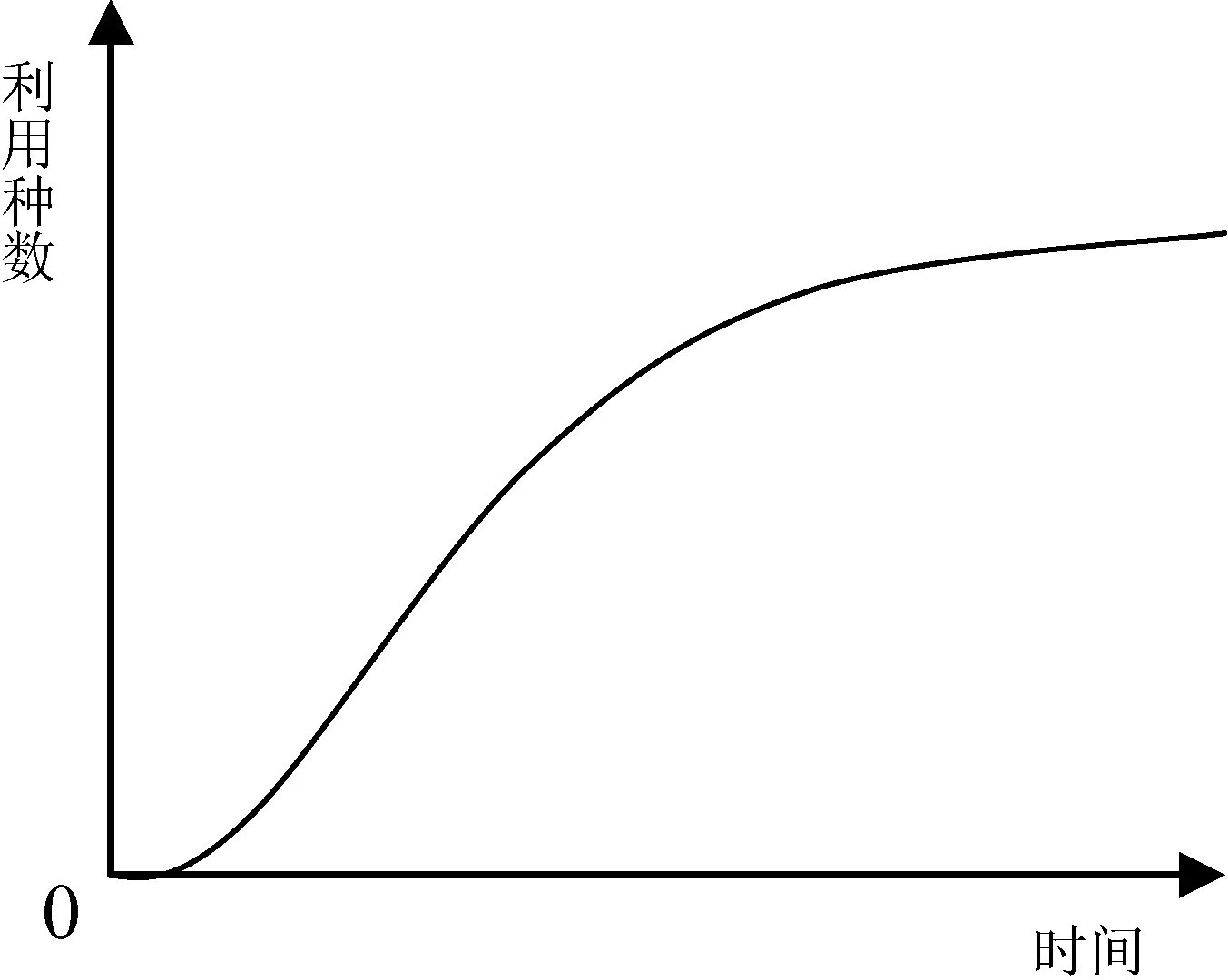
图1 利用种数与时间之间的关系

y=eb+b1/x

(3)

式中，b，b1为回归值。在该公式的两边同时除以样本种数，再乘以100%，则变成入藏后的利用率公式，即图书入藏后，随着时间的推移，也表现为公式(3)的曲线变化，只是系数会发生变化。

2 数据统计与回归

为了论证上述分析，笔者对金陵科技学院图书馆(以下简称“我馆”)图书利用率进行了跟踪统计分析，得出利用率变化最大的时间段是在图书入藏后的3～4年。在此基础上，笔者于2020年5月统计了我馆2017年入藏图书的最早使用时间，统计方法是先从管理系统中提取2017年入藏新的图书记录(不含复本追加)，再利用管理系统统计每种图书的最早被利用时间。按最早利用时间排序，统计各时间段的首次利用种数，时间段划分以年为单位，从开始入藏时间计算，再根据学校流通开放时间，由于每年的2月与8月为寒暑假，将每年1—2月合并为1个月，7—8月合并为1个月，这样每年就分为10个月，每个月为0.1年。再将每个月首次流通种数累加，这样就得到了不同时间点与对应的累积利用种数两组数据。如表1所示，样本总种数为9 898种。

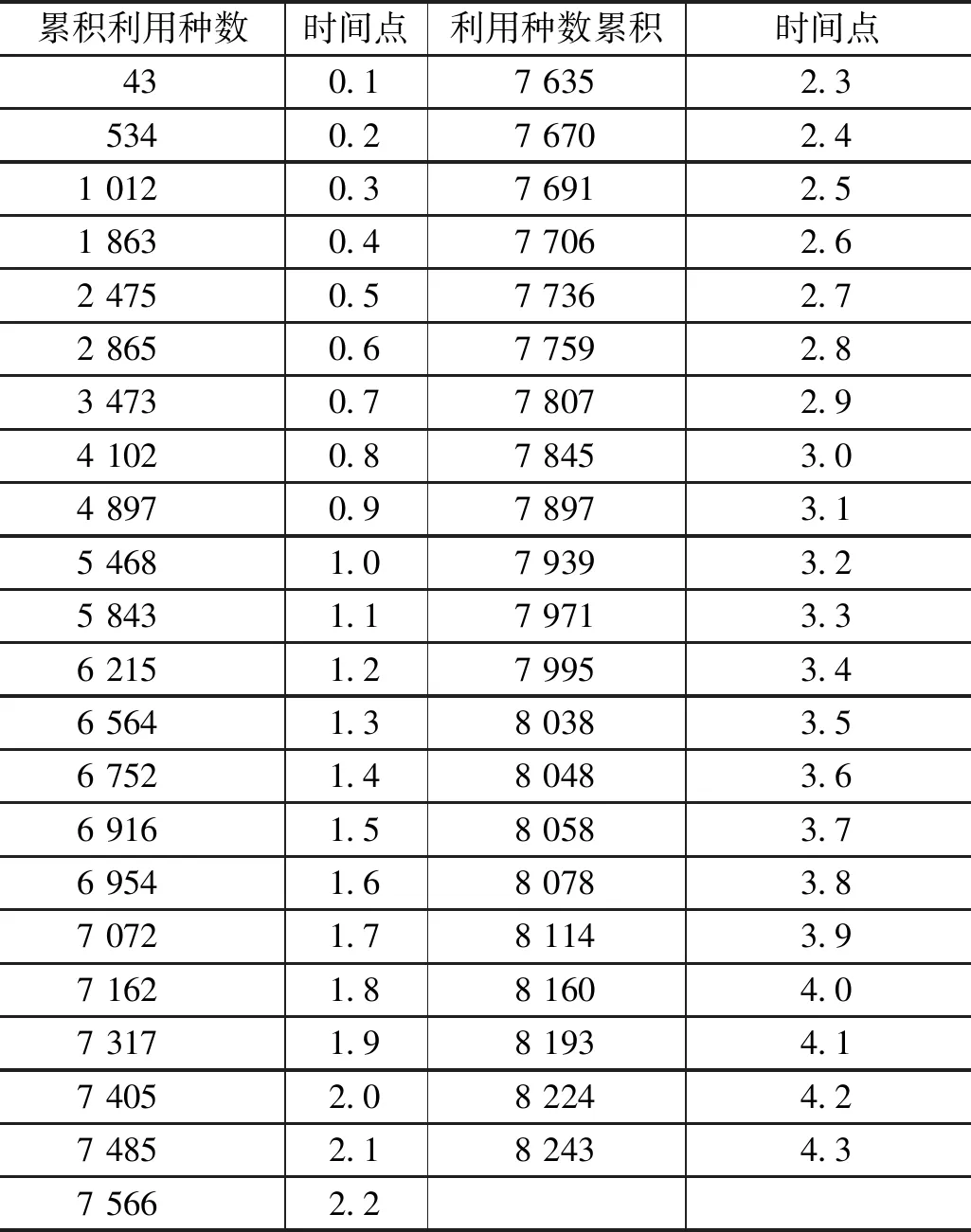
表1 2017年入藏样本统计

根据统计结果，利用SPSS软件回归，得到公式(4)[4]：

y=e9.140-0.563/x

(4)

对于公式(4)：R2=0.988 816 38,F=3 625.077,t1=503.481,t2=-60.209。

曲线拟合如图2所示，统计结果与公式(3)拟合结果良好。

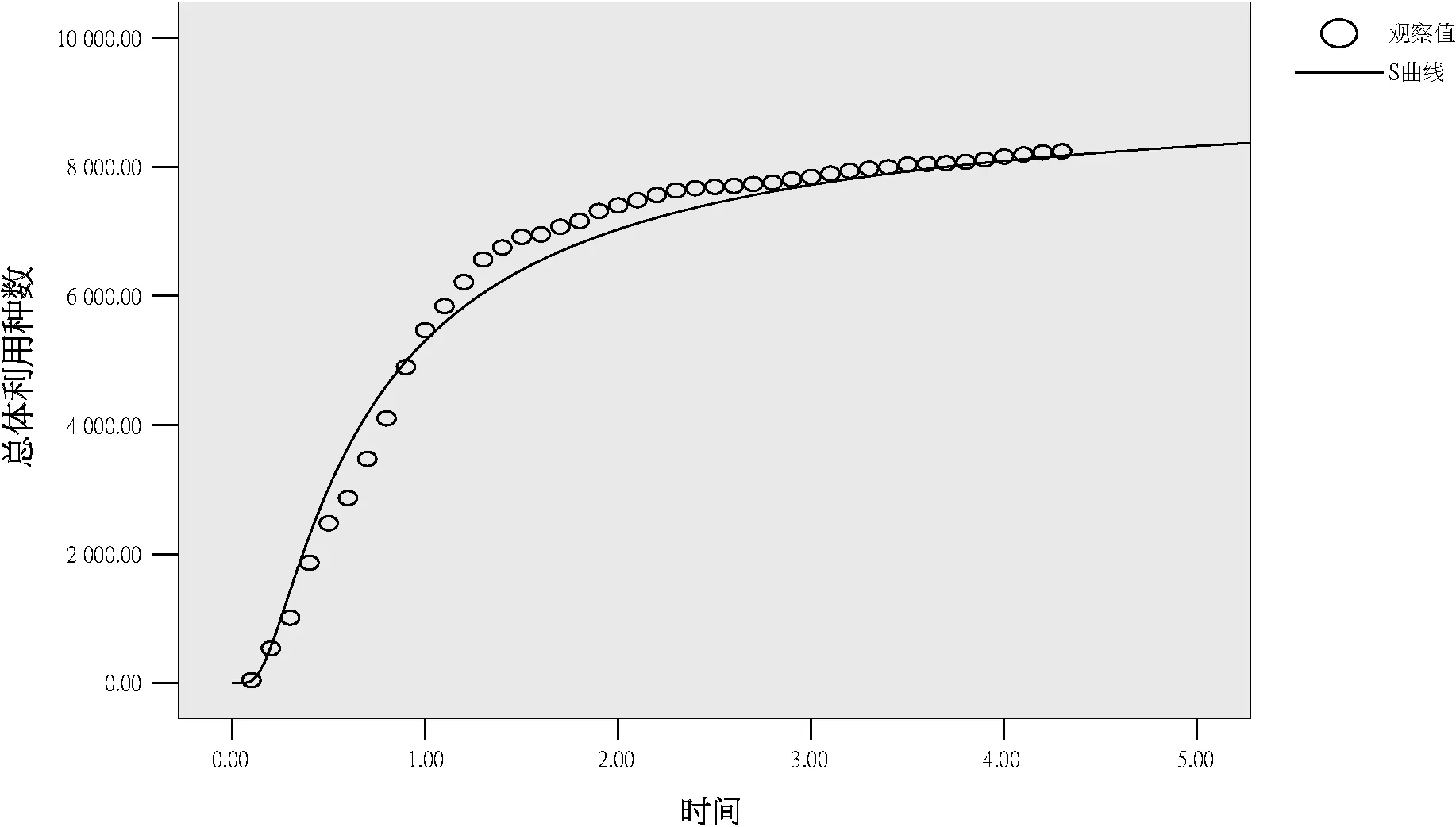
图2 2017年入藏图书利用种数时间拟合

为了进一步证实方程的可靠性，对入藏的8类主要图书(年入藏量大于400种)进行回归分析，回归结果，如表2所示。从回归参数来看，F与t均大于0.01检验水平的临界值，回归效果良好[5]。

在回归的基础上对方程的极值进行了计算，如表2所示。在分析各样本回归曲线时，发现所有曲线存在着一个同样的规律，即在时间点1开始有一段时间的实际值均大于回归值，笔者认为这是因为新书效应对曲线回归所造成的误差；同时，由于各类图书在一年之内不一定能做到均衡入藏，也会造成回归误差。为了排除这两个原因有可能带来的回归误差，保证回归更可靠，采取了放弃时间点在1.3以前的数据，并将利用种数直接换算成利用率进行再次回归，回归结果如表3所示。

表2 2017年8种主要类别与总体样本图书累积利用种数与入藏时间回归情况

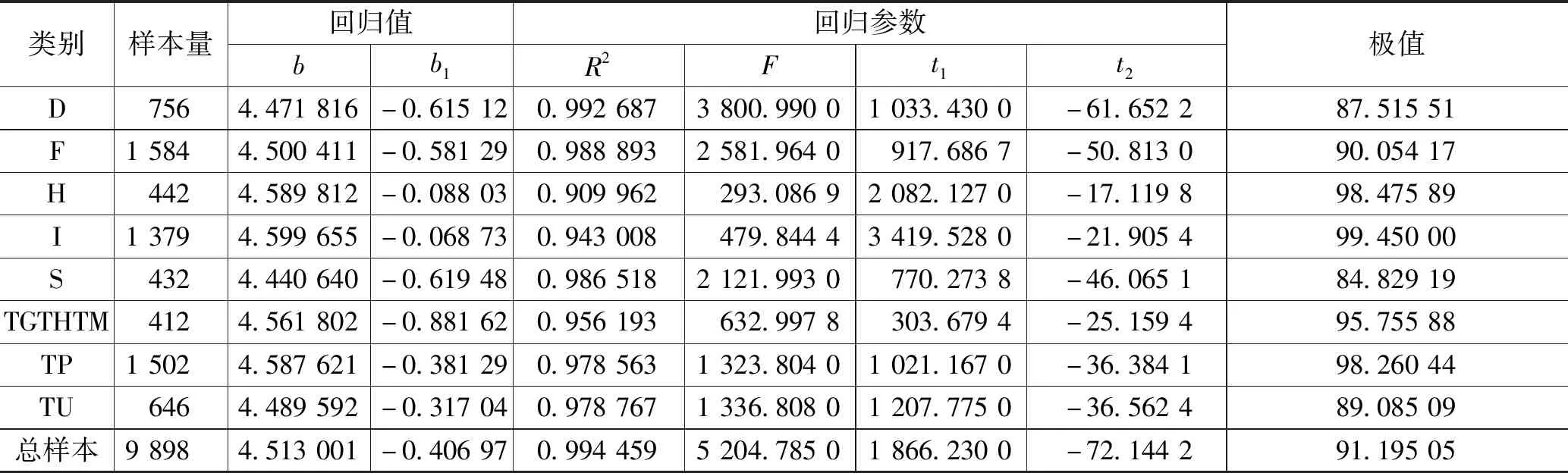
表3 2017年8种主要类别与总体样本入藏后利用率与统计时间回归

从表3的回归结果来看，一年内入藏的图书从下一年的4月开始，其变化规律均服从公式(3)曲线变化。为进一步证实变化规律，以同样的方法统计我馆2018年入藏新书[6]，并对上述8种同样类别图书做了和表3同样的回归，回归结果如表4所示：回归结果同样良好。这充分说明了图书入藏后随着统计时间跨度的变化，利用率遵循公式(3)的变化。

3 曲线变化分析与描述

通过对上述17个样本的统计分析，利用率与图书入藏时间之间的变化如图3所示。当|b1|由大变小时，曲线由图3中第1条曲线向第3条转变，即变化逐步趋缓[7-8]，如I类和H类两类图书的变化和第1条曲线相似，而S类与TGTHTM类变化与第3条曲线相似。出现这种变化的原因有2种解释。第1种解释是，由于不同类别的图书在相同时间内的流通率不同所造成的，第1条曲线代表了高流通率图书，第3条曲线代表了低流通率图书，第1条曲线代表的流通率可能是第3条曲线所代表的流通率的5～10倍，即第1条曲线每种图书1年的平均流通量可能是第3条曲线每种图书5～10年的平均流通量，使得曲线变化缓慢。另一种解释是以图书被利用的概率(A)加以解释，第1条曲线表示在入藏后较短的时间内绝大部分的图书即被读者利用，曲线很快达到较高水平，这说明该类图书中绝大部分图书的被利用概率都比较高。第3条曲线表示入藏后几乎是随机被利用，图书被利用的概率均较低。如以2017年入藏的图书为例，在入藏后的第2年的4月30日，即表3的回归起点时，假设图书的理论入藏(即管理系统的入藏时间) 与图书实际入藏的时间差为半个月，则最后日期(2017年12月31日)至2018年4月30日为2.5个月(2月不计)，若图书馆每个月平均借阅x册次，则2.5个月共计借阅图书为2.5b册次，因此，A>1/2.5x的图书理论上基本上会被读者利用，最早入藏(2017年1月1日)的图书到2018年4月30日的时间跨度为13个月(每年2月与8月不计)，理论入藏与实际入藏借阅时间差为半个月，则实际时间跨度为12.5个月，假设1年中图书入藏基本均衡，即A>1/2.5x的图书应有一半被利用，而A<1/2.5x的图书也有被随机利用的可能。根据上述推断，2018年4月30日没有被利用的图书应基本上为A<1/2.5x。而2017年样本中|b1|最小的I类2018年4月30日时的利用率为94.20%，|b1|最大的TGTHTM类2018年4月30日时的利用率为43.69%，这说明各类图书中A<1/2.5x的比例差别很大，而曲线的变化也主要是这一差别所造成的。当A的平均值越大，A>1/2.5x的比例越高，潜在读者群体越大，流通率越高，|b1|越小，曲线越趋向于图3中的第1条曲线，在较短的时间内趋向饱和值；反之，则A的平均值越小，A>1/2.5x的比例越低，潜在读者群体越小，流通率越低，|b1|越大，趋向于图3中的第3条曲线，达到饱和值的时间也越长。

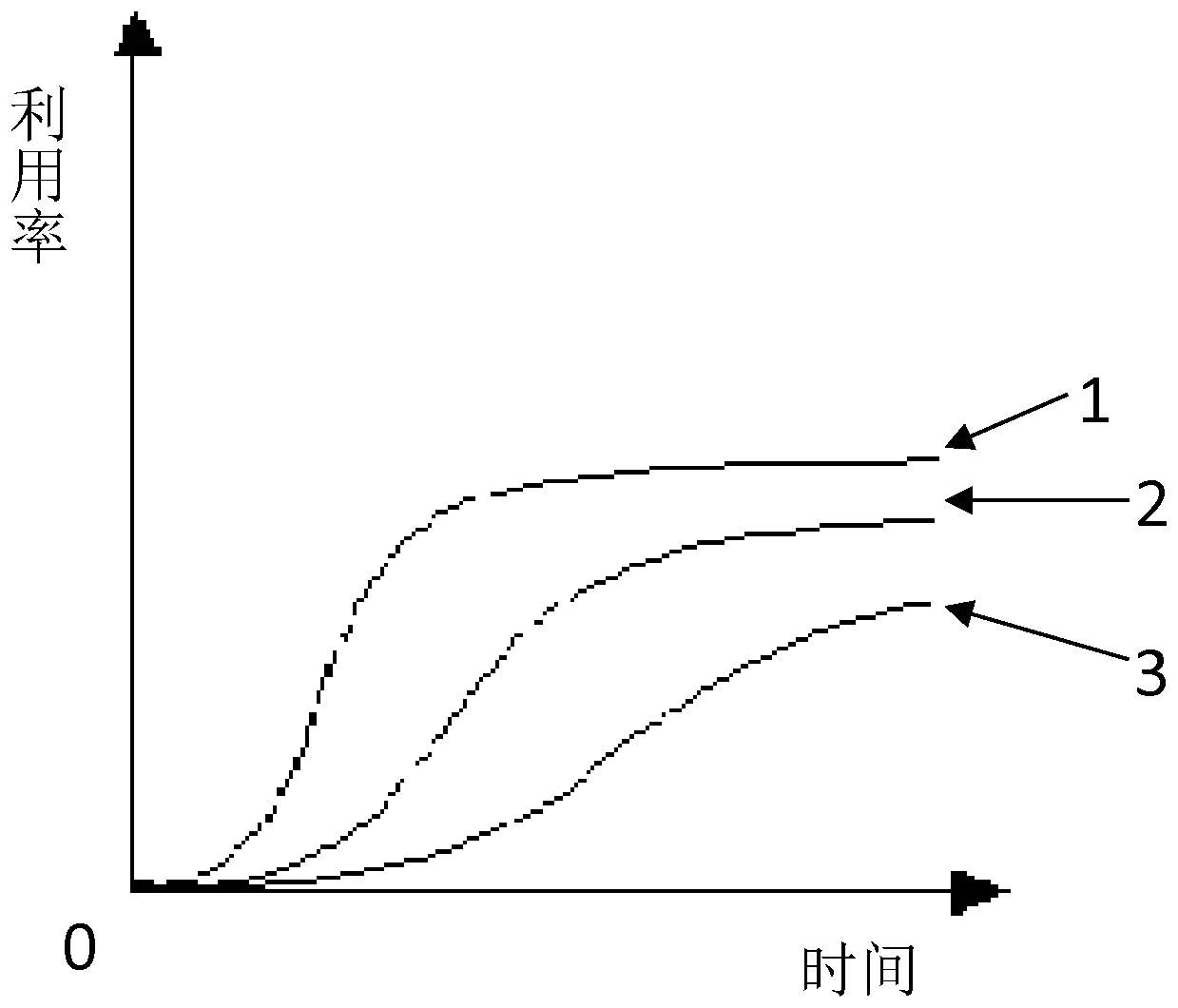
图3 利用率随入藏时间的变化

4 图书采购优劣的判断

每个图书馆各类图书的潜在读者都是客观存在的，图书采访人员如能够根据图书馆各类图书的潜在读者认真选购图书，则图书的最终利用率应该能接近于100%，只是不同类别图书接近饱和值的时间不一样。因此，各类图书对公式(3)回归所得的方程，其yx→∞=eb表达了该类图书采访优劣。当该极值大于100时，则表示该类图书在有限的时间内所有的图书都会被利用；当该极值小于100时，表示该类图书中有一定比例的图书A=0，即在馆内无潜在读者。将表3与表4中8类我馆主要类别图书的统计结果与回归极值进行对比，结果如表5所示：通过该表的比较，各类图书采购的优劣一目了然，如2017年TGTHTM类别yx=1.3时为当年8个类别中的最小值，但其极值达到了近95.76%，说明2017年该类别图书的采购是成功的，同时也说明图书入藏后在较短的时间内统计到的利用率并不能真正反映该类图书采访的优劣。再如2017年与2018年的S类图书利用率的极值均为最低，是8个主要类别图书中采购最差的一个类别，且2017年与2018年相比，采购种数由2017年432种下降到2018年的131种，利用率极值由2017年的84.83%下降到2018年的71.14%，可见2018年该类图书采购的失败。

表5 2年8个类别图书统计与回归极值对照

5 对图书利用率的估计及总体采购优劣的评价

根据上文对不同类别图书利用率变化的规律分析[9]，各类图书变化规律的区别主要是由于从图书入藏到第2年4月期间内利用率高低的区别造成的，从第2年4 月以后，所剩余的图书，其被利用的概率(A)之间的差异相对较小，基本上为A<1/2.5x的图书。假设各类图书被利用概率在1/2.5x>A>0区间分布基本一致，则从时间点1.3以后回归曲线的变化规律应基本一致，即使各类之间有一定的差异(客观上也是有差异的)，但与整个样本之间的差异相比是可忽略的，因此，从时间点1.3以后回归的方程其变化率应基本上是一致的[7]。因此，表示曲线变化率的b1与yx=1.3之间一定存在着函数关系，即b1的大小主要是由yx=1.3的大小决定的。对表3、表4与表5中8种类别16个样本的b1与yx=1.3值通过SPSS软件反复拟合[10]，得出yx=1.3→b1存在对数关系，并对其进行了拟合回归，回归结果见表6。

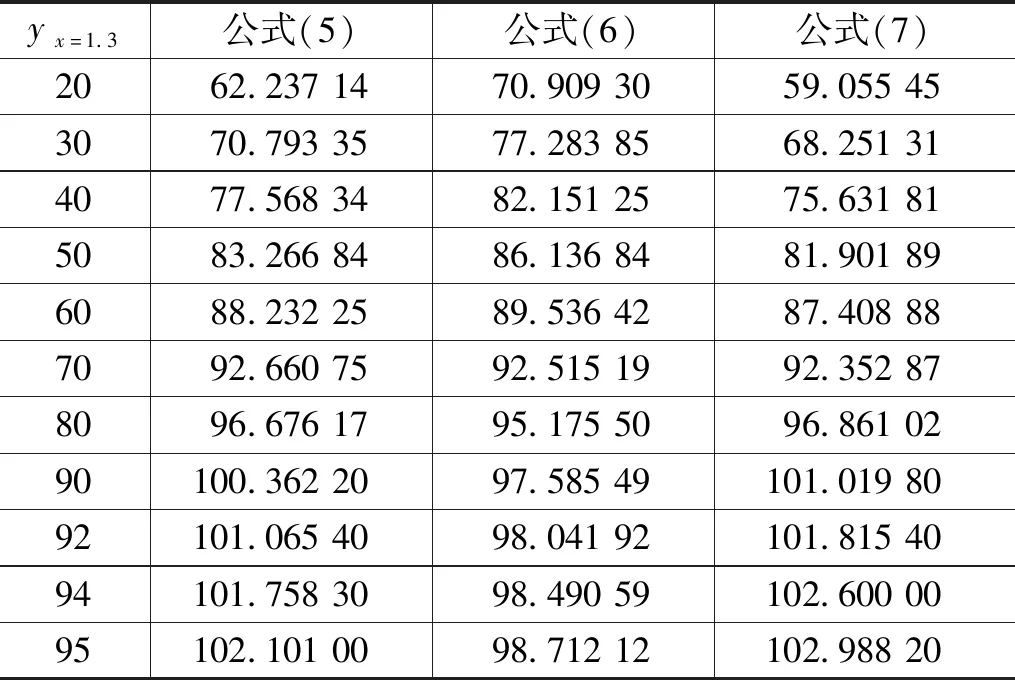
表6 对不同yx=1.3值极值预测

2017年与2018年16个样本总体回归：

b1=-4.133+0.887lnyx=1.3

(5)

对于公式(5)：R2=0.969 491,F=444.882,t1=-23.649,t2=21.092。

在此基础上分别对2017年与2018年8个样本进行回归，回归结果如下：

b1=-4.713+1.024lnyx=1.3

(6)

对于公式(6)：(R2=0.985 790,F=416.224,t1=-22.481,t2=20.402。

b1=-3.912+0.836lnyx=1.3

(7)

R2=0.975 443,F=238.236,t1=-17.483,t2=15.438。

回归结果F与t均大于0.01检验水平的临界值[11]，回归拟合良好，这也进一步证实了上文的判断和分析。由于该方程的回归是忽略了不同类别在回归时间点(1.3)后被利用概率分布的差别，所得到的方程是表达了参与回归类别的总体平均水平，所以回归结果可以表达图书采购优劣的总体水平。根据回归公式(5)(6)(7)对不同的yx=1.3的极值进行计算，结果如表6所示：认为对不同的yx=1.3值预测的极值一致性越好，且越接近100%，则文献采购越优，反之则越差。通过比较，图书馆2017年的图书采购明显好于2018年。如果图书馆的图书采访人员相对稳定，且没有对图书采购做任何调整，则可以用通过yx=1.3→b1的回归所得方程对新入藏图书利用率进行预测[12]。

6 结语

图书利用率是图书馆用来衡量与控制图书采购质量的重要指标，弄清利用率与入藏时间之间的关系，有利于正确使用这一指标指导图书采购。在计算机管理系统下，本文统计分析所需数据系统中均已存在，系统开发人员如能提供直接输出结果的接口，图书馆就能轻松做出上述分析，如果能将该分析作为系统的一个子系统，图书馆就能随时获得各类图书的利用率分析结果，这对优化馆藏、提高图书馆投入产出比具有重要的指导价值。