基于线性扩张状态观测器的PMSM无位置传感器控制

曾香平，赵世伟，尹华杰，肖盼盼

(华南理工大学 电力学院，广州 510640)

0 引 言

永磁同步电机(以下简称PMSM)依靠永磁体励磁，与传统电励磁电机相比，其结构简单、转矩密度大、效率高，广泛应用于要求功率密度高、调速范围广的场景。PMSM调速系统需要反馈速度与位置信号[1]，采用物理传感器如位置霍尔传感器或编码器将增加电机的体积和成本，降低系统的运行可靠性[2]。

有学者提出从定子侧易测物理量(电压、电流)中提取与转速、位置相关的量，从而实现无位置传感器控制[3]。根据适用速度范围不同，PMSM无位置传感器控制策略可分为两类：零低速时，利用电机凸极特性设计无位置传感器控制，例如高频注入法[4]；中高速时，利用观测器观测反电动势或者磁链，再结合正切计算法或锁相环(以下简称PLL)估计电机转速和转子位置，实现无位置传感器控制[5-6]。

无位置传感器控制中常用的观测器有滑模观测器[7]、模型参考自适应观测器[8]、扩展卡尔曼滤波器观测器[9]等。传统滑模观测器适应性强，对参数变化鲁棒性较好，但其变结构控制方式引入了抖振。模型参考自适应观测器观测精度高，但对电机模型依赖强，抗扰动能力差。扩展卡尔曼滤波器有较强的抗扰性，但需要通过大量复杂的矩阵运算才能实现观测，对硬件的计算能力要求高。

扩张状态观测器(以下简称ESO)是自抗扰控制器中核心环节。文献[10]提出构造两个非线性ESO，利用电机电压方程和机械方程，分别观测电机反电动势和转速。基于ESO的无位置传感器控制观测精度高、抗扰动能力强，相比于非线性观测器，线性扩张状态观测器(以下简称LESO)调参更方便，且可以实现频域分析[11-12]。

本文提出利用LESO观测反电动势。LESO为线性模型，易于进行理论分析，可以通过频域法推导观测反电动势与实际反电动势之间的传递函数，获得观测反电动势相位滞后角的数学计算公式。为了提取反电动势观中的速度、位置信息，本文利用三角函数构造位置差频信号，通过PLL准确提取反电动势信号中的转速、位置信号。相比于传统正切计算法，PLL能够抑制观测反电动势误差带来的噪声。最后通过MATLAB仿真和实验验证该方案能够准确获得电机转速和转子位置信号，实现无位置传感器转速控制。

1 表贴式PMSM的数学模型

表贴式PMSM气隙磁场均匀，交轴电感和直轴电感差异很小，电机可视为隐极。假设电机三相定子绕组对称，电机旋转时定子侧感应反电动势波形为标准正弦波，忽略铁心饱和，则表贴式PMSM在静止α，β轴坐标系中的定子电压方程：

(1)

式中：uα，uβ，iα，iβ，eα，eβ分别为α，β坐标系下电压、电流以及反电动势；R为定子相电阻；L为定子相电感。

电机旋转，永磁体感应出的反电动势：

(2)

式中：ψf为永磁体磁链；ω为电机电角速度；θ为转子N极与a相轴线的夹角。

2 基于LESO的反电动势观测

2.1 LESO设计

由式(1)可见，α，β坐标系下两个电压方程相互解耦，且两个电压方程除下标外完全一致，以下仅以α轴电压方程为例进行陈述。将反电动势视为未知量，引入“扩张状态”：

(3)

反电动势可微分求导数，设：

(4)

可以将式(1)中α轴电压方程写成状态空间方程：

(5)

定义观测误差：

(6)

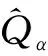
(7)

可构造LESO：

(8)

式中：β1α、β2α为观测器参数。

2.2 LESO收敛性证明

将式(8)的观测器与原系统扩张状态式(5)作差，得到：

(9)

改写成矩阵形式如下：

(10)

观测器参数可配置如下：

(11)

式中：ω0>0。对式(10)进行拉氏变换：

(12)

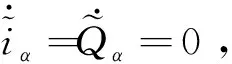
(13)

因此，可以增大ω0，使得LESO观测精度满足要求，实现系统状态观测。

2.3 ESO观测反电动势分析

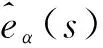
(14)

即:

(15)

根据式(15)，绘制Bode图如图1所示。

图1 反电动势观测值与实际值传递函数Bode图

从幅频特性可以看出，观测器具有低通特性，而且随着ω0的提高，幅频特性会往右移动，从而导致带宽增加，其高频增益也相应提高。因此ω0可以表征观测器的带宽。从相频特性可以看出，随着频率提高相位滞后角度会随之加大，但是随着ω0的提高，相同频率下的相位滞后会相应减小。

对于该观测器来说，带宽过小，相位滞后会比较明显；带宽过大，容易引入高频干扰，所以需要依据系统实际需求选择恰当的带宽。

3 基于PLL的位置观测

3.1 PLL设计

设计PLL提取反电动势观测值中的速度位置信号。PLL的结构如图2所示。

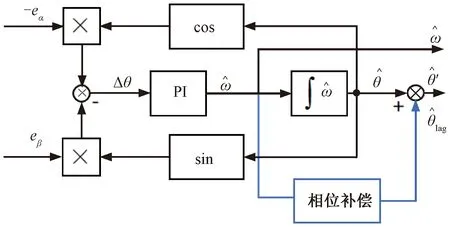
图2 PLL结构图

由式(2)和图2可以得到：

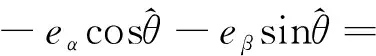
(16)

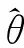
(17)

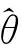
(18)

式中：kp和ki为PI环节系数。合理配置kp和ki，可以利用式(18)的低通特性获得平滑且准确的位置估算信息。

3.2 相位补偿

根据频域法，式(15)可写作：

(19)

可见，传递函数式(19)的相频特性：

(20)

即观测反电动势相位滞后：

(21)

最终观测位置：

(22)

4 仿真与实验

4.1 仿真分析

为了验证该策略的可行性，利用MATLAB搭建如图3所示的仿真模型，电机参数设置如表1所示。

图3 仿真实验原理框图

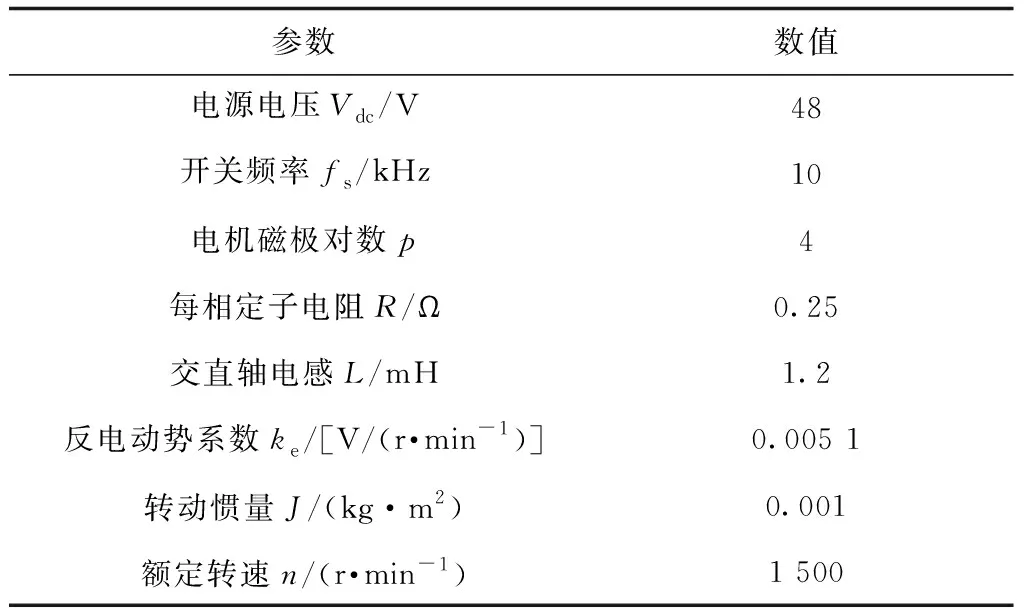
表1 仿真电机参数模型

在仿真过程中，最初的参考转速设置为750 r/min，在1 s时参考转速改为1 500 r/min。结合仿真需求，电机运行的最高转速不超过1 500 r/min，即反电动势的频率不高于100 Hz，设置LESO参数ω0=5 000。由图1可见，此时LESO的截止频率511 Hz。100 Hz的反电动势信号通过LESO幅值损失几乎为0，相位滞后约为14°，需要做相位补偿。并设置PLL中的参数Kkp=5 000；Kki=800。

首先验证LESO能够精确观测反电动势。系统速度和位置反馈均由电机输出实际值提供。观测器只做观测，其输出观测值不参与闭环。图4为LESO观测的反电动势稳态值。

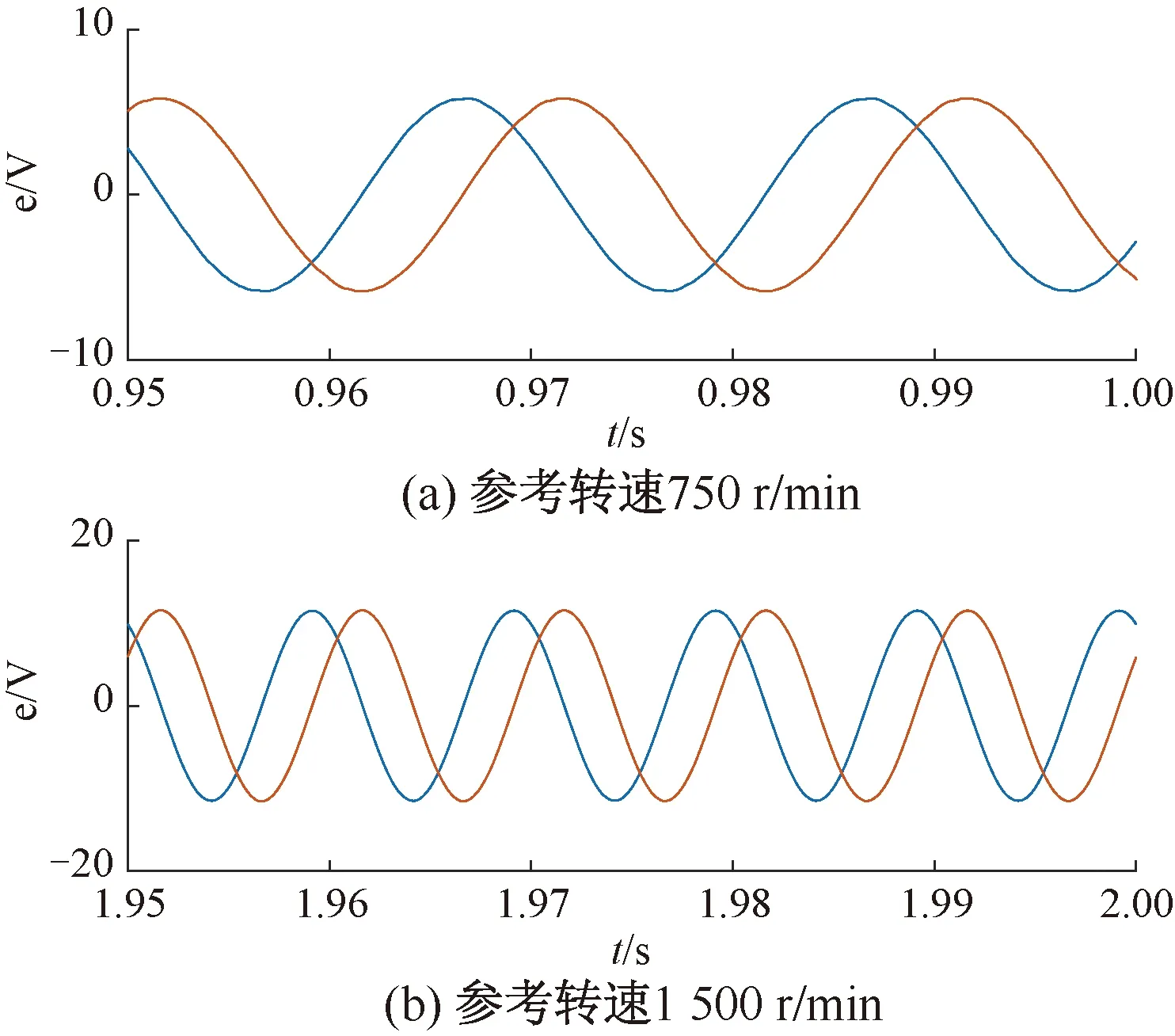
图4 观测反电动势结果比较

由图4波形可以看出，LESO观测的反电动势正弦度高，谐波含量小。对观测反电势稳态值进行傅里叶分解，转速为750 r/min时，谐波畸变率为1.4%；转速为1 500 r/min时，谐波畸变率为0.7%。这是因为低速时，电机反电动势幅值较小、信噪比较低。

观测反电动势经过PLL获得的位置信号如图5所示，位置观测误差如图6所示。

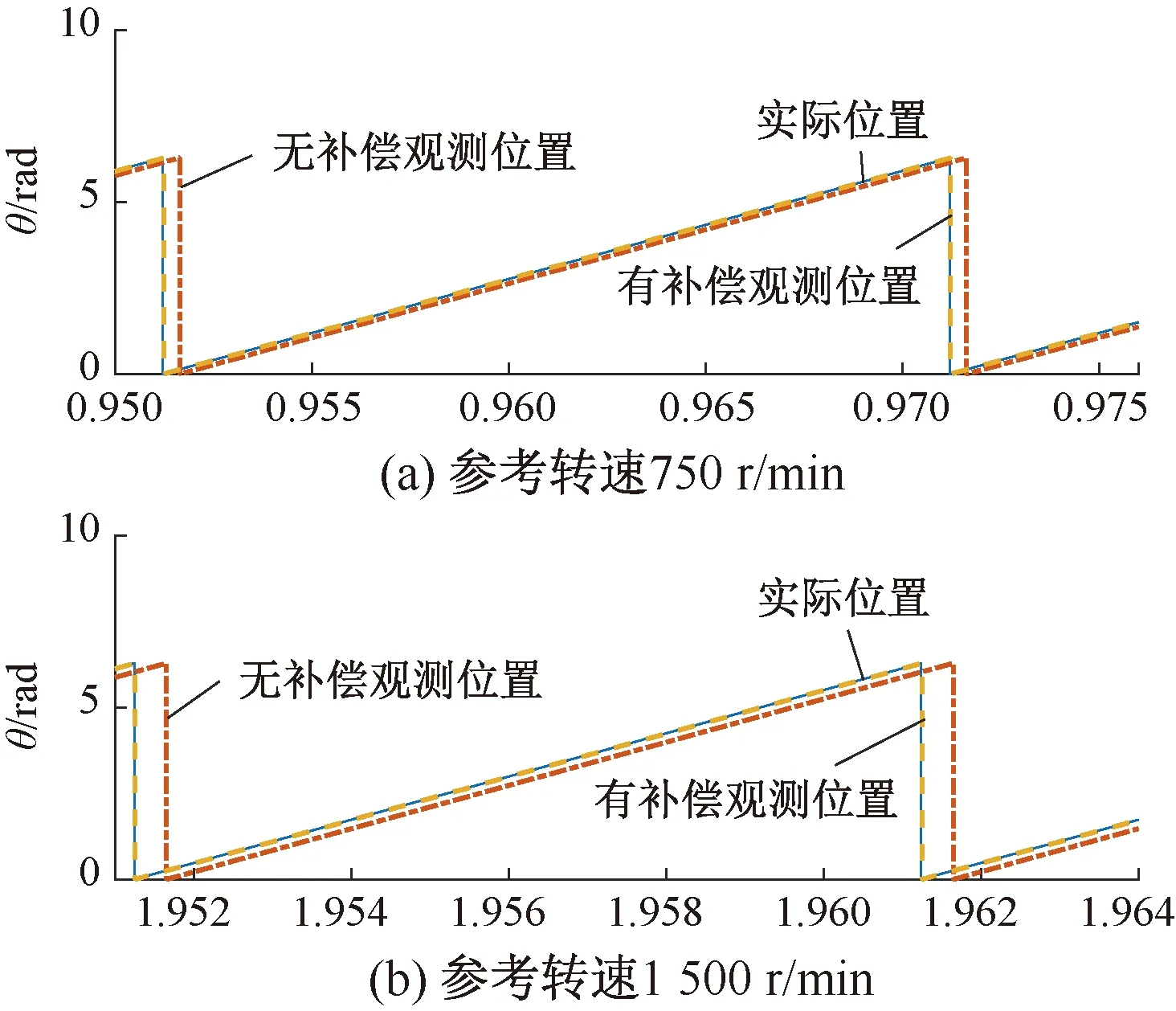
图5 位置观测结果比较

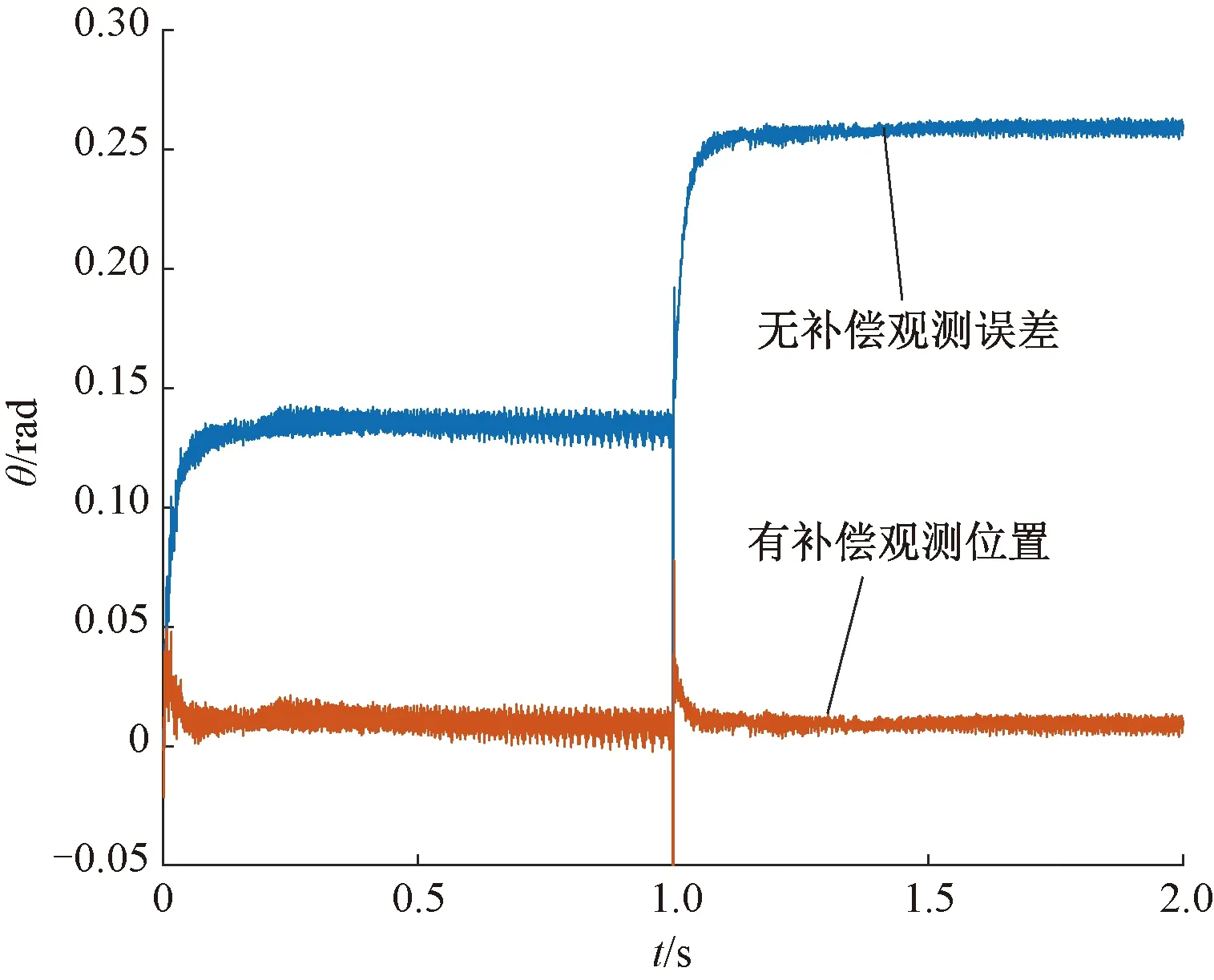
图6 观测位置误差比较

当位置设有相位补偿时，电机转速为750 r/min，观测位置误差为6°；转速为1 500 r/min，观测位置误差为15°。位置角度补偿后，两种转速下的相位滞后皆为0.5°。可见，利用式(19)可以有效补偿相位滞后，提高控制策略适用速度范围。

速度观测值如图7所示。

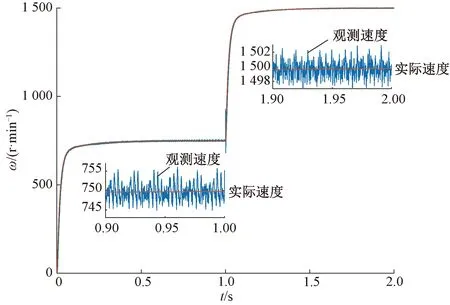
图7 观测器开环速度观测结果比较

可见，稳态时转速估计精度高。在750 r/min时，速度观测值波动范围约为(750±2) r/min；转速为1 500 r/min时，速度观测值的波动范围约为(1 500±5) r/min，相比于低速，高速时速度观测值更平滑。

将观测器投入系统，闭环系统的速度响应如图8所示。

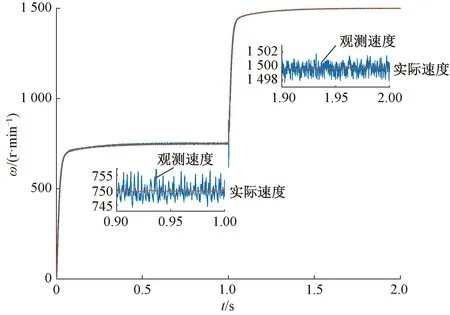
图8 观测器闭环速度观测结果比较

观测速度存在一定程度的波动，但经过系统惯性环节，实际速度响应曲线平滑。利用该控制策略可以实现无位置传感器速度控制。

4.2 实验分析

实验平台如图9所示，实验电机与仿真模型中的电机参数一致，控制器驱动板主控芯片为STM32F103RCT6，驱动电路三相全桥逆变器开关频率为10 kHz，通过串口总线与PC上位机相联接，传输观测器观测的位置信号和速度信号，以及编码器输出的位置信号和速度信号。

图9 实验平台

设置参考转速750 r/min，在3 s时，参考转速突变为1 500 r/min。当观测器观测速度平均值与编码器观测速度平均值误差小于6 r/min时，从有传感器控制系统切换为无位置传感控制系统。LESO+PLL观测的位置信号和编码器观测的位置信号对比如图10所示，LESO+PLL观测的转速曲线和编码器观测的转速对比如图11所示。

图10 实际位置与观测位置比较

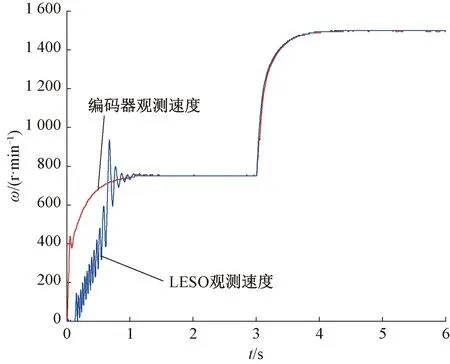
图11 实际速度与观测速度比较

从图10可以看出，不同转速下的观测位置与实际转子位置重合，观测效果较好。由图11可以看出，速度观测平均值都能收敛到实际转速。

5 结 语

本文利用LESO观测表贴式PMSM反电动势，证明了观测器的收敛性，且利用观测反电动势与实际反电动势之间的传递函数，讨论了LESO相关参数的设置方法，推导了补偿角的计算公式。在此基础上，本文采用PLL估计了电机转速和转子位置。

本文搭建了无传感器的仿真模型与实验平台，对位置估计和无传感器速度控制进行了仿真和实验对比分析。仿真和实验结果均能实现准确的转子位置估计，与理论分析较为吻合，验证了本文所提出的LESO+PLL位置估计算法和无传感器速度控制方案的有效性。