融入社会心理学理论的教与学优化算法

何佩苑，刘 勇

上海理工大学 管理学院，上海 200093

教与学优化算法（teaching-learning-based optimization，TLBO）是Rao 等人于2011 年提出的一种新型启发式算法。该算法模拟教师和学生的教与学过程设计，学生不仅可以从教师的授课中获得知识，还可以通过学生间的互动获得知识。TLBO 算法具有参数少、结构简单、求解速度快等优点，其竞争力主要来源于对教阶段与学阶段的巧妙设计。与其他典型改进智能优化方法相比，TLBO 算法也展现了其突出的性能与优势。例如，与遗传算法（genetic algorithm，GA）相比，TLBO 在教阶段让种群向最优个体学习，从而提高了算法的收敛速度；与微粒群算法（particle swarm optimization，PSO）相比，对于单个算子，TLBO 比PSO 多引入了一个学阶段，有利于提高算法的勘探能力；与布谷鸟搜索算法（cuckoo search，CS）相比，TLBO 在学阶段提供了交互式学习的方法，减少了算法陷入局部最优的概率。正是因为TLBO 具有这些优点，自算法提出至今，学者们对它的研究从未停止。然而TLBO 算法本身也存在寻优精度低、稳定性差、收敛速度较慢等不足，许多学者从多个角度对其进行了改进。改进方向主要分为改进教学过程、引入权重或适应因子和与其他智能优化算法相结合三方面。其中，对于教学过程的改进是指在原始教阶段与学阶段的基础上，加入自学的阶段或引入新的学习规则，例如：Dong 等人提出了一种改进学阶段和新颖的自学习阶段的协作学习模型（collaborative learning model，CLM）。在CLM 方法中，为了有效地引导学习者，在自学阶段，老师会根据邻域信息自适应地更新其位置。Ge 等人提出了一种新颖的基于自主学习的优化算法，根据教学过程的三个阶段，老师的学习、学生之间的相互学习和自我学习，对提出的算法进行了重新建模。Zhang 等人引入了具有对数螺旋策略和三角形突变规则的教与学算法来增强学阶段的探索和开发能力。何杰光等人提出了一种基于多反向学习的教与学优化算法，建立混合反向学习模型，同时增加了基于搜索边界指导的自学习阶段，使得算法具有更强的全局搜索和局部探测能力。Li 等人采用了额外的反馈学习阶段来进一步加快收敛速度，记录上一代教师并与当前教师进行交流，以向学习者提供综合反馈并监督学习方向，以避免浪费上一代的计算量。李丽荣等人在算法后期让教师个体执行动态随机搜索算法，来提高最优个体勘探新解的能力。对于引入权重或新的参数方面的改进，Verma 等人提出基于高级教学-学习的优化算法，在该算法中引入了新的权重参数，以提高准确性和加快收敛速度。Wu等人提出了非线性惯性加权基于教学的优化算法。该算法将非线性惯性加权因子引入基本的TLBO 中以控制学习者的记忆率，并在教阶段和学阶段使用动态惯性加权因子来代替原始随机数。吴聪聪等人在“教”阶段和“学”阶段引入差分算法的交叉算子，同时在精英个体周围按正态分布进行自适应局部搜索，提高算法的收敛速度和求解精度。许多学者为了提高TLBO 的性能尝试将其与其他优化算法融合：Zhai 等人在TLBO 中增加了纠错策略和柯西分布，其中柯西分布用于扩展搜索空间和纠错以避免弯路，从而获得更准确的解决方案。黎延海等人将和声搜索与教与学优化算法相结合，提出了一种基于和声搜索和教与学优化的混合优化算法，使算法能够求解更多的较为复杂的优化问题。李丽荣等人提出了一种融合头脑风暴思想的改进教与学优化算法并在算子中引入柯西变异和一个与迭代次数关联的随机参数，以提高算法性能。Tuo 等人提出了一种混合和声搜索算法改进的TLBO，其中，和声算法部分主要探索未知区域，而TLBO 则旨在快速开发已知区域中的高精度解决方案。

TLBO 作为一个以人为活动主体，模拟教学现象的新型启发式算法，学者对其的改进主要集中在模拟教学过程和与其他算法结合上。然而对于人的心理情感因素考虑得却很少，例如从人的角度出发考虑心理因素对行为结果的影响；不同性格的个体在相同环境中所呈现出的状态不同等。这样改进使得算法在寻优性能上有一定提高，但稳定性和收敛速度方面仍有上升空间。

为了进一步提高算法的性能，本文聚焦社会心理学，考虑人的情感与行为，模拟教学过程中人的心理因素对结果产生的影响。将社会心理学理论应用于算法改进之中。在教阶段中加入“期望效应”理论。该理论指在人际互动过程中，一方对另一方有期待，那么怀有期待的一方便会按照他所期待的那样对待另一方，从而引起另一方行为上的改变。在算法中的体现为教师个体对适应度值好的学生进行一对一教学，被一对一教学的学生受到教师的辅导，也改变自己的学习行为，开始向其他同学学习。在学阶段中加入“场独立-场依存”理论。该理论根据人对外部环境的不同依赖程度把人们的认知方式分为“场独立型”和“场依存型”两种。从现实情况出发，考虑到不同学生的认知风格不同，模拟了场独立型和场依存型的学生，对其采用不同的学习策略。学生在经过教师教学和同学互学后，需要对知识点进行消化，对自身的排名进行评估。根据排名情况延用或及时调整学习方法，因此在学阶段之后加入自我学习方法调整阶段。心理学中存在班杜拉“自我调节理论”，该理论表明自我调节包括自我观察、自我判断、自我反应三个过程。根据此理论成绩对处于不同位置的学生采用不同的自我调节策略，以求达到更好的状态。最后使用一系列测试函数证明改进算法无论在寻优精度还是收敛速度方面，均获得了较优的表现。

在算法改进中加入社会心理学，对于智能优化算法改进领域也具有一定的创新。由于人是一个复杂的系统，受到心理状态的影响，会及时采取措施调整行为来寻求自我保护感。因此，与其他智能优化算法的改进方式相比，融入人的心理因素可以使得算法改进更加灵活，更好平衡算法全局和局部搜索。

1 教与学优化算法

TLBO 是Rao 等人模拟班级教学过程中的教师教学和学生学习两个阶段设计出来的算法。它将整个种群充当班级，种群中最优秀的个体充当老师，其他个体充当学生。算法分为“教阶段”和“学阶段”。“教阶段”意味着班集体向老师学习；“学阶段”意味着同学之间相互学习。通过这两个阶段的协同进化，从而提升种群的整体水平。本文将总的学生数量（即种群大小）记为，每个学生所学科目的数量（即个体的维度）记为。每个学生记为X={x,x,…,x}，用适应度函数(X)表示学生的成绩，适应度值越好，表明该学生成绩越优秀。算法具体内容表述如下。

1.1 教阶段

在教阶段，每次迭代中适应度值最好的个体将被选为教师，教师向学生传授知识来提高全班的平均成绩，他希望班级整体的平均位置向自身靠近。因此教学方式设计由式（1）给出：

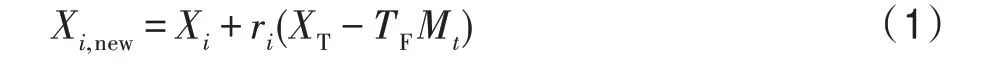
其中，X表示学生经过教阶段学习之后的新状态；X为学生学习前原始状态；r为[0,1]上的随机数；为教学因子，反映教师对于班级平均值的影响程度，一般取1 或2。

教阶段完成后，学员更新知识储备，每个学员根据新状态和原始状态的成绩来决定是否要更新。以最小化问题为例：

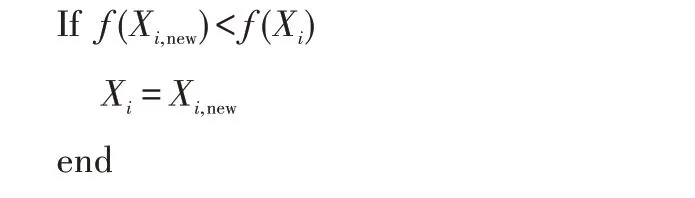
1.2 学阶段

这个阶段模拟的是课堂结束后，学生之间相互学习的过程。学生为了进一步提高自身的学习水平，与班级中的其他个体进一步交流。学生随机选择学生，比较两个学生的适应度值，用优秀学生的位置减去次优者。以最小值优化问题为例，采取如下方式进行学习：

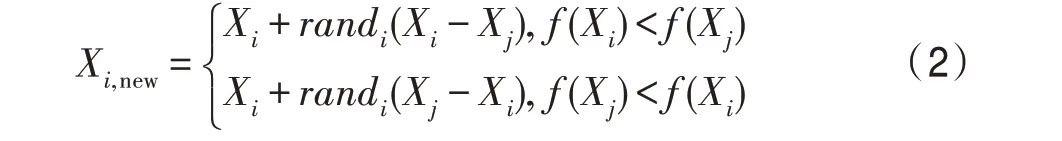
其中，rand为[0,1]上的随机数。

学阶段结束后对学生再次执行与教阶段相同的更新操作。

2 基于社会心理学理论的教与学算法

为了进一步提高算法的性能，本文从人的情感心理角度出发，结合社会心理学理论对教与学算法的三方面进行了改进。首先在教阶段引入“期望效应”理论，承受不同程度期望的学生将采取不同的学习策略。在学阶段引入“场独立-场依存”理论，将不同类型的学生学习方式的差异区分开来。考虑到现实教学情况，在教阶段与学阶段之后加入自我学习方法调整阶段，用于及时调整学生的学习方法。

2.1 引入“期望效应”理论改进“教阶段”

在日常教学中，教师总是会对成绩相对优秀的学生有更高的期望。为了使其获得更好的成绩，教师会采取一对一教学或开设提优课等方式。成绩较好的学生受到教师的重点关注后，为了不辜负老师的期望，会采取积极的措施更加刻苦地学习。例如采取增加学习时间、多与同学交流学习经验等方式来提升自己。这一现象在社会心理学中被称为“皮格马利翁效应”，即“期望效应”。期望是对自己或他人的一种判断，希望自己或他人达到某种目标或满足某种行为预期。由期望而产生的行为结果就是期望效应。期望强调的是个体心理激发的活动过程，而期望效应则侧重因为心理激发而产生的行为结果。哈佛大学教授J.Sterling Uvillgston 将该理论引入企业管理实践之中，结果表明：管理人员对下属的期望以及对待下属的方式在很大程度上确定了这些下属的工作绩效和职业进步。受此启发，对算法做出如下改进：将成绩在班级平均分以上的学生归为优秀学生，对其采取教师一对一教学和向其他同学学习经验相结合的方法进行学习，如式（3）所示：

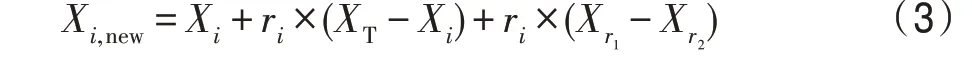
对于成绩在班级平均分以下的同学，将按照式（4）进行学习：

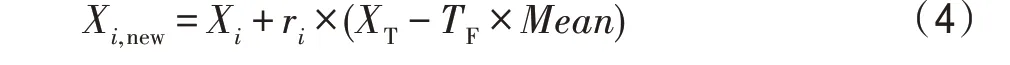
其中，X与X分别为班级里任意两名同学的状态，为班级同学的平均水平。当学生的适应度值高于平均值时，将承受教师的高期望。由式（3）可以看出，学生为了满足教师的期望，在学习过程中除了依赖自身知识状态X，还采取了向教师一对一学习r×(-X)和向同学学习r×(X-X)的措施。对比式（1），学生在学习中参考了教师与班级平均的差值，在这种学习方式下，优秀学生提高成绩的空间有限，会降低算法向最优解收敛的速度。在改进式（3）中加入向教师一对一学习的策略，增加了教师对于学生的影响，这样设计不仅可以让优秀学生快速向教师靠近，还可以使学生跳出自身状态带来的局限性，解决算法局部搜索能力差的问题。此外，为了加快算法的收敛性，式（3）中加入了向同学学习的策略。平均分以上的学生与班级中任意同学交流经验，在提升自身的同时，也有助于他人成绩的提升，从而缩小班级差距，加快整个种群向最优值收敛的进程。当学生适应度值低于平均值时，他不承受教师的高期望，因此他的学习方式不会发生改变。

2.2 引入“场独立-场依存”理论改进“学阶段”

在标准的教与学算法的学阶段中，学生个体采取统一方式进行学习。然而在现实情况中，不同性格的学生采取的学习方式不同。有的学生性格内向，较为独立，倾向于在独自学习的过程中积累经验；有的学生性格外向，善于社交，喜欢在与人探讨交流问题的过程中收获知识。这两类学生在社会心理学中分别被称为“场独立”与“场依存”类型学生。场独立性与场依存性这两个概念来源于威特金（Witkin）对知觉的研究。场独立性者对客观事物作判断时，倾向于参照自身，不易受外来因素影响和干扰；场依存性者倾向于参照外部对信息进行加工，独立性较差且容易受外界的影响。在学习活动中，由于认知风格的差异，场独立型和场依存型的学生倾向于不同的学习策略。场独立型学生的知识来源主要由自身知识积累和与极少数同学讨论这两方面组成；场依存型学生的知识主要来源于部分自身知识和广泛社交讨论。在算法设计方面，考虑到不同学生在学阶段受外界影响程度不同，随机生成0-1 矩阵()，模拟场独立型（为1）和场依存型（为0）的学生，对其采取不同的学习策略：场独立型学生采取式（2）的学习策略进行学习；场依存型的同学按照如下策略进行学习：

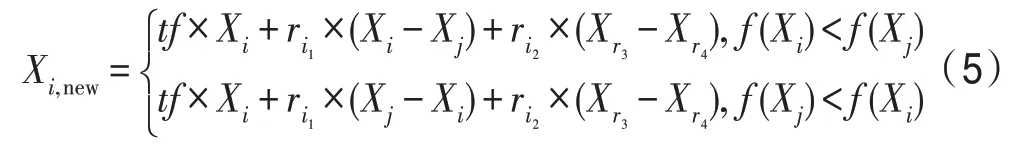
由式（5）可知，X、X、X为随机选中的三名学生，r与r为[0,1]上的随机数，为比例因子，用于降低对上一时刻自身状态的保留率。经过多次得出将值设为0.3 时，算法的运行结果最好。当()为1 时，代表学生个体X为场独立性，在学阶段按照原始算法的学习方式进行学习，对上一时刻自身状态完全保留。当()为0 时，代表学生个体X为场依存性，在学阶段除了随机挑选一名学生学习以外，还会与其他同学交流经验，并吸收部分他人知识用于提高自身成绩。此时，学生X仅保留部分自身状态。与原始算法中学阶段相比，这样设计削弱了上一时刻状态的影响力，同时增强了个体间的交流，降低了算法陷入局部最优的概率，并且维持了解的多样性。由于另一半粒子完全保留自身状态，算法的收敛速度也得到了保障。

为验证改进学阶段对学生多样性的影响，在学阶段设置程序断点，运行结果如图1 所示。

图1 学生的多样性对比图Fig.1 Comparison chart of students'diversity

选取部分测试函数，在算法迭代30 次时绘制学生位置图，将改进算法与原始TLBO 进行对比，可以发现学生的多样性得到了大幅提升。

2.3 加入自我学习方法调节阶段

学生在经过教师教学和与学生交流两个阶段的学习后，需要对自身的学习情况有一个精准的认识。因此自我评估与调节在高效学习中扮演者不可或缺的角色。班杜拉在社会学习理论中提出了自我调节理论，强调的是个人的内在强化过程。自我调节包括自我观察、自我判断和自我反应三个基本过程。人们根据社会活动的标准对自我行为进行观察，并判断自我行为与标准之间的差距对自我做出肯定或否定的评价。依据自我评价，个体会产生各种内心体验，如自我满足、自怨和批评等，这是自我调节的最终结果。人们可以利用自我调节结果，采取更加适宜的策略以达到目的。基于此理论，本文在教阶段和学阶段之后加入自我学习方法调节阶段，为学生提供一个自我反省并及时调整学习策略的平台。自我学习方法调节阶段具体设置如下：经过教阶段和学阶段之后，计算整体学生的平均分，将成绩高于平均分的个体归为优秀个体，并计算优秀学生的平均分。根据整体平均分和优秀学生平均分将班级同学分为三大类：

当学生成绩高于优秀学生的平均分时，该学生为优等生，证明其学习方法是高效的，因此学生将沿用自己的学习方法继续学习，如式（6）所示：

当学生成绩低于优秀学生平均分，但高于班级整体平均分时，该生为普通生，证明其学习方法部分有效，但仍有改进空间，可以微调学习方法以获得更好的成绩，如式（7）所示：

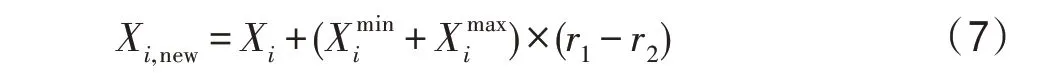
当学生的成绩低于班级平均分时，证明自身学习方法没有效果，需要很大程度地改变学习策略，此处用反向学习的方法，如式（8）所示：

另外，由于TLBO 算法思想源于模拟班级的教学过程，为更好模拟教阶段中学生的新状态，引入自适应学生更新因子，以期待算法获得更好的效果。

2.4 自适应学生更新因子

在教师“教”的过程中，新状态学生的知识储备是由自身原有知识与向教师学习所积累的知识两部分组成。在学习初期，学生由于对环境和知识点存在陌生感，可能不会完全吸收教师的授课内容。学生主要依据自身的知识储备进行学习。随着学习的深入，学生逐渐克服陌生感，进入学习舒适区，通过与教师之间建立的默契，可以迅速缩短与教师之间的差距。然而由式（1）中学生的新状态总是完全依赖自身的知识状态，这样设计可以简化进化过程，降低学生状态更新的复杂度，但与现实情况相比存在些许偏差。故加入自适应学生更新因子，将式（3）与式（4）修改为式（9）：

其中，是非线性自适应学生更新因子，为最大迭代次数，为当前迭代次数，为班级个体平均适应度值。由式（10）可知，在算法迭代初期接近1，此时式（9）中学生对于自身知识状态几乎全部保留。学生有更多的自我探寻机会，可以扩大学生的探索区域，具有较强的全局搜索能力。随着算法的不断迭代，不断减小，此时学生将降低对自身状态的保留程度，吸收教师的优点，从而迅速提升自身。同时算法的局部开发能力增强，其收敛速度和寻优精度也得到相应的提高。

2.5 结合社会心理学理论改进的教与学优化算法流程

将社会心理学理论加入到教与学优化算法中，依据理论改进教阶段和学阶段，同时加入自我学习方法调节阶段就构成了基于社会心理学理论改进的教与学优化算法。以最小优化问题为例，SPTLBO 算法基本流程如下：

（1）初始化阶段，在搜索空间内随机生成位学生，并计算所有学生的适应度值。比较每个学生的适应度值，选出最好的个体作为老师。

（2）教阶段，按照式（9）生成每个学生的新位置，计算新状态的适应度值，根据新状态是否优于原状态选择是否更新学生状态。

（3）学阶段，随机生成0-1 矩阵()，模拟场独立性（为1）和场依存性（为0）的学生，对其采取不同的学习策略，按照式（2）和式（5）进行。如果(X)＜(X)，则X代替X。

（4）自我学习方法调整阶段，计算此时全班适应度值1，选出优于全班平均值的个体为优秀个体，计算优秀集体的适应度平均值_。根据1 和_将班上学生分成三组，分别按照不同的学习策略进行学习，具体表述如式（6）～式（8）所示。

（5）检查结果是否满足算法停止规则，若符合则输出当前最优解并结束算法，若不符合则跳转至步骤（2）。

3 数值实验和结果分析

3.1 实验环境与参数

为了验证算法的性能，选取了10 个低维测试函数和15 个高维测试函数作为实验对象，共25 个。这些函数的函数名、表达式和理论最优值如表1、表2所示（低维见表1，高维见表2）。将提出的SPTLBO与TLBO、微粒群优化算法（PSO）、遗传算法（GA）和免疫算法（immune algorithm，IA）进行对比实验。本文的实验环境：计算机CPU 为i7-8586U，内存RAM为16 GB，操作系统为Windows10，编程软件为MATLAB2018a。

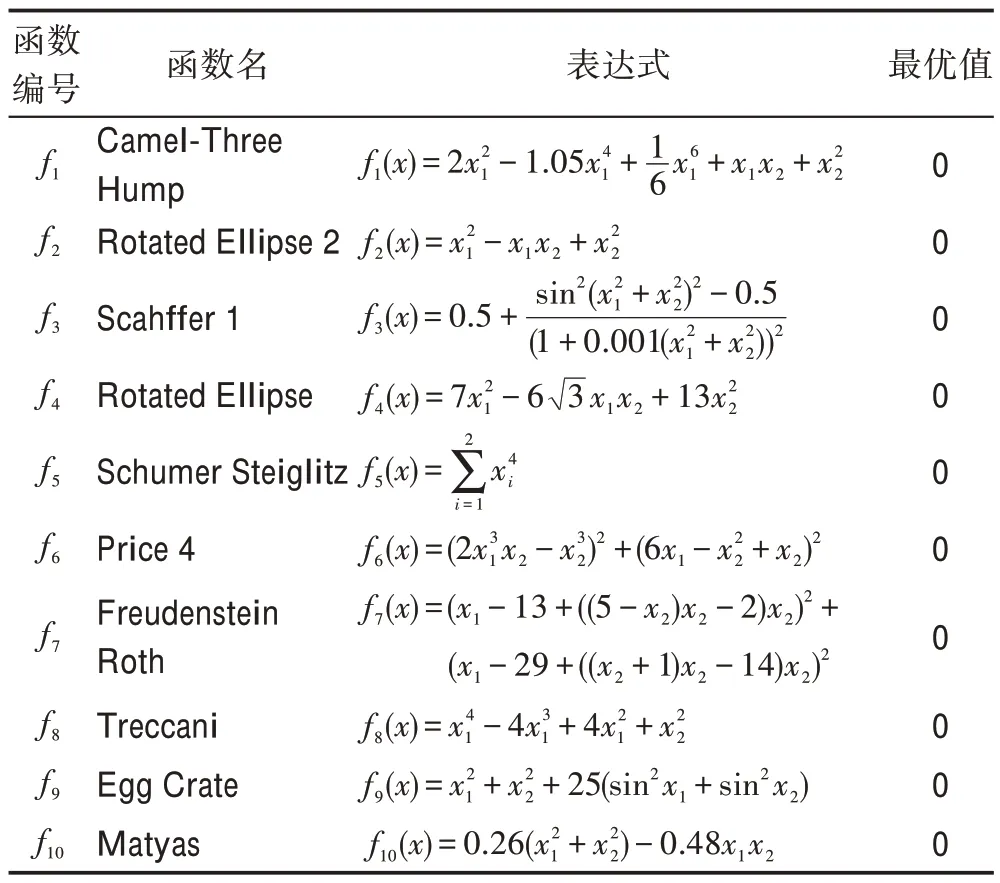
表1 低维测试函数Table 1 Low-dimensional test functions

表2 高维测试函数Table 2 High-dimensional test functions

SPTLBO 与对比算法的实验都是在最大适应度评价次数为15 000 下进行的。其种群数量都为50，最大迭代次数为300，低维测试函数的维度为2，高维测试函数维度为100。参考现有研究，对算法中其他参数设置如下：PSO 中学习因子==1.5，惯性权重=0.8；GA 中变异概率=0.1，交叉概率=0.8；IA 中变异概率=0.7，激励度系数==1。

3.2 实验结果与分析

本部分评估算法性能采用的是在相同的最大适应度评价次数下，评估算法的寻优精度。对于每个测试函数，SPTLBO、TLBO、PSO、GA 和IA 算法均独立运行30 次，分别得到最优解、最劣解、平均值和标准差，如表3、表4 所示。

从表3 与表4 可以看出，无论在低维还是高维的情况下，SPTLBO 算法在最优解、最劣解、平均值和标准差方面几乎都优于其他算法。当函数维度为2 时，从搜索精度来看，表3 中SPTLBO 算法指标都优于对比算法，其中，和各项指标均为最优值0。当函数维度为100 时，这对算法跳出局部最优和后期勘探新解的能力有了更高的要求。由表4 可知，对于、、、、、和，只有SPTLBO 搜索到最优值0；对于和，SPTLBO 每次运行都能搜索到最优值；对于，SPTLBO 前三项指标的精度略低于IA，但是对比两个函数的收敛速度（如图2（c）所示），可以发现SPTLBO 收敛最快，且最终搜索到最优值0；对于剩余测试函数，SPTLBO 搜索的结果精度远优于其他算法，同时通过不同测试函数在测试结果中的标准差可知，SPTLBO 具有较好的鲁棒性。

为了更加直观地显示SPTLBO 的优化精度和收敛速度，图2 与图3 分别展示了低维测试函数、、、和高维测试函数、、、的收敛曲线，其中函数纵坐标取以10 为底的对数。从图中可以看出，与其他算法相比，SPTLBO 算法收敛速度明显较快，搜索的精度也较高。

综合以上的对比结果，可以看出SPTLBO 算法的收敛速度和寻优精度均较为优秀。之所以如此，得益于在原始教与学优化算法中加入了社会心理学理论。在教阶段中加入的“期望效应”理论，如迭代方程（9）所示。规定均分以上的学生直接向教师学习，使得每次迭代都有一半学生向教师迅速靠拢，因此加快了粒子的收敛速度。在学阶段中加入的“场独立-场依存”理论，如迭代方程（2）与（5）所示。不同类型的学生采取不同更新策略，丰富了学阶段的更新方式，可以保持粒子的多样性，避免陷入局部最优。最后加入自我学习方法调整阶段，及时调整更新策略，如迭代方程（6）～（8）所示，使得算法的寻优性能与求解精度都得到了提高。

4 结束语

本文针对教与学优化算法在求解复杂优化问题时，寻优精度低、收敛速度慢等缺陷，从社会心理学角度出发，结合人的心理情绪变化，改进原始教与学优化算法。在教阶段引入社会心理学中“期望效应”理论，模拟教师对于优秀学生期望更高这一现象，使得适应度值较优的个体可以更快向最优个体靠拢；在学阶段引入“场独立-场依存”理论，模拟不同性格的学生对于汲取知识方式存在差异这一特点，从而更好地保留了结果的多样性，避免陷入局部最优；在学阶段后加入自我学习方法调整阶段，让个体根据自身排名采取不同的策略进行学习，从而有效地提高算法的寻优精度和收敛速度。为验证算法的性能，选取了25 个测试函数进行数值实验。结果表明，与原始的TLBO、PSO、GA 和IA 算法相比，本文提出的SPTLBO 算法在求解低维和高维函数时，不仅收敛速度快，而且寻优精度高，算法的稳定性也更强。由此可见在设计算法时，考虑人类心理因素对算法性能的提升有一定作用。目前教与学优化算法的改进很少考虑到关于人的因素，因此剖析人的心理在不同场景下的变化对于算法更深入的研究有着巨大意义。下一步的工作将深入研究心理学理论，寻找改进算法的切入点，使得算法性能更优。例如社会认知心理学中的“心理控制源”理论，该理论根据个体对于强化物或后果是否可以由自身控制，将心理控制源分为内控型与外控型。两者在相同情况下会做出不同的抉择。这一理论可应用于教与学算法的学阶段改进中，并推广解决动态车辆路径优化、各领域参数优化等更多复杂优化问题。

表3 低维测数函数结果对比Table 3 Comparison of experimental results of low-dimensional benchmark functions

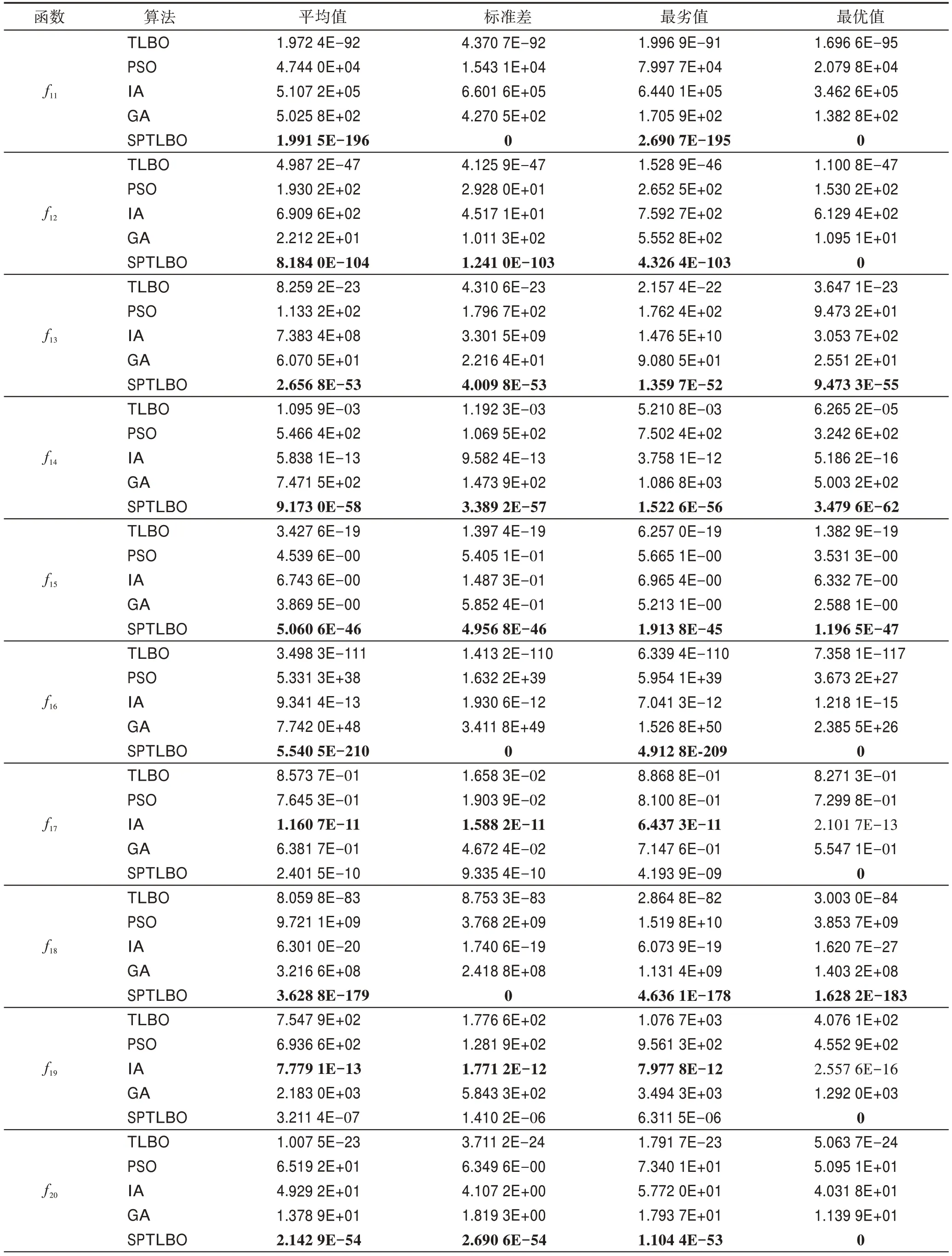
表4 高维测试函数结果对比Table 4 Comparison of experimental results of high-dimensional benchmark functions

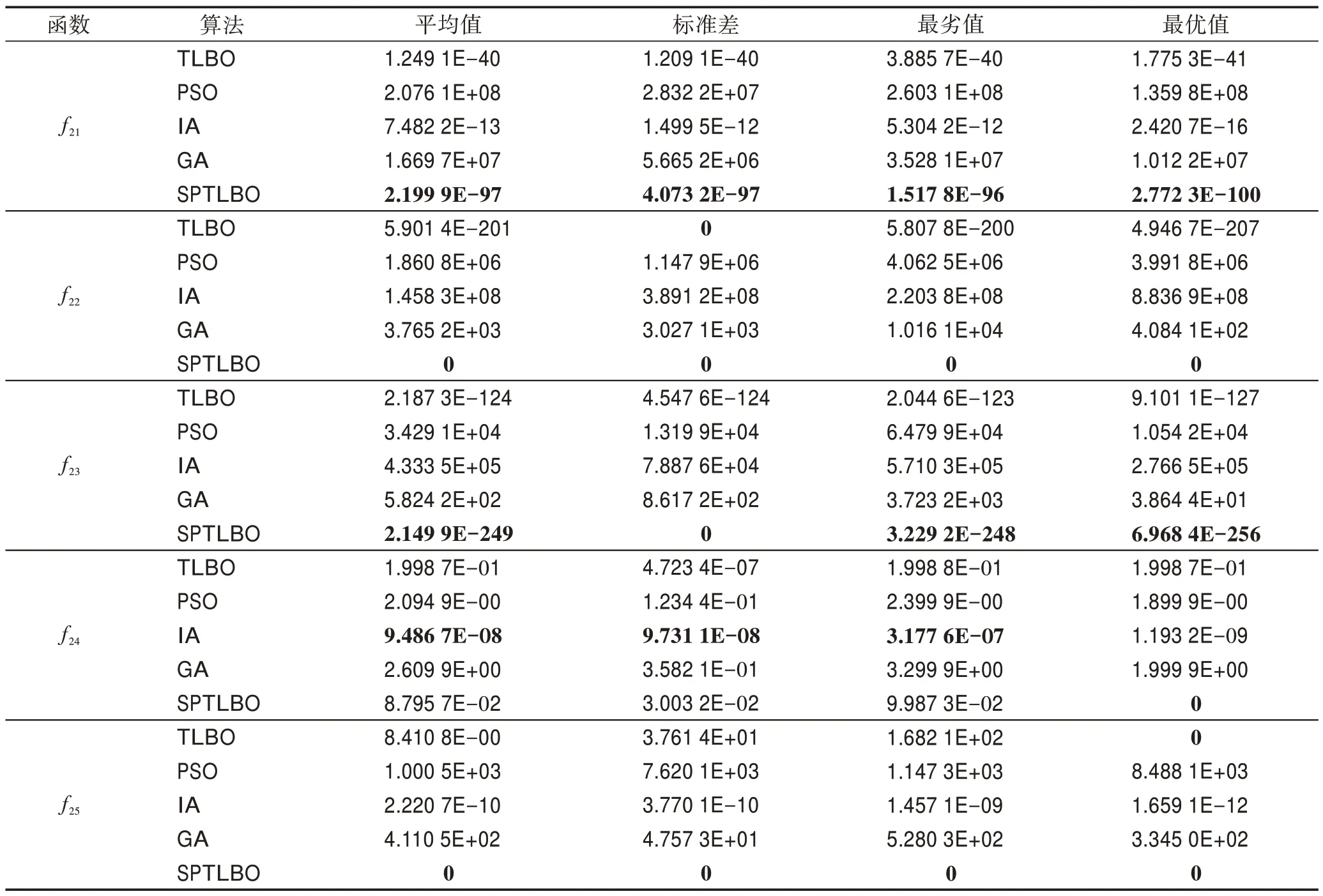
表4（续）

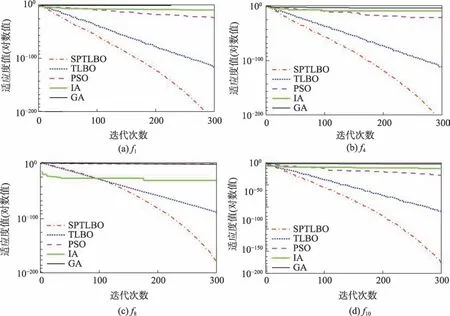
图2 低维收敛曲线对比Fig.2 Comparison of low-dimensional convergence curves

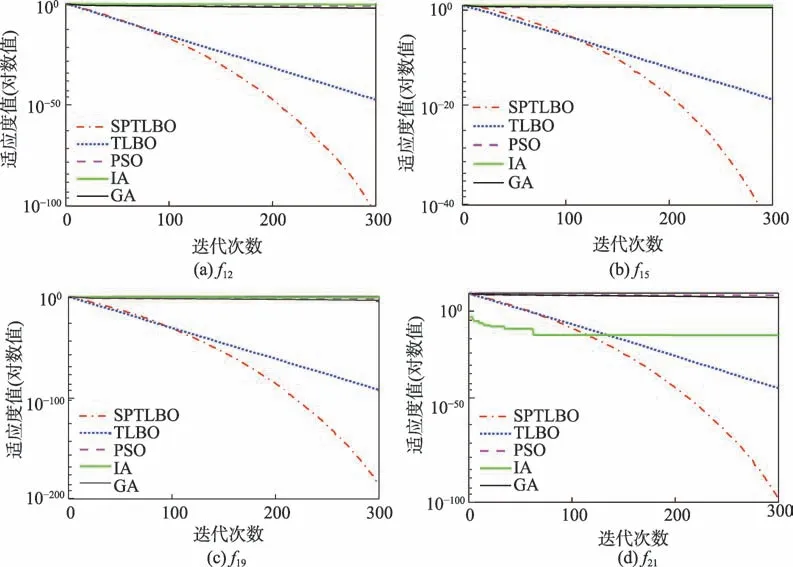
图3 高维收敛曲线对比Fig.3 Comparison of high-dimensional convergence curves