湿度对水化硅酸钙力学性能影响的分子动力学模拟

刘士达，李宗利,2，童涛涛，李云波，肖帅鹏

(1.西北农林科技大学水利与建筑工程学院，杨凌 712100；2.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100)

0 引 言

混凝土具有多尺度结构特征，不同尺度性能对混凝土宏观性能影响不同。混凝土材料的力学性能主要决定于水泥水化产物，而水泥水化产物中最重要的成分是水化硅酸钙(calcium silicate hydrate， C-S-H)凝胶体，占硬化水泥浆体体积的60%～70%，对水泥基材料的行为起着决定性的作用[1]。水化硅酸钙是水泥基材料组成的基本单元，其特性是解释混凝土宏观性能的基础。

水泥基材料经常服役于不同湿度的环境中，在水力梯度或自由吸水作用下，外界水进入使其处于不同的湿度状态。水泥基材料中的水分以多种形式存在[1-2]，按照水的存在形式，可以分为自由水、毛细水和层间水。其中，层间水是C-S-H层间吸附的水分子，与自由水和毛细水一起随湿度而变化。层间水对C-S-H力学性能的影响，一定程度上反映了湿度对水泥基材料的力学性能影响规律[3]。一方面，凝结硬化过程中层间水因水泥浆的初始含水量或水灰比大小在变化，从而影响水泥水合物的微观结构。另一方面，使用过程中层间水对周围环境和湿度也很敏感[4]，譬如，当浸入水中时，C-S-H凝胶吸水体积膨胀；当外界环境湿度降低时，C-S-H会脱去层间水，引起干燥收缩、断裂等微观结构的变化，从而影响C-S-H力学性能，而且不同受力状态影响机理也不同，因此，有必要研究不同受力状态下湿度对C-S-H力学性能的影响。

目前关于湿度对水泥基材料力学性能的研究大都基于宏观或细观尺度进行，微观或分子尺度下湿度对水泥基材料力学性能影响已有少量研究成果。张伟等[5]采用反应力场的分子动力学方法研究了缺陷内水分子对C-S-H性能的影响。得到的结果是初始缺陷内的水不仅自身会形成氢键，也会与C-S-H基体形成氢键，略微提高C-S-H的抗拉强度和弹性模量。Hou等[6]采用分子动力学方法研究了不同湿度C-S-H在单轴拉伸和单轴压缩下的力学性能。结果表明，湿度会降低C-S-H拉伸、压缩时的力学性能，且C-S-H的抗压强度远大于抗拉强度。Zhou等[7]对饱和度为0%～100%的C-S-H进行了不同应变率的单轴拉伸分子动力学模拟。计算结果表明，C-S-H的动态拉伸力学性能随着湿度的增加而降低。以上科研人员对不同湿度C-S-H的力学性能做了研究，然而仅仅针对的是C-S-H在受拉和受压状态下的力学性能。不同受力状态下C-S-H表现出的力学特性不同，湿度对不同受力状态下力学性能的影响程度也不同，需要进一步系统研究。

本文利用分子动力学，首先分析了不同湿度的C-S-H在结构和弹性参数上的差异，然后计算了不同湿度C-S-H在拉伸、压缩、剪切不同受力状态下的应力应变关系，对比分析了不同受力状态下湿度的影响程度，拓宽湿度对混凝土力学性能影响研究范围，系统揭示了纳观尺度下湿度对C-S-H力学性能的影响规律。

1 模拟方法

1.1 力场的选择和模型的建立

力场是表示分子系统势能变化的函数，选择合理与否影响着仿真精度的高低[8]。水化硅酸钙力场(CSHFF)是基于黏土力场(ClayFF)[9]开发的，主要通过改进ClayFF中Ca、Si和O的参数，使C-S-H的结构数据和高阶性质更加精确[10]。该力场已被证明可以正确预测实际水泥水合物的基本结构特征和基本物理特征，并且在C-S-H力学性能的分子模拟中已被广泛认可和应用[6,11-12]。因此，本研究选用CSHFF力场作为分子模拟的力场。通过文献[10]可获得CSHFF中描述Ca、Si、O、H原子间相互作用的参数。

本文基于Pellenq等[13]所提供的方法建立C-S-H模型。该方法基于Tobermorite模型删除部分SiO2所建立的“真实”模型能够很好地匹配实际C-S-H的各种参数，在C-S-H分子模拟中被广泛应用[6,8,14]。已有研究证明该模型能够很好地预测C-S-H的物理力学性能。模型建立的具体过程为：

(1)以Tobermorite 11Å晶体作为C-S-H模型的初始结构，根据核磁共振(NMR)测试提供的Qn分布进行断链[15]，即Q0=0%，Q1=66.01%，Q2=33.99%，平均链长(MCL=2(Q2/Q1+1)=3.03)与NMR测试结果保持一致，并参照Allen等[16]通过实验所测得的C-S-H的平均分子式，钙硅比采用1.7。然后在300 K、等温等压(NPT)系综下弛豫，得到干燥的C-S-H。

(2)采用蒙特卡洛方法对干燥的C-S-H进行吸水，吸附过程在300 K、NPT系综下完成，吸附步数设置为一亿步。将压强设置为饱和蒸汽压的一半，当吸附达到平衡状态时，得到湿度为50%的C-S-H；当吸附在饱和蒸汽压下达到平衡状态时，得到饱和状态下的C-S-H。最终建立的模型在分子式、密度、Qn物种分布和平均链长等方面与实验结果接近[15-16]。

(3)为了得到稳定统计结果，获得可靠的实效模式[17]，将上述建立的不同湿度的C-S-H模型扩展成1×3×4的超胞。湿度为0%的C-S-H超胞的尺寸为2.0 nm×7.8 nm×8.0 nm，含有8 616个原子；湿度为50%的C-S-H超胞尺寸为2.1 nm×8.2 nm×8.4 nm，含有11 892个原子；湿度为100%的C-S-H超胞的尺寸为2.2 nm×8.6 nm×8.8 nm，含有15 168个原子。

图1展示了不同湿度C-S-H的建立过程。

图1 C-S-H模型的建立过程Fig.1 Establishment process of C-S-H model

1.2 分子动力学模拟

受目前常用分子模拟软件分析功能限制，C-S-H弹性力学参数和不同受力状态的模拟分别采用不同软件进行。

C-S-H的弹性常数利用Materials Studio[18]软件进行计算。计算过程中通过对C-S-H结构施加应变，分析结构变形得到C-S-H的弹性常数。C-S-H的体积模量、剪切模量根据弹性常数和柔性常数，采用Voigt-Reuss-Hill平均值法计算，杨氏模量根据柔性常数进行计算。

LAMMPS(大规模原子/分子并行模拟器)是一个经过良好测试和广泛使用的开源经典分子动力学软件[19]，在模拟单轴拉伸和单轴压缩方面较为方便。对1.1节所建立的不同湿度C-S-H超胞模型进行充分弛豫，作为单轴拉伸、压缩模拟的模型。拉压沿平行和垂直于C-S-H的链状方向进行，即y和z方向。模型三个方向均采用周期性边界条件，模拟过程中对模型施加应变，应变速率保持0.08 ps-1不变。当沿一个方向进行拉伸或压缩时，其他两个方向的压力保持为零，变形自由，体现泊松效应。垂直于加载方向的无压力设置消除了对变形的人为约束，允许张力自由发展，不受任何约束[6]。整个系统的弛豫和模拟均在NPT系综下进行，模拟时间步长设置为1.0 fs。

C-S-H的剪切模拟也采用Materials Studio软件[18]完成。模拟剪切的模型采用1.1节所建立的C-S-H超胞。模型的三个方向均采用周期性边界条件，模拟过程中对超胞在y-z平面上施加剪应变，应变速率为0.005 ps-1。在每次施加完成后，对超胞进行弛豫，弛豫时间为10 ps，并将充分弛豫后的模型作为下一次施加的初始模型。剪切和弛豫过程均采用NVT系综，模拟时间步长设置为1.0 fs。每施加一次应变，都会得到一个相对应的剪应力，从而得到剪切时的应力和应变曲线。通过梯形积分规则计算应力应变曲线下的面积，得到拉伸、压缩和剪切时的单位体积应变能密度，用应变能密度作为评价系统变形性能的间接指标。

2 结果与讨论

2.1 不同湿度C-S-H结构及弹性常数的差异

图2 不同湿度C-S-H超胞Si—O、Cas—O、 Caw—O径向分布函数Fig.2 Radial distribution functions of Si—O, Cas—O and Caw—O in C-S-H supercell with different humidity

径向分布函数(RDF)可以解释为系统的区域密度与平均密度的比，反映微观结构变化。对1.1节所建立的不同湿度的C-S-H超胞模型进行充分弛豫后，计算层间钙与桥接氧Caw—O、层内钙与桥接氧Cas—O、硅原子与桥接氧Si—O的RDF，如图2所示。RDF的峰值所对应的位置表示两种原子之间的键长。本文所建立的不同湿度C-S-H模型中硅原子与氧原子的键长为(0.161±0.01) nm，层内钙与氧原子的键长为(0.231±0.02) nm，层间钙与氧原子的键长为(0.237±0.02) nm。Richardson[20]的实验数据显示，Si—O平均键长为0.164 nm，Ca—O键长在0.22～0.29 nm；X光散射实验[21]表明，Si—O平均键长为0.167 nm，Ca—O平均键长为0.243 nm；Svenum等[22]使用密度泛函理论计算得到C-S-H中Si—O平均键长为0.165 nm，Ca—O键长为0.23～0.25 nm。由此可见，本文所建模型的Ca—O和Si—O键长与实验数据和密度泛函理论数据一致，说明模型具有可靠性。

不同湿度C-S-H的RDF峰值出现在同一位置，说明湿度并不影响C-S-H中Si—O、Cas—O、Caw—O的键长。虽然峰值出现在同一位置，但是峰值大小却存在差异。随着湿度的增加，Si—O、Cas—O、Caw—O的RDF峰值不断增大，说明水分子的增加使得Si、Ca原子在近程范围内集聚的氧原子数更多。

图3为三种原子在z方向的原子浓度分布。取4～6 nm的部分晶胞进行分析对比。从图3可以看出，C-S-H在z方向呈现分层结构，以钙硅链和层间区域交替出现。Si原子和Cas原子组成钙硅链，Caw原子主要分布在两条钙硅链的层间区域。每个Cas和Caw原子峰值的出现，都伴随着两个Si原子峰值的出现，且

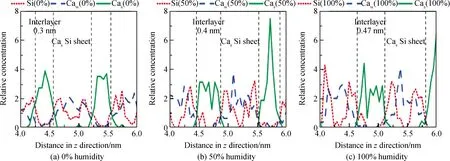
图3 不同湿度C-S-H超胞Si、Cas、Caw原子浓度分布Fig.3 Density profiles of Si， Cas， Caw atoms in C-S-H supercell with different humidity

Cas原子的峰值出现在Si原子的两个峰值中间，这说明钙硅链由两条硅链组成，且Cas原子分布在两条硅链中间。这与图1中C-S-H模型所显示的结构一致。虽然不同湿度的C-S-H的结构一致，但是随着湿度的增加，层间区域的宽度从0.3 nm增加到0.4 nm再增加到0.47 nm。这说明水分子的进入增大了C-S-H的层间距离，使得C-S-H的分层结构更加明显。

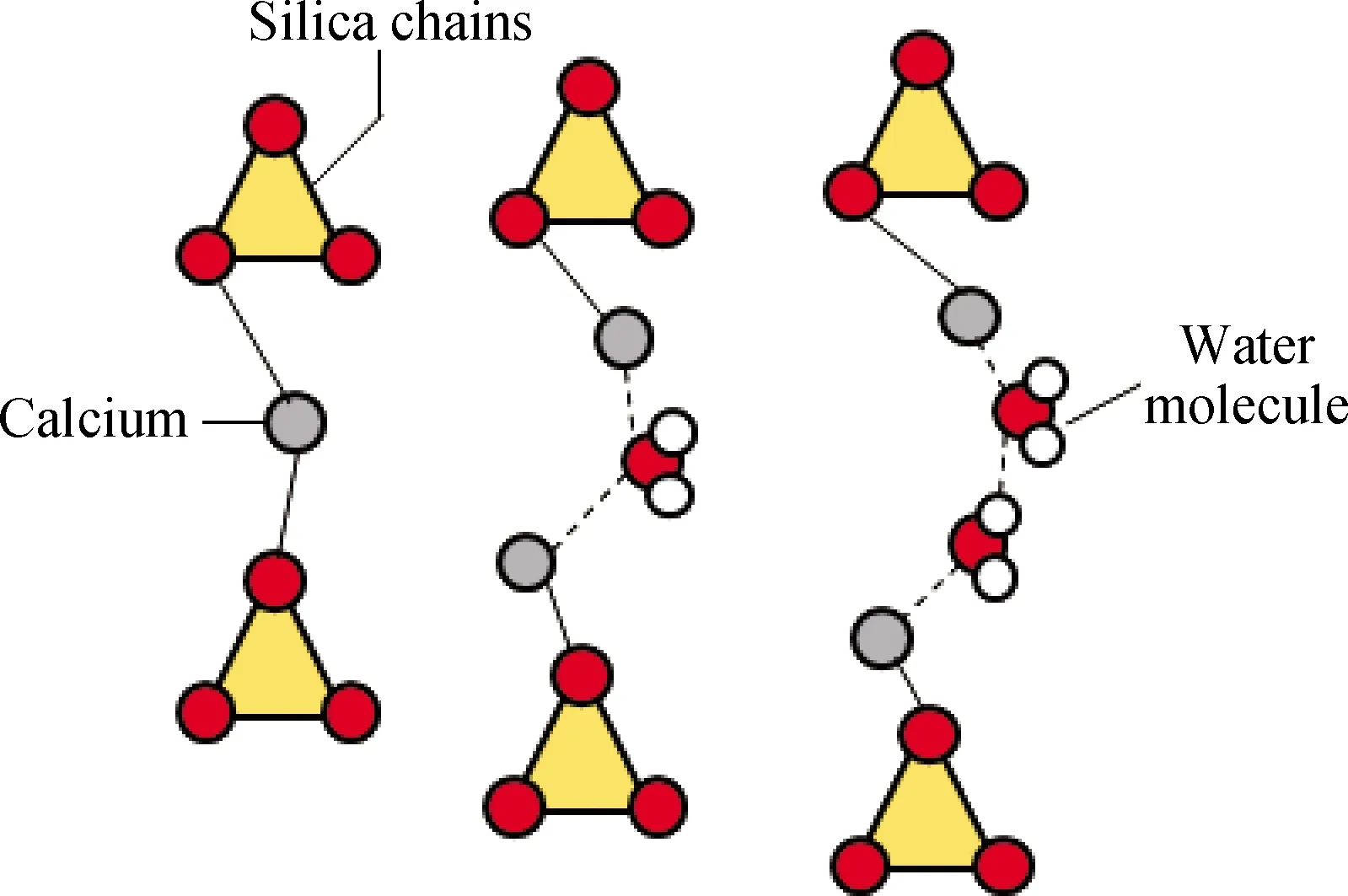
图4 层间连接示意图[6]Fig.4 Schematic diagram of interlayer connection[6]

将图3揭示的规律，采用图4表达，图4为C-S-H的层间连接示意图[6]。(1)湿度增加会导致C-S-H层间距离变大，体积增加，密度减小，受力时更容易变形。(2)湿度为0%时，硅氧四面体中的O原子与Ca原子跨层连接上下两个钙硅层，随湿度增加，首先层间水分子的O原子与Ca原子成键，当湿度进一步增大时，层间又有更多水分子之间的氢键，使得相邻的钙硅层间较强作用的Si—O键和Ca—O键逐渐被相对较弱的氢键分隔，C-S-H的强度也被削弱。因此，湿度会对C-S-H的力学性能产生重要的影响。

采用1.2节所介绍的方法得到不同湿度的C-S-H的弹性常数,见表1。表中KVoigt、KReuss、KHill分别代表Vogit、Reuss、Hill三种方法所计算的体积模量，GVoigt、GReuss、GHill分别代表Vogit、Reuss、Hill三种方法所计算的剪切模量，Ex、Ey、Ez分别代表三个方向的杨氏模量。从表中可以看到，随着C-S-H湿度的增加，其体积模量、剪切模量以及三个方向的杨氏模量均不同程度的下降，这说明水分子的侵入会降低C-S-H的弹性性质。Pellenq等[13]通过分子动力学模拟得到湿度为100%时C-S-H的体积模量和剪切模量分别为51 GPa和24 GPa；Abdolhosseini等[23]模拟得到湿度为100%时C-S-H的杨氏模量为67～80 GPa；Hajilar等[24]模拟湿度为100%的C-S-H的体积模量为56 GPa，剪切模量为27 GPa，杨氏模量在69 GPa左右。通过以上对比说明本文所计算的弹性常数具有一定的可靠性。

表1 不同湿度C-S-H超胞的弹性常数Table 1 Elastic constants of C-S-H supercell with different humidity

2.2 不同湿度C-S-H的应力应变关系

图5为不同湿度的C-S-H单轴拉伸时的应力应变曲线。从图中可以看出，C-S-H在拉伸时，初始阶段应力随着应变近似线性增加；当应力达到峰值时，应力开始缓降，即出现软化特性。应力应变关系在两个方向上存在很大的差异。沿y轴拉伸时，湿度为0%和50%的C-S-H并没有明显的软化特性，即使应变达到0.8时，应力也始终不为零，而湿度为100%的C-S-H在应变达到0.6时，应力减小为0，说明C-S-H已经被拉断；沿z轴拉伸时，湿度为0%的C-S-H不会被拉断，而湿度为50%和100%的C-S-H在应变分别达到0.55和0.4时会被拉断。这说明随着湿度的增加，C-S-H拉伸时的力学性能和变形能力不断下降，并且对z方向的影响要大于y方向。沿y方向拉伸时，湿度为0%、50%和100%的C-S-H的弹性极限应变分别为0.048、0.048、0.040，沿z方法拉伸时均为0.040。在弹性阶段内进行线性拟合，根据斜率计算y和z方向的弹性模量。三种湿度的C-S-H在y方向的弹性模量分别为77.6 GPa、56.6 GPa、50.5 GPa，z方向的弹性模量分别为70.4 GPa、55.5 GPa、48.0 GPa。显然随着湿度的增大，受拉弹性模量不断减小。在此需要说明的是该方法得到的受拉弹性模量与Materials Studio软件提供的方法所得计算结果(见表1)存在一定差异，这是由计算原理不同造成的，但湿度影响规律一致。

图5 C-S-H单轴拉伸应力应变关系曲线Fig.5 Stress-strain relation curves of C-S-H during uniaxial tension

如图6所示，C-S-H单轴压缩时的应力应变关系在两个方向上也存在不同。沿y轴压缩时，初始阶段应力随应变近似线性增加，三种湿度的极限弹性应变分别为0.048、0.048、0.040。湿度为0%的C-S-H在应力达到峰值后，应力不会减小，反而缓慢增加，表现出强化特性，湿度为50%和100%的C-S-H在应力达到峰值后开始缓慢下降，表现出软化特性，最后趋于稳定；沿z轴压缩时，初始阶段应力和应变近似呈线性关系，三种湿度的极限弹性应变均为0.048。湿度为0%和50%的C-S-H会表现出强化特性，湿度为100%的C-S-H会表现出软化特性，最后趋于稳定。说明湿度的增加会降低C-S-H压缩时的力学性能，且湿度对抗压能力的影响要小于对抗拉能力的影响。三种湿度的C-S-H在y方向的受压弹性模量分别为88.9 GPa、82.3 GPa 80.7 GPa，在z方向的受压弹性模量分别为57.6 GPa、55.3 GPa、49.5 GPa，受压弹性模量随湿度的增加而降低。其规律与Materials Studio软件提供方法计算结果(见表1)相同，但值存在差异。另外，由于受力变形特性不同，与拉伸时结果也存在差异，说明C-S-H拉、压弹性模量是不同的。

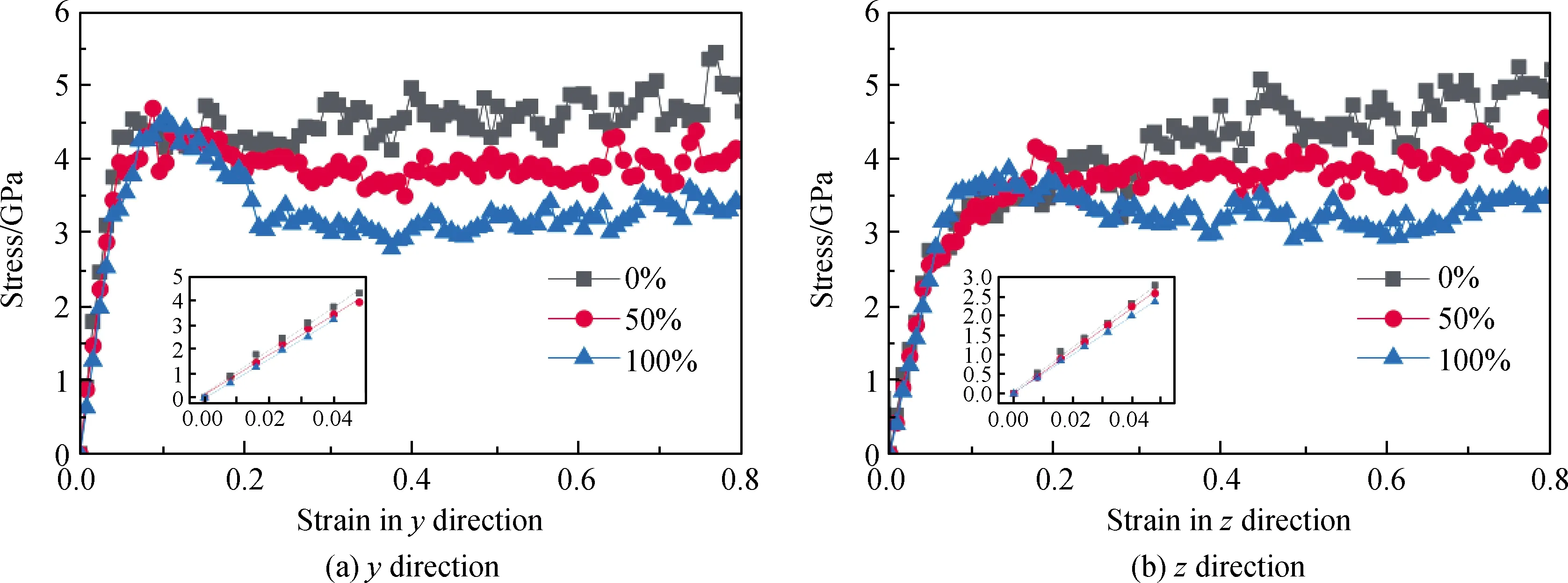
图6 C-S-H单轴压缩应力应变关系曲线Fig.6 Stress-strain relation curves of C-S-H during uniaxial compression

图7为不同湿度C-S-H剪切时的应力应变关系曲线。C-S-H在受剪时，初始阶段应力与应变近似呈线性关系，三种湿度的极限弹性应变均为0.035。当剪应力达到峰值后，应力呈锯齿状波动并缓慢增加，表现出强化特性。另外，随着湿度的增加，剪应力在不断下降。说明湿度的增加会降低C-S-H剪切时的力学性能，但影响程度也小于对抗拉性能的影响。根据弹性阶段的应力应变关系得到三种湿度的C-S-H剪切模量分别为19.7 GPa、17.4 GPa、13.5 GPa，表明随着湿度的增加，剪切模量逐渐降低。其规律与Materials Studio软件提供方法计算结果(见表1)相同，但值存在差异。

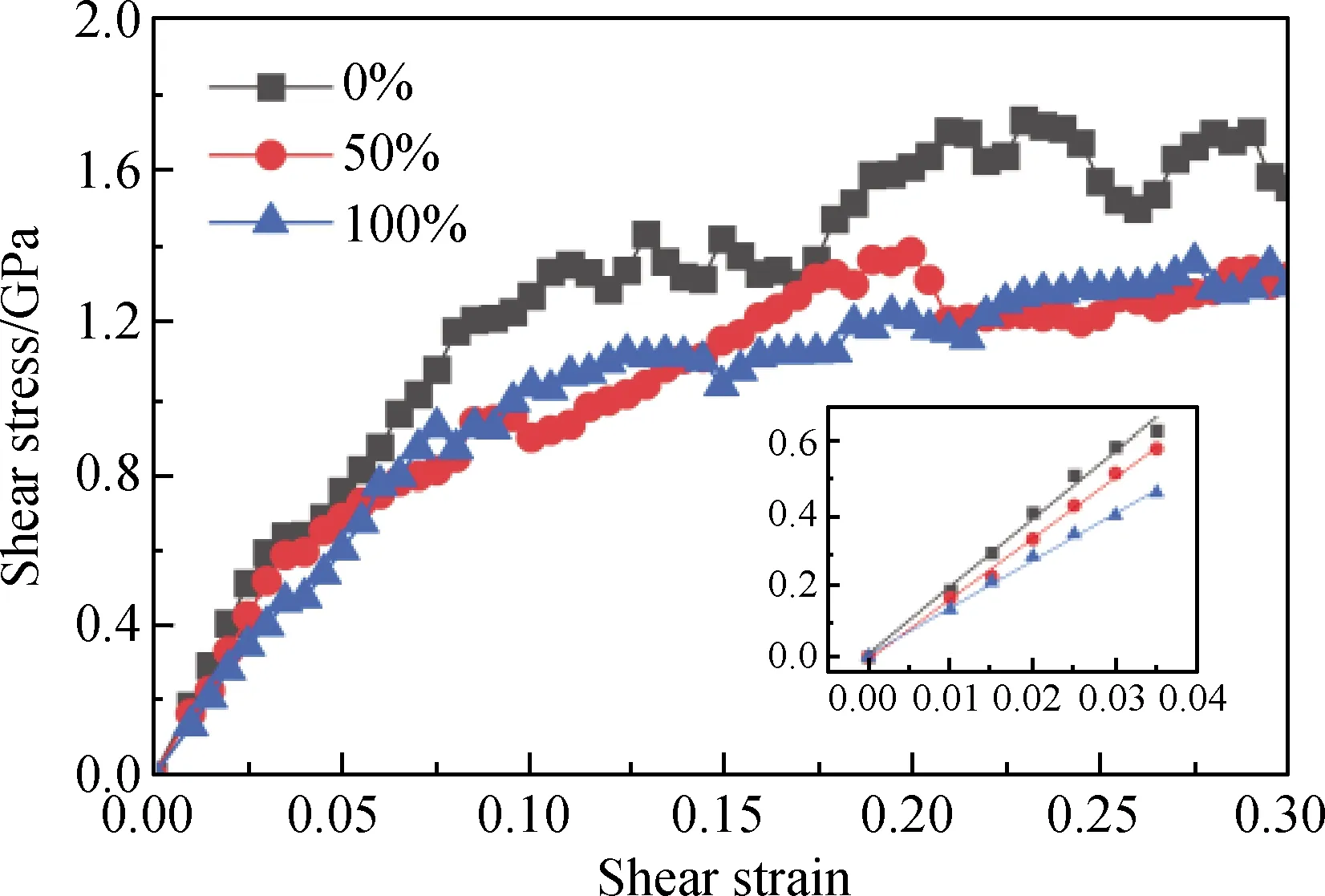
图7 C-S-H剪切应力应变关系曲线Fig.7 Stress-strain relation curves of C-S-H under shearing

以上通过对应力应变曲线的简单分析可以看出，湿度对C-S-H力学性能存在影响，同时，C-S-H在不同的受力状态下表现出不同的力学性能和变形性能。为了进一步分析湿度对不同受力状态下C-S-H力学性能的影响程度，表2列出了不同湿度的C-S-H在三种受力状态下的应力应变特征参数。从峰值应力的降低程度来看，当C-S-H的湿度从0%增加到50%和100%，在受拉状态下，y方向分别降低了4.90%和9.92%，z方向分别降低了6.56%和26.65%；在受压状态下，y方向分别降低了2.88%和4.01%，z方向分别降低了1.79%和9.59%；受剪时，分别降低了7.34%和21.96%。说明湿度对C-S-H抗拉与抗剪强度的影响较大，对抗压强度的影响较小。

应力应变曲线下的面积表示C-S-H的应变能密度，反映了C-S-H破坏前吸收的能量大小和变形性能。从应变能密度的降低程度来看，当C-S-H的湿度从0%增加到50%和100%，在受拉状态下，y方向分别降低了11.18%和53.11%，z方向分别降低了42.88%和68.29%；在受压状态下，y方向分别降低了11.06%和24.26%，z方向分别降低了10.55%和20.66%；受剪时，分别降低了20.16%和21.49%。说明湿度对C-S-H拉伸时的变形性能影响最大，其次是剪切，对压缩时变形性能的影响程度最小。

表2 不同受力状态下C-S-H的应力应变特征参数Table 2 Characteristic parameters of stress-strain of C-S-H under different stress states

3 结 论

(1)湿度增加使得C-S-H中Si、Ca原子近程范围内集聚的氧原子数更多，同时层间距离不断增大，分层更加明显；另外湿度会降低C-S-H的体积模量、剪切模量以及杨氏模量。

(2)湿度的增加会降低C-S-H单轴拉伸、单轴压缩和剪切时的力学性能和变形性能，对沿链状方向(y向)力学性能的影响弱于垂直链状方向(z向)。

(3)湿度对抗拉与抗剪强度的影响较大，对抗压强度的影响较小；对拉伸时的变形性能影响最大，其次是剪切，对压缩时变形性能的影响最小。