面向电力系统灵活性的电动汽车控制策略

姚一鸣 赵溶生 李春燕 燕智超 谢开贵

（1.输配电装备及系统安全与新技术国家重点实验室（重庆大学）重庆 400044 2.中国长江电力股份有限公司 宜昌 443133）

0 引言

随着碳中和目标的推进，我国可再生能源占比将逐年攀升。据估计，到2040 年，我国光伏装机量将增加16 倍、风电装机量将增加9 倍[1]。届时，我国电力系统中非水可再生能源的发电比例将高达30%[2]。可再生能源具有波动性和不确定性，其大量并网将给电力系统灵活性带来严峻挑战。“电力系统灵活性”指电力系统供需两侧响应系统不确定性变化的能力[3]，主要体现在调度运行环节，是衡量电力系统运行性能的重要指标之一[4]。电力系统灵活性不足将导致弃风和削负荷事件，严重威胁系统的经济安全运行。充裕的灵活性资源有助于缓解甚至消除可再生能源并网带来的负面影响，对于能源的可持续发展具有十分重要的意义。

电动汽车（Electric Vehicle,EV）作为一种新型交通工具，并网量逐年增加。预计到2030 年，电动汽车电池总容量将达57 亿kW·h，约为全网用电量的 1/3[5]。电动汽车是电力系统中的重要用电负荷，其可通过充放电控制调整自身负荷曲线，具有平抑可再生能源波动、提升系统灵活性的巨大潜力。

现阶段已有大量文献对电动汽车的充放电控制策略及其与可再生能源的协调调度进行研究。文献[6-13]以满足车主收益最大化需求或电力系统调度成本最低为目标，对电动汽车的充放电行为进行了详细的建模优化，但未考虑高比例可再生能源并网对电动汽车调度策略的影响。电动汽车与可再生能源协调调度的相关研究中，文献[14-18]基于日前风电、光伏的出力预测曲线，通过对电动汽车的充电价格进行优化或提供激励，改变电动汽车的充电负荷曲线，从而促进可再生能源的消纳。但可再生能源出力的实时波动很大，根据预测值制定的电动汽车控制策略难以应对电力系统实时运行过程中的动态灵活性需求。文献[19-21]针对可再生能源出力的时变性，建立了充电站的实时功率调整机制，以修正日前预测产生的偏差，但只计及了整个充电站的负荷曲线控制，未考虑充电站内不同电动汽车个体的功率特征和可调度性，导致制定的负荷调整方案过于乐观。文献[22-24]根据车主的偏好及出行计划提出了电动汽车有序充放电控制方案，在保障车主充电需求的同时尽可能满足电力系统调度指令，减少弃风弃光量，但其通过可再生能源实际出力与预测值的偏差来确定电动汽车的充放电控制量，无法全面刻画系统的灵活性需求。电力系统的灵活性需求是动态变化的，其大小取决于系统的运行策略，需考虑源、网、荷的交互影响，无法由可再生能源的出力波动量直接获取。

现阶段国内外对面向电力系统灵活性的电动汽车充放电控制研究仍属空白。电力系统灵活性匮乏是导致可再生能源消纳率低的主要原因[25]，传统的电动汽车充放电控制策略没有计及系统的动态灵活性需求，阻碍了电动汽车灵活性调节潜力的充分挖掘，影响了可再生能源的消纳效果。鉴于此，本文对面向电力系统灵活性的电动汽车控制策略进行研究。提出电力系统和电动汽车的灵活性定义。设计了电动汽车灵活性调度方案：各充电站对其能提供的最大灵活性进行评估；电力系统调度中心根据各充电站上报的最大灵活性信息，对系统的灵活性需求进行计算，并向充电站发布灵活性调度指令；各充电站再对站内电动汽车进行灵活性控制。通过电力系统调度中心、充电站和电动汽车的实时信息交换互动，最大化地满足系统的动态灵活性需求。最后，通过算例测试验证了本文所提电动汽车灵活性调度方案的有效性和优越性。

1 灵活性定义

1.1 电力系统灵活性

本文将电力系统灵活性定义为“系统运用自身资源禀赋应对可再生能源变化的能力”。本文考虑的可再生能源类型为风电。灵活性具有方向，且需在一定时间尺度下描述。根据方向的不同，灵活性可分为两类：向上灵活性和向下灵活性。向上（下）灵活性指风电突然减小（增加）时系统最大能增加（减小）的净出力功率。其中，净出力功率指常规机组总发电功率和负荷总需求功率的差值。根据时间尺度的不同，灵活性可分为调频灵活性（秒级）、爬坡灵活性（分钟级）和调峰灵活性（小时级）等。本文研究的灵活性时间尺度为15min，主要针对爬坡灵活性。随着风电渗透率的增加，充裕的电力系统灵活性变得越发重要。向上（向下）灵活性不足将导致切负荷（弃风）事件，严重威胁电力系统的经济安全运行。

1.2 电动汽车灵活性

本文将电动汽车灵活性定义为“电动汽车利用充放电控制调整自身用电负荷的能力”。电动汽车所能提供的最大向上（向下）灵活性指其通过充放电控制最大能满足的电力系统向上（向下）灵活性缺额。电动汽车有G2V 和V2G 两种控制模式。G2V控制是指电力系统通过调节并网后的电动汽车各时刻充电功率的大小来改变负荷侧总需求；V2G 控制是指与电网连接的电动汽车从其电池中输送功率给电网。电力系统向上灵活性不足时，电动汽车可通过G2V 控制减小充电功率或通过V2G 控制向电网放电；电力系统向下灵活性不足时，电动汽车可通过G2V 控制增加充电功率。合理的电动汽车充放电控制有助于增强电力系统灵活性，减少或者避免弃风、削负荷事件的发生。

2 灵活性调度方案

合理的电动汽车灵活性调度方案在保证车主利益的同时，也能提升电力系统的灵活性。本文设计的灵活性调度方案如图1 所示。

图1 灵活性调度方案 Fig.1 Flexibility dispatch scheme

概述如下：

1）最大可提供灵活性计算。各充电站对站内的电动汽车状态进行统计，计算出下个时刻所能提供的最大向上、向下灵活性信息，并告知电力系统调度中心。

2）电力系统灵活性需求计算。电力系统调度中心根据各充电站上报的下个时刻可提供的最大灵活性信息，通过滚动优化的方法计算需要调度的灵活性资源，并向充电站发布灵活性调度指令。

3）电动汽车灵活性控制。各充电站对站内电动汽车进行灵活性控制，参与控制的电动汽车车主根据实际调度情况获得相应的补贴。

3 数学建模

本部分将对灵活性调度方案中涉及的数学模型进行描述。模型中功率以kW 为单位，电量以kW·h为单位。

3.1 最大可提供灵活性计算

3.1.1 电动汽车模型

定义第v台电动汽车在t时刻的荷电状态为SOCv,t，表达式为

式中，Ev,t和分别为电动汽车的剩余电量和额定电量。

任一电动汽车v进入充电站后，充电站会告知车主参与电网灵活性控制的单位补贴价格τ（¥/kW·h）。车主结合自身行驶意愿等实际情况，给充电站提供如下信息：初始荷电状态，取车时间Cv，期望荷电状态，最低容忍荷电状态和损失厌恶系数λv。初始荷电状态是指电动汽车到达充电站时的荷电状态。取车时间经转换后以min 为单位，若2h 后取车，则取车时间设置为120min。期望荷电状态是指车主在取车时希望达到的荷电状态，需满足式（2）的约束，其中，为电动汽车v在t时刻的最大充电功率。由于参与灵活性控制会得到补贴，且车主今日的行驶意愿可能并不强烈，并不要求取车时电动汽车达到期望荷电状态，故引入“最低容忍荷电状态”的概念。最低容忍荷电状态是指车主能承受的电动汽车荷电状态下限，其取值范围约束如式（3）所示。其中，SOCmvin表示为了保障电动汽车v电池健康及行驶需求所要求的最低电量。参与控制的车主在取车时获得的补贴为。其中，是指取车时电动汽车v的实际荷电状态，其值需满足式（4）的约束。损失厌恶系数λv刻画了车主在面对取车时实际荷电状态与期望荷电状态之间差距的满意度，其取值范围在本文中设定为[0,1]。当λv=0时，表示车主非常愿意参与电网的灵活性控制从而获取补贴收益；当λv=1时，表示车主希望尽可能将电动汽车充电至期望荷电状态，对于获得补贴的敏感度很低。

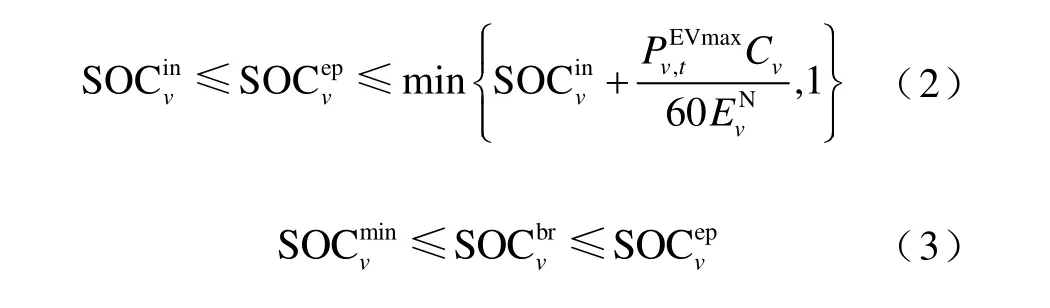
3.1.2 电动汽车状态统计

假设某充电站h中停有辆电动汽车。该充电站对 15min 后站内所有电动汽车的状态进行统计，并计算届时本充电站所能提供的最大向上（向下）灵活性。

对于电动汽车v，充电站将求解目标函数为式（5），约束式为式（6）～式（8）的优化问题以确定其15min 后的状态。

式中，δ为惩罚因子；βv为期望荷电状态与充电站最多能使电动汽车达到的荷电状态的差值；ρt为电价[¥/(kW·h)]；为电动汽车v在t时刻的充电功率；为当前时刻；为取车时刻；为向下取整操作。本文t时刻和t+1 时刻的差距为15min。目标函数式（5）由两部分组成：第一部分为惩罚项，旨在督促充电站尽可能在取车时间前使电动汽车达到车主的期望荷电状态；第二部分表示充电站给电动汽车充电的电费成本。

约束式（7）和式（8）限制了βv和电动汽车充电功率的范围。

对所有电动汽车并行求解上述优化问题，充电站将获得各电动汽车的计划充电功率信息和荷电状态。接下来充电站将计算其所能提供的最大向上（向下）灵活性。

3.1.3 最大可提供向上灵活性计算

电动汽车的G2V 和V2G 模式均可用于提供向上灵活性资源。G2V 控制模式下，充电站可减少给电动汽车的充电功率，以削减负荷需求。对于电动汽车v，其在时刻最大能减少的充电功率可通过求解优化问题（9）获得。

3.1.4 最大可提供向下灵活性计算

电动汽车只有G2V 模式可用于提供向下灵活性资源。在G2V 控制模式下，充电站将按照最大充电功率给电动汽车进行充电，以增加负荷需求，充电站h在时刻使用G2V 控制所能提供的最大向 下灵活性。

3.2 电力系统灵活性需求计算

采用滚动优化方法[26]对电力系统的灵活性需求进行建模，目标函数为

式中，NG为火电机组总数；Tpr为下一时段；T为总时段数，本文时间尺度为15min，故共有96 个时段；a、b、c、cu、cd为火电机组的成本系数；Pi,t为第i台火电机组在t时刻的计划出力功率；分别为火电机组的运行/起动/停机状态（若运行/起动/停机，则值为1；否则值为0），其值由日前机组组合计划确定，在实时调度模型中作为输入参数；NW为风电场总数；NEB为除电动汽车外的常规电负荷总数；λ和μ分别为弃风和切负荷的单位成本；和分别为计划弃风功率和切负荷功率。

式（12）～式（14）为机组出力约束。

弃风和切负荷功率约束为

式中，ΩW为风电场的集合。

线路潮流约束为

式中，PFn,m为线路传输容量的上限；ΨE为电力传输线路集合。式（19）限制了平衡节点处的相角θref,t为0。式（20）～式（23）限制了充电站充电负荷的取值范围。

3.3 电动汽车灵活性控制

3.3.1 车主满意度排序

本文引入经济学中“损失厌恶（Loss aversion）”的概念来刻画电动汽车车主参与灵活性控制的积极性。人们在不同环境下的决策行为并非完全理性,往往表现出对损失比对盈利更为敏感的现象，这种非理性决策行为就被称为损失厌恶。使用文献[27]中提出的模型对车主的损失厌恶心理进行建模。

式中，gv为第v台电动汽车车主的心理满意度，其取值范围为[0,1]，值越大代表车主越满意。可根据gv值的大小对电动汽车进行优先级排序，根据排序结果先后参与灵活性控制。详细的灵活性控制计划如下所述。

3.3.2 向上灵活性控制

若充电站h在t时刻需提供值为的向上灵活性，从保护电池的角度出发，充电站将首先安排电动汽车参与G2V 控制。G2V 控制策略如下：

1）将t时刻所有与电网连接的电动汽车按照满意度进行降序排列，得到集合ΩG2Vmax，NG2Vmax为该集合的元素个数。

解得nG2V的值后，取集合ΩG2Vmax中前nG2V个元素构成新集合ΩG2V，即为参与G2V 控制的电动汽车集合。充电站将对集合ΩG2V中的前nG2V-1辆电动汽车供给值为的功率，对第nG2V辆电动汽车供给值为的功率。此时可以满足电力系统调度中心分配的向上灵活性需求任务。

若G2V 控制不足以完成灵活性任务，此时需启用V2G 控制，策略如下：

1）将t时刻所有与电网连接的电动汽车按照满意度进行降序排列，得到集合ΩV2Gmax，NV2Gmax为该集合的元素个数。

2）求解优化模型

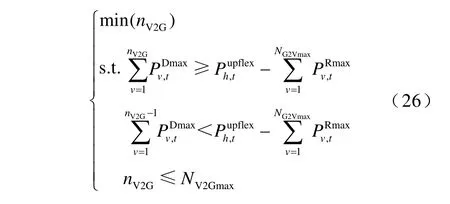
解得nV2G的值后，取集合ΩV2Gmax中的前nV2G个元素构成一个新的集合ΩV2G，即为参与V2G 控制的电动汽车集合，该集合中的前nV2G-1辆电动汽车将向电网输送值为的功率，第nV2G辆电动汽车向电网输送值为的功率。此时可以完全满足向上灵活性需求任务。

3.3.3 向下灵活性控制

若充电站h在t时刻需提供值为的向下灵活性，充电站将安排电动汽车参与G2V 控制。G2V控制策略如下：

1）将t时刻所有与电网连接的电动汽车按照满意度进行升序排列，得到集合为该集合的元素个数。

2）求解优化模型

4 算例分析

本节将设计算例来验证本文模型的优势和有效性。所有的算例测试都在8G 内存，Intel(R) Core(TM) i7-7700 CPU @ 3.60GHz 的计算机上，使用Python 3.7 调用求解器Gurobi 9.0.1 完成。本文时间尺度为15min，实时调度过程中共有96 个时间段。

4.1 24 节点系统

首先，以24 节点电力系统为例对本文所提电动汽车灵活性调度方案进行详细分析。电力网络采用IEEE RTS-24 节点系统[28]进行模拟，该系统中有17个负荷节点，假设每个负荷节点都接有10 个电动汽车充电站，整个系统需要满足170 个充电站的电力需求。三个风电场分别接在节点3、5 和20 处。考虑四种风电场景（分别代表四个季节），风电出力的预测值和实际值如附图1～附图4 所示。对应于四个季节的常规电负荷场景如附图5 所示。各充电站每时刻新增的电动汽车数量满足正态分布。抵达充电站的电动汽车电池容量均设置为30kW·h，最大充放电功率为12kW，初始荷电状态满足在区间[0.2,1]上的均匀分布[7]，电动汽车的最低容忍荷电状态设置为0.35[29]，电动汽车取车时间服从正态分布，参与电网灵活性控制的补贴为0.5¥/(kW·h)，车主的损失厌恶系数服从在区间[0,1]上的均匀分布。

4.1.1 电力系统灵活性分析

为评估本文提出的电动汽车控制策略对提升电力系统灵活性的作用，考虑如下两种情况：①电动汽车不参与灵活性控制；②电动汽车参与灵活性控制。

在这两种情况下，就四种不同的场景分别对电力系统的灵活性缺额进行计算，结果见表1。

表1 24 节点系统灵活性缺额计算结果 Tab.1 Calculation results of the flexibility shortage in the 24-node power system

由表1 可见，通过本文提出的电动汽车灵活性控制策略，电力系统的向上灵活性缺额和向下灵活性缺额都大大减少。情况②的场景3 下，电力系统灵活性缺额为0，这主要是因为场景3 的风电资源较为匮乏，出力一直维持在较低的水平，其产生的波动可被电动汽车的充放电控制完全平抑。从表1中还注意到电力系统的向上灵活性缺额远小于向下灵活性缺额，这是因为电动汽车可通过G2V 和V2G两种控制模式提供向上灵活性资源，而向下灵活性资源只能由G2V 模式提供。情况②中电动汽车参与G2V 控制和V2G 控制的能量见表2。

表2 G2V 和V2G 控制能量 Tab.2 G2V and V2G control energy

由表2 可知，电动汽车参与G2V 控制的能量远大于参与V2G 控制的能量，这主要是由于G2V 模式既能提供向上灵活性的需求，又能提供向下灵活性的需求，且在应对系统向上灵活性需求时，G2V模式比V2G 模式有更高的优先级。

电力系统调度中心可通过从电力市场中购买辅助服务来满足灵活性缺额。美国CAISO 市场2021年3 月8 日上调和下调备用的日前预测价格曲线[30]如图2 所示。不同情况和场景下，为满足灵活性需求而购买辅助服务产生的费用见表3。由表3 可知，通过电动汽车的灵活性控制可大大降低电力系统的运行成本，证明了本文所提电动汽车控制策略的经济价值。

表3 购买辅助服务费用 Tab.3 Cost of purchasing auxiliary service

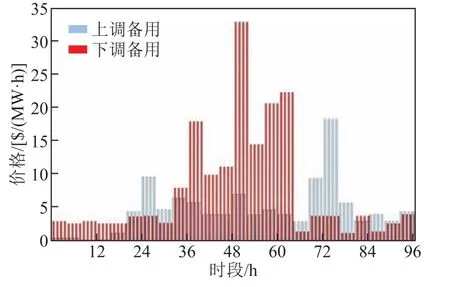
图2 备用价格 Fig.2 Regulation prices

4.1.2 计算时间分析

本文研究的灵活性时间尺度为15min，因此电动汽车的灵活性控制策略需在15min 内完成制定。使用蒙特卡洛模拟法抽取四个场景下电动汽车的状态各1 000 次，即模拟4 000 天的电动汽车灵活性 控制过程。图3 给出了这4 000 天内各时段充电站可提供灵活性、电力系统灵活性需求和电动汽车灵活性控制计算所需最大时间。

图3 24 节点系统计算时间 Fig.3 Computing time in the 24-node power system

由图3 可知，本文所提模型的计算时间完全能够满足15min 的灵活性调度需求。充电站最大可提供灵活性计算和电动汽车灵活性控制耗时均在0.2s内，这主要是因为相应的模型为线性规划模型，时间复杂度很低。电力系统灵活性需求计算模型为二次规划模型，故耗时略长，但也完全可以满足实际需要。由此可见本文所提电动汽车灵活性控制策略的实用性和有效性。

4.1.3 参数影响分析

表4 最低容忍荷电状态对灵活性的影响 Tab.4 Impact of the lowest tolerable SOC on the power system flexibility

4.2 实际系统

对中国西北某省的实际电力系统进行测试，以进一步证明本文所提方法在改善电力系统灵活性和计算时间上的巨大优势。该电力系统中含有93 个主要负荷节点，假设每个负荷节点都接有30 个电动汽车充电站，电动汽车的参数设置与24 节点相同。使用K-means 聚类算法生成四种典型风电出力和负荷场景，考虑的两种情况与4.1 节相同。不同情况和场景下的电力系统灵活性缺额计算结果见表5。由表5 可知，本文所提电动汽车灵活性控制策略可分别降低向上和向下灵活性缺额约80%和60%，大大减少了弃风和削负荷量。

表5 实际系统灵活性缺额计算结果 Tab.5 Calculation results of the flexibility shortage in the realistic power system

接下来对本文提出方法的计算时间进行评估。与4.1 节相同，使用蒙特卡洛模拟法模拟4 000 天的电动汽车灵活性控制过程。各时段充电站可提供灵活性、电力系统灵活性需求和电动汽车灵活性控制计算所需最大时间如图4 所示。由图4 可知，本文所提电动汽车灵活性控制方法的计算时间在秒级，完全可以满足实际需要。

图4 实际系统计算时间 Fig.4 Computing time in the realistic power system

5 结论

随着碳中和目标的不断推进，如何提高电力系统灵活性以适应可再生能源的实时波动，成为了亟须解决的问题。电动汽车作为一种新兴的可变负荷，可通过合理的充放电控制缓解电力系统灵活性不足的问题。本文从面向电力系统灵活性的电动汽车实时调度角度出发，研究了电动汽车的灵活性控制策略，设计了“最大可提供灵活性计算-电力系统灵活性需求计算-电动汽车灵活性控制”的灵活性调度方案。

基于各时刻充电站所能提供的最大灵活性计算结果，电力系统调度中心通过滚动优化的方法计算需要调度的灵活性资源，并向充电站发布灵活性调度指令，充电站进而对站内电动汽车进行灵活性控制。通过IEEE RTS-24 节点和实际电力系统算例测试，得出如下结论：本文所提的电动汽车控制策略能极大缓解电力系统的灵活性缺额，有助于减少弃风、削负荷量。另外，本文模型的求解时间为秒级，完全可以满足电力系统的实时灵活性调度需求，证明了模型的实用性和有效性。车主参与电网灵活性控制的单位补贴价格在本文中被假定为一个给定的常数，该价格的制定需综合考虑电网及车主的利益分配，其详细的制定方案将是本文的下一步研究方向。

附 录

附图1 场景1 下风电场出力预测值和实际值 App.Fig.1 Forecast and actual value of wind farm output in Scenario 1

附图2 场景2 下风电场出力预测值和实际值 App.Fig.2 Forecast and actual value of wind farm output in Scenario 2

附图3 场景3 下风电场出力预测值和实际值 App.Fig.3 Forecast and actual value of wind farm output in Scenario 3

附图4 场景4 下风电场出力预测值和实际值 App.Fig.4 Forecast and actual value of wind farm output in Scenario 4

附图5 常规电负荷预测值和实际值 App.Fig.5 Forecast and actual value of traditional electrical load