基于概率矩阵分解的不完整数据集特征选择方法

范林歌，武欣嵘，童 玮，曾维军

（中国人民解放军陆军工程大学 通信工程学院，南京 210007）

0 概述

高维数据在实际应用中普遍存在，这些数据通常被用来构建高质量的机器学习模型，随后进行数据挖掘分析，但高维数据具有计算时间长、存储成本高等问题［1-2］。为了解决这些问题，研究人员提出特征选择、主成分分析等降维方法［3-4］。特征选择是数据挖掘过程中的重要步骤，特别是在许多生物信息学任务中，有效的鲁棒特征选择方法可以提取有意义的特征并且消除有噪声的特征。

现有的特征选择方法大多以数据是完整的或几乎完整的为前提。但在许多实际应用中，例如生物信息学［5］和遥感网络普遍存在数据缺失，现有的特征选择方法大部分不能直接用于包含缺失值的数据集。

对不完整数据集进行特征选择，最直接的方法是对不完整数据集进行一定处理使其保持形式上的完整，然后再做特征选择。处理缺失数据最简单易行的方法是完整样本分析（Complete Case Analysis，CCA），即删除包含缺失值的样本或特征［6］。该方法虽然简单易行，但在缺失样本比例较高和样本总量较小时有很大的局限性，进而影响后续机器学习的准确性。对缺失位置进行填充是另一种较为直接的缺失数据处理方法，应用普遍的是均值填充。均值填充是指以特征观测值的均值作为缺失值的估计值［7］，但该方法会使特征不确定性或方差减小。还有一种基于统计学的缺失填补方法是期望最大化（EM）填补法［8］，该方法利用现有数据的边缘分布对缺失数据进行极大似然估计，从而得到相应的填补值。ZHANG 等［9］提出了k 近邻填充，该方法基于近邻样本的特征值相近的假设，以近邻样本的均值作为缺失值的估计值。之后一些改进的k 近邻填补方法被提出，其引入灰色关联分析和互信息来更进一步地提高分类精度和填补效果［10-13］。近邻填充的关键在于准确地度量近邻关系，这也带来了一些不足：不同的特征在相似度度量中的重要性是不同的，而k近邻填充中的距离计算将所有特征同等对待；当数据特征数目较多即在高维特征空间中时，样本分布趋于均匀，此时距离并不能反映样本相似性。

在不填充直接进行特征研究方面，LOU 等［14］提出基于类间隔的不完整数据特征选择（Feature Selection in Incomplete Data，SID）方法，定义了基于类间隔的目标函数，对其优化使每个样本在其相关子空间中的类间隔最大化，以权重范数比为系数降低缺失样本对于类间隔计算的贡献，该方法不再将某个样本的近邻样本当作是固定的，而是去计算所有样本是某个样本近邻样本的概率。SID 特征选择最终学习出一个特征权重向量w，w中取值较大的分量对应重要特征，取值较小的分量对应次要特征，取值为零的分量对应无关特征甚至噪音特征。与基于常用预处理填充方法（如均值填充、EM 填充、k 近邻填充）的特征选择相比，SID 能够筛除更多无关特征，以该算法选择的特征建立的分类模型分类准确率更高，但其没有考虑异常值的影响。

本文针对不完整数据中含有未被观察信息和存在异常值的特点，提出一种基于概率矩阵分解（Probability Matrix Decomposition，PMF）技术的鲁棒特征选择方法，使用指示矩阵并利用不完整数据集中的所有信息进行缺失值近似估计。在特征选择算法上基于鲁棒特征选择（Robust Feature Selection，RFS）方法，在损失函数和正则化项中联合使用ℓ2，1范数［15-16］，将ℓ2，1范数作为损失函数可减轻异常值影响，提升特征选择的鲁棒性。

1 基于矩阵分解的缺失值填充方法

考虑不完整数据集X={(xn，yn|n=1，2，…，N)}∈RM，其中N为样本数，M为特征数，xn为第n个给定实例，yn为其对应的标签值，yn=1，2，…，T，xn(j)表示第n个样本的第j个特征，其中j=1，2，…，M。

由于直接使用不完整数据集中所有实例来预估缺失值计算量较大，本文首先使用原始标签将原始数据集分簇，将相似度较高的样本分为一簇，假设第i簇数据集为Xi，每一簇数据集实例选择如式（1）所示：

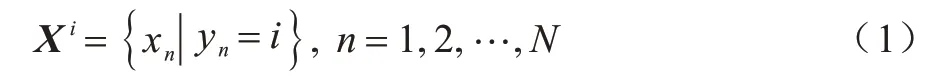
其包含L个实例，Xi具体表示如式（2）所示：

其中：q=1，2，…，L，表示第i簇数据集中第q个实例的第j个特征。

本文基于这样一个假设：同一簇内两个样本相似度比不同簇的两个样本高，以达到在减少计算量的基础上不降低填充准确性的目的，之后分别对每簇中的缺失值进行估计。

在计算过程中利用指示矩阵对未观察到的信息进行过滤，从而达到利用完整和不完整样本中所有有效信息的目的。对于给定的不完整数据集X，定义指示矩阵I，其中In（j）反映第n个实例的第j个特征的缺失情况，元素取值如式（3）所示，当xn(j)可观测时对应位置取1，当xn(j)缺失时对应位置取0。

则第i簇数据集Xi对应的指示矩阵为Ii。

1.1 矩阵分解

寻找第i簇数据集Xi的一个近似矩阵，通过求解近似矩阵来代替原始数据簇中缺失的值，定义如式（4）所示：

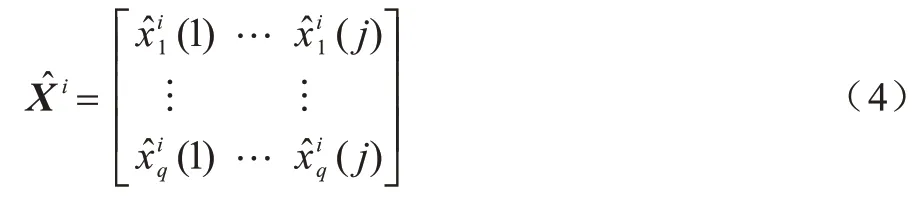
其中：U∈RL×K；V∈RM×K，矩阵U和V分别表示数据集实例和特征特定的潜在特征向量。比如在一个用户对多部电影评分的数据集中，xq(j)表示第q个用户对第j部电影的评分，此时U和V分别描述用户的特征（比如年龄段等）和电影的特征（比如年份、中英文等）。

均方根误差（RMSE）可以用来衡量真实值与预估值之前的差距，本文通过计算目标矩阵Xi与近似矩阵的RMSE 来评估模型性能，Xi与的RMSE定义如式（6）所示：

由式（5）得：

代入式（6）得：

RMSE 值越小则表示填补效果越好。本文通过求解一组U和V使相似矩阵与目标矩阵Xi的RMSE 最小，至此该优化问题可以表示为：

至此，将上述问题转化为一个无约束优化问题，本文采用梯度下降法［18］迭代计算U和V，首先固定V，对U求导，如式（10）所示：

更新uq，如式（11）所示：

其中：α为更新速率，表示迭代的步长。

固定U，对V求导得：

更新vj，如式（13）所示：

重复式（11）与式（13），迭代优化U和V，直到RMSE<ξ，ξ为自定义误差。

遍历所有i，对每一簇数据进行如上操作，直到Iο等于0 即数据集无缺失为止。至此，求出Xi的近似矩阵，用中的数据填充Xi中对应位置的缺失值。Iο定义如式（14）所示：

1.2 概率矩阵分解

为提升算法精度以及降低算法运算复杂度，本文将上述的矩阵分解扩展为概率矩阵分解。假设数据集第i簇数据集Xi，归一化后服从均值为μ=0，方差为σ2的高斯分布。因此，可定义U和V为一个多变量的零均值球面高斯分布，如式（15）、式（16）所示：

该先验概率可使式（11）和式（13）最终的收敛值不会远离0，从而避免了矩阵U和V出现幅度较大的值。若无该先验知识，1.1 节中的矩阵概率分解迭代运算次数将增加，运算复杂度提升。

综合上述两个先验概率，可将数据集X上的取值条件概率分布定义为：

基于式（15）、式（16）、式（17）的概率密度函数，利用经典的后验概率推导可以得到p(U，V|X)=p(X|U，V)p(U)p(V)，最大化该后验概率，就可以通过已有的近似矩阵估计出系统参数U和V。

为了计算方便，对后验概率取对数，在观测噪声方差和先验方差保持固定的情况下，最大化该对数后验分布等价于使用二次正则化项使误差平方和最小。最后，为了限制数据集中数据的取值范围，对高斯函数的均值施加logistic 函数g(x)=1/(1+exp(-x))，其取值在（0，1）之间。最终的能量函数为：

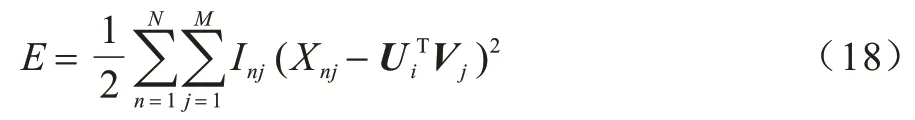
至此，可以使用梯度下降方法，求解Ui、Vj中的每一个元素。

2 鲁棒特征选择算法

2.1 鲁棒特征选择

为增强算法面对异常值时的鲁棒性，本文采用基于ℓ2，1范数的损失函数来去除异常值，而不使用对异常值敏感的ℓ2范数损失函数。以最小二乘回归为例，使用ℓ2，1鲁棒损失函数后目标函数如式（19）所示：

其中：γ为正则化项参数；W∈RM×C。

将上述目标函数变为带约束的形式，如式（20）所示：

将上述的问题改写为：

使A=[XTγH]，B=，其中H∈RN×N为单位矩阵，则目标函数进一步改写成式（22）：

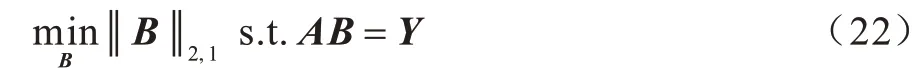
RFS 使用一个非常简单的方法来求解式（22），同时这种方法也很容易应用到其他一般的ℓ2，1范数最小化问题中。

该算法主要基于拉格朗日方法，构造拉格朗日函数如下：

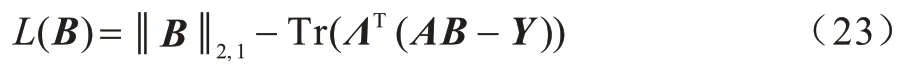
求上式对B的偏导并令其为0，得到式（24）：

其中：D是对角矩阵。

第n个元素为：

在式（24）两边同乘AD-1，并有AB=Y，得式（26）：

将式（26）代入式（24），得：

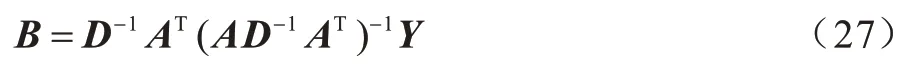
由于式（22）中的问题是一个凸问题，当且仅当满足式（27）时，B是该问题的全局最优解。其中，D依赖于B，因此也是一个未知变量。依然使用迭代算法来获得满足式（27）的解B：在每次迭代中，用当前的D计算B，然后根据当前计算的B更新D。不断重复迭代过程，直到算法收敛。具体描述如算法1所示。

2.2 算法分析

本文提出的算法在每次迭代计算中都单调地减少式（22）中问题的目标。

引入以下引理对其进行证明：

引理1对于任意非零向量b，bt∈Rc，以下不等式成立：

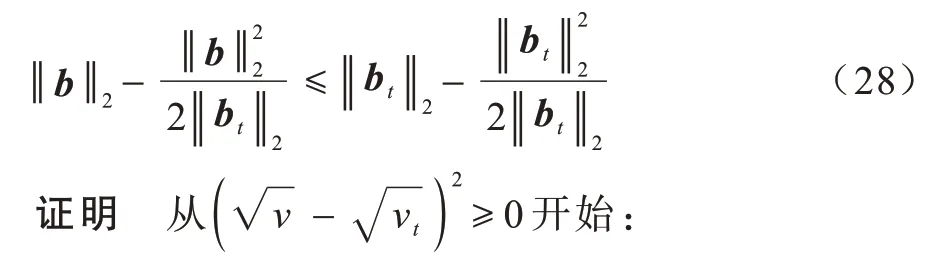
算法的收敛性总结为以下定理：

将式（29）中的v和vt分别带入，可以得到式（28）。

定理1算法每次迭代都会单调地降低式（22）中问题的目标，并收敛于问题的全局最优。

证明可以验证式（27）是以下问题的解：

因此在t次迭代中：

这表明：

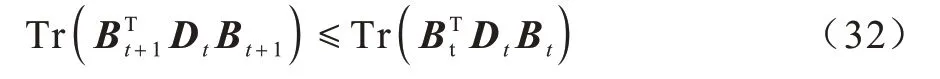
即：

根据引理1，对每个i有：

因此，以下不等式成立：

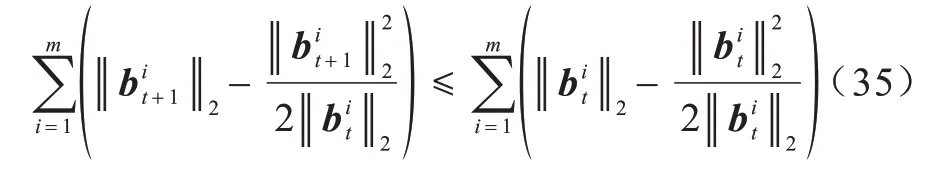
结合式（33）和式（35）可以得到：

即：

因此，本文提出的算法在每次迭代中将单调地降低式（22）中问题的目标。在收敛性上，Bt和Dt满足式（27），又因为式（22）是一个凸问题，所以满足等式（27）表示B是式（22）的全局最优解，因此，算法将收敛于问题式（22）的全局最优。

3 实验与结果分析

为了检验所提算法的有效性，本节分别在合成数据集和真实数据集上进行实验，在不完整数据集中比较了本文提出的PMF、SID 算法、传统的先填充再进行特征选择算法，其中传统方法中的填充算法分别为概述中介绍的均值填充（mean）、KNN 填充、EM 填充，特征选择算法为本文使用的鲁棒特征选择算法RFS 和两种基于边缘的特征选择算法：Simba［19］和Relief［20］，分别将以上几种算法交叉组合形成9 套完整的针对不完整数据集进行特征选择的流程，以评估本文所提算法在高维数据上的分类性能。

本节使用分类精度（ACC）作为评估指标。ACC表示样本分类正确的百分比，即：

其中：N是样本总数；Nc为正确被分类的样本个数。

3.1 实验设置

本实验环境为MATLAB2019a，为了观察缺失率对算法的影响，本节人工随机地向数据集注入不同比例的缺失值。缺失率范围为5%～65%，以10%为间隔递增，本文缺失率定义为缺失值占所有值的百分比。在此仅考虑缺失机制为完全随机缺失的情况。为了体现特征选择算法的效果，具体地，本文会向特征较少的数据集中添加一些无关特征，实验中向数据中添加的无关特征并不被注入缺失。

如前所述，K为矩阵U和V的维度，当其取不同值时均方根误差的收敛速度如图1 所示，这里分别取K=1，5，10，15，20，可以看到：当K=1，5 时收敛速度较慢并且无法收敛到0，当K=10，15，20 时均方根误差收敛较快，并且可以收敛到0，可见，K的取值不光影响均方根误差收敛速度，还会影响最终收敛结果。为了不增加计算量并且防止过拟合，本文所有实验均设置K值取10。

图1 不同K 值时均方根误差随迭代次数的变化Fig.1 Variation of root mean square error with iteration times at different K values

不止K的取值，学习速率α的取值不同也会影响均方根误差的收敛速度，如图2 所示，α分别取0.1、0.01、0.001、0.000 1，由图2 可见，α取0.01 时收敛速度最快，α取0.000 1 时收敛速度最慢，可见步长越小，损失函数到达底部的时间越长，步长越大，损失函数收敛越快，但步长并不能无限大，经过实验发现当α取0.1 时，目标函数不会收敛，所以在该合成数据集上α取0.01。经过在不同数据集上的实验也发现，同一个步长并不适用于所有数据集，所以要通过多次实验发现最适合本数据集的步长，本文中所有数据集步长设置均经过多次实验，设其为最恰当的数值。

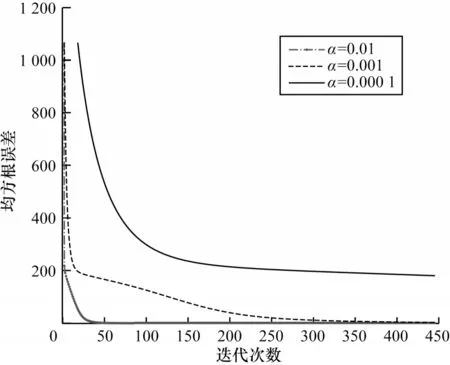
图2 不同α 值均方根误差随迭代次数变化Fig.2 Variation of root mean square error with iteration times at different α values

3.2 数据集合成

本节通过设计合成数据集来评价本文算法在存在大量不相关变量的不完整数据中填充缺失值后选择出相关特征的能力。合成数据集包含500 个实例和100 维特征。其中两维特征是随机产生的0、1 序列，将这两维特征做异或运算，产生结果即为合成数据集的标签，剩下的98 个特征服从于以0 为均值、1为方差的标准正态分布。

本节以所选择的无关特征数目为标准评价特征选择方法。为了简便期间，只比较本文提出的算法与SID 算法，以及使用LBFS 算法作为特征选择算法的3 种传统方法，实验结果如图3 所示。

图3 无关特征数随缺失率的变化Fig.3 Variation of irrelevant feature number with deletion rate

由图3 可以看出，在该数据集上，KNN 填充的方法选择出的无关特征数目最多，效果最差，本文提出的算法PMF 效果最好，在缺失比例较高的情况下依然能选择出较少的无关特征。SID 算法在缺失率较低的情况下效果较好，但在缺失率较高时不如PMF。

3.3 真实数据集

本节分别从LIBSVM 数据网站、UCI website［21］、肯特岗生物医学数据集等网站下载DLBCL、Mnist、Splice、Wpbc、USPS、Arcene 6 个真实数据集。由于生物医学方面数据集往往包含大量冗余特征，更能体现出特征选择的作用，本节选用的数据集大部分与生物医学有关。DLBCL 为弥漫大B 细胞淋巴瘤基因的相关数据集，Splice 是关于识别DNA 序列中两种类型的剪接点的数据集，Wpbc 数据集则取自威斯康辛大学校医院的乳腺癌病例数据库，Arcene 原始数据来自于美国国家癌症研究中心和东维多利亚医学院，收集了通过SELDI 技术采集的癌症病人和健康人的质谱信息，用于癌症预测。由于Splice 和Wpbc 数据集特征较少，这里人为的向其添加2 000 个无关特征，无关特征的特征值均通过从正态分布N（0，1）中抽样得到。数据集详细信息如表1所示。

表1 数据集详细信息Table 1 Datasets detailed information

对于真实数据集，因为无法预知其中特征的重要性，所以使用分类准确率为标准评价特征选择方法。在训练集上先进行特征选择，之后对所选特征进行分类，分类准确率高说明特征选择的效果越好。

使用交叉验证方式［22］选择最佳参数组合，将原始数据集分为70%的训练集和30%的测试集，其中训练集的类标签是已知的，假设测试集的类标签未知，通过在训练集上训练得到分类器来预测测试实例的类标签，比较预测得到的类标签与真实的类标签就可以得到该分类器的分类精度。本实验使用SVM 分类器进行训练。对于基于KNN 填充进行的特征选择，本文选取k=5。

各算法在DLBCL 数据集上的分类效果柱状图如图4 所示，其中纵坐标为分类准确率，横坐标依次展示11 种不同的算法，不同底纹代表不同的缺失率，这里选取了缺失率为25%、35%和55%时的分类结果，可以看到，本文提出的算法在不同缺失率时准确率都高于其他10 个算法，均值填充的3 种算法在该数据集上的整体表现略高于KNN 填充和EM 填充，并且3 种不同的特征选择算法效果相差不大，SID算法效果仅次于PMF，因为其利用了不完整数据集中的全部信息，但该算法没有考虑异常值的影响。

图4 不同缺失率下DLBCL 数据集的分类准确率Fig.4 Classification accuracy of DLBCL dataset under different miss rates

各算法在Mnist 数据集上的分类效果如图5 所示，可以看到，在缺失率较高的情况下，本文提出的算法依然能达到90%的准确率，在该数据集中用KNN 填充的3 种算法效果较差，可能是该数据集比较稀疏导致近邻关系度量不够准确，EM 填充与SID算法效果相差不大，略高于均值填充。

图5 不同缺失率下Mnist 数据集的分类准确率Fig.5 Classification accuracy of Mnist dataset under different miss rates

各算法在Splice 数据集上的分类效果柱状图如图6 所示，可以看到，基于KNN 填充的算法效果较差，在缺失率为25%时只可以达到70%左右的准确率，PMF 在相同缺失率时可以达到80%以上的准确率，可见PMF 在该数据集上效果有了较大的提升。基于均值填充的算法和SID 算法效果较为接近。

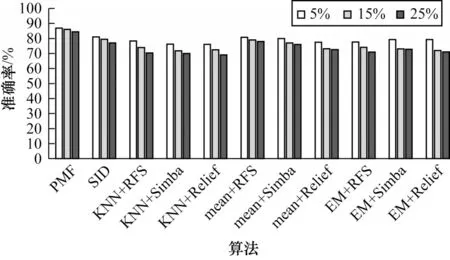
图6 不同缺失率下Splice 数据集的分类准确率Fig.6 Classification accuracy of Splice dataset under different miss rates

各算法在Wpbc 数据集上的分类效果柱状图如图7 所示，可以看到，在该数据集上各个算法的分类准确率普遍较低。在该数据集上基于KNN 填充的算法效果较差，均值填充在25%缺失率时的效果较好，在KNN 填充和均值填充上RFS 特征选择算法的效果比Simba 和Relief 略高。相比其他算法，本文提出的算法在该数据集上效果依然是最好的。

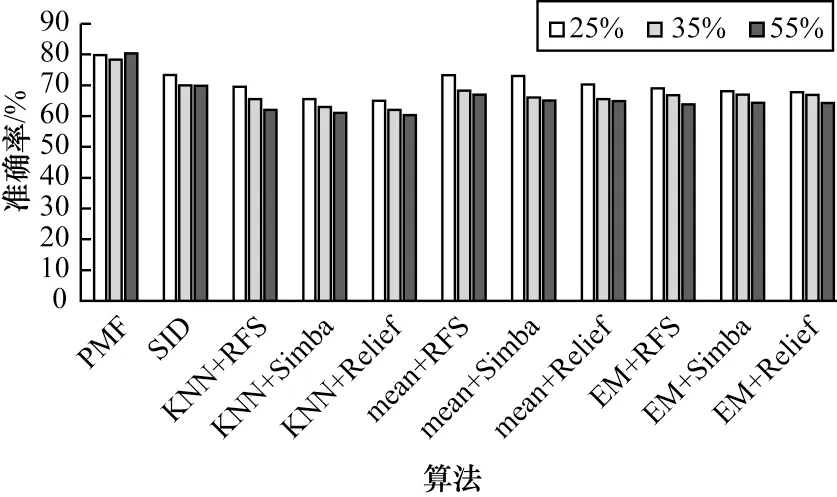
图7 不同缺失率下Wpbc 数据集的分类准确率Fig.7 Classification accuracy of Wpbc dataset under different miss rates

各算法在USPS 数据集上的分类效果柱状图如图8 所示，可以看到，本文提出的算法在该数据集上效果较好。在缺失率为5%时，所有算法的分类准确率都高达92%左右，但是随着缺失率增大到55%，其他算法的分类效果有了明显下降，此时本文提出的算法优势更加明显。相比之前的基于填充的算法，SID 算法在该数据集上并不具有明显的优势。

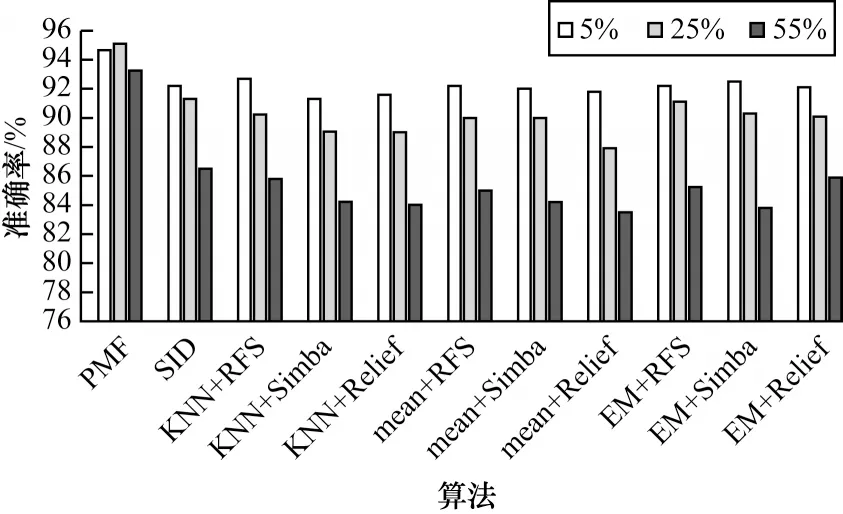
图8 不同缺失率下USPS 数据集的分类准确率Fig.8 Classification accuracy of USPS dataset under different miss rates

各算法在Arcene 数据集上的分类效果如图9 所示，可以看到，本文提出的算法在该数据集上的优势非常明显，其他10 种算法在所有缺失比例时的准确率基本都在60%左右，然而PMF 算法可以达到90%左右的准确率，可见本文提出的算法非常适用于该数据集，这应该与数据集本身有关。

图9 不同缺失率下Arcene 数据集的分类准确率Fig.9 Classification accuracy of Arcene dataset under different miss rates

3.4 异常值检测

本节使用3.2 节中的合成数据集进行异常值检测，为了方便展示，人工随机地向数据集注入不同比例的异常值，这里使用固定值来模拟异常值。分别在异常值比率为1%、2%、3%时进行实验求无关特征，异常值比率定义为注入异常值的数量占整个数据集的百分比，结果如表2 所示，本文固定缺失值比率为5%。从表2 的数据可以看出，在异常值比例较低时，本算法能筛选出所有的重要特征，随着异常值比率增加，筛选出的无关特征数目有所增加，但仍然保持较低的数量，可见本文算法可以在一定程度上应对不完整数据集中异常值带来的影响。

表2 不同比例异常值与无关特征数目Table 2 Different proportion outliers and irrelevant features number

综上所述，基于KNN 填充算法在Mnist 和Splice数据集上效果较差，虽然该算法利用样本近邻关系来进行填充，在一定程度上更多地利用了不完整数据集的信息，但是近邻关系度量的准确性也会对填充效果造成影响。基于均值填充算法与EM 填充算法效果略高于KNN 填充算法、SID 算法效果仅次于本文算法，因为该算法使用指示矩阵利用了不完整数据集中的全部信息，但是它没有考虑数据集中异常值的影响。PMF 算法效果最好，因为其不仅充分利用了不完整数据集中的所有有效信息，还使用ℓ2，1范数作为损失函数，增强了其应对异常值的鲁棒性，所以与其他算法相比，在所有数据集上分类准确率都有所提升。

4 结束语

高维数据集中通常包含缺失值和离群值，对其进行降维是数据挖掘的重要步骤之一。本文针对不完整数据中含有未被观察信息和存在异常值的特点，提出一种基于概率矩阵分解技术的鲁棒特征选择方法。该方法引入指示矩阵利用数据集中全部信息，对不完整数据集进行近似估计，在考虑异常值情形下，利用ℓ2，1范数对数据点中异常值具有鲁棒性的特点，将其作为回归损失函数，实现鲁棒特征选择。实验结果表明，该方法能够充分利用不完整数据集中的所有信息，避免繁琐的距离运算，可有效应对不完整数据集中异常值带来的影响。下一步考虑将概率矩阵分解填充拓宽到半监督或无监督的特征选择流程上，在数据集标签有缺失甚至无标签的情况下，提升特征选择的效果。