ZUC‑256 流密码轻量级硬件设计与实现

李 沐，崔益军，倪子颖，王成华，刘伟强

（1.北京卫星信息工程研究所，北京 100086；2.南京航空航天大学电子信息工程学院/集成电路学院，南京 211106）

引 言

流密码是一种对称性的密码算法［1］，它可以很容易地在硬件中实现并且得到很高的性能。由于流密码在加密和解密过程中速度快，并且在传播过程中误差小，所以经常被用于无线通信。ZUC⁃128［2］和ZUC⁃256［3］都是流密码。ZUC⁃128 算法能够提供128 位的安全性，但由于下一代5G 通信和量子化的发展，ZUC⁃128 在不久的将来将无法满足要求。基于以上原因，作为ZUC⁃128 的升级版本，ZUC⁃256 算法于2018 年被提出。ZUC⁃256 算法一共包括2 个子算法，分别是ZUC 流密码（ZUC）和完整性算法（EIA3）［3］。ZUC⁃256 算法的输入来自1 个256 位的密钥和1 个184 位的初始向量，在输出阶段每个周期输出1 个32 位的流密码。EIA3 算法基于ZUC 流密码产生的结果，可以通过判断信息的每1 个比特来计算出1 个Tag 结果。

目前关于ZUC⁃256 硬件实现的研究较少，而对于ZUC⁃128 的硬件设计已经有了大量的研究，对于ZUC⁃256 的硬件设计具有一定参考价值。Wang 等［4］在2011 年提出了3 种不同的优化架构来实现ZUC⁃128，并且比较了这3 种架构的整体性和复杂性；在2012 年提出一种高吞吐率的结构［5］，但其会消耗较多资源。2016 年，一个基于ZUC⁃128 的机密性算法（EEA3）架构被提出［6］。2020 年Wang 等［7］提出一种五级流水的ZUC⁃256 流密码实现方案，其吞吐率达到了3.687 Gb/s。由于ZUC 算法主要用于通信传输信息的加密，因此常用于资源受限设备，所以对于ZUC 算法的低资源设计尤为关键。基于此，本文基于FPGA（Xilinx Kintex⁃7）架构设计并实现了2 种ZUC⁃256 的流密码结构和1 种EIA3 算法结构。

1 ZUC‑256 流密码算法和EIA3 算法

1.1 ZUC‑256 流密码

ZUC⁃256 流密码算法［3］包括3 个逻辑层次：线性反馈移位寄存器（Linear feedback shift register，LF⁃SR）、位重组（Bit recombination，BR）和有限状态自动机（Finite state machine，FSM），记 为F。ZUC⁃256 流密码将1 个256 位的原始密匙K和1 个184 位的初始向量IV作为输入，并在每个循环内输出32 位密码。

LFSR 层有16 个31 位的向量（s0，s1，…，s15），并包含2 个阶段，分别为初始化阶段和工作阶段。在初始化阶段，LFSR 层的每个向量是由位常数D、256 位初始密钥K和184 位初始向量IV组成。然后，LFSR 通过将s15、s13、s10、s4、s0合并计算，得到的结果与F层中的1 个31 位输入u相加得到新的s0。u是通过将W向右移动1 位得到，而W来自于有限状态自动机F。在16 个向量向右移动后，s15得到1 个新的数值。工作阶段与初始化阶段的区别是在工作阶段时W将被设置为0。

BR 层使用8 个31 位来 自与LFSR 层的向量来计 算出4 个32 位 的数据，分别为X0、X1、X2和X3。在ZUC⁃256 中，选取s0、s2、s5、s7、s9、s11、s14、s15作为输入，生成的4 个结果分别满足：X0=s15H||s14L；X1=s11L||s9H；X2=s7L||s5H和X3=s2L||s0H。

有限状态自动机F包含2 个存储单元R1和R2，分别来自于BR 层的输出X0、X1、X2和X3，并且由这2个存储单元来生成新的W值。存储单元的初始值均设置为0。在FSM 层中，需要通过加法、异或和S⁃box 运算得到结果。在ZUC⁃256 中，S⁃box 的值与ZUC⁃128 相比没有发生变化，依旧使用2 个不同的S⁃box，每个S⁃box 使用2 次。

ZUC⁃256 流密码在工作状态下的结构图如图1 所示。图中S表示S⁃box 的值，L1、L2表示异或运算。ZUC⁃256 流密码每次运算需要进行32 轮的初始化运算，前32 轮的计算使用W移位1 位得到新的16 个向量组合来产生新的s15向量，然后将LFSR 层中的16 个向量逐一向右移动。在第33 轮中执行与前32轮相同的操作但是此时W的值应被设置为0。之后，每一轮的运算都可以连续产生32 位流密码结果。ZUC 算法在初始化阶段不输出结果。

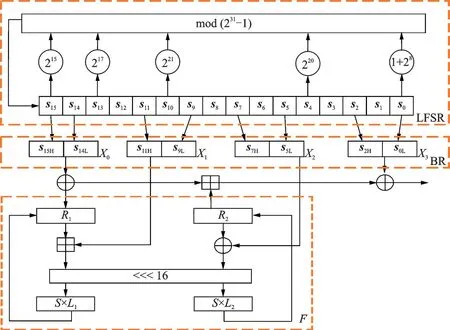
图1 ZUC⁃256 流密码的工作阶段Fig.1 Work stage of ZUC⁃256 stream cipher

1.2 EIA3 算法

EIA3 算法使用通用哈希算法原理生成Tag 标签值。如同任何其他形式的哈希算法加密，EIA3 算法可以将任意长度的信息转化为指定长度的标签值，信息的微小变化会导致Tag 标签值发生显著变化，常用于数字签名中。

在EIA3 算法中，根据信息中的每个比特值对Tag 值进行迭代。对于ZUC⁃256 的EIA3 算法来说，如果当前信息的值为‘1’，那么新的Tag 值就是旧的Tag 值和32 位流密码的异或结果，且用于计算的32位流密码每次只向右移动1 位。当信息检索完成后，ZUC⁃256 流密码再向右移动1 位，并且执行同样的操作。在ZUC⁃256 中，Tag 值的长度一共有3 个版本，分别为32 位、64 位和128 位。Tag 的初始值被定义为32 位流密码的第1 组，设置信息M的长度为L。EIA 算法过程如算法1 所示。

算法1EIA3 算法

2 两种ZUC‑256 流密码和EIA3 算法硬件结构

2.1 ZUC‑256 流密码硬件结构

本文研究目的是在硬件上对ZUC⁃256 流密码进行高性能实现。在ZUC⁃256 的结构中，整体结构运行的主要时延来自于LFSR 层中的7 个数相加取模运算。对于BR 层来说，因为只需要改变LFSR 层向量的位置，基本上不会产生很大的关键路径延时。有限状态机的FSM 计算来自于加法运算、异或运算和S⁃box 检索替换操作，所以F层的电路延迟比LFSR 层小得多。因此，本设计的关键路径延迟是在LFSR 层，为了实现ZUC⁃256 的高性能设计，应该减少这部分延迟。

ZUC 算法中的LFSR 层中包含2 个阶段，分别为初始化阶段和工作阶段。在初始化阶段，LFSR 层需要计算

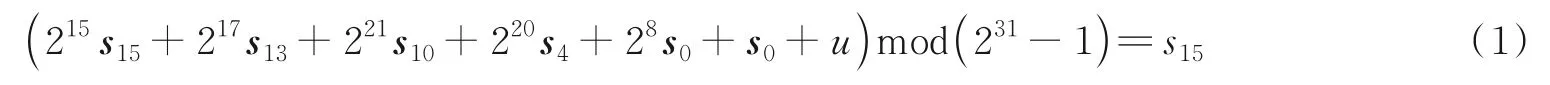
对于式（1），可以看成计算多次(A+B)mod(231-1)，其中A、B表示2 个31 位输入数据。针对2 个数的相加取模，图2 中的2 种加法器均可以完成以上操作。对于串行模加结构，一共使用2 个31 位加法器，第1 个加法器对输入数据进行加法操作，第2 个加法器对第1 步得到的进位和加法和进行相加，得到模约减后的结果。该结构一共使用了2 个加法器，关键路径同样是来自于2 个级联的加法器。对于并行模加结构，同样使用了2 个加法器，分别计算A+B和A+B+1，再通过A+B的加法器中产生的进位来选择最终加法结果。相较于串行模加结构，该加法器同样使用了2个加法器，但是第2 个加法器的输入为3 个，这会造成该次加法的关键路径增加，但是由于加法器是并行结构，关键路径显著少于串行模加结构。基于以上2 种不同的加法器，本文设计了2 种ZUC⁃256 流密码的结构。

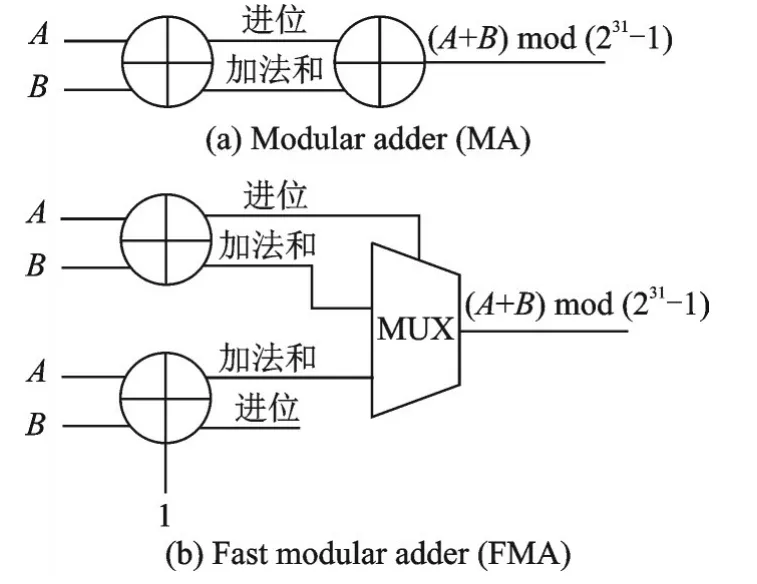
图2 ZUC⁃256 中使用的2 种加法器Fig.2 Two different adders used in ZUC⁃256

2.1.1 ZUC⁃256 结构1

在LFSR 层的初始化阶段，一共需要对7 个数字进行加法操作，而在工作阶段则需要加6 个数字。因此，如果直接使用MA 和FMA 加法器，产生的电路关键路径延迟将不可忽略。但是对于多个数据相加，只需要在最后阶段计算出精确的数值，在中间阶段只需要尽量减少数据相加带来的关键路径延时即可。进位保存加法器（Carry save adder，CSA）是一种关键路径延时很小，并且可以将多个数据组合相加的加法器，同样该加法器无法得到最终的加法和。该加法器的原理是，进位和加法和的每1 位都是独立产生的，当加法器的位数增加后，对于关键路径没有任何影响，只会增加加法器的资源面积，每次加法产生结果只需要几个门的延时，并且生成3 个数据相加的进位和加法和。当输入的数据为3 个时，将1 个CSA 加法器和1 个普通加法器级联可以快速得到3 个数据的加法结果。

使用这样级联的加法器可以快速完成7 个输入数据的加法操作。在本设计中一共使用了包含CSA 加法器的2 层级联结构，在每1 层中输入输出的长度被扩大4 位。当所有的加法都完成后，再使用串行模加结构对数据进行模约减操作。由于进位和加法和的结果小于231，该结构只需要进行一次模约减操作。

ZUC⁃256 结构1 的LFSR 层结构如图3 所示，其中A～F分别表示31 位输入数据。该结构中每轮计算一共使用3 个时钟周期：在第1 个时钟周期中除了u=W≪1 以外的6 个数字将被相加，同时计算出u。在第2 个时钟周期中将第1 步得到的6 个数据相加的结果再与u相加；在第3 个周期中对16 个寄存器中的数据进行移位操作，最后得到新的s15值。对于FSM 层，需要进行加法、异或和S⁃box 等操作。与BR 层相比，FSM 层的电路延迟较大。由于LFSR 层在每个迭代中使用3 个时钟，因此可以将F层的计算分解成3 个时钟来完成。

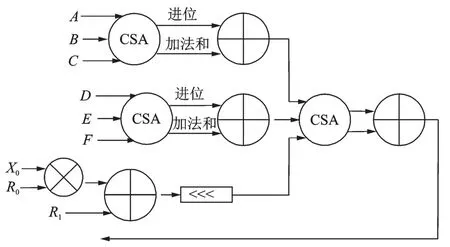
图3 ZUC⁃256 结构1 中LFSR 层结构Fig.3 LFSR layer architecture of ZUC⁃256 Structure 1

当电路运行在工作阶段时，由于生成的密钥在每4 个周期内只产生1 次，在第1 个周期和最后2 个时钟周期中会产生不需要的值。因此，需要在第2 和第3 个时钟周期设置1 个信号，以确保在计算EIA3 算法时可以使用准确的密钥。

2.1.2 ZUC⁃256 结构2

在ZUC⁃256 结构1 的设计中，如果每个CSA 加法器的进位和加法和并不完全计算出来，等到最后时刻再计算，那么电路的关键路径将会极大减少。受文献［7］启发，本文设计了ZUC⁃256 结构2，使用多个CSA 加法器级联，并且由于单个CSA 加法器的关键路径很低，在同一个周期中计算多个级联CSA 加法器。

ZUC⁃256 结构2 的LFSR 层结构如图4 所示。在第1 层中，该结构使用2 个CSA 加法器对于6 个数据同时进行加法操作，这样产生了2 个进位和2 个加法和。对于前一级中CSA 加法器产生的进位在后级中进行加法操作，需要将进位值向左移动1 位。当6 个数值的加法计算结束之后，首先将最后一级CSA 加法器中的进位和加法和相加。这里的加法操作使用1 次并行模加结构的加法器，因此得到的结果就是模约减后的结果。

图4 ZUC-256 结构2 中LFSR 层结构Fig.4 LFSR layer architecture of ZUC-256 Structure 2

由于本文设计目的是通过达到更高的频率来提高ZUC⁃256 流密码的吞吐率，因此对于电路结构的设计思路是在初始化阶段将LFSR 层的计算分割成3 个周期，但是在工作阶段由于W不参与计算，将其分割成2 个周期。在初始化阶段，用第1 个周期来计算3 层级联的4 个CSA 加法器和u；在第2 个周期中，使用1 个并行模加加法器来计算6 个输入数据之和的模约减；在第3 个周期中，同样再使用1 次并行模加加法器，并得到最终结果。在工作阶段，W值不再参与运算，此时只需要计算6 个数字的总和，当第1 个并行模加加法器计算完成后，这个结果便是最终结果。同样地，由于LFSR 层的周期减少，使得该结构不能使用3 个周期内计算BR 层和FSM 层。幸运的是，这2 层的电路延迟很小，可以在2 个周期内完成并且不影响整体运行的频率。对于这2 层，在第1 个周期计算w1=（R1+X1）mod 232和w2=（R2+X2）mod（231-1），然后重新组合，最后进行线性变换；在第2 个周期中，该结构只进行S⁃box 操作。

2.2 EIA3 算法的硬件实现

EIA3 算法的Tag 值是基于ZUC⁃256 流密码算法进行计算，并且相较于ZUC⁃128 中的算法做出了较大改动。在本文设计中，EIA3 的输出使用64 位的Tag 值。由于流密码每轮输出32 位，Tag 值的加载需要2 个周期。从算法1 可以看出，如果Tag 的长度为64 位，Tag 的第1 次计算将从第64 位开始。所以该结构需要在第5 个周期计算Tag 值。由于Tag 值的计算在每个迭代中只移动1 位，这样在每个周期中只计算一次会拖慢运算速度，因此本文设计中单个周期可以对32 位的信息进行处理。

因为流密码每次产生32 位，而Tag 值的长度是64位，在该结构中使用1 个96 位的寄存器来保存连续3个周期中产生的各32 位流密码。每当产生1 个新的32 位流密码时，将该流密码的值从96 位寄存器的低32位处输入，同时将该寄存器的高32 位输出抛弃。如图5 所示，每个信息被设计成1 个选择器，图中W0～Wi均表示64 位寄存器。如果信息的i位为0，Wi寄存器将被设置为0；如果信息的i位为1，Wi寄存器将被设置为本周期内96 位寄存器右移i位的最后32 位。这样1个时钟周期可以并行处理32 位消息，可以节省大量的计算时间。

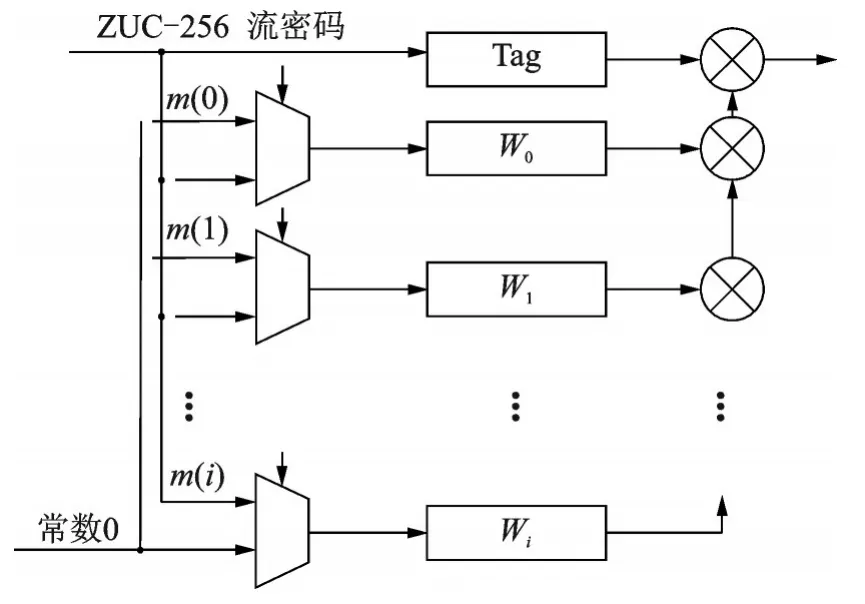
图5 EIA3 算法的硬件结构Fig.5 Hardware structure of EIA3 algorithm

需要注意的是，当最后一组信息进入该结构时，需要在信息的最后1 位加上1 个比特“1”，然后通过上述方法得到最终的迭代结果。最后，通过计算Tag初始值和最后的迭代结果来得到最终的Tag 值。

3 ZUC‑256 流密码硬件实现与性能对比

本节使用FPGA 对于ZUC⁃256 的2 种结构和基于ZUC⁃256 的EIA3 算法结构进行实现。所有设计均使用Vivado 2020.1 进行综合，并且在Kintex⁃7 FPGA 平台上进行实现，然后通过后仿真对其性能进行对比。由于ZUC⁃256 相关的硬件设计结果较少，在本文中引入部分关于ZUC⁃256 的软件设计结果进行对比。为了公平起见，对于ZUC⁃256 流密码的设计，资源部分不包含EIA3 算法资源。图6 是包含EIA3 计算的完整实现仿真图。图6 中最开始进行ZUC 的31 轮初始化运算，之后产生连续的32 位ZUC流密码。当第1 个流密码产生后，多Tag 进行初始化，然后单次对32 位信息进行处理，最终得到Tag结果。

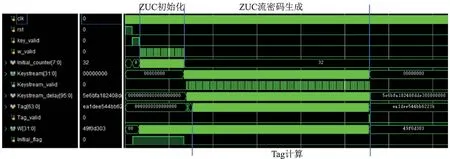
图6 ZUC⁃256 FPGA 实现仿真时序图Fig.6 Simulation timing diagram of ZUC⁃256 implementation on FPGA

本文的ZUC⁃256 硬件实现与对比结果如表1 所示。由表1 可见，结构1 可以达到更高的频率，并且使用了更少的资源，但是由于其在4 个周期中才会产生1 次有效的结果，因此吞吐率只有4.78 Gb/s。而对于结构2 来说，由于改进了其流水线结构，使用了更短的流水线，尽管在频率上不及结构1，但却获得更高的吞吐率，达到6.72 Gb/s。与现有其他ZUC⁃256 的硬件设计相比，本文ZUC⁃256 结构2 吞吐率提升了45.24%。与其他基于RISC⁃V 平台的ZUC⁃256 结构相比，本文结构在吞吐率方面也有显著提升。

表1 本文ZUC‑256 结构与其他ZUC‑256 结构性能对比Table 1 Performance comparison of designed and previous ZUC‑256 structures

此外，本文还将ZUC⁃256 的设计结果与ZUC⁃128 设计结果进行对比，如表2 所示。从表2 中可以看出，本文设计的结构达到了更高的运行频率。这是因为本文结构分割了更多的流水线，使得整体结构上的关键路径减少。并且由于频率的提高，尽管本文设计的结构使用了更多的周期，但是吞吐率仅略低于文献［8］的ZUC⁃128 结构。同时本文结构使用了更少的资源，因此在吞吐率/面积方面相较于文献［4，8］的ZUC⁃128 结构分别提升了43.58%和54.95%。对于ZUC⁃256 结构1，在资源上相较于文献［4，8］的ZUC⁃128 结构分别减少38.48%和61.91%。

表2 本文ZUC‑256 结构与其他ZUC‑128 结构性能对比Table 2 Performance comparison of designed ZUC‑256 structures and previous ZUC‑128 structures

本文设计的EIA3 算法硬件实现主要使用了ZUC⁃256 结构1 产生的ZUC⁃256 流密码，算法性能如表3 所示，其中Tag 位宽均为64 位。从表3 可以看出，基于ZUC⁃256 的EIA3 算法结构在资源上相较于单独的ZUC⁃256 结构2 仅增加37 个Slice 块，运行频率与ZUC⁃256 结构1 保持一致。此外，该结构使用流水线设计，一次性可以处理32 位数据，对1 次128 位数据生成64 位签名只需要0.71 μs。

表3 基于ZUC‑256 的EIA3 算法的硬件实现及其性能Table 3 Hardware implementation of EIA3 algorithm based on ZUC‑256 and its performance

4 结束语

本文设计了2 种不同流水线的ZUC⁃256 硬件实现电路：第1 种结构使用三级流水线，使用了更少的资源，达到了更高的频率；第2 种结构使用两级流水线，可以达到更大的吞吐率。与目前最快的ZUC⁃256 流密码硬件设计相比，第2 种设计在吞吐率上提升54.95%。本文还设计了一种基于ZUC⁃256的EIA3 算法的硬件结构，仅仅使用37 个Slice 块的资源，对1 次128 位数据生成64 位签名只需要0.71 μs。本文设计的ZUC⁃256 结构使用了更少的资源，因此更加适合于资源受限的场合。未来的工作将着眼于ZUC⁃256 在资源受限情况下的更高性能设计。