基于APDL 的缆车架参数化建模与仿真

王 骏， 韦 磊

（中国船舶重工集团公司第七二三研究所， 江苏 扬州 225000）

0 引言

缆车是城市、山地风景游览区常用的交通运输工具，它通过钢丝绳牵引，将乘客和货物运输到特定的目的地[1-3]。缆车的工作原理是驱动机驱动钢丝绳， 从而带动固定在钢丝绳上的缆车车厢循环运动， 实现了乘客和货物的连续运输。缆车由于装备位置和环境的特殊性，需要满足室外高空的工作条件，且需要承受风雪等极端载荷，其安全性至关重要。 缆车内部的主要结构部件缆车架承载缆车和乘客的全部重量，因此需要对其结构强度进行校核。

在实际的工程应用中， 往往需要将具体工程问题抽象为能够解决的等效模型， 列出相应的基本方程和边界条件， 才能够通过经典的弹性或者塑性力学的求解方法获得解析解。但是大多数情况下，实际的工程问题都会出现研究对象形状不规则、 载荷和边界约束条件复杂不单一， 因此很难获得相应的解析解。 为了解决复杂工程问题，人们提出了多种不同的数值解法，具体包括有限单元法、边界元法、离散元法和有限差分法等，即不需要求解出解析解，可以得到精确的数值解。由于有限元法研究较为深入，已经具有很强的理论应用基础和软件应用基础，因此广泛应用于工程实际问题的解决之中。

由于缆车架内部型材具有不规则的横截面， 且缆车架内部空间布置结构复杂，常规的理论计算难以对缆车架进行准确的力学分析， 本文通过有限元软件ANSYS 进行缆车架的参数化建模与分析[4-7]，一方面提高了计算效率，另一方面能够方便地对缆车架进行进一步的设计优化。

1 缆车架受力分析

1.1 缆车架机械结构

缆车架的机械结构组成图见图1， 主要包括顶梁、上边梁、立柱、下边梁、底梁、上框、门梁和下框。 其中顶梁、上边梁、下边梁、底梁、门梁和立柱均为弧形结构，顶梁、上边梁、下边梁、底梁分别有四根， 首尾与分别四根立柱相连， 且呈矩形状由上而下平行布置。 上框固定在四根上边梁内侧， 下框固定在四根下边梁内侧， 两根门梁固定在上边梁和下边梁之间。

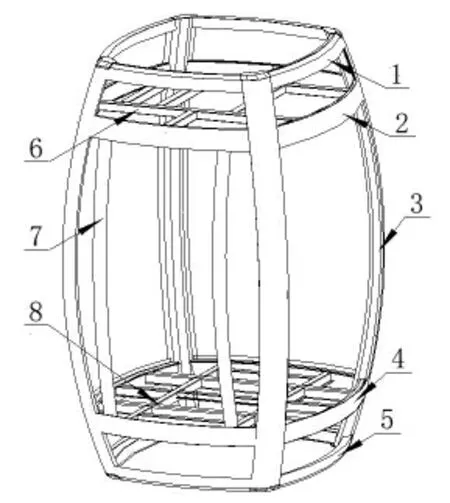
图1 缆车架机械结构组成图

缆车架是缆车的主要承载部件， 需要承受缆车自身的玻璃围挡、门和空调等设备的重量，缆车内部乘客的重量，以及缆车外部的冰雪载荷、风载，受力情况较为复杂，因此需要进行力学分析， 计算其在满载极限条件下的受力情况，方便对其安全性进行合理的评估。

1.2 缆车架极限载荷计算

为了确定缆车架的结构强度能否满足要求，需要先计算出缆车架的受力情况，图2 为缆车结构外形图，基本外形尺寸为2000mm×1900mm×2800mm， 自重为Gk=4900N，额定载荷为Gy=700N/人×6 人=4200N，运载总载荷P1=Gk+Gy=9100N。 缆车所受的风压为

图2 缆车结构外形图

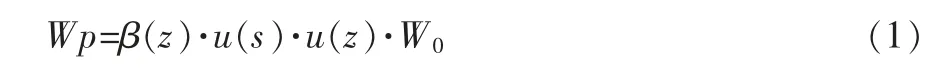
式中：β（z）—风振系数，工作状态取2.462，非工作状态取2.636；u（s）—体型系数，此处取1；u（z）—风压高度变化系数，此处取2；W0=v2/1.6，v—风速。极限状态下，W0=450Pa，Wp=2.636×1×2×450=2372Pa， 风载荷F=Wp·A=2372×5.1=12100N。 缆车顶部的冰雪载荷压力为0.35kN/m2，缆车上顶面积为2m2，冰雪载荷Q= 0.35×2=0.7kN。门两侧玻璃的重量为287N，门对面玻璃的重量为250N，门上玻璃的重量为56N。

缆车架通过顶部四个顶点与主轴的结构件固定，因此可以等效为对缆车架四个顶点施加完全约束， 缆车架的结构强度和位移变形能否满足要求需要通过ANSYS 软件进一步验证。

2 缆车架APDL 仿真

2.1 APDL 有限元模型建立

ANSYS 有限元分析软件是一款功能十分强大的大型分析计算软件， 可以广泛应用于交互式的多学科研究中。 ANSYS 软件不但可以用于机械、军工、电力、建筑等各种不同的学科， 而且在各个不同的学科中均能够发挥其强大的分析计算功能。随着软件的广泛应用，内部求解算法一步步更新优化，功能界面也越来越人性化。在机械领域，ANSYS 软件可以在不生产加工样机的前提下，进行前期的建模、仿真、计算与分析，一方面节约了大量的工程制造成本，另一方面缩短了研发周期，保证了时间节点。 ANSYS 有限元软件可以进行线弹性静力学分析、非线性分析、热分析、动力学分析等多种不同的分析类型，且可以应用于不同学科交叉的耦合分析。 本文缆车架具有复杂的机械结构和截面形式， 常规的理论计算难以推导出准确的力学计算公式，因此借助于ANSYS 软件进行仿真求解。

APDL 的全称是ANSYS 参数化设计语言， 通过软件自带的程序语言，编写命令流程序，能够实现ANSYS 界面下的参数化建模、参数化定义单元和材料、参数化划分网格、参数化定义载荷、参数化设置求解类型求解以及参数化后处理。在建模和划分网格的过程中，往往需要进行模型的修改和网格密度的调整，APDL 语言能够方便地对各种参数进行修改， 极大地减少重复操作点击图形界面的时间，提高了效率。

缆车架的下框需要承载乘客的重量， 上框需要承载空调等配套设备的重量， 顶梁需要承载冰雪载荷， 上边梁、下边梁和底梁需要承载挡风玻璃和门的重量，因此需要校核缆车架型材框架在承载极限载荷工况时的位移和应力是否满足要求。

有限元理论的核心思想是“离散化”与“数值近似”，其主要求解过程是将一个连续变化的求解区域离散成为若干个有限的单元，单元和单元之间通过节点相互连接，采用多项式的位移模式， 单元上任意点的解可以写成插值多项式形式， 单元特征即可使用节点的未知参数来表示，通过建立每个单元关系方程，联立方程组并求解，则可以得到每个单元内部节点处的未知参数， 通过插值函数可以得到单元上任意点的近似解。 通过进一步控制单元尺寸，满足收敛条件，可以得到更加精确的近似解。

本文缆车架空间上是由多个梁拼接而成， 在ANSYS有限元软件中可以使用梁单元进行求解， 相对于杆单元只能承受轴向力，梁单元还能够承受弯矩和剪力。梁单元可以用于三维模型结构中， 它能够将三维模型一维理想化，因此相对于壳单元与实体单元，梁单元的求解效率也更高。 ANSYS 软件中定义了两种类型的梁单元， 分别是beam188 梁单元和beam189 梁单元， 且这两种类型的梁单元均有较强的适应性和计算能力，能够自定义梁截面，能够解决复杂的异形截面结构的力学分析。 beam188 和beam189 单元一般情况下都可以选用， 其基本理论原理是相同的，两者的不同为beam189 单元是三节点单元，而beam188 单元是二节点单元。

beam188 单元是考虑分析对象的剪切变形， 基于铁摩辛柯梁理论的一种三维二节点梁单元， 能够用于分析从细长到中等粗/短的不同长度范围的梁结构。 beam188单元的每个节点处均有6 个或者7 个自由度，使用KEYOPT（1）命令赋值可以控制自由度的个数，该单元能够选择一次、二次或三次形函数进行插值。 beam188 单元包括的关键字选项如下：K1、K2、K3、K4、K6、K7、K9、K11、K12和K15， 关键字K1 可以用来设置是否考虑翘曲自由度，关键字K2 可以用来设置单元横截面缩放比例， 关键字K3 可以用来设置单元沿长度方向的形函数。

通过自下而上的建模方法建立缆车架的有限元模型，首先生成缆车架的关键点，然后通过关键点生成线，最后通过线以及自定义梁截面生成缆车架的网格模型。定义缆车架的参数值，便于对各参数进行修改。使用命令K 定义缆车架上的关键点，使用命令LSTR 定义缆车架上的直线，使用命令LARC 定义缆车架上的圆弧线，缆车架上需要定义的直线和圆弧线较多，通过使用*do 和*enddo 命令执行循环以减少输入的命令行数。 缆车架内各零部件均选用Beam188 单元， 该单元为二节点单元。 使用MP 命令定义线性材料属性，包括弹性模量、泊松比和密度，缆车架均为铝合金结构。

以上通过创建缆车架关键点生成直线和圆弧线的方式对梁长度方向进行了定义，下面需要创建梁横截面。缆车架内部一共包含六种梁横截面形式，均为不规则截面，因此无法直接使用ANSYS 软件中的11 种常用的横截面库， 需要对梁截面进行自定义。 通过自定义梁截面，在ANSYS 软件中创建截面的2D 模型并完成面网格划分，使用SECWRITE 命令保存到ANSYS 软件的工作目录下，即可使用SECREAD 命令加以调用。 使用SECOFFSET 命令可对截面位置进行横向偏移， 六种横截面生成的面网格模型见图3。

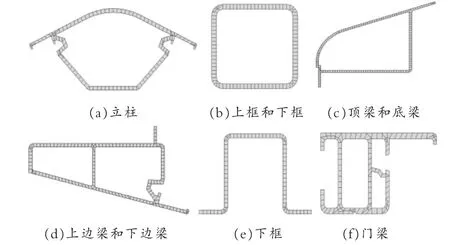
图3 横截面面网格模型

ANSYS 有限元软件中的网格划分策略包括自由网格划分和映射网格划分， 合理的网格划分直接决定了计算结果的准确性，因此网格划分是ANSYS 有限元数值仿真中非常重要的一环。自由网格划分应用范围更广，不仅可以用于规则的几何实体，也可以用于复杂的、不规则的几何模型，如空间曲面、异形结构等形状，单元形状可以选择三角形、四边形或四面体，网格的密度可以通过控制网格的数量、单元边长等实现。映射网格划分一般只能用于较为规则的模型，如规则的曲线、曲面、实体等形状，单元形状可以选择三角形、四边形、四面体、五面体或六面体，网格密度需要通过严格控制网格数量、单元边长来实现。

ANSYS 软件中优质的网格划分不仅可以缩短求解时间，而且能够得到精确的求解结果。 网格划分的步骤包括选择单元类型、单元形状、网格密度等，同时需要做到先粗后细、由简入深、二维单元和三维单元搭配使用的原则。

使用LATT 命令将单元属性、材料属性、横截面的网格模型与未划分网格的缆车架线实体相关联， 而后使用LESIZE 和LMESH 对缆车架各梁单元轴向的线实体进行网格划分， 从而生成缆车架的体网格模型， 即有限元模型，有限元模型建模过程见图4。

图4 有限元模型建模过程

2.2 有限元模型载荷施加与求解

ANSYS 软件中，载荷不仅可以是力，也可以是位移、速度等，因此载荷包括内外部作用力和边界约束条件。具体的，结构分析中的边界约束条件一般为位移约束条件，多表现为不同方向的自由度约束， 主要包括x、y、z 三个方向的平动位移约束和x、y、z 三个方向的转动位移约束。 缆车架顶部有四个吊点， 对其施加完全约束， 使用ESEL 命令选择需要施加约束的单元，使用D 命令约束单元的自由度。 四处约束点坐标分别为A1（a/2，b/2，h1）、A2（a/2，-b/2，h1）、A3（-a/2，b/2，h1）、A4（-a/2，-b/2，h1）。 其中a=1238mm，b=1080mm，h1=2700mm。 使用ESEL 命令选择需要施加载荷的单元， 使用SFBEAM 命令对缆车架上的梁单元施加载荷。

载荷施加完毕，使用EQSLV 命令选择求解器，然后使用SOLVE 命令进行求解，ANSYS 软件中可以选择5 种不同的求解器进行求解， 分别对应了5 种不同的求解代数方程组的方法，其中ANSYS 软件中的默认缺省解法为稀疏矩阵直接解法。

求解完成后，需要查看分析的结果，使用/POST1 命令进入通用后处理。 ANSYS 软件中带有两个后处理器：分别为通用后处理器 （POST1） 和时间-历程后处理器（POST26）。 其中POST1 可以查看模型在特定的时间点或载荷步的分析结果，POST26 可以查看模型在特定点的结果随时间的变化。 由于需要查看载荷施加完毕后缆车架的应力、位移等情况，因此选择POST1 后处理器。

使用NSEL 命令选择缆车架顶部的约束点， 然后使用PRRSOL 命令可以得到节点处的支反力， 即固定吊点所需要的力。 通过提取得到四个约束点的约束反力及合力分别如下： 约束点A1 约束反力为Fx=-1976.5N，Fy=575.15N，Fz=-271.02N，合力为2076.25N， 约束点A2 约束反力为Fx=-1750.9N，Fy=-564.33N，Fz=-450.84N，合力为1894.04N，约束点A3 约束反 力 为Fx=-1021.9N，Fy=-1913.1N，Fz=3286.6N， 合 力 为3937.76N， 约 束 点A4 约 束 反 力 为Fx=-1268.1N，Fy=1902.2N，Fz=3468.3N，合力为4153.98N。通过比较，可得吊点所需的最大约束力为4153.98N，如考虑最小1.25 的安全系数，建议吊点结构紧固件受力需大于5192.48N。缆车架的应力最大点在上边梁上，位移最大点在底梁上，缆车架的应力和位移云图见图5， 最大位移达到5.896mm，最大应力达到32.4MPa，因此缆车架能够满足承载要求。

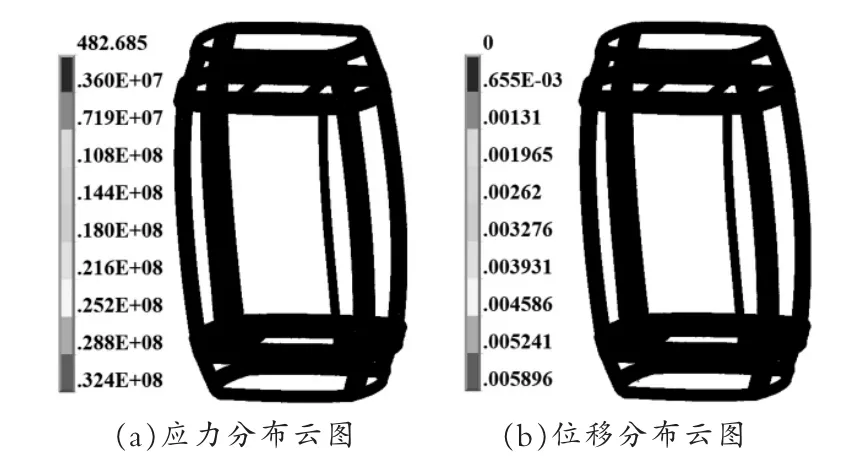
图5 仿真结果

3 结论

分析了缆车内部承载结构件缆车架的机械组成结构，得到缆车架所受的外部载荷，包括乘客的额定载荷，极限风载荷，冰雪载荷和门、挡风玻璃载荷。

建立了基于APDL 的缆车架参数化有限元模型，得到缆车架顶部吊点固定所需的约束力以及缆车架的最大位移和应力，为缆车架的进一步设计优化提供理论参考。