基于遗传算法优化PID的电磁制热系统温度控制方法＊

徐逸扬，潘兆一，李锦键

（1.兰州理工大学电气工程与信息工程学院，甘肃 兰州 730050；2.甘肃新农生态能源环保科技有限公司，甘肃 临洮 730500）

作为一项新型加热技术，电磁制热凭借着加热速度快、热量利用效率高、安全环保、使用寿命长等优点，现已在农业、工业以及日常生活等多个领域中得到广泛应用［1］。

常见的电能取暖方式主要有电阻式制热取暖和电磁制热取暖。其中，电阻式制热取暖是利用电流流过导体的焦耳效应产生热能实现取暖；电磁制热是利用交变磁场，在铁质金属内部形成涡流进而产生热能实现取暖。但电阻式制热取暖存在能量损耗大、速度慢、不安全等明显缺点［2］。相同条件下，电磁制热取暖的加热效率可达90%以上，预热时间相较于传统电加热可缩短60%以上［3］。并且电磁制热取暖具有寿命长、安全可靠等优点。故电磁制热取暖更优。

目前，许多领域对加热对象的温度控制精度要求较高，因此对提高电磁制热过程中温度控制的研究具有十分重要的意义。文献［4］将PID控制与模糊控制理论结合在一起，实现了参数的在线自整定。文献［5］比较了PID控制与fuzzy－PID控制在稳态误差、调节时间等方面的特点，通过仿真对比可知，fuzzy－PID控制能够加快升温速率，减小系统的超调量，且有更为优良的控制精度。以上文献均采用模糊控制优化PID参数，有效地控制电磁制热系统温度，但没有结合人工智能算法优化PID参数。

本文从温度控制策略入手，提出遗传算法优化增量式PID的电磁制热温度控制方法，使得电磁制热系统加热速度更快、加热效果更为均匀，为电磁制热系统温度控制技术能够应用在更广泛的行业提供实验分析和参考。

1 电磁制热温度控制系统建模

电磁制热控制系统是由控制器、电磁制热电源、感应加热线圈、被加热层合板及红外温度传感器组成，图1为电磁制热控制系统的各个环节的组成模式。

图1 电磁制热温度控制系统

1.1 电磁制热系统各环节传递函数

1.1.1 电磁制热电源环节传递函数

电磁制热电源的主电路由整流电路和逆变电路构成，如图2所示。

图2 电磁制热电源主电路

整流电路的作用是将单相工频电流整成脉动直流，为逆变电路提供稳定的输入；再通过逆变电路输出端为电磁制热控制系统提供稳定的电源。电磁制热电源主电路中的逆变环节可以等效成一个增益环节，输入为直流母线电压U，输出为逆变后输出的有功功率P，在忽略电源扰动的情况下，P的大小与U成正比，其传递函数可简化为：

式中，Km为增益。

1.1.2 感应加热线圈环节传递函数

1.1.3 层合板导热环节的传递函数

分析电磁制热在单位时间内所产生的热量、材料的密度以及比热容等物理特性之间的关系，并结合热力学可得到层合板导热环节的传递函数［7］：

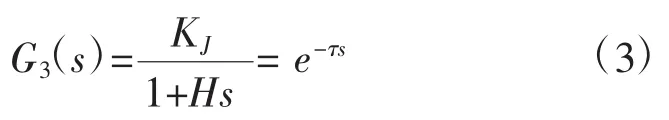
式中，KJ为层合板导热环节增益；H为电磁制热时间常数；层合板导热环节在电磁制热控制系统中存在滞后特性，所以在当前环节中加入延迟环节e－τs。

1.2 电磁制热系统温度控制的传递函数

综上分析电磁制热系统的电源环节、感应加热线圈环节及层合板导热环节，得到电磁制热系统温度控制框图如图3所示。

图3 电磁制热系统温度控制框图

其中：

（1）GC（s）为控制器环节的传递函数；

（2）G1（s）为电源环节的传递函数；

（3）G2（s）为感应加热线圈环节的比例系数；

（4）G3（s）为复合材料层合板导热环节的传递函数；

由以上分析可知，感应加热控制系统的开环传递函数为：

2 电磁制热温度控制算法实现

2.1 增量式PID算法简介

在电磁制热控制过程中采用增量式PID算法来实现温度控制，主要为三个参数：比例增益KP、积分时间Ti、微分时间Td。其计算过程如式（6）所示：

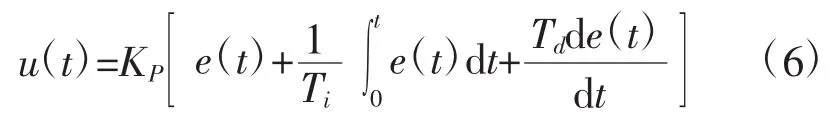
式中，u（t）为控制量；KP为比例控制环节系数；e（t）为系统偏差，e（t）＝yS（t）－yR（t），其中yS（t）为系统设定值，yR（t）为实际测量值；Ti为积分时间环节系数；Td为微分时间环节系数。

将式（6）中u（t）转化为离散形式u（k），经过整理后，可将第i次采样时刻控制量的增量Δu表示如下：

2.2 遗传算法优化增量式PID

遗传算法是一种基于生物界进化理论和生物遗传机制的随机搜索算法。本文采用遗传算法优化增量式PID算法中的参数，并应用于电磁制热系统，以实现对温度更为有效地控制。

遗传算法优化增量式PID算法是利用遗传算法对增量式PID的各个控制参数（Kp，Ti，Td）进行寻优，得到性能指标 J＝g（Kp，Ti，Td）的最优结果。实现遗传算法优化PID参数需要完成以下四个方面的工作：

（1）参数确定

根据温度控制的特性，确定参数 Kp，Ti，Td的大概范围，然后根据参数的精度以及实际情况的要求，对参数进行编码，并设定遗传算法的各种初始参数。

（2）选取初始种群

随机生成初始种群，并产生一定数量的随机数，设定种群规模。

（3）选取适应度函数

以温度超调量、温度调节时间和动态温度偏差等指标来判断PID参数是否为最佳。选用式（8）作为优化目标函数［8］：

式中，w1，w2，w3为加权系数，且有w3≫w1；ts为系统调节时间。

遗传算法的适应度函数由目标优化函数转换得到，目标优化函数J值越小，控制系统的质量就越好。故适应度函数为：

（4）种群的复制、交叉与变异

在一个旧种群中选择生命力强的个体产生新种群的过程称为复制。本文使用适应度比例选择法进行复制运算，若某个体的适应度为Fi，则其被选中的概率 Pi为［9］：

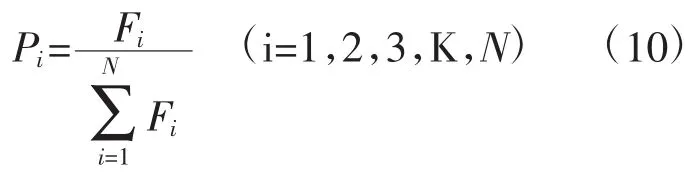
复制运算结束后，由交叉运算和变异运算得到下一代种群，其中，交叉算子概率为Pc，变异算子概率为Pm。在进化后期，为保护已有的优良个体，采取Pc、Pm自适应调整方法［10］，在一定程度上保护了进化后期的最优个体，又降低了局部收敛的可能性。Pc和Pm的动态调整公式为［11］：

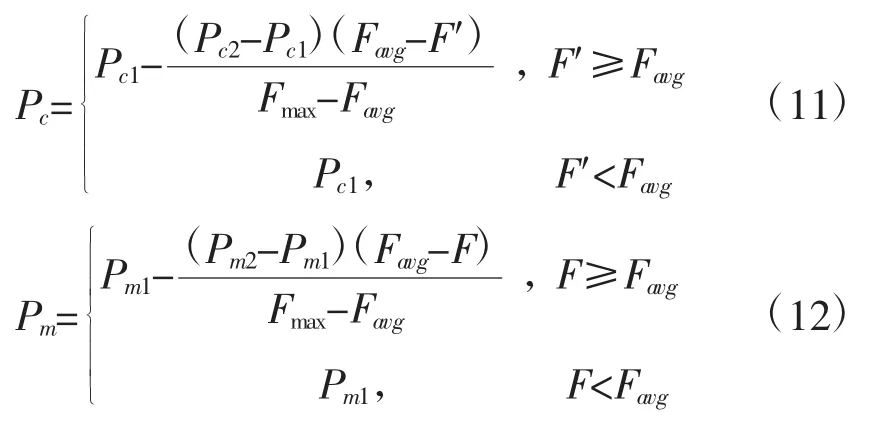
式中，算子概率 Pc1，Pc2，Pm2∈（0，1）；Favg为个体适应度平均值；Fmax为个体适应度最大值；F′为进行交叉的个体中适应度函数值的较大值；F为待变异的个体适应度函数值。

2.3 算法实施的具体流程

遗传算法优化增量式PID的具体流程如下所示。

（1）设置种群规模M，总进化代数G；设置参数Pc1，Pc2，Pm2，Pm2，w1，w2，w3；初始化进化代数D＝0；

（2）定义参数KP、Ti、Td的范围，并对KP、Ti、Td进行编码；

（3）随机生成规模为M的初始种群；

（4）计算其目标函数优化值以及各个体的适应度；

（5）进行选择与复制；计算交叉概率，进行交叉运算；计算变异概率，进行变异运算；

（6）进化代数D＝D＋1，得到新种群P（T）；

（7）判断D是否小于G，若为是，则重复（4）到（6）；若为否，则解码并输出最优解。

3 仿真分析

在温度控制中，输入变量为温度偏差，通过对控制器参数进行调整，达到调节电源占空比的目标，进而改变电源输出功率，最终完成对电磁制热系统的温度控制。在控制系统稳定时，功率调节变化较小，且温度变化较快，一般情况下系统的延时时间为0.5秒。设置加热最高温度为45℃，且未加入PID环节，仅在系统中形成闭环控制时，电磁制热系统升温曲线仿真结果如图4所示。

图4 无PID控制器的电磁制热系统升温曲线图

当电磁制热系统中采用增量式PID控制时，根据增量式PID控制算法，选取参数为KP＝12.5，Ti＝0.5，Td＝0.1，其升温曲线仿真结果如图5所示。

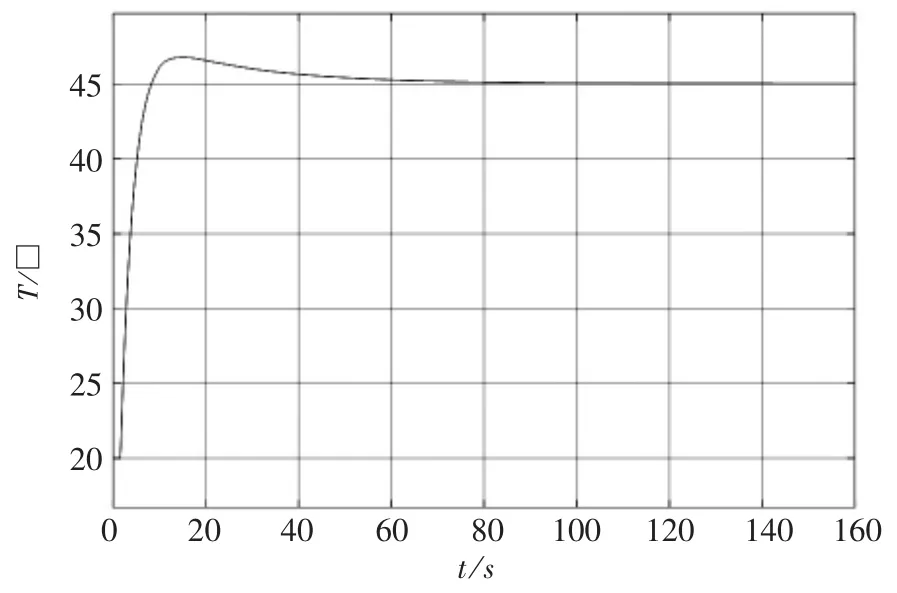
图5 加入PID后的电磁制热系统升温曲线图

对比图4和图5可知：未加入PID环节时，电磁制热系统温度虽然在逐步上升，但温度上升速率较小，进入稳态所需的调节时间较长；加入PID环节后，电磁制热系统的温度上升速率显著提升，且达到稳态温度所需的调节时间大幅度缩短。

为验证改进遗传算法优化PID参数控制策略的优越性，设定总进化代数G＝500，定义参数范围：KP∈［0，50］；Ti，Td∈［0，3］；经过复制、交叉与变异，在输出最优结果后进行温度响应速度模拟测试。

采用遗传算法优化后，将PID控制器的参数调整为 KP＝40，Ti＝2.5，Td＝0.1，对电磁制热系统进行仿真，得到升温曲线，并与图5的升温曲线进行对比，得到如图6所示的升温曲线对比图。其中，曲线①为采用遗传算法优化PID参数前的升温曲线，曲线②为采用遗传算法优化PID参数后的升温曲线。

由图6可知，采用遗传算法优化PID参数之后，温度上升速率得到进一步提升，在达到设定温度后，会产生一个小范围的超调量，超调量为4.4%，调节时间为40s。进入稳态后，稳态误差很小，且稳态温度基本趋于设定值，上升时间为tr＝4s。由以上仿真结果可知：采用遗传算法优化增量式PID的温度控制方法既降低了升温过程中的超调量，同时又保证了温度的控制精度。

图6 优化PID参数前后电磁制热系统升温曲线

4 结论

本文通过对电磁制热系统的数学模型进行分析，建立了温度控制传递函数，使用增量式PID算法来实现控制系统的温度闭环控制，并采用遗传算法实现对PID参数优化。通过仿真验证表明：相较于传统PID算法，采用遗传算法改进增量式PID后，电磁制热系统的升温速率明显加快、超调量明显减小、制热温度很快进入稳态且稳态误差很小，稳态温度基本趋于设定值；采用遗传算法改进增量式PID实现了对电磁制热系统的温度有效控制，在保证电磁制热系统稳定工作的情况下，能够准确控制加热温度。