非线性Volterra模型预测最小方差法控制钻压系统

石俊龙，刘志臻

（1.中石化海洋石油工程有限公司上海钻井分公司，上海 201208；2.天水天传电气工程有限责任公司，甘肃 天水 741020）

在油气生产的钻井作业中，一项关键任务是井压控制，尤其在海上钻井平台。钻井过程是一项具有挑战性、高成本的作业，许多先进的技术和自动控制技术已被采用，以提高效率和成本效益［1］。压力控制钻井（MPD）作为一项突出的技术被引入，可在井筒压力控制中提供更高的精度、安全性和更快的响应。MPD控制系统将井底压力保持在井缘内，即高于储层压力（超平衡钻井作业）。与传统钻井中的手动交互不同，上部节流阀由自动控制系统操纵以实现控制目标，并能够在非常窄的压力窗口内进行钻井作业［2］。自动MPD控制系统在紧急情况下提供更大的灵活性（例如从储层涌入的流体，通常称为可能导致井喷的井喷），并有效地恢复系统性能。

MPD控制系统设计的一个重要步骤是推导水力模型。开发了先进的液压模型来捕捉钻井液压的不同方面［3－6］，需要注意的是控制目的和实际应用，因此，MPD的自动控制系统通常采用简化的水力模型。有学者［7］提出了一种层次方法，其中PID控制器和模型预测控制（MPC）在具有三个不同级别的多级控制结构中结合，但这项研究没有考虑控制过程中的反冲缓解。为了调节环空压力并减弱油藏反冲，设计了一种自动MPD系统的切换控制方案［8］。反冲检测和通过钻头的流速估计是由自适应观测器实现的。预测控制是一种先进的控制策略，已用于MPD系统。还有人中提出了一种线性MPC［9］，其中井下压力控制是通过操纵节流开口和泥浆流速来获得的，尽管没有考虑反冲处理。

在实际应用中，MPD系统会受到不可避免的干扰，例如测量噪声和具有随机性的起伏运动，这对可实现的控制性能造成了限制［10］。此外，特别是在海上应用中，钻井经常经历压力和流速的振荡状态，这就需要对MPD过程进行随机处理。方差是过程控制中广泛使用的随机性能标准，关键井变量方差的减少使系统能够在减少能源消耗和维护成本、提高产量以及节省原材料的约束条件下工作。最小方差（MV）控制器已在工业中广泛应用［11－13］。由于在瞬态水力模型的某些组件中观察到相当大的不确定性，包括钻井液的粘度、流变、摩擦压力损失和有效体积模量，因此必须研究设计控制方案的稳健性能。同样，在海上钻井中，升沉扰动会明显影响MPD的运行，并且现有的NMPC研究没有考虑控制器在处理升沉扰动时的鲁棒性。

本研究通过提出约束非线性预测广义最小方差（NPGMV）控制来解决MPD系统的控制问题，其中水力模型以自回归非线性Volterra模型的形式识别。Volterra级数模型广泛用于非线性系统的研究，不需要关于系统动力学的经验知识。所提出的控制方案使用输入输出操作数据，不需要详细的数学水力模型。切换结构用于在发生蓄水池反冲时提供反冲处理。此外，还考虑了一些情况，例如具有挑战性的管道连接程序，以评估所提出的控制方案的有效性。

1 数学模型

在自动MPD系统中，主要控制目标是保持井底压力满足钻井作业期间地层的工作压力范围。图1为自动MPD系统的典型配置示意图。MPD系统的简化模型由两个主要控制体描述，即环空侧和钻柱。在钻井过程中，钻井液（泥浆）在钻柱、环空控制容积和钻头中循环，泵送的泥浆通过钻头从井底出来，并将岩屑输送到钻机上。在返回路径上，泥浆流通过顶部的节流阀，该节流阀的安装是为了提供所需的压力。

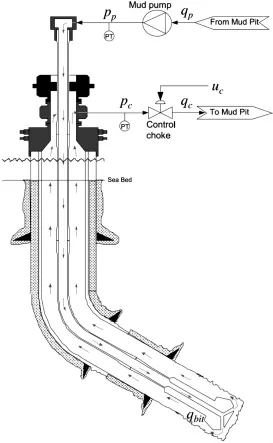
图1 自动MPD系统

环空节流压力和泥浆泵压力的动态模型是由质量和动量守恒原理得出的：

其中，qc、qp和qbit分别是通过扼流圈、泥浆泵和钻头的流量。另外，Vd和βd是钻柱体积和有效体积模量，Va和βa是环空体积和有效体积模量，qkick是反冲流量。穿过钻头的流动可以描述为非线性常微分方程（ODE）。

其中，M是恒定质量密度，ρa和ρd是泥浆密度，fa和fd分别是环空和钻柱中的摩擦系数。hTVD是井的实际垂直深度，重力常数用g表示。主要变量井底压力Pbh，定义为：

此外，非线性孔口方程为：

其中，uc表示实际节流开度，取值范围为［0，1］。Cd称为流量系数，节流下游压力用P0表示，Ao表示孔口面积。反冲流速由方程式为：

其中，Prse是储层压力，Kpi与储层特征有关。

2 方案设计

通过操纵节流阀uc调节井底压力Pbh的控制策略设计。尽管钻井窗口窄、气涌、外部干扰和系统物理限制等，但所提出的控制器必须将井底压力保持在所需设定值。Volterra级数模型已被证明可以有效地模拟非线性系统，也可以用作预测模型。具有输入uc、输出Pbh和扰动x的MPD系统可以建模为一般自回归二阶Volterra系列单输入单输出（SISO）模型：

其中，ε（k）是方差为零均值白噪声输入。模型偏移由h0考虑，A、B1、B2和C是后向移位算子中q－1的多项式，具有以下结构：

要在NPGMV控制设计中使用预测模型，应确定指定的Volterra模型参数。开环识别是通过将具有五个不同级别和八个步骤的多级序列应用于MPD系统的节流阀来执行的，见图2。

二阶沃尔泰拉级数模型通过最小二乘法识别，因为模型在参数上是线性的。采样时间为Ts＝2s，延迟选为1次采样。最后，识别模型中多项式的阶数选择为 nA＝2、nB1＝1和nB2＝1。识别的Volterra模型与应用于非线性的识别数据集通过比较如图2所示。验证结果表明，该模型可以成功地描述非线性系统的动态行为。计算归一化均方根误差（NRMSE）标准以检查识别性能，并具有91.2213%的可接受拟合度，图3为闭环控制系统图。

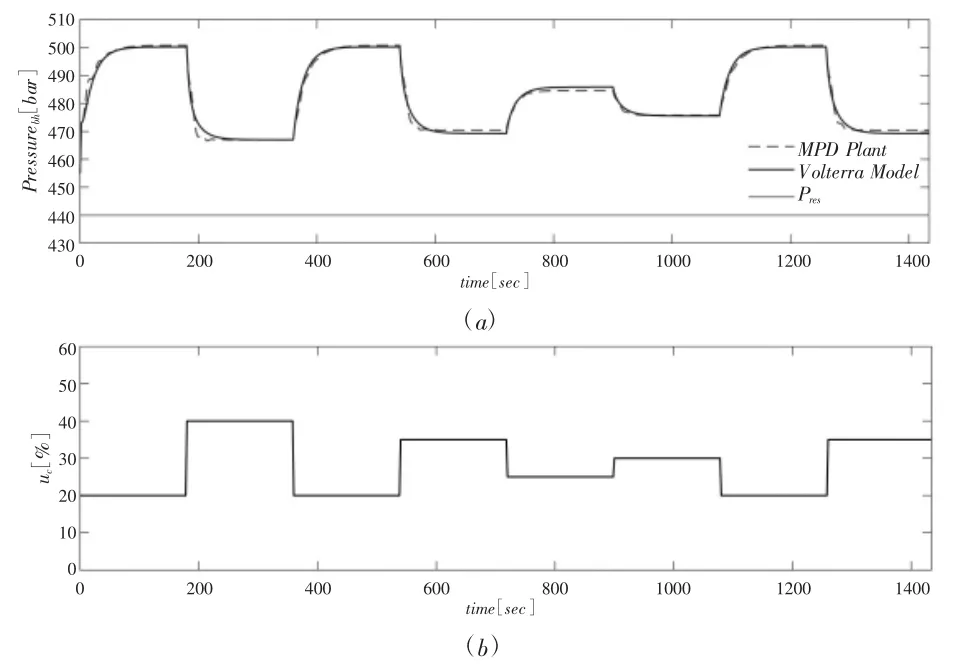
图2 非线性输出与Volterra模型比较

图3 闭环控制系统图

3 仿真结果

NPGMV控制策略在描述的MPD系统上实施。提供了各种场景来说明控制器在噪声、物理约束和系统不确定性下的性能和鲁棒性。此外，仿真采样时间设置为Ts＝2s。为了进行比较研究，设计了一种开关PI结构并将其应用于系统。

在模拟过程中，泵送的泥浆流速保持恒定在1200lpm，这在正常钻井作业中很常见。初始储层压力假定为pres＝465bar，但为了评估控制器的反冲处理性能，我们将储层压力逐渐增加到480bar，并在t＝400秒时发生反冲。在NPGMV控制器中，考虑δ＝2bar。图4、图5显示了使用切换PI控制和NPGMV控制的闭环结果。从图5可以看出，尽管两个控制器在设定点跟踪方面都表现良好，但与切换PI相比，NPGMV控制器响应更平滑并提供更好的性能控制器。结果表明，在切换PI控制器下系统的输出存在超调。在稳态方差方面，NPGMV控制器性能的优越性得到了明显体现。ISE和IAE指数证实了所提出的控制方案的有效性能。从井喷处理的角度来看，一旦井喷事件发生在t＝400秒左右，NPGMV控制器通过从压力调节模式切换到流量控制模式来处理油藏流体流入问题。关闭压力调节会导致井底压力增加。根据图4，NPGMV控制器代表了良好的冲击衰减，并将井底压力保持在储层压力之上。然后，开启NPGMV控制器压力调节以继续设定点跟踪。图4中的切换PI控制器响应显示控制器试图处理储层井涌，但不如NPGMV控制成功，因为它会导致井中的井涌流。

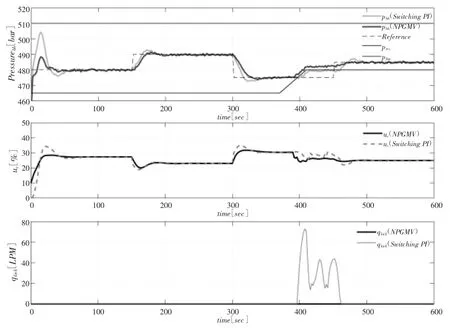
图4 正常钻井条件下的设定点跟踪和反冲处理

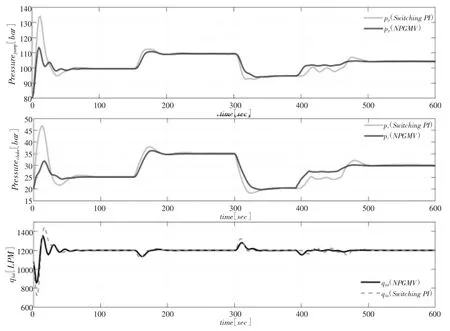
图5 正常钻井条件下的闭环响应

4 结论

本文将最小方差控制概念应用于钻井作业自动控制系统。针对需要井底压力控制和反冲处理的MPD系统，提出了NPGMV控制方案。MPD系统的水力流动模型由输入－输出数据获取的自回归二阶Volterra模型识别。所提出的控制方案可以处理具有挑战性的约束问题，在钻井作业中要求很高。在此设计中，来自已知和未知源（例如测量噪声）不可避免的干扰影响被视为包含在预测模型中的加性输出干扰。上部节流器用于控制井底压力。所提出的控制方案可以有效地管理紧压窗口内的钻井作业。此外，当观察到油藏流入时，控制器激活流量控制模式以抑制油藏反冲。所提出的控制器能够在泥浆泵流量急剧下降的情况下保持井底压力高于油藏压力，这通常发生在管道连接过程中。仿真结果表明所提出的方法与切换PI控制相比具有优越性，表明NPGMV控制显着降低（63%）海上钻井中升沉扰动的影响。鲁棒性分析结果证实了该控制方案在模型存在不确定性的情况下具有令人满意的性能。