基于锚节点的无线传感网离群值检测算法
衷卫声,罗力维,张强
(南昌大学a.信息工程学院,江西 南昌 330031;b.先进制造学院,江西 南昌 330031)
随着电子技术和无线通信的不断发展,无线传感器网络(wireless sensor network,WSN)应运而生,它广泛应用于定位、导航、工业和军事等领域。由于WSN在系统稳定性、可靠性、感知信息的准确性等方面存在不少问题需要解决,这可能会导致传感器数据不可靠、产生噪声、数据丢失与冗余,从而影响到原始数据的质量和汇总结果,所以需要离群值检测算法[1-3]。
目前,WSN中离群值检测方法大致分为基于统计的方法[4]、基于最近邻的方法[5]、基于聚类的方法[6]以及基于分类的方法[7-9]等。其中,基于分类的方法是机器学习的重要领域,而一分类支持向量机(OCSVM)是其中最流行的方法之一。它不断地将低维数据投影到高维空间中并且形成边界,将边界外部的数据判断为离群值,通过最大化决策边界的余量为分类提供最佳解决方案。此外它还能通过核函数简化投影计算从而避免维数诅咒的问题。为了更好地将OCSVM用于WSN中,Rajasegarar等[10]将OCSVM的边界拓展为球和椭球,并以此为基础形成了四分之一球支持向量机(QSSVM),以及中心椭球支持向量机(CESVM)。这两种算法在运行过程中将球心移到坐标原点以计算支持向量,因此也增加了计算量,不适用于大规模的WSN。Miao等[11]将OCSVM应用于大规模的WSN并且摒弃了融合中心(FC),从而形成分布式网络。此外,Miao等[11]还在应用过程中使用随机近似函数代替核函数,从而节省了计算资源。但随着分布式网络规模增大,每个节点的实际情况都各不相同,因此每个节点的OCSVM参数设置都应该不同。在机器学习中,OCSVM的错误容忍度参数υ和边界调整参数γ是对其检测效果影响最大的两个参数。Wang等[12]通过找到最大和最小的γ参数,并且将其平均值作为最佳的参数。但是以这种方式选择γ参数可能会有很大的波动。为了解决这个问题,Xiao等[13]提出计算从数据集到OCSVM封闭表面的距离,然后在此基础上,提出了参数选择的优化目标函数。Anaissi等[14]则对算法做了进一步扩展,使其更适合于高维数据集。
然而,上述参数设置方法可能不适用于WSN。因为在WSN中要考虑各种因数的影响,如节点之间的相关性、时空性等,所以每个节点的参数应该自适应地调整。本文提出一种基于锚节点的无线传感网离群值检测算法,将定位算法中的锚节点引入检测算法中,以锚节点与节点属性之间相关性为基础,利用大小根堆与标准差来动态地调整普通节点的参数,并将其转换为锚节点,循环往复地拓展到整个无线传感网,最终每个节点的参数都自适应地调整为最佳。
1 OCSVM算法
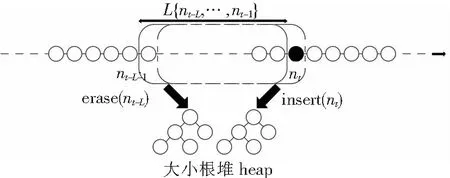
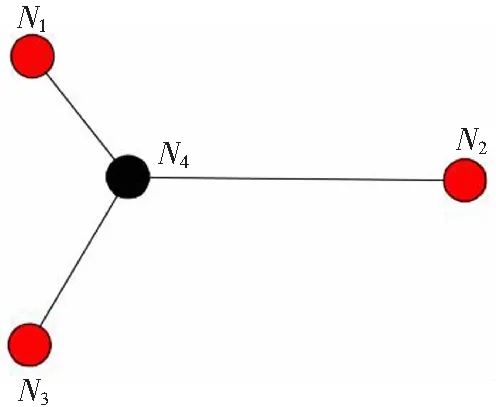
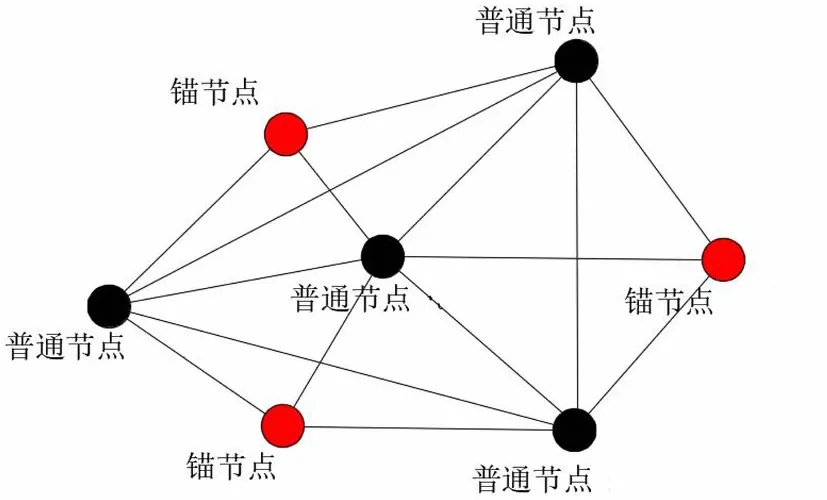
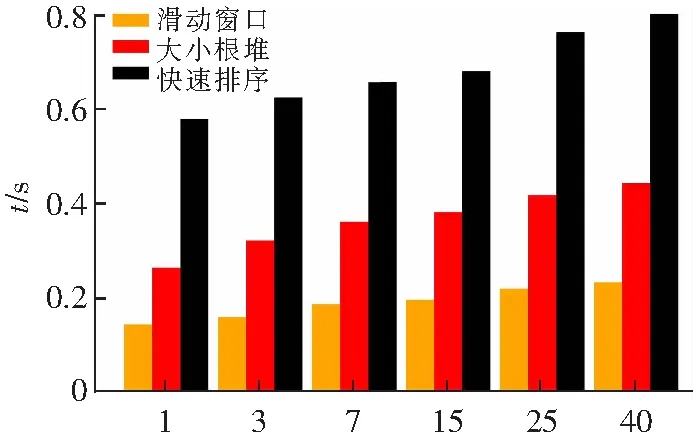
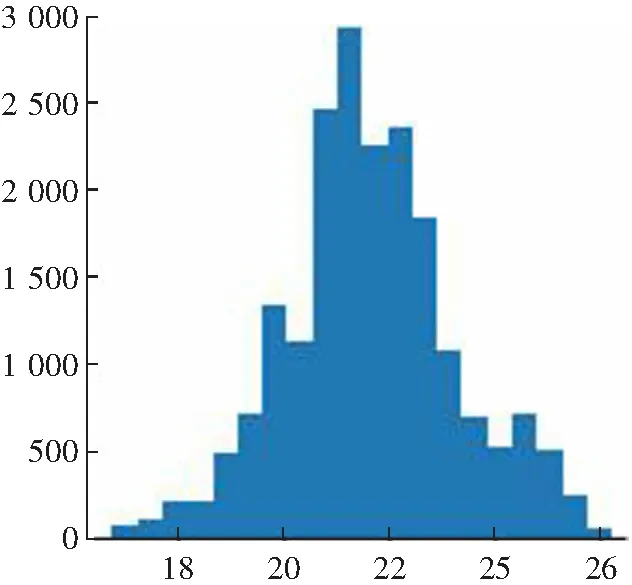
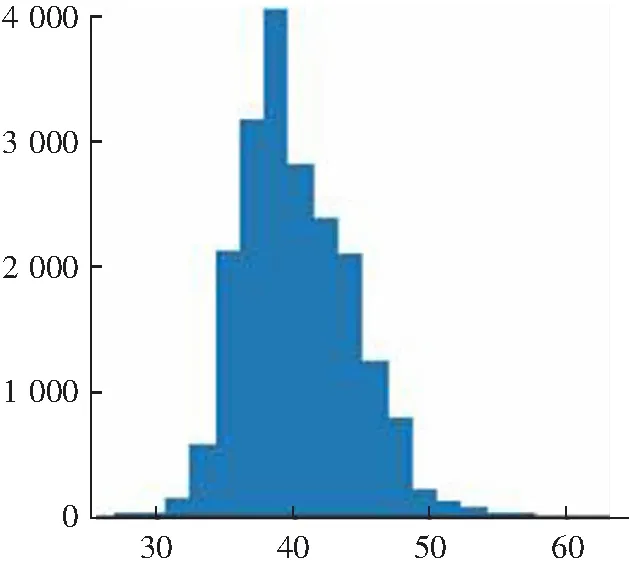
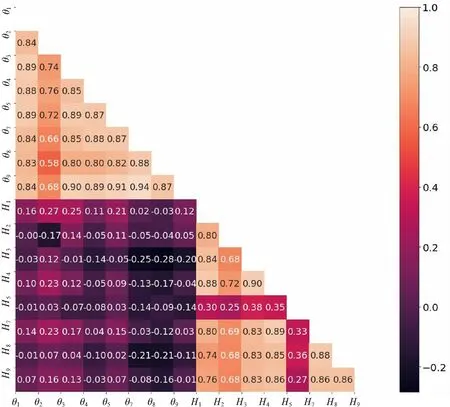
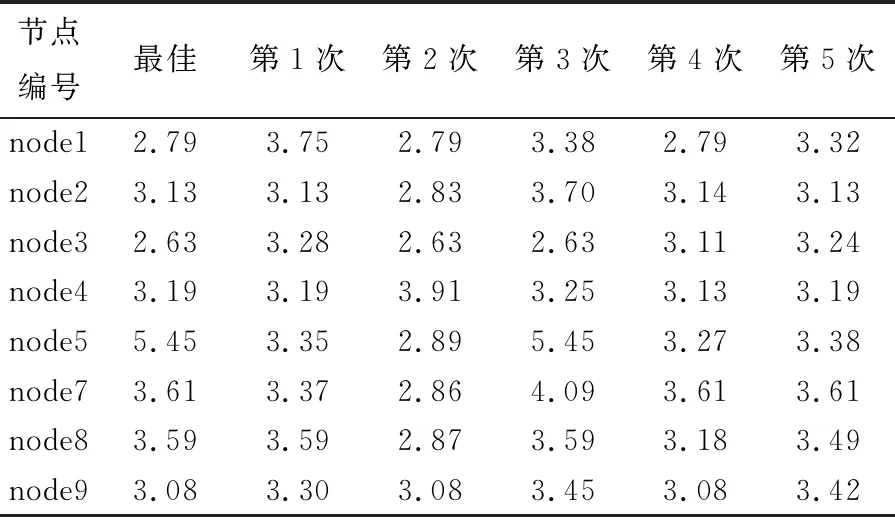
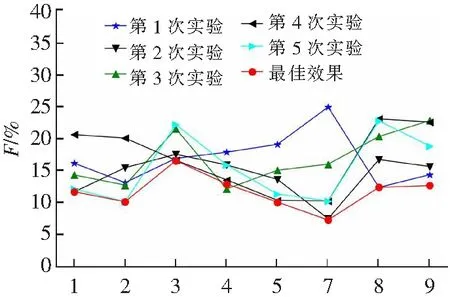
Schölkopf等[15]提出了一种称为OCSVM的分类方法,用于在高维现实世界数据集中进行离群值检测。对于给定的数据集,OCSVM算法将在正常数据的密集区域周围找到边界。位于边界上或内部的数据被称为普通数据,否则为离群数据。但是,在实际情况下,数据并不总是线性可分离的。此时,我们可以选择将低维数据集Rd投影到高维特征空间Rd'上,其中d< OCSVM分类器的原始二次问题[16]为: (1) 式中:ω∈Rd,ξ=[ξ1,…,ξn]是松弛变量,ρ是偏差项,且0<υ≤1。 为了更好地进行计算,使用拉格朗日乘数法将式(1)转换为以下二次对偶问题: (2) 然而,持续的投影可能会导致大量的计算(甚至是不可能的)。此时,可以使用核函数代替投影计算。在本文中,通过使用高斯径向基函数(RBF)k(x,y)=e-γ||x-y||2来代替投影,从而减少计算量。 在OCSVM算法中,参数设置直接关系到整个模型的好坏,特别是容忍度参数υ跟决策参数γ。容忍度参数υ参数决定了OCSVM能识别的离群值比例,过大或者过小都会影响最终识别离群值的比例。而决策参数γ决定了整个OCSVM算法投影边界的复杂度,γ值过大则会让边界过于复杂,使运算复杂度增加,反之则会让边界变得简单,最后导致无法正确分离离群值。因此在导入OCSVM算法之前需要将υ与γ设置为合适的值。本文算法引入了定位算法中的锚节点,并且充分考虑各个节点之间的相关性,利用大小根堆存储周围锚节点的υ值,并取这些数据中的中位数作为自身的υ值。最后利用数据本身的标准差与相关性调整参数γ。 在数理统计中,平均数是总体均值很好的估计,中位数是对总体中心很好的估计,如果数据是来自某对称未知分布时,估计均值和估计中心是等价的。但就稳健性而言,中位数是较优于平均数。因为对于均值,只要有一个点无穷大,均值则会无穷大,但改变中位数至无穷大,则需要移动一半的数据,因此中位数要比均值稳健。 堆是一颗完全二叉树,在数据结构中常常用数组模拟二叉树,具体公式如式(3)所示。并且在堆中的某个结点的值总是大于等于(大根堆)或小于等于(小根堆)其子结点的值,并且堆中每个结点的子树都是堆树。 (3) 在建立堆的过程中,每来一个数据对应地插入时间复杂度为O(log2N)。并且在建堆的过程中,设总共N个元素,可以在大根堆存放m个较小的数,小根堆存放n个较大的数,当N为奇数时,应该满足式(4) m=n+1=(N+1)/2 (4) 当N为偶数时,应该满足式(5) m=n=N/2 (5) 此时,取中位数的公式如式(6)所示 (6) 各种常用取中位数数据结构的复杂度如表1所示。 表1 时间复杂度 可知,无序数组插入时间复杂度最小,适合频繁插入,但取中位数的时间复杂度较高。有序线性表查找快,但是数据结构的维护困难。平衡二叉树查找和维护相对均衡,但是存储的额外信息多(指针,子节点数),查找其他元素也很快。因此大小根堆是非常适用于查找中位数的算法,但是查找其他元素效率低。 因此可以维护两个堆,里面用来存放周围节点的υ,从而能随时随地地取出中位数的υ用来改变自己算法模型的参数。 但这也随之带来一个问题,在无线传感网中不一定需要周围所有节点的数据,可能需要不断地更新迭代。为此,本文引入了滑动窗口的概念,在无线传感网中维护一个固定大小的窗口用来存放周围节点的数据。当有新的数据来时,更新窗口,并且取出窗口中的中位数,具体滑动窗口的示意图如图1所示。 图1 滑动窗口示意图 在大小根堆算法中,只能增加元素,而不删除元素,因此需要增加删除元素的操作和对添加元素的操作进行修改。并且堆不支持随意删除除堆顶外的任何元素,所以本算法使用延迟删除,即,若该元素不在堆顶,则记录下该元素,等到该元素达到堆顶的时候再进行删除。延迟删除可以保证在任意操作之后保证大小根堆的堆顶元素是不需要删除的,因此能保证随时能取得中位数。改进后的算法示意图如图2所示。 图2 滑动窗口算法流程图 实现删除与插入所需实现设计的函数: (1)设计哈希表为hash=(n,num),用来表示元素n还需要删除num次。 (2)设计modify(heap)函数,不断弹出需要删除的堆顶元素,并减少对应的num值。 (3)设计balance()函数来封装modify(heap)函数,用来调整大小根堆的元素个数。 在balance()函数中,假设小根堆为A,堆顶为a1元素,大根堆为B,堆顶为b1元素。当需要调整大小时: (1)如果A=B,不调整; (2)如果A-B>1,将a1放入B中,通过调用modify(A)判断A的堆顶元素是否需要删除; (3)如果A>B,将b1放入A中,调用modify(B)判断B的堆顶元素是否需要删除。 综上,可以得到本算法所需erase(n)的步骤: 步骤1 如果n与大小根堆的堆顶不相同,将其在hash中的值加一,待其达到堆顶后便可将其删除,实现了延迟删除。 步骤2 若相同,可以通过延迟删除模拟立即删除,只需要将n在hash中对应的值加一,并且调用modify(heap)函数,就相当于实现了立即删除的功能 步骤3 在删除元素后,要调用balance()函数用来调整堆的大小 因此最终可以得到大小根堆跟滑动窗口的时间与空间复杂度如表2。 表2 复杂度 在OCSVM算法中,另一个重要的参数是γ,作为边界决策参数,它与数据的标准差存在一定关系。相关系数rXY的计算公式为: (7) 式中:Cov(X,Y)为X与Y的协方差;D(X)为X的方差;D(Y)为Y的方差,相关系数rXY越接近1则表示相关性越高,标准差S的公式为: (8) 定义3个锚节点,每个锚节点的υ,γ都是最佳,其与待定节点的关系图如图3所示。 图3 节点关系示意图 在图3中,N1,N2和N3为锚节点,N4为普通节点。根据标准差公式计算出锚节点中每一类数据特征的标准差。由于生活中绝大多数受随机因素影响的事物,基本上都符合正态分布,因此标准差越大,表示数据越离散。因为参数γ是边界条件,所以γ越大,边界会分得越细,但γ值过大会造成过拟合。所以可以假设锚节点γ的取值公式为: (9) 式中:F为所收集数据特征数。 假设每个WSN节点只收集温湿度两种特征,使用θ代表摄氏温度,H代表湿度,αi为i节点的平均相关系数。可得节点1和节点4之间的计算公式: (10) 式中:r为相关系数,则可以通过下式计算出普通节点的γ值与周围锚节点γ值: (11) 式中:m为锚节点数。 综上,检测算法的流程如下:锚节点预先设置υ值为最佳,并使用公式计算出γ值。普通节点通过寻找周围节点υ的中位数设置υ值和利用节点之间的相关性设置γ值,并且参数设置完之后,自身也转换成锚节点。节点通信示意图如图4所示。 图4 节点通信示意图 本文探讨的数据来源于文献[17],文章作者将其放入kaggle网站开源。整个数据集由9个ZigBee无线传感器网络收集温湿度而成。整个收集时间从一月到五月,共137 d,温湿度每10 min内取一次平均值,每个节点各收集了19 735组温湿度数据。从整个数据集来看,其涵盖了4.5个月的范围,使数据集有很好的完整性。并且其节点所处的环境具有差异性,有室内室外,室内还有不同的环境,如:浴室、卧室以及大厅等,这样保障了数据的多元性,从而保证仿真实验的真实性与有效性。 整个仿真实验设备使用第5代Intel Core i5CPU,12 GB RAW,开发平台使用JupyterLab,scikit-learn,语言使用Python。 在无线传感网中,单个节点的内存、运算能力以及电池能量都是极为珍贵的,所以整个算法的运算时间不宜太久,不然资源一直被占用会影响正常工作。 由于无线传感网的节点数可以非常大,因此用模拟数据检验查询中位数的性能。本文选择3种算法进行比较,滑动窗口、只寻求中位数的快速排序,以及大根堆与小根堆。随机产生1 000,3 000,7 000,15 000,25 000,40 000个不同的数,通过这3个算法寻找到中位数。而在滑动窗口中,每次只保存一半的数据和更新10个数据。通过比较插入时间(滑动窗口的时间取插入一半数据的时间加上更新的平均时间)与寻找中位数的时间,来综合比较各个算法的性能,不同数据量N所需的时间t如图5所示。 N/103 可以看出,随着数据量N的增大,通过大小根堆取中位数所花费的时间约为快速排序方法的一半。并且,引入了滑动窗口机制后,整个算法的运行时间进一步减少。此外,从额外空间复杂度来看,大小根堆都没有使用额外空间,都只是利用本来就存在的数据进行取中位数的过程。而快速排序有O(log2N)的额外空间复杂度。滑动窗口则是在利用哈希表的时候会产生O(N)的额外空间复杂度,其与需要延迟删除的元素有关。所以综合比对下来,通过大小根堆和滑动窗口取中位数的算法合适。 在数据集中,一共有9个节点,称节点1到节点9。其中,节点6处于户外,其湿度昼夜温差大与其余节点差异过大,为了避免出现较大偏差,所以将节点6去除,只分析余下8个节点。利用θ代表摄氏温度,H代表湿度,建立数据分布图,观察是否为正态分布,结果如图6、图7所示。 θ/℃ H 从图6与图7可以得出大部分的数据都接近于正态分布,因此节点数据的相关性可以通过式(7)计算,并且整个相关性如图8所示。 在图8中,颜色越深代表越不相关,越浅则代表越相关,可以观察出不同节点不同数据特征之间存在一定的相关性,只是这种相关性有强有弱。 图8 相关性 在OCSVM中,容忍度参数υ跟决策参数γ决定了整个算法的好坏。因此,在容忍度参数υ中,预先设置锚节点的参数υ与参数γ为最佳,周围的普通节点通过大小根堆与滑动窗口来获取自身的υ值。而参数γ,则是在验证相关性后之后,通过公式11自适应进行计算得出。独立重复做仿真实验5次,每次选取3个不同的锚节点,第1次锚节点为2,4,8,第2次锚节点为1,3,4,第3次锚节点为3,5,8,第4次锚节点为1,7,9,第5次锚节点为2,4,7,通过式(11)计算出的参数γ值如表3所示。 表3 γ参数 可以看出,在大部分的情况下,自适应获得的参数与最佳参数相比,只有20%~30%的误差,其中有部分参数与最佳参数接近一致。其误差大小与锚节点的选择有关,即事先要选取好锚节点,且锚节点之间不能相距过近,以免出现参数设置过于相近的情况。 在获取最佳参数设置后,还需要验证在所得参数设置下的算法是否将大部分正确的数据分离出来。混淆矩阵的定义如表4所示。 表4 混淆矩阵 为了检验上述参数设计对数据分离的效果,使用真阳性率T与假阳性F来进行比对,其T定义是算法正确分类且本身为正例的比例,F定义是将负例预测为正例的比例,公式定义如下: (12) (13) 将参数导入OCSVM算法中,其中圆形的折线为最佳参数,其余折线分别为1~5次独立重复实验的结果,所得结果如图9与图10所示。 节点编号 从图9中可以发现,整个算法的真阳性率T基本上保持在84.3%以上,这意味着绝大部分正常数据都被正确分离出来,而假阳性率F则大部分都在20%以下,这表明可以将大部分的异常数据分离出来。最后可以得出,参数γ与数据的相关性有关,并且可以良好通过滑动窗口、大小根堆所选择的参数υ将数据集的正常与异常的数据分离出来。 节点编号 本文以自适应调整无线传感网中离群值检测算法的参数为目标,结合锚节点与相关性提出了基于锚节点的无线传感网离群值检测算法。该算法以锚节点与节点属性之间相关性为基础,利用大小根堆、滑动窗口和标准差来动态地调整待定节点的参数,并将其转换为锚节点,循环往复地拓展到整个无线传感网,最终每个节点都能自适应地将参数调整为最佳。实验结果表明,在不使用额外的空间的情况下,利用大小根堆寻求中位数能够保持较低的运行时间。若可以使用一定的额外空间,利用滑动窗口机制则能够更进一步降低运行时间。并且也证实了标准差与参数γ存在一定的关系,可以通过相关性与标准差来设置参数γ,结果表示本文提出的算法能较好地辨识出正常数据。在自适应调整方式下,检测算法的真阳性率在84.3%以上,假阳性率在20%以下,并且能够将数据正确的分离出来。并且该算法适用于许多小型室内的无线传感网,这些网络必须事先将算法模型导入进去用来实时监控,并且传感器的CPU与内存资源有限。因此可以通过本文所提出的算法来进行设置参数,以达到比较良好的数据监测与分离的作用。2 无线传感网离群值检测算法
2.1 大小根堆算法设计
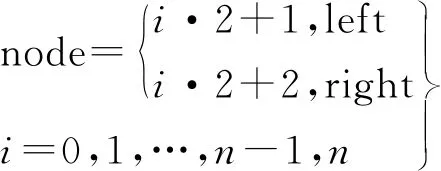

2.2 滑动窗口算法设计
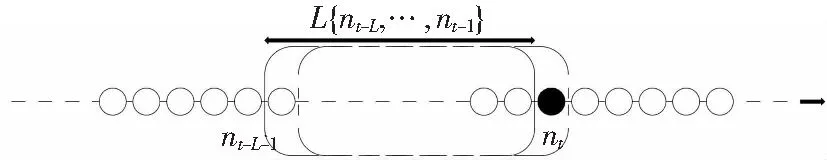

2.3 动态参数设置算法设计
3 实验仿真
3.1 数据与仿真环境
3.2 时间性能分析
3.3 相关性验证与计算
3.4 综合性能分析


4 结论

