基于范数加权的二维主成分分析提取图像特征

胡卫强，周浩，汪祥

(南昌大学数学系，江西 南昌 330031)

近些年来，图像特征提取在图像分类和识别方面有着越来越广泛的应用，引起了越来越多的研究人员的关注。而其中基于向量的特征提取方法尤其受到学者们的青睐，包括主成分分析法(principal component analysis，PCA)[1]、线性判别分析法(linear discriminant analysis)[2]、局部保持投影法(locality preserving projection)[3]，以及稀疏保持投影法(sparsity preserving projection)[4]等。尽管基于向量的特征提取方法如PCA已经成功应用于许多实际图像分类和识别等领域。但是，它的前提是需要将图像矩阵拉伸成一维长向量，由此导致一些图像的空间结构信息会丢失。

因此，为了充分利用图像的空间结构信息，许多基于矩阵的特征提取方法被提出，例如最早期的二维主成分分析法[5]、二维线性判别分析法[6]，以及二维局部保持投影法[7]等。这些方法与基于向量的特征提取方法不同之处在于它们的思想是直接针对二维图像矩阵处理，而无需将其拉伸为一维向量。上述算法中大多是基于L2范数或Frobenius范数，其中二维主成分分析方法是基于L2范数。

近几年来，Schatten-P范数在机器学习和模式识别领域引起了广泛的关注。例如Nie等[8]提出了一种基于Schatten-P范数最小化的低秩矩阵恢复方法来恢复低秩矩阵，并诱导出了一种有效解决基于Schatten-P范数的优化问题的算法。紧接着又提出了一类用于图像分类的Schatten-P范数基矩阵回归模型[9]。而Du等[10]提出了基于Schatten-P范数标准对图像的特征进行提取和分类。此外，Nuclear范数在图像恢复领域也得到了极大关注，因此利用Nuclear范数作为标准的二维主成分分析方法相继被提出[11]。

以上研究利用不同范数标准提取图像特征，但并未考虑范数加权来提取图像特征。因此，本文提出一种基于Nuclear范数和Frobenius范数加权的二维主成分分析方法(记为NF-2DPCA)来解决图像特征提取问题。另外还给出一类快速的迭代算法来求解NF-2DPCA中优化问题，并利用数值例子来验证新方法的有效性。

1 二维主成分分析(2DPCA)

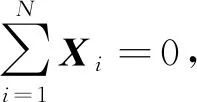
1.1 基于Frobenius范数的2DPCA

Frobenius范数2DPCA的目标函数为使得图像重构误差最小化，即

(1)

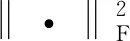
恒成立。因此式(1)可重写为

(2)

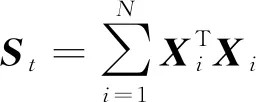
L=tr(VTStV)+λ(Ik-VTV)

(3)

式(3)对V求偏导可得

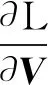
(4)

令式(4)为0，可得到StV=λV，代入式(2)，最后目标函数求解问题则转变为求解图像协方差矩阵前k个最大特征值对应的特征向量问题。

1.2 基于Nuclear范数的2DPCA

Nuclear范数2DPCA的目标函数度量准则如下

(5)

其中‖·‖*代表Nuclear范数，Nuclear范数定义为矩阵所有奇异值的和。并且对于任意矩阵A∈Rp×q，Nuclear范数与Frobenius范数之间转换有如下等式成立[11]

(6)

利用式(6)将目标函数(5)改写为

(7)

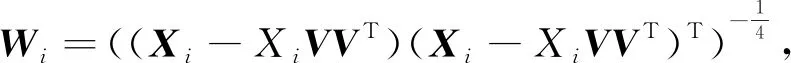
(8)

令V=Vk+1，更新Wi

那么关键的步骤即解决优化问题式(8)。式(8)的目标函数可重写为如下形式

(9)

(10)

实际上式(10)等价于式(8)，它的求解与式(2)方法一样，即求解矩阵D前k个最大特征值对应的特征向量。

2 NF-2DPCA

Frobenius和Nuclear均为Du等[10]提出的基于Schatten-P范数二维主成分分析(2DPCA-Sp)方法的特殊情形，其中矩阵A∈Rn×m的Schatten-P范数p∈(0,+∞)定义如下:

式中：σi代表矩阵A的第i个奇异值。容易看出，Nuclear范数和Frobenius范数分别是p=1和p=2的Schatten-P范数的特例。2DPCA-Sp目标函数为如下形式

(11)

本文受到Schatten-P范数2DPCA的启发而提出NF-2DPCA。令Xi∈Rm×n(i=1,2,3，…,N)为N张训练图像矩阵，不失一般性，假设图像矩阵均已中心化。提出的范数加权二维主成分分析算法旨在寻找最优投影矩阵V=[v1,v2,…,vk]∈Rn×k使得特征空间中特征总散射最大化，即目标函数为如下形式

(12)

式中：α为加权系数。由上节内容可知，式(12)为Frobenius范数与Nuclear范数的加权目标函数。接下来对式(12)进行求解。

为了求解优化问题式(12)，首先构造式(12)的拉格朗日函数

其中S∈Rk×k，是对称拉格朗日数乘矩阵。由微分性质有

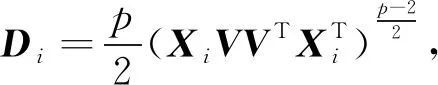
(13)

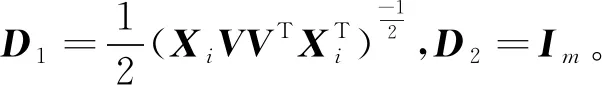
由式(13)可得

MV=VS

可以验证M是一个对称矩阵。可通过对M进行特征分解或者谱分解找到满足方程的列正交矩阵V。现求解最大化式(12)，即求解M的前k个最大特征值对应的特征向量V。

基于上述分析与观察，本文提出一个快速迭代算法求解优化问题(12)，完整的算法在算法1中给出。

算法1

输入：N张训练图像矩阵Xi∈Rm×n(i=1,2,3，…,N)且中心化,加权系数α,主成分k

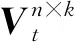
(2)While‖Vt+1-Vt‖>ε或t<100

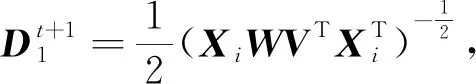
(4)对Mt+1执行特征分解,并获得Vt+1为Mt+1的前k个最大特征值对应的特征向量

(5)检查收敛条件‖Vt+1-Vt‖<ε或t>100

(6)t←t+1

(7)end while

输出:投影矩阵V

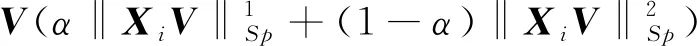
t

3 实验部分

在3个流行的图像数据库上进行实验，包括ORL数据库、Yalefaces数据库和AR数据库，以评估提出的范数加权2DPCA在图像特征提取方面的性能。在实验之前，将所有人脸图像调整到64×64像素。并且所有实验中k的最大值设定为50。此外，由于提出的范数加权2DPCA是一种无监督方法，本文仅将其与几种最先进的无监督方法进行比较，包括2DPCA[5]，OMF-2DPCA[12]，l2,p-2DPCA[13]使用最近邻分类器进行分类，之后通过识别精度来评估这些方法的性能。在本次实验中设置算法终止条件为最大迭代次数100或‖Vt+1-Vt‖F<10-4。实验代码在Python 3.7.9上编写。运行环境为PC 2.30 GHz CPU处理器、12.0 GB内存和Windows 10操作系统。

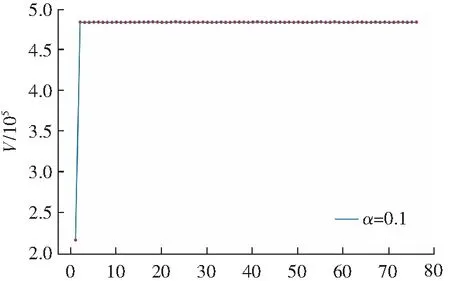
实验一采用来自于耶鲁人脸数据库的素材，该数据库包含15个人在不同面部表情和光照条件下的165张图像(每个人有11张不同的图像)。随机将165张图像分成4:1的训练图像和测试图像，并随机选取一张照片进行人脸重构，重构人脸如图2所示。此外选取主成分k，从5开始，每次递增5，直至50，加权系数α为0.1对图像利用最近邻识别分类，所有的实验均重复做10次，结果取10次的平均值，识别率(准确率)η如表1所示。

从图2中可以发现，随着主成分k递增，重构图像逐渐清晰，可反映出计算的投影矩阵V有效，因此进行下一步人脸识别。从表1可知当主成分k取到15，25，40，45，50时提出的算法识别率η是高于其他三种方法，尤其在k=15时算法识别准确率超过80%，而其他方法均未超过80%，进一步说明模型优于其余方法。

图2 k=5,10,…,50时重构人脸

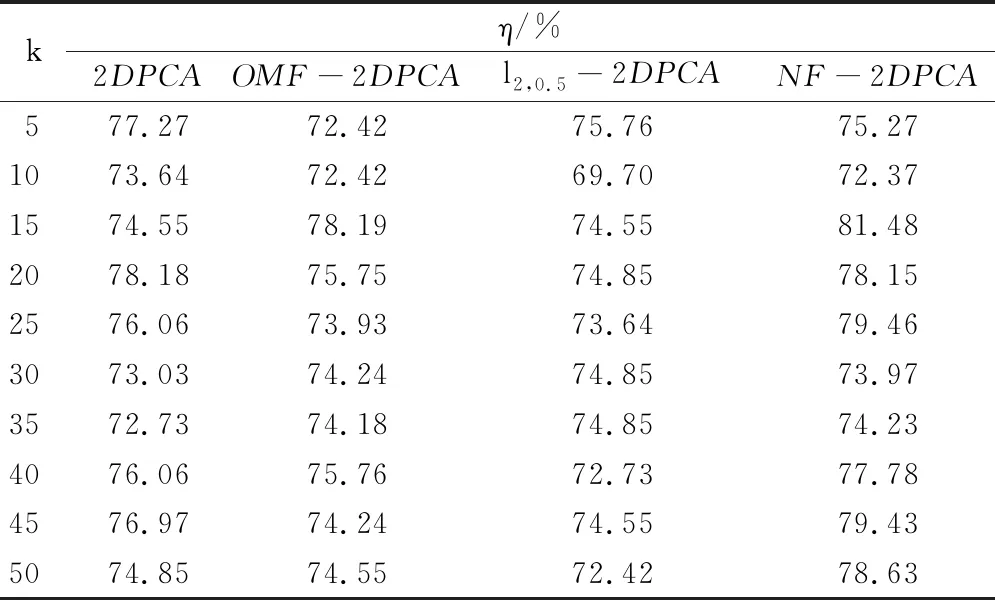
表1 Yalefaces识别准确率

实验二采用来自于ORL人脸数据库的素材，ORL人脸数据库包含40个不同对象的400幅图像。每人均有10幅不同种类的图像，如面部表情、不同的照明和面部细节(戴眼镜与否)。实验随机将400张图像分成4:1的训练图像和测试图像，并随机选取一张照片进行人脸重构，重构人脸如图3所示。接着利用最近邻算法对图像进行分类，所得到的识别率如表2所示。

图3 k=5,10,…,50时重构人脸

从图3中可以看出，重构图像逐渐清晰，可反映出投影矩阵V的有效性，因此进行下一步人脸识别。观察表2发现基本所有算法准确率η都大于90%，主要原因取决于图像性质好，比如图像的色调、饱和度、明度、对比度、白平衡以及噪声等[14]。但提出的算法最终识别准确率在k取5，10，15，25，40，45，50时均优于其他算法，进一步说明算法的优越性。

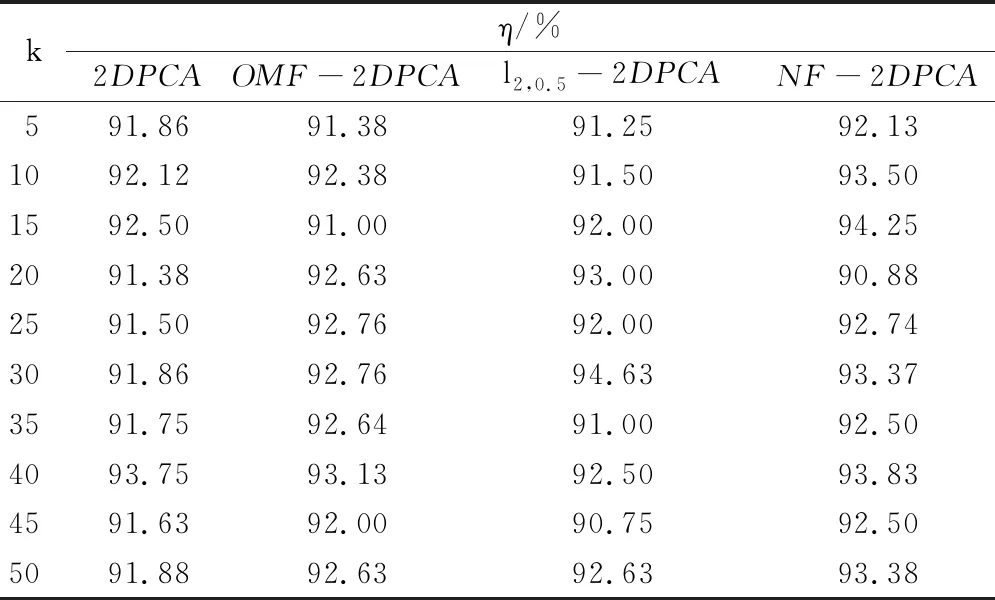
表2 ORL识别准确率

实验三采用AR人脸数据库的素材，AR人脸数据库包含4 000多幅彩色图像，这些图像分别从126人(70名男性和56名女性)的正面视角下采集。另外这些照片是在两个时段拍摄的，并且每个人间隔两周。每个时段包含13张图像，其中7张图像具有不同的面部表情和照明条件，6张图像被眼镜和围巾遮挡。在实验中，选择了100人(男性50名和女性50名)的2 600张照片作为实验图像，每张图片被裁剪成120×120像素大小。随机选择80%图像用于训练，其余20%图像用于测试。另外随机选取一张照片进行人脸重构，重构人脸如图4所示。其中主成分k和加权系数α与前两个实验选择方式一样，所得到的结果如表3所示。

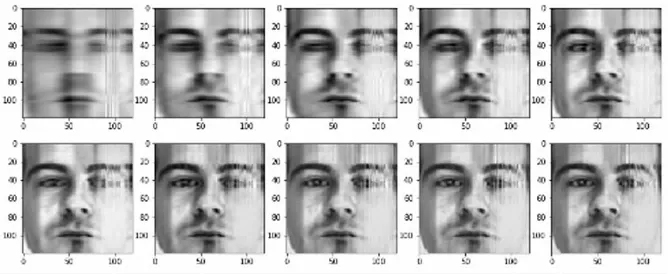
图4 k=5,10,…，50时重构人脸

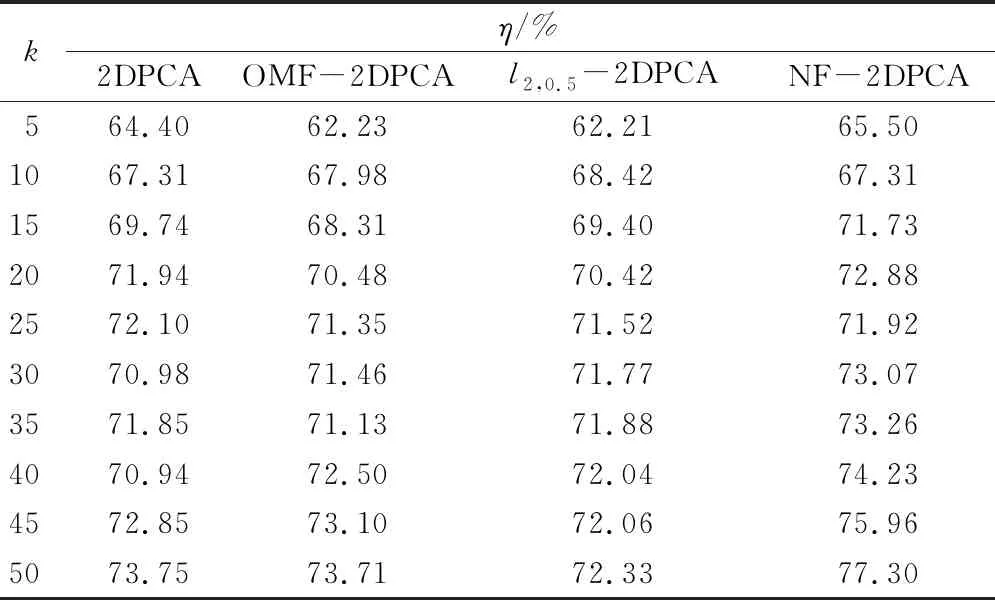
表3 AR识别准确率

从图4中可以发现，随着主成分k递增，重构图像逐渐清晰，从这反映投影矩阵V有效，因此进行下一步人脸识别。从表3可知，基本所有算法识别准确率都比前两个数据库中实验准确率低，原因在于实验图像数量远多于前两个人脸数据库。但所提出的算法在大部分情况下还是优于其他3种方法，进一步说明模型优于其余模型。

4 结论

(1) 所提出的NF-2DPCA方法对于图像识别最佳识别准确率能达到94.25%，显示所提出的模型加权思想有意义且效果更优越。

(2) 算法加权系数α可以取不同的值，当取值为多少时能使实验结果达到最优有待进一步去研究。