面向城市路网拥堵管理的区域停车收费协同定价优化方法

王 建，朱森来，陆丽丽，刘启超

（1.东南大学交通学院,江苏 南京 210096；2.南通大学交通与土木工程学院，江苏 南通 226019；3.宁波大学海运学院，浙江 宁波 315211）

引 言

随着私家车保有量的增加，城市中私家车的出行日剧增多，城市交通拥堵问题越演越烈。伴随着严峻的交通拥堵问题，近些年城市中的停车难问题也同样制约着很多城市的发展，不管是老城区还是新城区，由于交通需求过大、停车空间有限、管理设施匮乏等种种原因，不同区域的停车问题呈现出不同的特征。

针对交通拥堵，国内外许多城市提出众多控制策略，如工作时间的优化［1-2］，基于出行链的控制策略［3-4］，通过其他交通方式进行控制协调［5-7］，限速［8］等控制措施。这些策略通过增加私家车的出行成本或提高其他绿色出行方式的舒适性、便捷性等从而减少私家车的使用。在这些策略中，拥挤收费受到国内外最广泛的研究和关注［9-11］。拥挤收费属于经济杠杆策略，理论上对缓解交通拥堵有着良好的效果，然而由于社会公平性、出行者接受度不高等原因，拥挤收费在很多国家很多地区并未得到有效实施。同样作为经济杠杆策略，针对停车问题，停车收费策略［12-15］不仅得到国内外研究者的关注，在实际中也得到广泛应用。相比于对路段进行拥堵收费，对停车进行收费，社会公平性问题并不突出，出行者接受度会更高。停车收费的制定可以影响出行者出行方式的选择，合理的停车收费价格可以调节私家车出行比例，达到缓解交通拥堵的目的。

目前，城市各区域停车价格主要由供需关系，土地价格，城市居民收入等因素综合确定［16-18］。停车收费策略的主要目标是确定合理的停车收费价格促使出行者由私家车向公共交通或停车换乘方式转换。针对此目标，张兆芬［19］和徐丹丹［20］分别基于用户效用理论和前景理论构建出行者方式选择模型，分析停车收费对私家车出行和公共交通出行两种交通方式分担率的影响；曹弋等［21］构建并拟合包含地铁、公交、小汽车及停车换乘（小汽车+地铁）四个选择肢的Logit模型，通过调整不同区域的停车收费价格，得到停车费用与停车换乘及全程小汽车出行比例的关系；Wang等［22］提出一种基于混合整数规划的最优停车收费模型，通过优化停车场预留给不同起始点车辆的停车位个数及其价格来提高出行者采用停车换乘方式出行的比例；Acierno等［23］假设停车场可以根据出行起始点的不同收取不同的费用，提出一种基于方式选择-起讫点出行需求分布的组合优化模型，模型通过调控不同起讫点车辆的停车费用优化出行方式结构，促使起讫点间有地铁连接的出行者尽可能采用地铁出行。

综合考虑治理交通拥堵和制定停车收费策略，有部分学者把停车收费作为一种缓解交通拥堵的手段进行分析研究［24-26］。这些方法通常基于用户均衡理论解析停车收费对出行者出行行为的影响机理，采用交通分配模型预测不同停车收费策略对交通网络流分布的影响。尽管上述研究都已注意到停车收费作为经济杠杆在缓解交通拥堵方面的作用，但侧重点主要是通过停车收费促使私家车出行者尽可能向公共交通或者停车换乘方式转变，从而间接达到缓解交通拥堵的目标。我们依然缺少合理有效的方法量化停车收费价格对城市各区域间交通出行需求和道路网络流量的影响，因此，我们并不能有效评估和预测停车收费价格对缓解交通拥堵方面作用与效果，从而限制了相关政策的有效推行和实施。

针对以上不足，本文考虑停车收费对出行者选择私家车出行的影响，综合考虑出行需求受停车收费和出行时间影响的弹性特征，构建面向网络流量预测的弹性需求下用户均衡交通分配模型；接着，为调控交通网络时空出行需求，提高交通网络的运行效能，将该模型作为下层模型，构建了停车收费区域协同双层优化模型，并设计相应的求解算法，证明了算法的收敛性；最后，通过案例分析验证模型及算法的可行性和有效性。

1 区域停车收费协同定价优化方法

1.1 面向路网流量分布预测的交通分配模型

为了评估各交通小区停车收费对缓解交通拥堵的效益以及网络运行状况的影响，需要对停车收费实施后道路网络各路段流量进行预测。因此，首先研究停车收费价格给定的条件下路网流量分布预测方法。

停车收费会影响出行者的出行选择行为，出行需求存在很大的弹性。传统的考虑弹性需求的交通分配模型往往只考虑了出行需求弹性与起讫点出行时间的关系。在实际情形中，部分交通小区实施停车收费策略之后也也会降低去往这些小区的交通需求，为反映该现象，基于文献［27］，本文综合考虑出行时间和停车收费对出行需求的影响，当出行终点所在交通小区s收取停车费用时，从交通小区r到交通小区s的实际出行需求函数定义为：

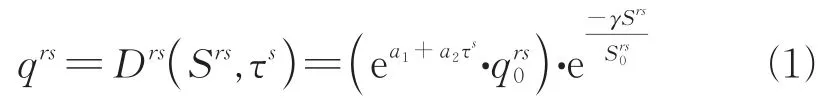
式中qrs为交通小区r到交通小区s的实际出行需求；为交通小区r到交通小区s的出行总需求；Srs为交通小区r到交通小区s之间有流量的路径的实际平均行驶时间；τs为交通小区s收取的停车费用；Drs(Srs，τs)和Drs(Srs)为交通小区r到交通小区s的实际出行需求函数；为自由流状态下交通小区r到交通小区s间最短出行时间；a1和a2是反映停车收费对出行需求影响的相关系数，实际应用时可以通过SP调查数据进行拟合标定，具体步骤可以参见本文案例研究，之所以定义两个与停车收费相关的参数，是为了能更好地拟合实际调查数据；γ为反映出行时间对出行需求影响的相关系数。

基于式（1），为预测道路网络流量分布，假设出行者都以使得私人出行时间最小化为原则选择出行路径，本文构建弹性需求下用户均衡交通分配模型如下：

式中A为城市道路网络所有路段的集合；Sτ为所有设置停车收费交通小区的集合；为交通小区r到交通小区s间第k条路径流量；为路径-路段关联变量，如果交通小区对rs间第k条路径经过路段a，，否则，是Drs(Srs，τs)关于Srs的反函数；是Drs(Srs)的反函数；Rrs是OD对rs间所有路径的集合。

式（2）是目标函数，反应了出行者以私人出行效用最大化为原则选择出行路径，同时反应出行需求受停车收费和出行时间影响的弹性特征；式（6）是路段流量与路径流量的守恒约束；式（7）是OD需求与路径流量的守恒约束；式（8）是流量的非负约束。该优化问题（2）～（8）的最优解和(qrs*，∀rs)是唯一的［26］。在均衡状态下，起讫点之间有流量的路径其行驶时间都相等，因此Srs即为交通小区对rs间有流量的路径的行驶时间。弹性需求下用户均衡交通分配模型求解方法可见文献［28-29］。

1.2 区域停车收费协同定价双层优化模型

停车收费不仅可以影响停车收费区域周边道路交通流量，有效调控道路拥挤程度，也会影响整个道路网络流量的分布，改变道路网络交通运行状态。因此，停车收费优化的目标不仅仅是减小当前局部地区道路拥挤程度，也要考虑停车收费对道路网络交通流量分布和运行状态的影响。

本文采用路网用户总盈余量化停车收费对道路网络运行状态的影响，在交通出行网络中，用户盈余是道路网络所有出行者为了到达终点愿意付出的时间成本与实际支付的时间成本之差［29］，表示为：

根据式（9），构建区域停车收费协同双层优化模型，其中上层模型为：

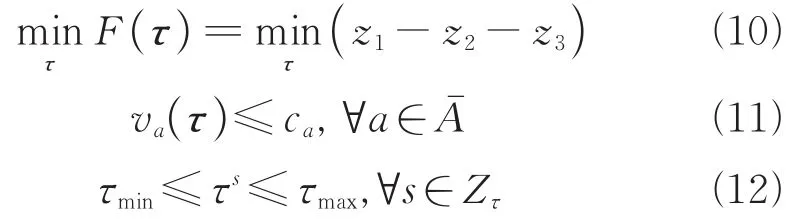
下层模型为前面构建的弹性需求下用户均衡交通分配问题（2）～（8）。

式（10）～（12）中，τ=[τs，∀s∈Zτ]，为当前拥挤路段的集合；ca为路段a的通行能力；τmin和τmax分别为τs的上下界。va和qrs的值通过求解下层弹性需求下用户均衡分配问题（2）～（8）所得。目标函数（9）是优化交通小区停车收费提高路网用户总盈余。约束条件（11）确保了设置停车收费价格后当前拥挤路段的流量不会超过相应的路段容量，从而解决了这些路段的交通拥堵问题。约束条件（12）中，τmin和τmax分别为τs设定的上下界。

2 求解算法

2.1 改进型可行方向法

1.2节所构建的停车收费双层优化问题是一个非线性优化模型嵌入另外一个非线性优化模型，该问题求解较难，传统求解双层优化问题多采用启发式算法，如遗传算法［30］、模拟退火算法［31］、基于敏感性分析的算法［32-33］等。这些算法收敛速度较慢且算法的收敛性无法保证，本文在Cawood等［34］研究成果的基础上，创造性地提出一种改进型可行方向法求解双层优化问题。

假设在第n次循环，当前各交通小区停车收费价格为τn，τn满足不等式（11）和（12），那么各交通子区停车收费价格可行方向dn可以通过求解如下二次凸优化问题获得：

式中ϑ为优化变量；－∇τF(τn)为－F(τ)在τn处对停车价格向量变量τ的梯度；∇τva(τn)为各交通子区停车收费价格为τn条件下路段a的均衡流量对τ的梯度；H为任意一个正定对称矩阵；σ为系数，σ＞0。

不等式（15）～（17）是不等式（11）和（12）在点τn处的一阶泰勒展开式；不等式（13）确保dn是－F(τn)下降方向。假设(ϑ*，dn)是上述二次凸优化问题的解，并且ϑ*＜0，则根据不等式（16），当α充分小时，－F(τn+αdn)＜－F(τn)，且在τn+αdn满足不等式（11）和（12），即dn是目标函数F(τ)在τn点处的可行下降方向。

因此，求解分区域停车收费双层优化问题的改进型可行方向法流程如下：

步骤0：设n=1，设置初始停车收费价格τn，τn满足不等式（11）和（12），将τn带入下层弹性需求下用户均衡分配问题，求解停车收费价格τn条件下道路网络均衡流量、OD需求量以及对应的路网用户总盈余（即F(τn)）。

步骤1：求解二次凸优化问题（13）～（17）获得τn处可行下降方向dn。

步骤2：根据如下方法求解最优步长α：取一个充分小的初始值α0，求解最大整数h使得－F(τn+1.618hα0dn)＜－F(τn)，并且τn+1.618hα0dn满足不等式（11）和（12）。

步骤3：设τn+1=τn+1.618hα0dn，如果‖F(τn+1)－F(τn)‖＜ϵ，ϵ为收敛标准，则停止循环，输出τn，否则n=n+1，返回第二步。

为了分析上述算法的收敛性，引用如下定理：

定理 1［29］：假设(ϑ*，dn)是二次凸优化问题（13）～（17）在τn处的解，并且τn不是构建的双层优化问题的解，那么我们必然有ϑ*＜0，且dn是τn处的可行下降方向。

定理2：改进型可行方向法是全局收敛的，即给定任意可行初始点τ1，上述算法一定会收敛到构建的双层优化问题的一个局部最优解。

需要注意的是，为了加快收敛速度，正定对称阵H一般设为单位矩阵，σ的取值一般为0.5～10之间。

2.2 ∇τF(τn)和∇τva(τn)，∀a的解析模型

在二次凸优化问题（13）～（17）中，F(τn)和va(τn)的值需要通过求解下层弹性需求下用户均衡分配问题获取，因此，∇τF(τn)和∇τva(τn)，∀a的值是未知的，为了求解该优化问题，本文采用弹性需求下用户均衡敏感性方法［36］计算∇τF(τn)和∇τva(τn)，∀a，具体过程如下：

假设f是弹性需求下用户均衡分配问题在τn处的一个路径解，则根据KKT条件，存在一个解f，π和u满足下列方程：

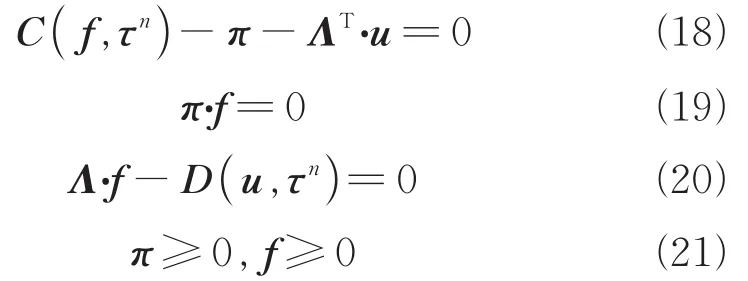
式中C(f，τn)为路径阻抗函数向量；u=[urs，∀rs]为流量守恒约束的拉氏乘子向量（也是UE均衡状态下OD对之间最小路径出行时间，此时有，Srs=urs）；π为非负路径流量约束的拉氏乘子向量；Λ是路径-OD对关联向量；D(u，τn)为所有的OD需求函数向量。由于只需考虑取值为正的路径流量中的非退化极值点时，因此上述方程组中主动约束条件可以删除，上述方程简化为：

式中 上标0代表相应的减少了行或列的向量及矩阵，上述受限制的方程（22），（23）满足了变分不等式的灵敏度分析所要求的全部条件，并且灵敏度分析的结果与所选择的极值点无关，当Δλ=0时，公式（22），（23）对(c0，u)的雅克比矩阵为：

由路段与路径之间的关系可得：

式中v为所有路段流量向量，Δ°是路段-路径关联矩阵。根据式（22），可得：

3 案例分析

3.1 背景介绍

为验证本文提出的区域停车收费协同定价优化模型及其算法的有效性和实用性，本文以美国Sioux Falls市局部地区为例，收集了该市道路网络较为详实的数据，包括居民出行需求数据以及道路网络信息。该网络作为典型的交通网络被国内外学者广泛应用于网络建模与验证研究中［27］。该市的道路网络如图1所示。为便于分析，将道路上相邻节点（交叉口）所围合成的区域称之为交通小区，如交通小区A是指由节点1，2，3，4所围合成的区域。

本文假设每个交通小区内部的停车位价格都是相等的，但是各交通小区之间的停车价格存在差异。当前，由于不断增长的交通需求，城市早高峰与晚高峰期间节点4与3、3与7以及7与6之间的路段存在严重的交通拥堵（如图1中红色路段所示），导致大量的交通延误，影响行车效率，对周边居民也产生很大的噪声污染。据调查，这些拥堵路段的交通流量大多是以交通小区A，B，C，D为终点。鉴于当前这些小区的公共停车位都是免费的，本文考虑对交通小区A，B，C，D四个交通小区的公共停车位在高峰时段收取停车费用，通过停车收费价格的设置从时空上调控交通需求，从而达到缓解道路拥堵的目的。

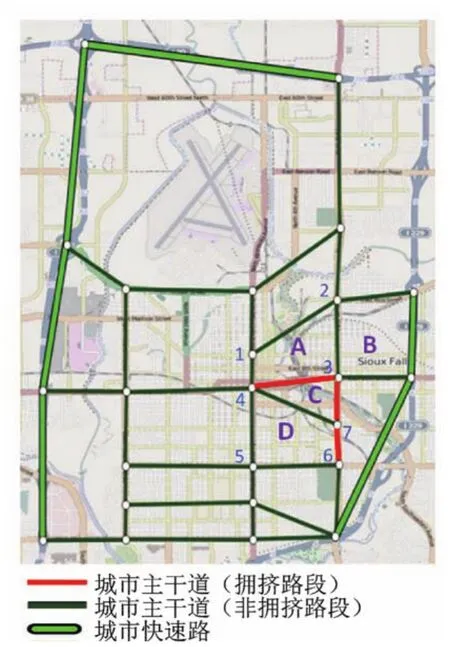
图1 Sioux Falls城市道路网络和收费区域示意图

为便于分析，将图1所示的道路网络转化为如图2所示的等价交通网络。该路网包含24个节点（交叉口），76条路段，其中交通小区A，B，C，D以及当前拥挤路段的位置如图2所示（加粗线条）。

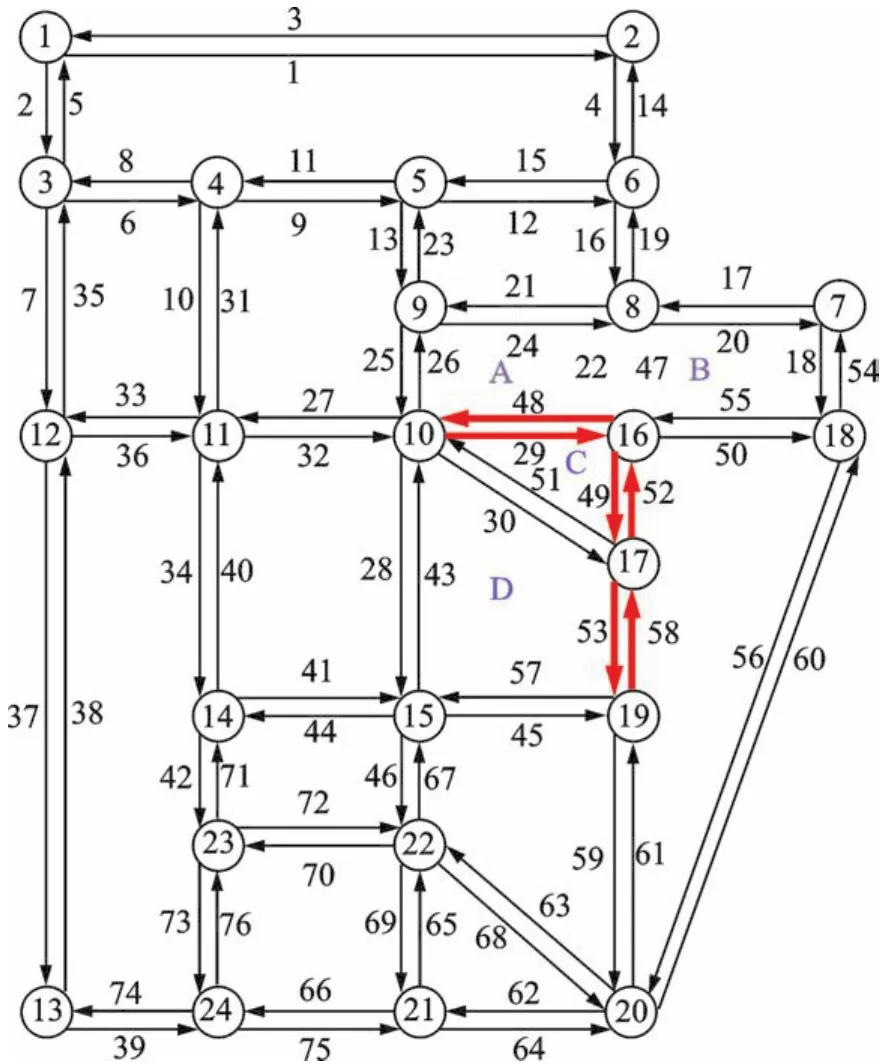
图2 Sioux Falls路网

已有的OD需求数据是该路网各个节点间的出行需求，而停车收费时针对小区进行收费的，而不是对节点进行收费，为反应交通小区收费对节点之间需求的影响，假设去往某个节点的出行需求量最终去往其临接的交通小区概率是相等的，各交通小区的停车收费会影响与其相关的这部分出行需求。以图2所示的路网中节点16为例，与该节点相连的交通小区有四个，包括所考虑得交通小区A，B，C，假设从节点1到节点16的原始出行需求为100，那么根据假设去往各相邻交通小区的需求分别都为25（即式（1）中的），当交通小区A，B，C实行停车收费时，根据式（1）去预测受停车影响之后的相关需求变化，最后再累加推算出OD对1～16受相邻交通小区停车收费影响的出行需求。

为了体现交通拥堵的规律，本文将道路行驶时间定义为关于路段流量的递增函数，采用美国联邦公路局模型［28］预测道路行驶时间：

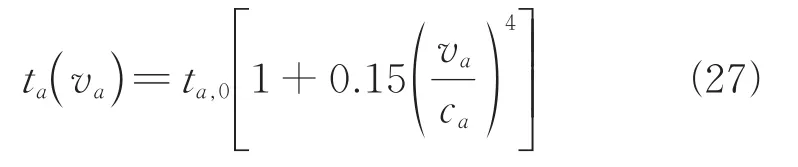
式中ta为路段a的行驶时间；ta，0为自由流状态下路段a的行驶时间；va为路段a的交通流量；ca为路段a的总容量。

采用流量/容量（volume/capacity，v/c）比来表示道路拥挤程度，当v/c远小于1时，道路处于非拥挤状态，当v/c远大于1时，道路处于超饱和状态，此时，交通拥挤现象严重。当前拥挤路段29，48，49，52，53和 58的v/c分别是 1.13，1.15，1.03，1.05，1.09和1.07，显而易见，这些路段的流量都处于超饱和状态，拥堵现象严重。

3.2 停车收费对私家车出行选择影响分析

为了缓解交通拥堵，采用本文提出的区域停车收费协同优化方法，首先，分析停车收费对私家车的出行选择影响，对式（1）中的系数a1和a2进行标定。本文采用网络SP调查问卷在Sioux Fall市进行数据搜集和分析。在该问卷中，有三个重要问题：一是“在工作或学习出行中，您主要的出行方式是什么”；二是“在购物/社交/娱乐出行中，您主要的出行方式是什么”；三是“出行者放弃私家车出行的停车收费临界价格是多少”。调查一共收集了343份有效问卷结果，其中，119人回复在前述两种出行活动中均不选用私家车出行，因此其调查结果作废，最后224份平常出行活动中会采用私家车出行的问卷结果可应用到本文中，这224个被调查者对于放弃私家车出行的临界停车收费价格汇总如图3所示。

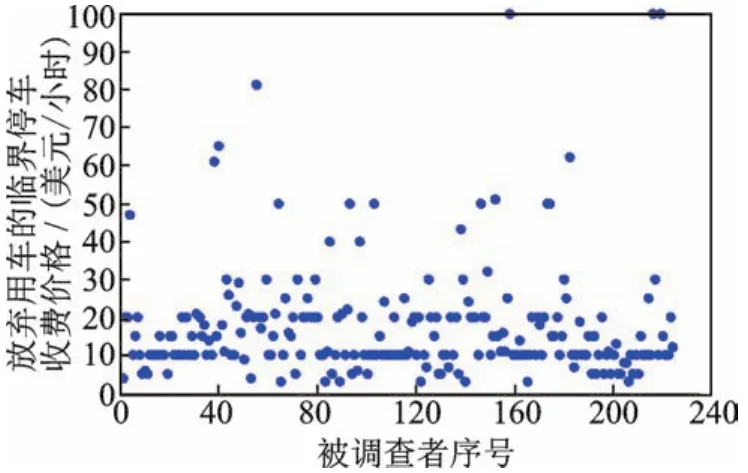
图3 放弃私家车出行的临界停车收费价格分布

由图3可知，大部分出行者放弃采用私家车出行的临界停车收费价格为10～20美元/小时。假设终点所在交通小区停车收费价格为τ美元/小时，根据图1，可以采用如下公式计算使用私家车去往该交通小区的出行人数比例（设为P(τ)）：

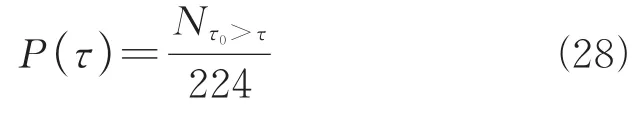
式中Nτ0＞τ为放弃用车出行临界停车收费价格大于τ美元/小时的人数，224为有效问卷个数。

如图4所示显示了调查者中继续用私家车出行的人数比例随着停车收费价格的变化特征，使用私家车出行的人数比例随着停车收费价格的增长而呈现指数级下降趋势，因此构建如下拟合函数：

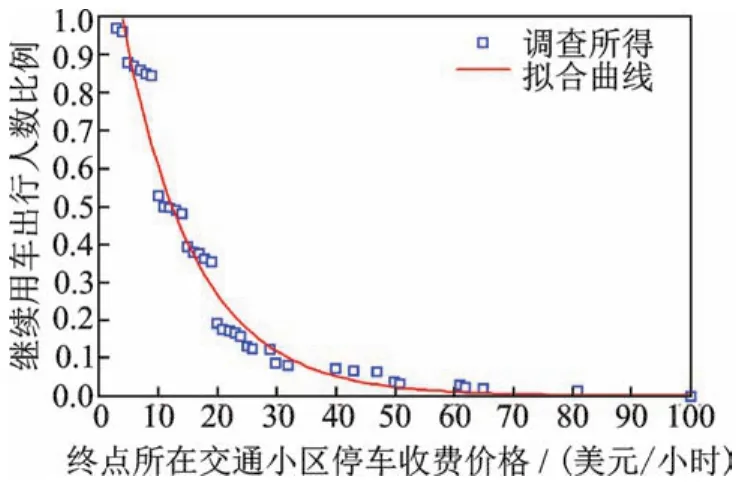
图4 继续用私家车出行的人数比例与停车收费价格的相关性分析

采用非线性最小二乘法，公式（29）中a1和a2最优拟合值分别为0.3219和－0.0819。由表2可知，拟合结果中和方差和均方差都较小，且确定系数很接近于1，因此拟合效果较好。

表2 拟合效果

3.3 最优停车收费定价计算

带入a1和a2的拟合值，采用构建的双层优化模型优化交通小区A，B，C，D的停车收费，调节交通出行需求，实现缓解道路拥堵以及提高道路网络用户盈余的目的。

设改进型可行方向法收敛标准ϵ=10－4。假设这四个交通小区初始停车收费价格都设为20美元/小时，表3给出了改进型可行方向法每次迭代所得各交通小区停车收费价格，图5给出了相应的目标函数迭代曲线，该曲线表明路网用户盈余（F(τ)）随着迭代次数的增加而增加，说明可行方向法是有效的；并且仅经过12次迭代就收敛到双层优化问题的最优解，因此其求解效率很高。

图5 改进型可行方向法迭代收敛曲线

从表3可知，当交通小区A，B，C，D对公共停车位价格分别设置为10.73美元/小时、4.52美元/小时、8.66美元/小时、6.76美元/小时时，道路网络用户总盈余最多，为2.435×106分钟。

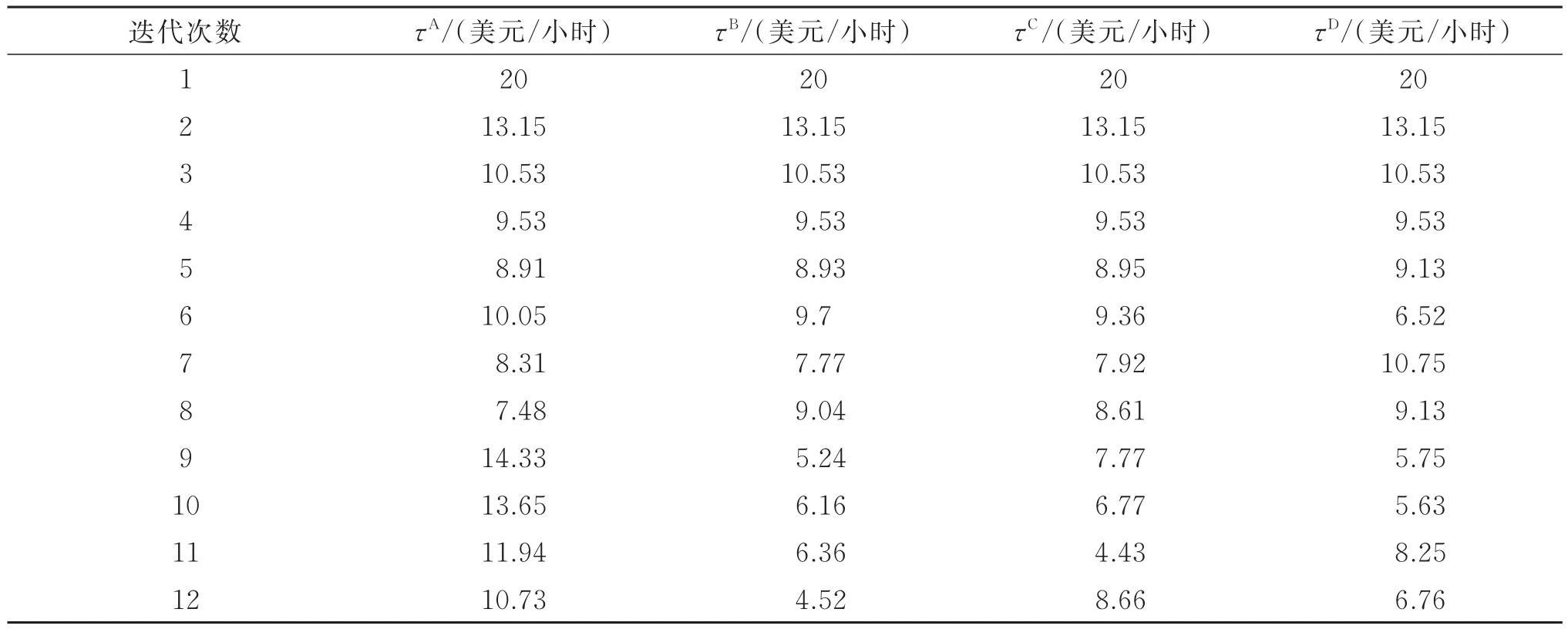
表3 改进型可行方向法每次迭代所得各交通小区停车收费价格

图6比较了停车收费价格优化前（无收费）和优化后各交通小区到达交通量。由图6可知，在最优收费价格条件下，以这四个交通小区为终点的到达交通量都有所降低，其中进入交通小区A的交通量降低了40%。表5给出了停车收费价格优化前后道路网络各路段流量容量比（v/c），结果表明通过设置和优化停车收费价格，当前拥挤路段29，48，49，52，53和58的流量容量比都小于1，这说明本文所提出的最优停车收费价格可以有效缓解道路网络交通拥堵问题。并且道路网络上其他路段流量容量比也较优化前（即无停车收费）都有所改善，因此本文所提出的停车收费优化策略不仅可以改善局部地区的交通拥堵，也能有效提高道路网络交通运行状况，具有很好的应用价值。

图6 停车收费价格优化前后各交通小区到达交通量

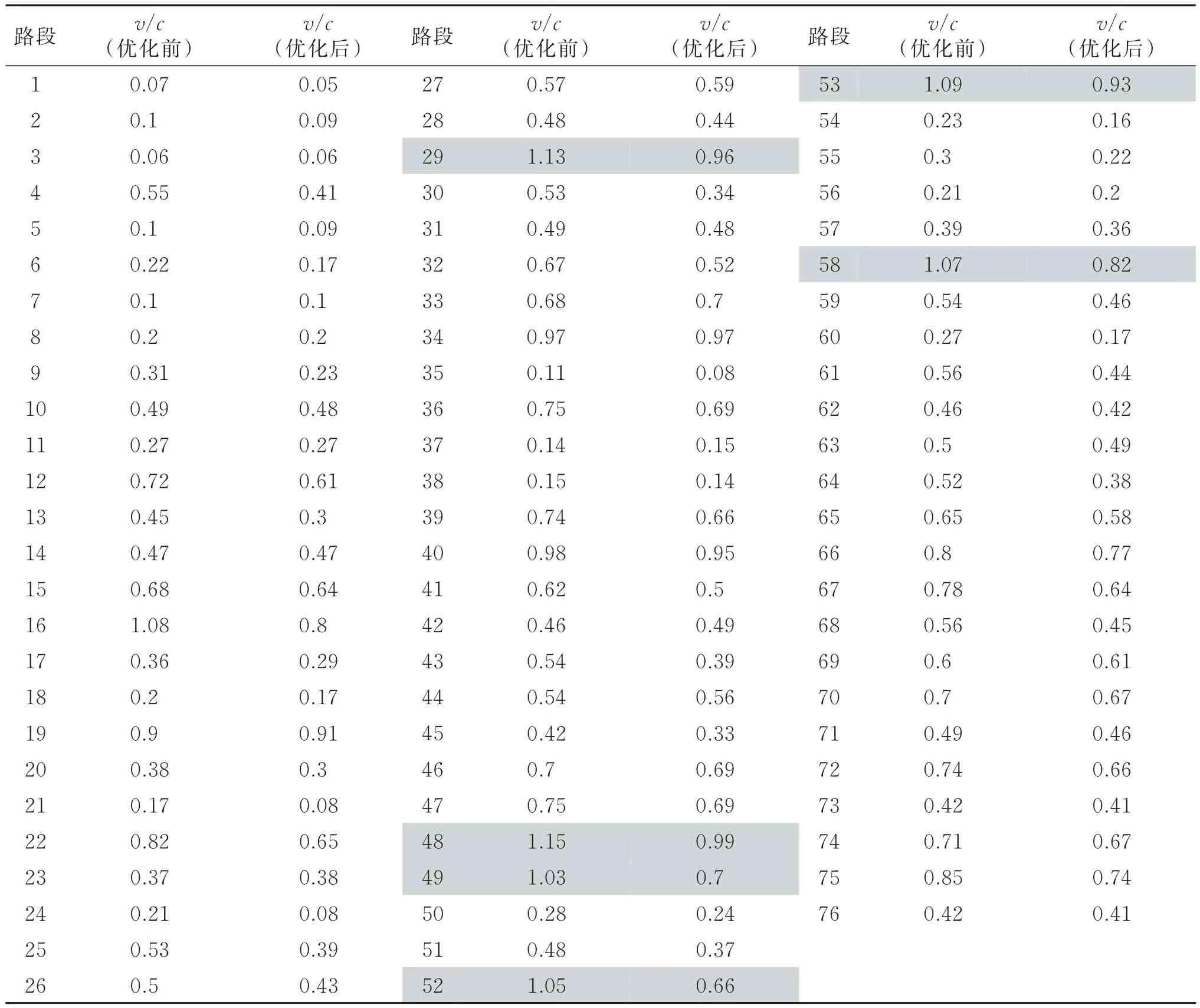
表4 停车收费价格优化前后道路网络各路段v/c

4 结束语

（1）实际情形中，出行需求存在很大的弹性，出行需求的弹性除了受出行时间成本的影响，同样也会受停车成本的影响。通过SP调查分析，私家车出行比例会随着停车收费价格的增长而呈现指数级下降趋势。

（2）综合考虑停车收费与出行时间对出行需求的影响，构建了弹性需求下的用户均衡分配模型，用于预测路网的流量分布。接着，将此模型作为下层模型，构建了停车收费区域协同双层优化模型，上层以提高路网用户总盈余为目标优化交通小区停车收费。为求解该双层优化问题，提出一种改进型可行方向求解算法，并证明了算法的全局收敛性。最后，通过数值分析验证了模型的可行性和有效性，同时证明了设计的算法拥有很好的计算效率。

（3）不同年龄、收入、工作性质等类型不同的出行者往往具有不同的时间价值成本和经济杠杆策略的敏感度，即出行者存在很大的异质性。本文构建的弹性需求下的用户均衡分配模型和停车收费区域协同双层优化模型并没有考虑出行者的异质性，后续的研究中将考虑出行者异质性，继续搜集更多样本数据分析停车收费对不同出行者的出行行为影响，并对用户均衡分配模型和停车收费优化模型进行扩展。

（4）本文提出的求解双层优化模型的算法被证明可以保证全局收敛性，但是不能保证得出的结果是全局最优解，未来会进一步改进算法保证算法既拥有全局收敛性又能得到全局最优解。另外，本文构建的停车收费区域协同双层优化模型只考虑了私家车的出行，未来需进一步融合各种交通方式，综合考虑方式选择和交通分配进行组合优化。