新冠疫苗接种的动态演化博弈分析

苏 然，廖慧敏，陈森林

（安庆师范大学 数理学院，安徽 安庆 246133）

2019新型冠状病毒（COVID-19）给人民的身体健康和正常生活造成了极大的伤害，接种新冠疫苗是行之有效的预防手段[1-2]。陈薇等[3]分析了研制新冠疫苗和推进疫苗接种面临的挑战，吴海等[4]探讨了影响疫苗接种的因素，Garvey等[5]论述了不同方式接种COVID-19疫苗的影响。本文以演化博弈论为理论依据，刻画政府和城乡居民在疫苗接种过程中的博弈策略。考虑博弈双方在疫苗接种过程中的联系，并在此基础上得到双方的收益矩阵，分析均衡点的稳定性。但在实际生活中，城乡居民参与疫苗接种的概率受“从众心理”影响，据此引入动态损失函数来刻画城乡居民拒绝接种疫苗所带来的损失。

1 新冠疫苗接种的演化博弈模型构建

假设在博弈过程中只有城乡居民和政府两类有限理性的博弈参与方，且疫苗接种后永久保持免疫效果。对已经研制成功且通过临床试验的新冠疫苗，城乡居民可选择接种，也可选择不接种，假设选择接种疫苗的概率为x，则选择不接种疫苗的概率为1-x。政府同样也有两种策略：积极推进、顺其自然，假设选择积极推进疫苗接种的概率为y，则选择顺其自然的概率为1-y。

假定P1是城乡居民接种疫苗的收益，如增强机体对病毒的免疫能力；P2是城乡居民的基础收益，包含城乡居民日常工作和生产经营的总收入；P0是城乡居民自觉接种疫苗时的额外收入，如降低被感染风险、进一步增强抵抗力等；C1是政府积极推进疫苗接种的成本，如宣传疫苗接种的广告投入成本、研制疫苗的资金投入成本等；C2是政府面临疫情扩散等的经济损失；P3是城乡居民接种疫苗，社会繁荣发展时的政府收益；P4是政府的基础收益，包括政府的税收收入等；B是政府积极推进疫苗接种，但城乡居民拒绝接种疫苗的损失；A是政府积极推进疫苗接种，但城乡居民不接种疫苗时的政府损失。根据模型假设，可以得到城乡居民和政府的收益矩阵，如表1所示。

表1 收益矩阵

城乡居民选择接种疫苗的期望收益为Ex，选择不接种疫苗的期望收益为E1-x，城乡居民以概率x选择接种疫苗，以概率1-x选择不接种疫苗的混合策略期望收益为，具体计算公式为

再将均衡点代入J中，求出均衡点对应的行列式和迹，结果如表2所示。

表2 均衡点对应矩阵的行列式和迹

2 模拟与分析

2.1 均衡点的稳定性

均衡点的稳定性取决于|J|和迹的正负[7]，|J|和迹的正负取决于收益矩阵中各参数的取值，见表3。由表3可知，在均衡点(x*,y*)处tr(J)=0，因此(x*,y*)不是系统演化的稳定点，故只需判断均衡点O、D、E、F的稳定性。城乡居民接种疫苗可以增强免疫能力，保证自身收益稳步上升，因此P1+P0＞P2。在此条件下，为便于分析，只需讨论B+P1-P2、C2-C1-A、C2-C1的正负。由表3可知，P1+P0-P2＞0时，（0，0）不是政府和城乡居民演化博弈的稳定点，即政府不采取具体措施且城乡居民不接种疫苗是永远不可能稳定存在的。由表3可知，当C2-C1-A＞0且P1+B-P2＜0时，即政府面临疫情扩散时的损失大于政府积极推进疫苗接种的成本，且城乡居民接种疫苗的收益小于不接种疫苗的收益，此时，（0，1）是城乡居民和政府演化博弈的稳定点。

表3 均衡点稳定性分析

设P0=0.5，P1+B-P2=-1，C2-C1-A=1，城乡居民接种疫苗的概率x和政府积极推进疫苗接种的概率y的初始取值均为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0，则博弈系统在不同初始概率下向稳定点（0，1）演化的过程如图1（a）所示。因为个体的免疫能力不同，接种疫苗后可能会产生不良反应，从而接种疫苗的收益P1小于不接种疫苗的收益P2，博弈系统将向（0，1）演化，即城乡居民选择拒绝接种疫苗。因此，为促进接种疫苗，政府应监管疫苗接种的安全性，降低疫苗接种的风险性。

由表3可知，当C2-C1＜0且P1+P0-P2＞0时，即政府积极推进疫苗接种的成本大于疫情扩散的损失，且城乡居民接种疫苗的收益大于不接种疫苗的收益，此时，城乡居民的最优策略是选择自觉接种疫苗，系统中所有的初始值经过一段时间的演化后都收敛于稳定点（1，0）。设B=2，P1+P0-P2=2，C2-C1=-1，A=1，根据上述分析，模拟得到博弈系统在不同初始概率下向稳定点（1，0）演化。接种疫苗增强了个体对病毒的免疫能力，有效降低了被感染的风险，城乡居民接种疫苗概率都向x=1演化，但由于政府的投入成本C1较大，导致博弈系统最后演化成如图1（b）所示，演化后都收敛于（1，0），即在政府不干预的情况下，所有城乡居民都自觉接种疫苗。

而且，当C2-C1＞0且P1+B-P2＞0时，即政府积极推进疫苗接种的成本远小于疫情扩散的损失，且城乡居民接种疫苗收益大于不接种疫苗收益时，（1，1）是稳定点。设B=2，P1-P2=1，C2-C1=2，P0=1，A=1，在这种情况下因政府大力推进疫苗接种且城乡居民积极参与，降低了城乡居民被病毒感染的风险，如图1（c）所示，系统向稳定点（1，1）演化，即政府积极推进疫苗接种时，城乡居民都自觉接种疫苗。

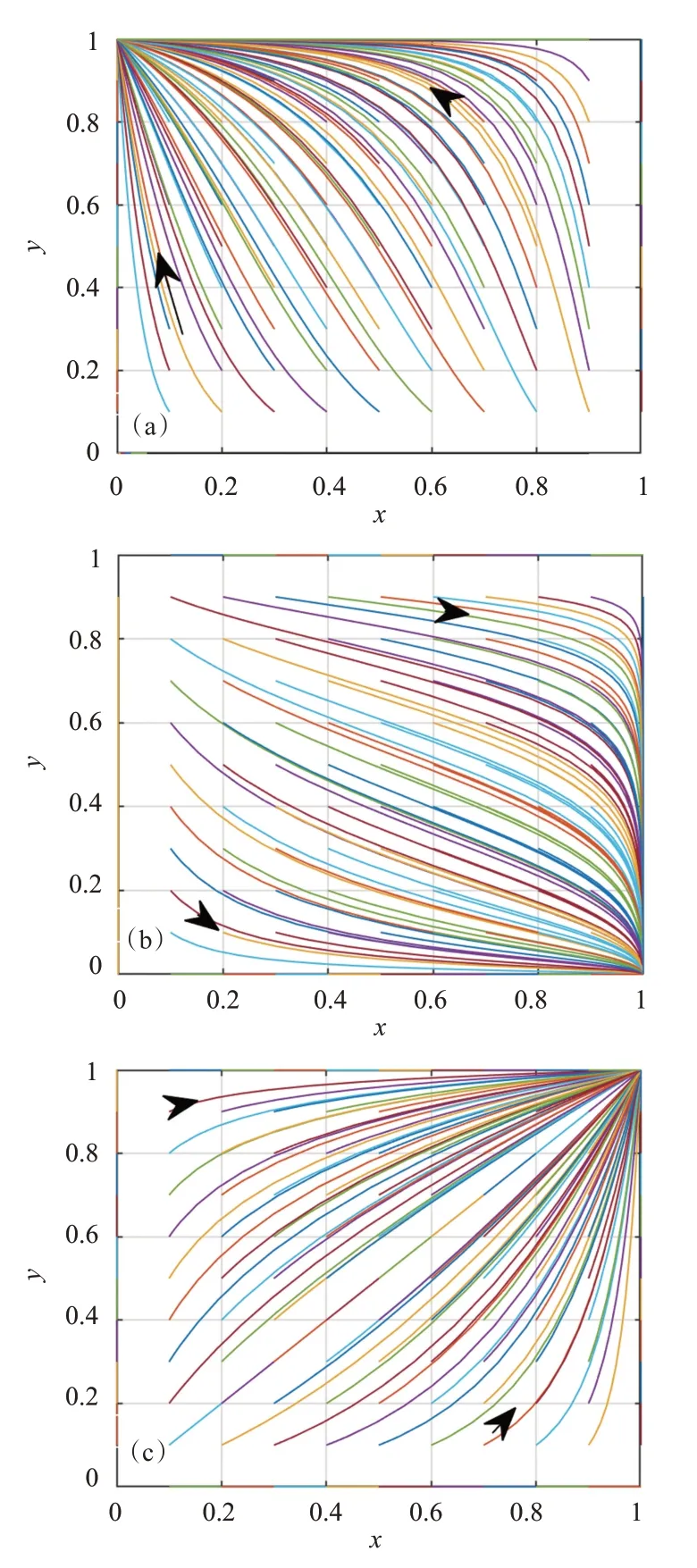
图1 博弈双方向稳定点演化的动态过程。（a）（0，1）；（b）（1，0）；（c）（1，1）

2.2 动态损失下的演化博弈分析

在前面的分析中，假设政府积极推进疫苗接种，但城乡居民考虑可能会产生不良反应拒绝接种疫苗时的损失B为固定值。然而，从实际情况来看，接种疫苗的概率和疫苗接种时的心理特征有关。城乡居民在疫苗接种的策略选择上，往往会出现“从众心理”，当个体周围选择接种疫苗的概率越大，个体选择接种疫苗的概率也随之上升[8-11]，反之，则不然。城乡居民拒绝接种疫苗的概率会影响其损失B，故考虑用对数损失函数B=log( )

1+e1-x来刻画拒绝接种疫苗时的动态损失[12-13]，将B代入式（3），得到复制动态方程为

下面对博弈系统的4个均衡点O（0，0），D（0，1），E（1，0），F（1，1）的稳定性进行分析，先求出该博弈过程的雅克比矩阵：

再将系统的均衡点代入J中，求出均衡点的行列式和迹，结果如表4所示。

表4 均衡点的行列式和迹

城乡居民接种疫苗后对病毒的免疫力有所增强，健康收益稳步上升，即P1+P0＞P2。此时，均衡点（0，0）的雅可比矩阵的行列式和迹均为正，所以（0，0）不是稳定点；考虑损失函数的取值范围恒为正，据表4可知均衡点（0，1）的雅可比矩阵的行列式恒为负，所以（0，1）不是稳定点。均衡点（1，0）满足演化稳定策略，但在实际生活中，疫情扩散造成的损失较大，C2作为政府面临疫情扩散时的经济损失大于政府积极推进疫苗接种过程中的成本C1，均衡点（1，0）的雅可比矩阵的行列式为负，所以（1，0）不是稳定点。均衡点（1，1）满足演化稳定策略，如图2所示，系统中所有的初始值经过一段时间的演化后都收敛于（1，1），即城乡居民选择接种疫苗的概率向x=1演化，而政府积极推进疫苗接种的概率向y=1演化，最终博弈系统向稳定点（1，1）演化。

图2 动态损失下博弈双方策略选择过程

综上所述，在引入动态损失函数的条件下，该系统仍具有稳定性。在实际情况中，随着“从众心理”的出现，越来越多的城乡居民积极接种疫苗，这表明政府积极推进疫苗接种、城乡居民积极参与接种疫苗会达到疫情防控最佳效果。

3 结束语

本文以演化博弈论为理论依据，构建新冠疫苗接种的演化博弈模型，阐述双方的收益矩阵，分析城乡居民和政府选择不同策略的演化过程，提出在有限理性条件下双方策略演化过程的复制动态方程。若要降低城乡居民被病毒感染的风险、增强机体对病毒的免疫能力，政府必须鼓励城乡居民积极参与疫苗接种。对于上述结论，给予两点建议：（1）政府在疫苗研制过程中应给予资金、人才和设备等方面的支持；相关部门应该严格把关疫苗研制过程的安全性，确保疫苗生产符合安全标准；（2）城乡居民应积极参与疫苗接种。