土压作用下面层弯矩和挠度计算方法研究
汪学清汪壮壮王建华
1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.深海矿产资源开发利用国家重点实验室,湖南长沙 410012
喷射混凝土施工是将混凝土在高压空气作用下高速喷向土层表面形成面层,对基坑边坡土体起临时保护和加固作用的一项基坑支护技术,具有工艺简单、施工灵活、快速高效等优点[1-3]。 随着经济的发展,该项技术在大量的地下工程中得到了广泛的应用。 虽然国内外对其已进行一些研究,但对面层的工作机理和受力分析的研究还比较少,没有形成一套较完整的理论体系。
面层的主要作用有承受水土压力、土钉、锚杆端部拉力、地面超载引起的荷载以及限制土体坍塌等,所以对面层的受力分析和设计非常重要。 现行规范中面层的施工和设计方法多采取经验方法,将面层设计按构造处理[4-6]。 德国有的工程按85%主动土压力设计永久支护面层,法国提出按土钉拉力30% ~40% 设计面层[7]。 王立峰等[8-9]把土钉墙面层简化为文克尔地基上的有限长梁,通过结构力学方法推导了土钉墙面层位移和内力的解析解,发现面层的位移和弯矩随基坑开挖深度的增加呈现出中间大两头小的分布特征。 杨茜等[10-11]针对止水帷幕与土钉联合支护技术,提出了可用无限长弹性地基梁模型分别对面层水平和竖直两个方向的横截面内力进行计算,并通过机动位移确定外力矩的分析方法推导了面层内力的计算公式。 季玉海[12]根据弹性梁理论推导出支护面层的计算公式,并通过实例对面层进行了强度验算和设计。 成峰等[13]在提出有效下滑力概念的前提下,结合增量法对滑楔平衡法进行改进,通过增量法+滑楔平衡法这种复合型算法计算得出土钉面层受力的结论,并与实测值进行了对比验证。 何江飞[14]基于弹性地基梁的理论将面层简化成钢筋混凝土板模型,通过混凝土结构设计原理计算钢筋混凝土板弯曲破坏和冲切破坏的极限承载力,推演出面层的受力情况,并利用有限元软件ADINA 建立面层、土体和土钉相互作用的模型,探讨了面层的作用机理,验证了所提出面层计算方法的正确性和合理性。赵勇[15]结合某微型桩复合土钉墙基坑支护工程,将面层简化为两对边简支的矩形板弯曲模型,计算了面层在土钉集中力和土体侧向压力共同作用下的弯矩和剪力。
上述文献中,有的将面层转化成弹性地基上的有限或无限长梁来考虑,这忽略了面层的整体性且推导的公式计算过于复杂,不宜工程使用;有的虽考虑了面层的整体性,将其简化成混凝土板,却仅仅提及了面层受力计算方法的理论依据,没给出实际工程面层设计所需的一般公式。 本文针对喷射混凝土这种基坑支护形式,研究支护面层在后方土压作用下的内力和变形的计算方法。 基于薄板小挠度弯曲理论和一定的假设条件及边界条件,推导了适合实际工程计算面层挠度的简单公式,以及面层的横向弯矩和纵向弯矩一般公式。 运用推导的公式计算某基坑工程中面层的挠度值和弯矩值,并将理论计算值与FLAC3D数值模拟值进行比较,验证了该公式的有效性,为类似基坑工程面层的设计提供借鉴。
1 薄板弯曲理论
板厚与板面内最小特征尺寸之比在1/80 ~1/5之间的板称为薄板[16]。 对于薄板,当全部外荷载作用于中面而不发生失稳现象,可以将其作为平面应力问题考虑;当全部外荷载都垂直于中面时,板主要产生弯曲变形。 由于薄板的厚度远小于薄板的平面尺寸,所以与梁弯曲的初等理论相似,完全可以略去某些非重要因素而引用一些能够简化理论的假设[17]:
(1) 变形前垂直于薄板中面的法线在薄板变形后仍保持垂直。
(2) 垂直于薄板中面方向的正应力σz在计算应变时忽略不计。
(3) 薄板发生弯曲变形时,中面内各点只有垂直于薄板z方向位移,即挠度w,而无x和y方向的位移u和v。
满足上述3 条基本假设,根据薄板小挠度弯曲理论,四边简支的矩形薄板边长分别设为a和b,受到荷载q(x,y)的作用,如图1 所示,其弹性力学边界条件的联立微分方程组为式(1)。 根据莱维重三角级数解,薄板挠度w表达式可以写成式(2),不难验证,式(2)满足了上述所有的边界条件。

图1 四边简支的矩形薄板Fig.1 Rectangular sheet simply supported on four sides

式中,m和n均为正整数;Amn为系数项。
式(2)除了满足边界条件外,还需满足薄板弯曲的基本方程,又称弹性曲面微分方程[式(3)],故将式(2)代入微分方程式(3)得到级数方程式(4),此时,系数Amn为求出具体挠度表达式的关键未知量。

式中,D为薄板的弯曲刚度;▽为拉普拉斯算子。

将式(4)等号左边的级数项看成q(x,y)的展开式,将其等号两边同乘,然后分别对x和y从0 到a和从0 到b积分,并利用式(5)、式(6)三角函数的正交性即可得到系数Amn的表达式(7)。


将式(7)代入式(2),即可得出挠度w的具体表达式,继而根据式(8)和式(9)可以求出薄板的横向弯矩Mx和纵向弯矩My。
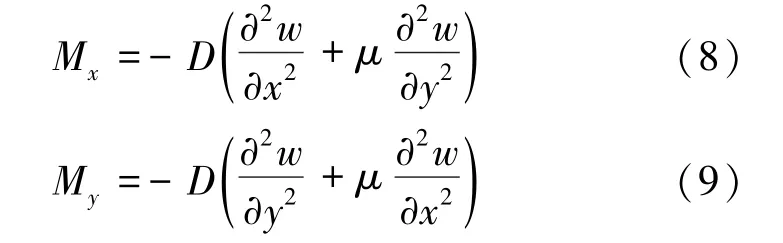
式中,μ为薄板的泊松比[17]。
2 一般公式的推导
为满足弯曲变形的要求,本文研究的基坑面层需满足以下的假设条件:
(1) 面层为均质线弹性材料。
(2) 面层满足薄板的基本特征,即面层厚度与面层的短边的比值在1/80 ~1/5 之间。
(3) 面层与基坑边坡土体为四边简支的联结方式。
(4) 面层垂直于基坑底面,且只考虑垂直于面层的侧向土压力作用。
基坑由于每次开挖均会造成开挖面的变化,而土压力的大小和分布范围也随开挖面变化,在此仅讨论基坑开挖喷射混凝土施工完毕后面层的受力状态。为给出计算面层挠度和弯矩的一般公式,同样设面层长为a,宽(沿基坑深度方向)为b,计算所采用的坐标系与图1 一致。 根据库伦土压力理论,沿基坑水平向同深度处的土压力均相等,此时面层所受的荷载q(x,y)可以看成只与y有关的线性函数。 在土的黏聚力c可忽略的情况下,荷载可以写成式(10)。

式中,γ为土的重度;φ为土的内摩擦角;y为土层深度。
将土压力荷载q(x,y)代入式(7)可得到系数Amn的一般显示表达式(11),再将得到的系数Amn代入挠度表达式(2),即可求得面层在土压力作用下的挠度一般公式(12)。 由于式中含有级数项求和,不方便工程计算使用,因此需进行合理的简化。


式中,m=1,3,5,…;n=1,3,5,…;D0为面层的弯曲刚度。
在实际工程中,面层的设计往往更关注其最大挠度值。 根据面层挠度计算式(12)不难看出,最大挠度发生在面层的中点,即x=a/2,y=b/2 处。 由于式(12)中级数项收敛很快,计算可知第二项值为第一项的1/729,第三项值为第一项的1/15 625,往后每项依次减小,故只保留第一项作为挠度的计算值。因此,面层在土压力下任意一点的挠度计算可以简化为
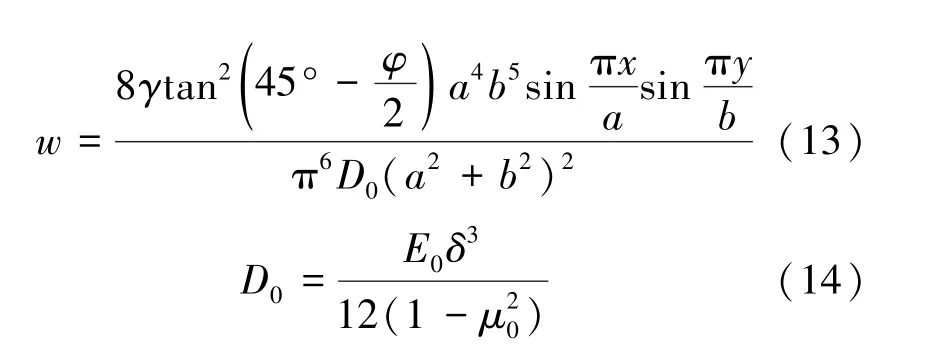
面层最大挠度的计算公式为
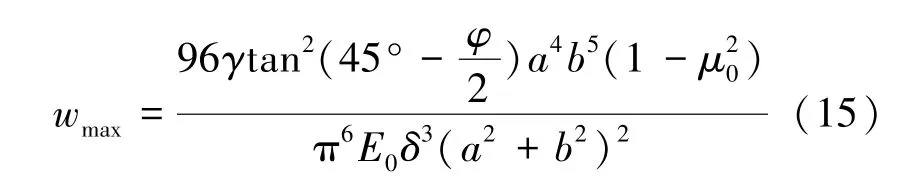
式中,E0为面层的弹性模量;δ为面层的厚度;μ0为面层材料的泊松比。
同理,将式(12)代入弯矩表达式(8)和式(9),同样级数项只取第一项,即得到面层任意点处x和y方向的弯矩计算式(16)和式(17)。

3 数值模拟
3.1 工程概况
某6 m×6 m×6 m 的小型基坑工程采用喷射混凝土支护形式。 基坑每开挖1.5 m 对基坑边坡土体进行一次喷射混凝土层施工,施工完成后基坑的支护面层与基坑底面几乎垂直。 采用的喷射混凝土强度等级为C30,支护面层厚度约为0.2 m。 基坑土层主要为砂土,土层及相关材料的物理力学参数见表1。

表1 材料物理、力学参数Table 1 Physical and mechanical parameters of the materials
3.2 数值分析
采用有限差分数值软件FLAC3D对该基坑工程进行模拟。 土层采用的是实体(Zone)单元,底边固定,约束前后左右面的法向位移,顶边为自由面。 由于实体单元在软件后处理中无法提取弯曲应力,故喷射混凝土面层选用壳(Shell)单元来代替。 用约束面层四周边缘的法向位移及四个角点处y、z方向的位移,来近似模拟面层四边简支的边界条件,计算准则采用Mohr-Coulomb。 模型计算前在面层上布置监测点,各点的坐标分别为面层中心点O(0,3 m,3 m)、1(0,3 m,4.5 m)、 2(0,4.5 m,3 m)、3(0,3 m,1.5 m)、4(0,1.5 m,3 m)、5(0,4.5 m,4.5 m)、6(0,4.5 m,1.5 m)、7(0,1.5 m,1.5 m)、8(0,1.5 m,4.5 m),如图2 所示。 计算后通过Fish 命令查看面层各个监测点的挠度值和弯矩值,将其与推导的理论公式计算值进行比较。

图2 监测点布置Fig.2 Layout of monitoring points
图3 为面层上各点的挠度云图。 根据任意点挠度计算式(13)的结构形式可知,挠度值的大小取决于分子的三角函数项。 因此,当两三角函数均取1 时,挠度值最大,当任意一个三角函数取0 时,挠度值即为0。 从几何角度看,凡过面层中心点O的水平线、竖直线及45°斜直线上关于点O对称坐标位置处的挠度值应相等,且中心点O处挠度值最大,围绕着中心点O向面层边界挠度逐渐减小到零。 这与数值模拟得到的面层挠度分布规律基本一致。
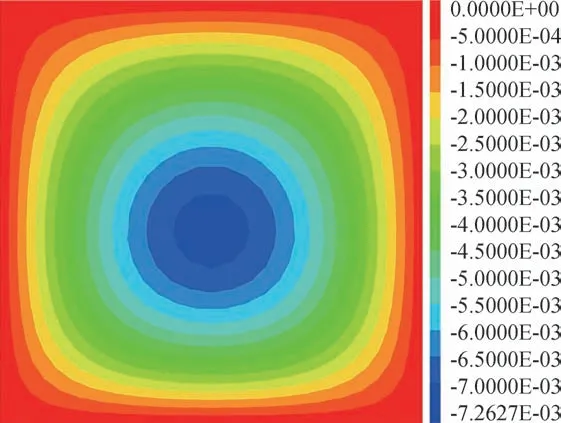
图3 面层挠度云图Fig.3 Deflection cloud diagram of surface layer
由于该基坑工程面层的长度a与宽度b相等,所以Mx、My表达式相同,计算出的弯矩值相等。 经数值模拟发现,面层弯矩Mx和My云图也基本相同(图4),进一步证明了理论计算公式的正确性。 从弯矩计算公式的形式上看,弯矩的分布主要取决于式中正弦函数乘积项的取值,而弯矩云图也基本符合公式的计算规律。 面层各监测点挠度和弯矩随时间步的监测曲线如图5、图6所示。 可以看出,挠度值和弯矩值均随着时间步先增大后减小,并最终稳定在某一数值保持平衡。 提取模型计算平衡后的挠度值和弯矩值,并将其与推导的公式计算值对比分析。 各监测点的挠度及弯矩的计算值和模拟值以及两者之间的相对误差见表2 和表3。 对比发现,挠度理论计算值与数值模拟值基本接近,最大差值为1.07 mm,其余监测点误差均在1 mm 以内,弯矩的理论计算值和数值模拟值误差均在20% 以内。 而在工程实际中,关注的是面层的最大挠度和最大弯矩值,通过理论计算和数值模拟结果对比发现,最大挠度和最大弯矩的误差分别为6% 和13% ,满足规范中误差不超过15% 的要求。
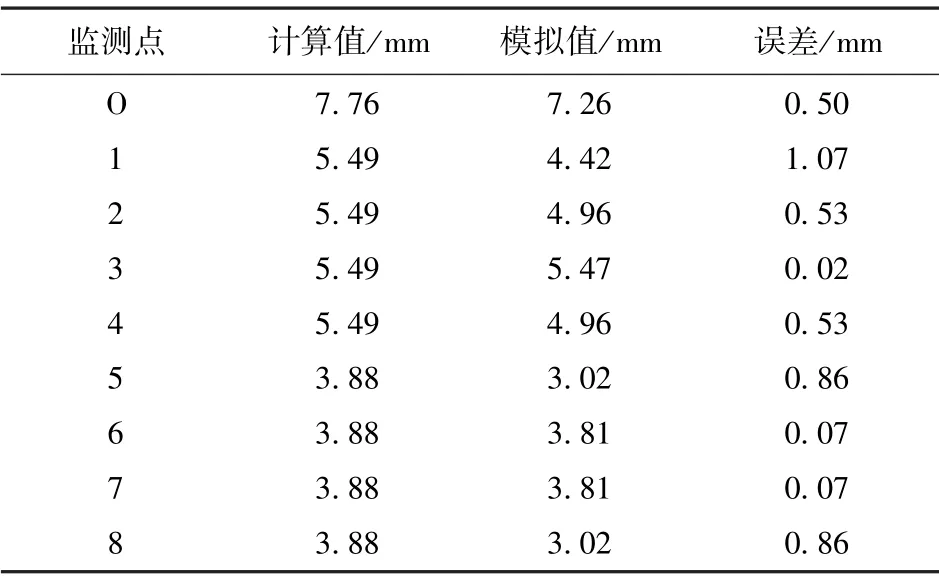
表2 面层各点挠度的计算值和模拟值Table 2 Calculation and simulation values of the surface layer deflection

表3 面层各点弯矩的计算值和模拟值Table 3 Calculation and simulation values of the surface layer bending moment

图4 面层弯矩云图Fig.4 Bending moment cloud diagram of surface layer

图5 挠度监测曲线Fig.5 Deflection monitoring curves
从数值模拟结果可以看出:
(1) 面层的挠度、弯矩均是从中点向边缘逐渐变小的,中点附近处挠度和弯矩最大,面层四周边缘处挠度和弯矩基本为零,这与推导的公式计算结果规律一致。
(2) 数值模拟值与理论计算值得到的挠度和弯矩基本相近。 挠度误差最大值为1.07 mm,最小只有0.02 mm,平均误差为0.5 mm,而最大挠度值两者之间相差0.5 mm,这完全满足工程上的精度要求;弯矩误差在0 ~20% 之间,最大弯矩值两者误差为13% ,平均误差为12% 。 误差可能与模型网格划分、运算过程中数值迭代产生的误差及计算公式忽略的级数项等因素有关。
4 结 论
(1) 利用薄板小挠度弯曲模型对喷射混凝土支护面层的内力和变形进行分析计算是可行的。
(2) 通过理论推导,得到了主动土压力下面层任意位置处挠度及x与y方向弯矩值的一般表达式,并用FLAC3D验证了公式的有效性,最大挠度和弯矩的计算值与模拟值之间误差分别为6% 、13% 。
(3) 推导的式(15) ~式(17)可用于类似基坑支护工程面层的内力和变形计算,为面层的设计提供参考。

