基于真实细观结构的FFT数值方法对岩石材料非线性力学行为的研究

李明耀彭磊左建平王智敏李绍金薛喜仁

中国矿业大学(北京)力学与建筑工程学院,北京 100083

岩石是自然界常见的非均质材料,其内部包含许多细观结构,如矿物夹杂、微裂隙和微孔洞等[1-2]。 这些细观结构特征改变了岩石的局部应力分布,进而影响其宏观力学行为和破坏过程[3]。因此,在研究岩石的宏观力学问题时,必须考虑其细观结构的影响。 由于岩石的细观结构具有很大的随机性,而且不容易观测,因此很难通过实验直接建立岩石细观结构与宏观力学性能的联系。 通过数值模拟分析岩石细观结构与其宏观力学性能的联系已经成为一种趋势[4-5]。

目前,数值方法被广泛应用于研究岩石宏观性能和细观结构之间的联系,常用的数值方法主要有基于连续体、不连续体的方法和混合方法等[6-7]。 有限元法(FEM)和有限差分法(FDM)都是基于连续体的数值方法,被广泛应用于模拟岩石的宏观力学行为。 于庆磊等[8]采用有限元法对花岗岩进行了单轴压缩数值模拟实验,研究了岩石细观结构对其变形和强度的影响。 朱泽奇等[9]采用有限差分法模拟了花岗岩的破坏过程,研究了岩石细观结构对其破坏过程的影响。 然而,有限元法和有限差分法在建立数值模型时需要生成大量的网格,岩石细观结构的几何形状是复杂多变的,这对网格生成技术造成了较大的困难。

基于不连续体的数值方法,颗粒流分析法(PFC)最为常见。 Hu 等[10]采用了基于颗粒的离散元模型模拟了北山花岗岩的损伤过程,研究了北山花岗岩的宏观力学和微裂纹行为。 韩振华等[11]采用基于颗粒流的离散元模型模拟了不同粒径花岗岩的破坏过程,研究了矿物粒径对其破坏形式和裂纹形态的影响。 PFC 方法的优势是可以有效还原岩石的细观结构,并且可以通过统计化学键的断裂数量来模拟岩石细观结构的破坏过程。 但是,PFC 方法没有考虑颗粒本身的变形和失效过程,而且在模型参数标定方面也存在一定的困难。

近年来,基于快速傅里叶变换(Fast Fourier Transforms,FFT)的数值方法作为一种无网格方法,被逐渐应用于岩石材料的数值模拟。 Li 等[12]采用基于FFT 的数值方法研究了脆性岩石的细观结构对其宏观力学行为和破坏过程的影响。Escoda 等[13]利用基于FFT 的数值方法研究了混凝土细观结构对其局部应力和宏观力学性能的影响。FFT 方法作为一种无网格的数值方法,可以更真实地还原岩石的细观结构,简化了各种复杂细观结构的几何形状的网格化过程。 同时,作为一种可以直接进行全场模拟的数值方法,有大量的开源数据库的支持,而且对于求解具有复杂细观结构的问题仍具有较高的计算效率[14]。

在过去的研究中,通常通过定义随机参数将岩石的非均质性纳入到数值模型中[15]。 例如,将岩石的细观结构简化为随机分布的颗粒形状来研究岩石非均质性的影响。 Li 等[16]利用计算机重建的方法复制岩石初始的细观结构,以此来考虑岩石的非均质性,并探究了黏土岩的非均质性对其破坏过程的影响。 这些方法虽然在一定程度上考虑了岩石非均质性的影响,但是随机参数的选取具有很大的主观性,并且局限于统计分布。 随着X 射线衍射(XRD)、扫描电子显微镜(SEM)和计算机断层扫描(CT)等实验技术的发展,为数字图像处理技术(DIP)在数值模拟中的应用提供了条件。 Yue 等[17]提出了利用DIP 技术将岩石细观结构纳入到有限元模型的方法,并研究了岩石材料的非均质性。 Wu等[18]提出了一种基于数字图像处理的FDEM 模型,研究花岗岩细观结构对其宏观力学行为和破坏过程的影响。 Tan 等[19]利用DIP 技术和Voronoi 镶嵌过程将花岗岩的细观结构细分成随机的子块,通过控制子块的尺寸和分布来考虑岩石的非均质性,以此研究了花岗岩的非均质性对其破坏过程的影响。

上述研究考虑了岩石非均质性的影响,并且提出了许多方法来研究岩石材料细观结构对其宏观力学性能的影响。 但是,有限元法(FEM)和有限差分法(FDM)等[8-9]在建立模型时需要生成大量复杂的网格,颗粒流分析法(PFC)[20]无法考虑颗粒本身的变形和失效过程,而且对模型参数的定义存在一定的局限性。 采用随机生成的方法[21-22]将岩石的细观结构等效为随机分布不同形状的颗粒,只能近似模拟,无法真实还原岩石的细观结构,而且这种考虑岩石非均质性的方法局限于统计分布的参数。

鉴于此,为了更准确地研究岩石材料的真实细观结构对其宏观非线性力学行为的影响,本文提出了一种可以直接与数字图像有机结合的FFT 数值方法,主要内容包括:

(1) 岩石细观结构的数字图像表征。 对岩石表面图像进行数字图像处理,获取其细观结构表征图像。

(2) 建立真实细观结构的数值模型。 利用FFT 数值方法可直接导入像素信息的优势,得到还原岩石真实细观结构的数值模型。

(3) 建立合理的细观本构模型。 根据岩石内部不同矿物所表现出的局部力学性能,建立合理的局部本构模型,如线弹性模型、弹塑性模型、损伤模型等。

(4) 力学计算及分析应用。 利用FFT 数值方法进行力学计算和全场数值模拟,得到岩石细观的应力场的演化过程,并与实验数据对比分析,得到细观结构与宏观力学行为的内在联系。

1 岩石细观结构的数字图像表征

数字图像处理技术(Digital Image Processing,DIP)是利用计算机将图像转化为数字矩阵,然后利用图像处理方法对数字矩阵进行分析和处理的过程[23]。 相比于用随机参数表征岩石非均质性的方法[15,24],DIP 技术能够更真实地模拟岩石细观结构,是将岩石细观结构纳入数值模型更合理的方法。 由于岩石类材料其内部不同的矿物成分在数字图像上表现为不同的颜色,因此DIP 技术在岩石表面图像处理方面存在特定的优势,在获取岩石内部信息中得到了广泛应用[17]。

1.1 岩样的矿物成分与分布

本文以法国ANDRA 地下研究实验室的Callovo-Oxfordian(COx)黏土岩为研究对象[25],详细阐述所提出的基于真实细观结构的FFT 数值方法在岩石力学领域的应用。 图1 为COx 黏土岩样品在扫描电镜下采集的灰度图像,分辨率为250 μm。 COx 黏土岩中的矿物因化学成分不同而具有明显不同的颜色和颗粒大小,主要由方解石(浅灰色大颗粒)、石英(深色大颗粒)和黏土(黑色散状颗粒)3 种矿物组成。 此外,还有少量其他矿物和孔洞(因其含量很少,可以忽略),本文根据力学性质将其归于性质较接近的区域。

图1 COx 黏土岩灰度图像Fig.1 Gray image of the COx claystone

图1 所示COx 黏土岩的灰度图像中,虽然各种矿物可以根据图像中的颜色大致区分为3 类,但同一矿物成分的灰度在特定区域仍然有深有浅,而且有些区域不同矿物之间的灰度值较为接近,因此很难严格确定不同矿物的区域和边界。 灰度图像是由大量像素组成的二维矩阵,每个像素具有确定的位置信息和亮度信息,灰度值的取值范围为[0,255],表示像素由黑色到白色的变化过程。 由图1 可以看出,COx 黏土岩灰度图像中,石英和黏土区的灰度值较为接近,而方解石区与其余区域差异明显。 因此,为了准确描述岩石内部细观结构,必须对灰度图像进行处理,从而严格区分出3 种不同矿物的区域和边界。

1.2 岩石细观结构的数字图像表征过程

基于上述黏土岩灰度图像特点的分析,为了更好地区分黏土岩内部的方解石、石英和黏土矿物,对其细观结构的数字图像需分2 个步骤进行处理:

(1) 从整体图像中表征方解石矿物;

(2) 在其余区域表征石英矿物和黏土矿物。

表征过程如图2 所示。

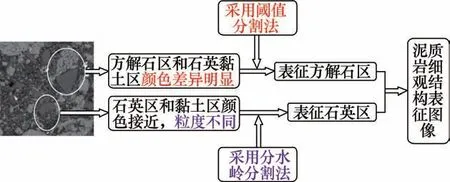
图2 基于COx 黏土岩细观结构表征的流程Fig.2 Flow chart based on microstructural characterization of COx clay rock

1.2.1 方解石矿物区域的表征

如图1 所示,在灰度图像中,方解石区呈浅灰色,而石英和黏土区均呈深黑色。 方解石区与其他区域呈现出明显不同的颜色,其灰度值差异较大,因此将方解石矿物从整体区域中区分出来是相对比较容易的。 本文采用阈值分割法对其进行分割处理,将同一阈值分段里的像素归为同一种矿物,用公式(1)描述[26]:

式中,G(x)为表征图像中像素点的值;f(x,y)为原始灰度图像像素的灰度值;ζn为所选用的阈值。

常用的阈值分割法主要有灰度直方图分割法和基于扫描线确定阈值的分割法,灰度直方图分割法比较适用于图像灰度直方图出现多个峰值,阈值在相邻峰值之间的峰谷选择[26]。 由于COx 黏土岩图像的灰度直方图峰值单一、没有明显的峰谷,所以本文采用基于扫描线上确定阈值的分割方法。 如图3(a)所示,在COx 黏土岩的原始图像上选择一条白色扫描线,必须穿过方解石区和石英与黏土区,并且两个区域矿物的颗粒肉眼可以区分。 白色扫描线上灰度值的变化曲线如图3(b)所示。 通过比较图3(a)中扫描线穿过的区域变化与图3(b)中曲线的变化情况可以发现,石英和黏土区的灰度值在红色线以下,而方解石区的灰度值在红色线以上波动。 经过多次实验,最终确定灰度值99 为方解石区与石英黏土区的阈值。 因此,在灰度图像矩阵中,凡是灰度值大于阈值99 的像素都归为方解石区。 由此,可以得到方解石的表征图像,如图3(c)所示的红色区域。 通过对比灰度图和表征图,方解石区的表征图像能很好地反映其真实细观结构。

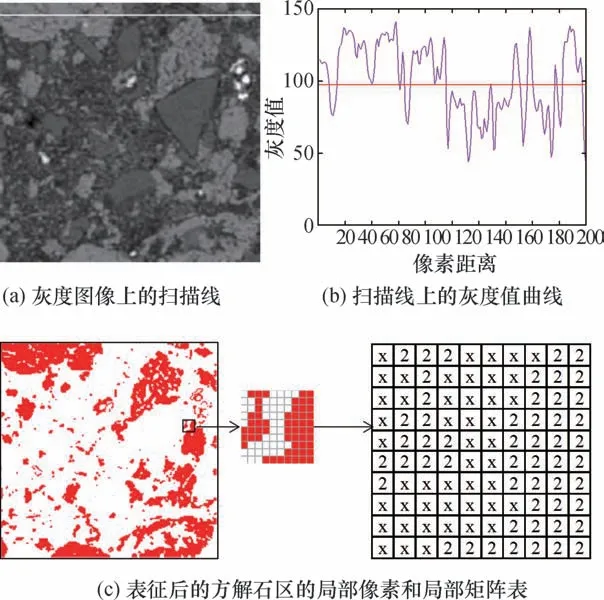
图3 方解石矿物的表征过程Fig.3 Feldspar mineral characterization process

由此可见,DIP 技术提供了一种更合理的方法来模拟岩石内部复杂的初始细观结构。 经过DIP技术处理后获取的细观结构表征图像,本质上是由像素组成的二维矩阵。 每个像素都有确定的位置信息和颜色信息,用数字可以表示为(i,j,I)(其中i和j代表像素的位置,I代表像素的颜色属性)。以COx 黏土岩为例,由于其细观结构表征图像有3 种颜色属性,本文采用数字来替换像素的颜色属性,1 代表黏土,2 代表方解石,3 代表石英。 因此,黏土区、方解石区、石英区像素的数字形式分别为(i,j,1)、(i,j,2)、(i,j,3)。 这样,就把200×200 像素的COx 黏土岩细观结构表征图像转化为由数字1、2、3 构成的200×200 的二维数字矩阵。

对方解石矿物表征后的图像如图3(c)所示,将局部区域放大可以看出其对应的矩阵表,数字2代表方解石矿物区,字母x 代表还未区分的黏土(数字1)和石英(数字3)。

1.2.2 石英矿物区域的表征

如图1 所示,石英区和黏土区的灰度值较为接近,但是石英和方解石颗粒的尺寸大于黏土颗粒,它们形成了均匀的区域,该区域的局部灰度变化不大。 所以,本文采用在局部方差图像上用分水岭分割算法对石英区和黏土区进行分割[25]。

分水岭分割算法把灰度图像看成一幅地形浮雕,亮度强的区域灰度值较大,亮度暗的区域灰度值较小,通过寻找汇水盆地和分水岭界线对图像进行分割。 分水岭分割方法有时会产生过度分割的现象,为了减少这种情况,需要在分割前对图像进行高斯滤波处理。 首先,计算COx 黏土岩原始图像的局部方差(在石英黏土区进行,排除方解石区灰度值的影响),获取原始图像的局部方差图像[图4(a)]。 从图4(a)中可以区分出与石英相关的均匀区域,从而可以将黏土与石英分割开。 其次,在滤波后的局部方差图像上[图4(b)]进行分水岭分割算法,得到局部方差的分水岭分割结果图[图4(c)]。 由于局部方差图像上显示的石英区只是真实的一部分[图4(d)],因此,将局部方差图像上显示的石英区的边界与分水岭分割算法结果图相结合,重新识别石英区。 最后,保留分水岭分割算法结果图中与局部方差图像中石英区相对应的盆地,将其识别为石英区[图4(e)]。 通过与原灰度图像对比可以看出,经过分水岭算法分割图像的石英区能准确地表征其边界。

图4 石英矿物的表征过程Fig.4 Process of quartz mineral characterization

1.2.3 黏土矿物区域的表征

经过上述两步,将阈值分割法确定的方解石区[图3(c)]和分水岭算法确定的石英区[图4(e)]相叠加之后,剩余区域就是黏土矿物区。 最终,就可以得到COx 黏土岩整体细观结构的表征图像,如图5 所示。 与原灰度图像(图1)对比可见,通过DIP 技术得到的岩石细观结构表征图像能较准确地描述岩石的细观结构特征。

图5 COx 黏土岩的细观结构表征Fig.5 Microscopic characterization of COx argillaceous rocks

2 数值方法

2.1 基于快速傅里叶变换的数值方法

基于快速傅里叶变换(FFT)的数值方法是文献[27-28]提出的,用于计算复杂细观结构的非均质材料力学行为的数值计算方法。 基于FFT 的数值计算方法可以直接利用图像中的像素点作为材料点,与传统的数值模拟方法相比无须再考虑复杂细观结构的边界。 依据像素所属的材料,赋予对应材料点相应的力学属性,以此来将复杂的细观结构特征引入到FFT 模型中。 与FFT 方法相比,传统的数值方法在表征岩石复杂的细观结构时,需要生成大量的网格;越复杂的细观结构,网格的划分越困难;大量的网格又影响了数值模拟的计算效率。 近年来,越来越多的学者将基于FFT 数值计算方法应用到数值模拟领域中,FFT 方法得到了发展和进步,并被用来研究孔洞和夹杂的问题[29-30]。

以非均质线弹性材料为例,现介绍基于FFT的数值计算方法。 材料单元在边界∂V上受到一个均匀的宏观应变任意一点的局部应变ε(x)可由Lippmann-Schwinger 方程求得

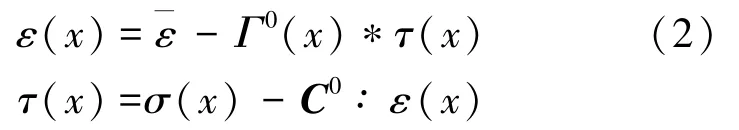
式中,*为卷积符号;τ(x)为线弹性和均匀介质中“非均质部分”的极化应力;σ(x)为局部应力;C0为均匀介质的弹性张量,与材料的局部位置x无关。

格林算子Γ0在傅里叶空间中可以表示为

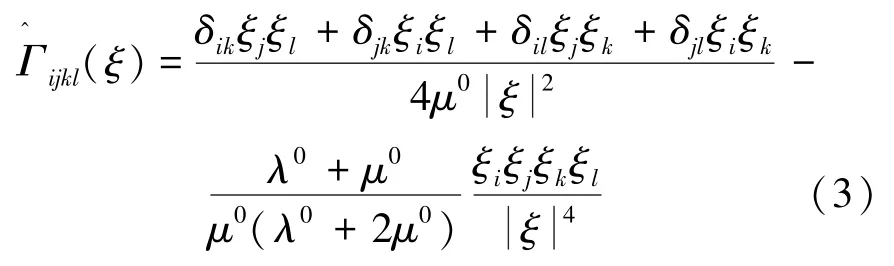
式中,ξ为傅里叶空间中的离散频率;λ0和μ0为材料介质的拉梅系数;δ为Kronecker's delta。

由公式(2)求得代表单元内任意一点的局部应变ε(x)后,即可通过代表单元体内的弹性张量C(x)求得对应的局部应力σ(x)。C(x)严格依赖于局部坐标位置x。 材料的宏观应力可由整个单元局部应力的体积平均值计算:

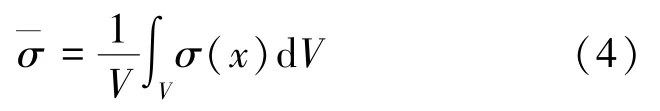
针对非线性问题,本构关系可以采用增量形式表示,即将总的加载过程划分为有限的N步,从初始条件到n步的局部应力σn,局部应变以及内部变量Vn都是已知的。 对于宏观应变增量在n+1 步时,局部非线性本构关系可以用式(5)增量形式表示:

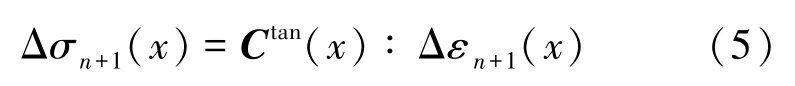
式中,εp(x)为非线性局部应变增量,如塑性应变;Ctan为与加载历史和加载方向有关的切线4 阶张量。

2.2 基于真实细观结构的FFT 数值方法的建立

FFT 方法的主要优势在于避免了对非规则复杂细观几何形状的网格划分,取而代之的是一系列离散的材料点来模拟非均质材料的细观结构特征。通过材料点的位置信息和材料属性的对应关系即可准确获得非均质材料的细观结构特征和与其对应的力学性质。 因此,可以直接将经过图像处理的岩石真实细观结构表征的图像像素信息(数字矩阵)作为FFT 方法的材料点,导入到FFT 程序,并根据数字所属矿物的种类赋予相应的细观力学参数,就可以进行计算分析。

如图6 所示,首先获取岩石的数字图像[图6(a)],然后提取图像的像素信息得到每一个像素的位置信息和颜色信息[如图6(b)],最后进行图像分割得到细观结构表征图像[图6(c)]。 图6(c)中的像素值就是FFT 方法中的材料点,可以直接将其导入FFT 算法建立几何模型,然后根据像素信息确定每个像素点的力学性质。 因此,用于计算分析的FFT 模型与COx 黏土岩的细观结构表征图像完全一致,真实完整地反映了岩石内部的细观结构。 综上所述,基于真实细观结构的FFT 数值计算方法的流程如图7 所示。

图6 材料点生成过程[18]Fig.6 Material point generation process

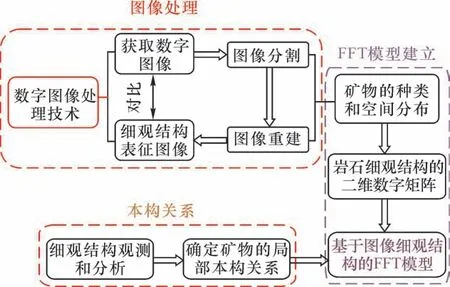
图7 基于真实细观结构的FFT 数值计算方法流程Fig.7 Flow chart of the actual-mesostructure-based FFT numerical method

基于真实细观结构的FFT 模型直接利用了像素原有的信息,不需要进行任何处理,考虑了岩石的非均质性。 同时,对于同一形状的物体,像素越高,细观结构的边界越接近真实的边界(图8)。 因此,基于真实细观结构的FFT 数值方法在模拟岩石细观结构上具有理想的效率和准确性。

图8 像素对边界的影响[31]Fig.8 The effect of the pixel on the boundary

2.3 细观本构模型

在分析COx 黏土岩矿物成分和细观结构的基础上,依据黏土基质、方解石和石英矿物的力学性能,选择合理的局部本构模型。 研究发现,黏土矿物的拉伸和抗压强度相对较低,在荷载作用下容易产生较大的变形。 因此,黏土矿物可以选用弹塑性本构模型。 与黏土矿物相比,方解石和石英的矿物颗粒尺寸远大于黏土,相对坚硬,不易变形,可以采用线弹性模型[18]。 为了更准确地描述本研究所使用的局部本构模型,图9 给出各种矿物的局部本构曲线示意图。

图9 细观结构和局部本构模型的关系[12]Fig.9 Relationship between microstructure and local constitutive model

石英和方解石采用线弹性模型,只需要确定弹性模量和泊松比即可。 而根据黏土矿物的力学性质,本文采用非关联Drucker-Prager 准则来描述其非线性力学行为

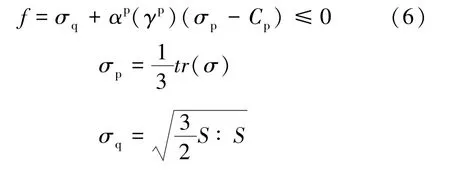
式中,σp为平均应力;σq为等效应力;S为偏应力张量;Cp为材料内聚系数;αp(γp)为摩擦系数;γp为等效塑性剪切应变,为αp的内变量。

本文采用了各向同性塑性硬化规律,用公式表示为

式中,为摩擦系数的初始值;为摩擦系数的最终值;b为控制硬化速率的系数。

为了更好地描述COx 黏土岩的塑性体积应变,采用非关联流动准则,塑性势能函数表示为

式中,βp为塑性体积膨胀系数为塑性体积膨胀系数的初始值;为塑性体积膨胀系数的最终值;b1为控制塑性体积膨胀速率的系数。

针对非线性问题,局部本构关系以增量的形式可表示为

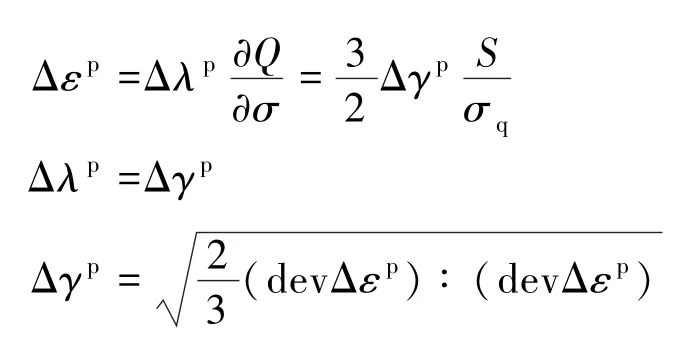
式中,Cm为基质的弹性刚度张量;Δεp为塑性应变增量;Δλp为塑性乘子;dev 为偏量。

Δεp和Δλp的值受当前塑性状态和加载/卸载准则的影响,最终由塑性一致性条件确定。

3 数值验证与分析

3.1 参数标定与宏观力学行为的预测

将本文提出的基于真实细观结构的FFT 数值方法用于模拟COx 黏土岩的力学行为。 首先对模型参数进行标定。 方解石和石英弹性参数采用文献[32]中测得的实验值。 参照COx 黏土岩、方解石和石英的宏观弹性参数的实验值,采用Mori-Tanaka 方法反向求取了黏土基质的弹性参数[16]。 FFT 模型弹性参数标定的结果见表1。 文献[32]对不同深度的COx 黏土岩进行成分测量,不同深度所含矿物的含量是不同的。 为了提高数值模拟的准确性,运用数字图像处理技术对每个深度岩石的表面图像进行了表征,将岩石的细观结构纳入数值模型中。 统计了不同矿物所对应的像素信息,最终得到FFT 模型中矿物含量与实验测得含量的对比结果(表2)。

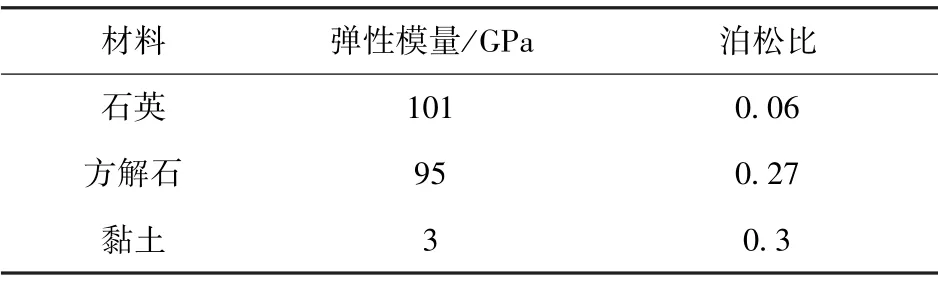
表1 COx 黏土岩细观介质的弹性参数[32]Table 1 Elastic parameters of meso-medium of COx clay rock

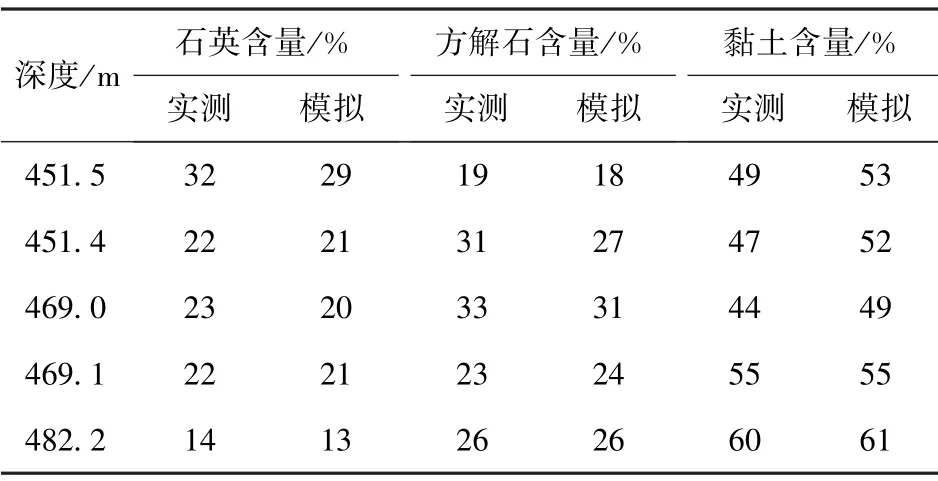
表2 不同深度各种矿物的含量[32]Table 2 The content of various minerals at different depths

利用深度为482.2 m 的COx 黏土岩样品,在围压为10 MPa 下的三轴压缩实验来标定黏土基质的塑性参数,如图10 所示。 将数值模拟曲线与实验曲线拟合,取最优的一组参数,最终的非弹性参数结果如下-3.9,0.1,b=170,b1=300。

图10 参数标定Fig.10 Parameter calibration

文献[32]对不同深度下的COx 黏土岩进行了三轴压缩实验,本文对深度为451.4 m、469.0 m、469.1 m、482.2 m 和451.5 m 的样品进行了数值模拟实验,并且预测了不同深度、不同围压下的宏观力学行为。 首先,依照数字图像处理的结果,将COx 黏土岩的细观结构纳入数值模型中,并按照对应的本构关系和标定的参数进行计算,最终的对比结果如图11 所示。

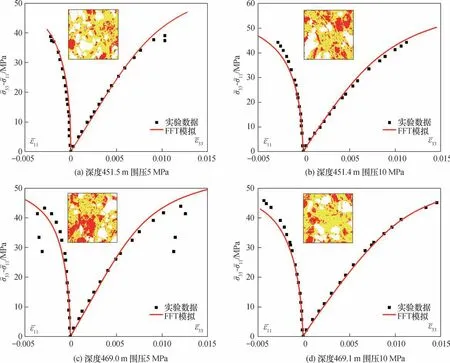
图11 数值模拟与三轴压缩实验数据的对比Fig.11 Comparison of numerical simulation and experimental data

从数值模拟和实验数据对比结果可以看出,本文提出的基于真实细观结构的FFT 数值计算方法能根据岩石不同细观结构预测其宏观力学行为,不同深度、不同围压下COx 黏土岩的塑性阶段轴线和侧向曲线均拟合较好,峰值强度的预测准确。FFT 模型真实地还原了岩石内部的细观结构,并且考虑了不同矿物的分布和相互作用。 但是模拟实验中没有考虑岩石的损伤阶段,没有考虑微裂纹、孔洞等缺陷对岩石宏观力学行为的影响,这些问题将会在今后的研究工作中进一步解决。

3.2 细观结构特征与局部应力分布

为了进一步揭示岩石细观结构特征与局部应力的影响,取上述4 组数值模拟的细观结构图及对应的应力云图(图12)。

由图12 可以看出,不同种类矿物的分布和形状直接影响局部应力场的分布。 应力较大的区域(浅绿色),主要集中在不同矿物的边界和细小的方解石区。 这是因为部分方解石矿物夹杂的形状较为细小且不均匀,受其非均质性的影响,这些区域容易产生局部应力集中现象,使得该区域的应力较大。 同时,在不同矿物的边界也容易产生应力集中现象。 石英区的应力除了一些边界会出现应力集中现象,其他区域的应力分布相对均匀(浅黄色),这是因为石英矿物夹杂是成块存在的,并且这些块状区域内不包含其他矿物,相对均质。 黏土矿物的区域最大,应力最小(深黄色区域),除去黏土内部包含的其他矿物,黏土的应力相对均匀分布于应力云图中。

图12 细观结构特征与局部应力Fig.12 Microstructure and local stress

综上分析,非均质岩石类材料的细观结构的分布和几何形状对其局部的应力分布有重要的影响。 本研究提供的细观结构局部应力的演化过程,可以合理地解释细观结构特征对其应力分布的影响规律。

3.3 细观结构与宏观力学行为的关系

为了进一步探索COx 黏土岩细观结构对其宏观力学行为的影响,本文以深度482.2 m 的岩石样品为例,利用基于真实细观结构的FFT 模型,给出了该样品在10 MPa 三轴压缩模拟试验的应力-应变曲线与细观应力云图之间的关系,如图13 所示。

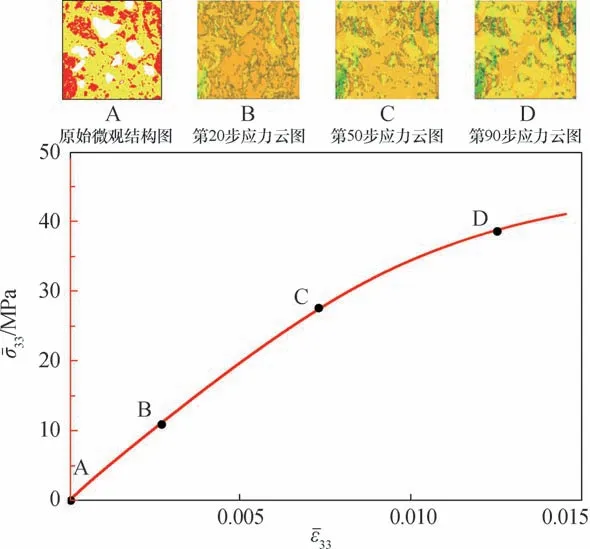
图13 细观结构应力演化对宏观力学行为的影响Fig.13 Influence of microstructure stress evolution on the macroscopic mechanical behavior

从B 点应力云图可以看出,黏土基质对应的应力值最小,方解石对应的应力值最大,石英的居中。 较大的应力值主要分布在方解石和黏土基质的分界线上,这是由于方解石分布不均匀,有较多的细小区域导致局部应力集中现象。 石英区相对均匀,应力分布相对均匀。 A-C 阶段云图变化比较迅速,大面积的黏土基质区由深黄色变为浅黄色(浅黄色代表应力较大的区域),每种矿物上升的幅度都很大,对应的整体宏观应力-应变曲线上升较迅速,应力变化范围较大。 当应力增加到图中的C 点时,黏土基质的应力继续增大,但是因为黏土基质采用的是弹塑性本构模型,此时大部分黏土矿物开始进入塑性阶段,应力变化范围较小,石英和方解石区的应力继续上升。 当曲线到达D 点时,黏土基质大部分区域的应力已经进入屈服,只有少数区域的应力还在增加,曲线应力的上升主要由石英和方解石控制。 石英和方解石区域的应力继续增加,石英区域增加较均匀,方解石受分布不均匀的影响出现了一些应力较大的区域,此阶段宏观曲线上升趋势进一步减缓。

可见,本文提出的数值方法可以从细观应力云图来可视化宏观力学行为的变化过程,合理解释细观结构特征与宏观力学行为之间的内在联系。

4 结 论

利用FFT 数值方法可以直接获取图像像素信息的特点,与数值图像处理技术有机结合,本文提出了一种考虑岩石内部真实细观结构特征的FFT数值分析方法。 在此基础上,以COx 黏土岩为例,研究了岩石内部真实细观结构对其宏观非线性力学行为的影响。 主要结论如下:

(1) 针对岩石具有复杂细观结构特征的特点,提出了基于真实细观结构的FFT 数值方法。 该方法无须划分网格,在研究岩石类材料时具有一定的优势。

(2) 实现了非均质性材料的力学分析,合理预测了不同赋存深度、不同围压下黏土岩的峰前非线性行为和峰值强度,以及细观结构特征对其宏观非线性力学行为的影响。

(3) 从细观尺度上揭示了矿物的含量、形状、大小和分布等特征对宏观力学行为的影响机理。 数值计算结果表明,岩石材料内部细观结构决定了材料的应力分布,显著影响材料的宏观非线性行为。