煤-气交叉开采区天然气井防碰撞预警技术研究

王文杨昆何云王斌高斐潘叶信

1.河南理工大学能源科学与工程学院,河南焦作 454003;2.煤炭安全生产与清洁高效利用省部共建协同创新中心,河南焦作 454000;3.中国石油化工股份集团有限公司华北油气分公司,河南郑州 450006;4.长江大学石油工程学院,湖北武汉 430100;5.惟其信石油机械(天津)有限公司,天津 300308

我国鄂尔多斯盆地、塔里木盆地以及准噶尔盆地等地区蕴含着丰富的煤炭、石油和天然气等矿产资源。 这些矿产资源形成了独具特色的平面上相互叠加、垂向上相互叠置的异体共伴生格局[1-3]。随着我国天然气、煤炭的开发力度进一步加大,单一矿种开发模式不能满足矿产资源有效利用的要求,且存在较为严重的浪费和环境污染[4-5]。 煤-气交叉开采逐渐常态化,暴露出来的安全问题也越来越多[6]。

以鄂尔多斯盆地为例,盆地内油气层埋深大于1 500 m,煤层埋深700 ～1 500 m,形成了天然气井穿越煤层的现象[7]。 盆地内煤与天然气主要赋存层位如图1 所示。 盆地内煤矿又多以千万吨级矿井为主,设计产量高,开采机械化程度高,巷道掘进施工和工作面回采速度快,巷道布置可能会处于天然气井附近,很可能会发生掘进机碰撞天然气井的情况,导致天然气大量泄漏至采掘空间,有爆炸、中毒和窒息的风险。

图1 鄂尔多斯盆地地质赋存层位Fig.1 Geological focal points of the Ordos Basin

目前,国内外在处理穿越开采煤层的天然气井时,主要有两种方法[8]:一是采掘活动进行到天然气井附近时对其进行封堵,以免天然气井失稳后,天然气进入工作面和地下含水层,引发矿井火灾、瓦斯爆炸、地下水污染;二是调整工作面开拓布局,使天然气井穿过煤柱。 众多学者在天然气井井壁稳定研究方面也取得了很多进展。 陈秀荣[9]根据地质力学理论、多孔弹性介质力学理论、岩石力学及声学理论,对井壁围岩的受力状态、地应力的测量技术、岩石强度的测定方法以及泥页岩水化应力及其分布的确定、相应计算方法等进行了系统的研究和分析。 金衍等[10]、刘向君等[11]分析了结构面发育对井壁稳定的影响,表明结构面的存在弱化了井壁的稳定性,井壁失稳与结构面的产状密切相关。 李忠华等[12]基于损伤理论分析井壁稳定问题。 李军等[13-14]使用有限差分及有限元等方法进行了井壁稳定性数值模拟分析,并基于多层组合厚壁圆筒理论,建立了套管、水泥环及井壁围岩组合体的力学模型,对均匀地应力作用下的组合体进行了弹塑性分析。 丁振龙等[15]建立三维井筒稳定模型,计算得到了井壁处的最大应力,为解决天然气井井壁稳定问题提供了理论依据。 余夫等[16]通过建立地层-水泥环-套管的力学模型,应用弹性力学理论引入压力传递系数概念,分析了水泥环和地层的弹性模量、泊松比对套管与水泥环力学状态的影响规律。 申昭熙等[17]认为套管抗挤强度主要由径厚比决定,屈服外压和失稳外压等参数及其交互作用对套管的抗挤强度也有显著影响,套管外径和壁厚数据的变异系数对套管抗挤强度的影响更显著。

上述文献中,众多学者针对煤-气交叉开采区内的天然气井保护,无论是留设保护煤柱,还是从天然气井本身的稳定性进行研究,均属于被动保护。 本文以鄂尔多斯盆地的煤-气交叉开采为研究对象,从主动保护方面考虑,通过研究采掘振动在煤层和天然气井中的传播衰减规律,实现主动监测采掘活动与天然气井的距离,从而预防碰撞事故的发生,以期解决煤-气交叉开采冲突问题,为类似地质条件的煤-气交叉开采提供参考。

1 天然气井防碰撞振动监测原理

巷道掘进过程中掘进机产生的巨大振动以振动波的形式向四周传递。 当振动波传递至天然气井时,天然气井将发生受迫振动,振动波会沿着天然气井井筒继续向上传递直至地表井口。 假设掘进机在掘进过程中产生的振动强度不变,基于振动波在煤岩层中传播的衰减规律,振动振幅能量随传播距离的增加呈指数关系衰减。 如果掘进施工距离天然气井较远,则掘进产生的振动传播到天然气井时衰减较大,振动传递至地表井口的振动信号也较弱,表现在地面监测到的振动信号幅值、能量较小;当掘进工作面接近天然气井时,振动传播到天然气井时衰减变小,此时传递到井口的振动信号变强,表现在地面监测到的振动信号幅值、能量变大。因此,振动信号的幅值、能量与掘进工作面距风险天然气井间的距离存在对应关系:掘进工作面距天然气井距离增大时,振动信号的功率谱相对幅值逐渐减小;反之,则逐渐增大。 利用安装在天然气井套管头的振动传感器拾取掘进机破碎煤岩传播出来的振动信号,通过分析掘进机破碎煤岩时产生的振动波沿地层和套管的传播规律,建立天然气井地面套管头采集到的振动信号特征与巷道掘进工作面到天然气井距离的关系,根据信号识别实现对巷道掘进趋近天然气井的监测,原理如图2 所示。

图2 防碰撞监测原理示意图Fig.2 Diagram of anti-collision monitoring principle

2 振动监测试验方法

2.1 监测试验及信号采集装备

试验均采用IEPE 压电式加速度传感器,传感器型号为1A213E,轴向灵敏度100 mV/(m·s-2),量程49 m/s2,频响范围0.2 ～4 000 Hz。 该传感器具有高灵敏度、高分辨率,基座应变小、与地绝缘和抗干扰好以及低阻抗电压输出等特点,主要用于地震试验和建筑振动、地面振动、地基振动、坝体振动等监测。

采集仪采用动态信号测试分析系统(DH5981),能够实现实时高效的数据传输,所有通道同步采样,每通道采样频率最高128 kHz;同时具有智能化锂电池组管理,可持续工作6 h。 该采集仪与笔记本电脑相连接,通过专用数据处理软件实现采集、记录、传输和保存功能。

2.2 钢管敲击振动试验方案

以N80 级φ177.8 mm×9.19 mm 钢管为介质进行敲击振动传播衰减试验,材质与天然气井相同,增加振动试验的可靠性,钢管水平放置,在钢管上侧距振源0 m、10 m、20 m、30 m、40 m 处布置IEPE 压电式加速度振动传感器,传感器通过IEPE信号输入线连接至DH5981 信号采集仪,并输出到电脑端,如图3 所示。 设备连接完成后进行试验,通过力锤水平敲击1 号振动传感器所在端的钢管,查看电脑端是否能够正常接收到各测点的振动信号。 设备连接无误并确保周围环境安静、无噪声的干扰后,方可进行试验。 试验采用力锤对钢管进行敲击,敲击力度保持不变,进行多次敲击试验避免偶然误差,采集仪实时接收各测点振动波加速度等参数的信号(以下简称试验1)。

图3 钢管敲击振动试验示意图Fig.3 Diagram of the steel pipe percussion vibration test

2.3 井下现场掘进振动试验

井下掘进振动试验是掘进机进行掘进时,分别在距掘进机不同距离处布置振动传感器进行监测,研究掘进机破碎煤岩时产生的振动波在煤岩中传播衰减特性,从而发现振动波在煤岩介质中的传播衰减规律。 掘进振动试验采用均方根值进行分析。均方根值更能够表现振动波从开始振动到振动结束整个过程中振动波的整体振动强弱。

2.3.1 试验地点

鄂尔多斯盆地北部地区多数煤矿开采煤层结构简单,一般不含夹矸或局部含1 ～2 层夹矸,振动波传播过程中受实体煤外介质影响较小,试验地点对煤层完整性有一定要求。 16061 工作面回风巷已经成型,没有人员施工的影响,避免了施工产生的干扰振动信号,能够得到较为准确的掘进振动信号。 因此,试验地点选在16061 工作面。 该工作面位于矿井北翼,开采煤层为21煤层。 该工作面回采长度1 550.99 m,宽150 m。 16061 回风联络巷与该回风巷夹角为70°,该联络巷还有20 m 即将贯通,为试验提供了条件。

2.3.2 试验方案

如图4 所示,布置1 ～4 号振动传感器。 1 号振动传感器布置在16061 回风联络巷掘进贯通点。沿回风巷道在20 m、50 m、80 m 处依次布置2 ～4号振动传感器,振动传感器布置在联络巷贯通处一侧的巷帮锚杆上。 计算得到传感器距振源距离(表1)。 为保证数据普遍性和丰富性,现场进行多次试验(以下简称试验2)。

表1 煤矿试验传感器布置及距振源距离Table 1 Coal mine test sensor arrangement and distance from vibration source

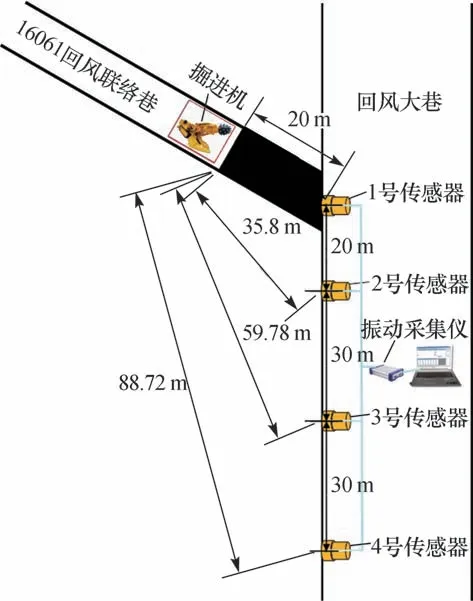
图4 井下掘进振动试验传感器布置示意图Fig.4 Diagram of underground excavation vibration test sensor arrangement

3 试验结果及讨论

3.1 钢管振动衰减规律分析

选取试验1 中有代表性的4 组数据进行分析。 图5 为钢管振动试验1 的各测点振动时域图。 可以看出,随着远离振源,振动波振幅及其均方根值都发生了明显衰减,衰减速度先快后慢。 振动波的均方根值又称为有效值,是振动波平均能量的一种表达,故以均方根值为参数进行具体分析。 为方便分析,减少试验过程中因敲击力度不同的影响,分别提取试验1 中4 组试验各测点的均方根值并进行归一化处理(表2)。 对归一化后的振动信号均方根值进行指数拟合,结果如图6 所示。 从拟合结果来看,R2均超过0.96,指数函数拟合效果较好,并符合振动衰减通式A=A0e-αr。 通过指数拟合曲线可以看出,振动波在衰减过程中衰减速度先快后慢,平均衰减系数为0.1。 这说明以天然气井为介质进行振动传播衰减规律研究,实现防碰撞监测预警技术中天然气井段振动监测是可行的。

图5 钢管振动试验1 各测点时域波形Fig.5 Time domain waveforms at each measurement point of steel pipe vibration test 1

图6 钢管振动1 ～4 组均方根归一化指数拟合曲线Fig.6 Fitted graphs of the root mean square normalised index for steel pipe vibration groups 1 ～4

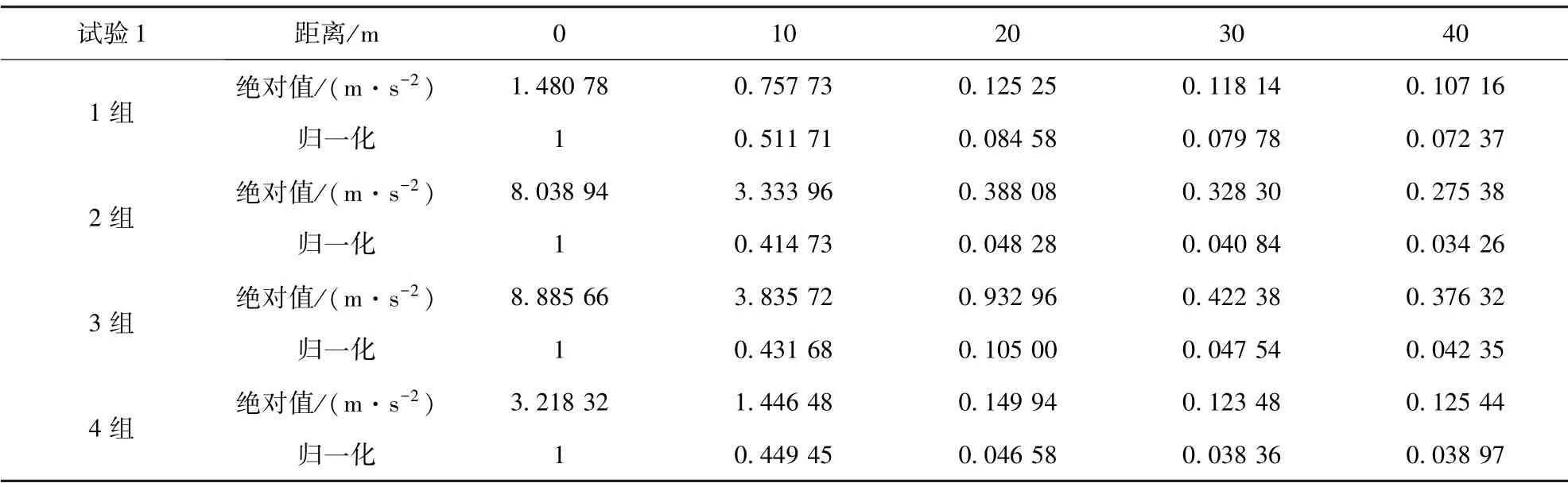
表2 钢管振动波有效值及归一化Table 2 RMS values and normalisation of steel pipe vibration waves

3.2 井下现场掘进振动衰减规律分析

选取试验2 中具有代表性的4 组井下振动试验数据进行分析,通过分析均方根值的衰减情况研究振动波的衰减。 图7 为现场振动试验振动波时域图,可以看出,振动幅值及均方根值均发生明显的衰减。 对表3 中归一化后的均方根值进行指数函数拟合处理,结果如图8 所示。 可以看出,拟合优度R2平均值为0.98,拟合效果很好,指数拟合公式符合振动衰减通式A=A0e-αr,振动衰减先急速下降后缓慢降低,平均衰减系数为0.03。 同时说明,以煤岩为介质进行振动衰减规律研究,实现防碰撞监测预警技术中煤岩段振动监测是可行的。

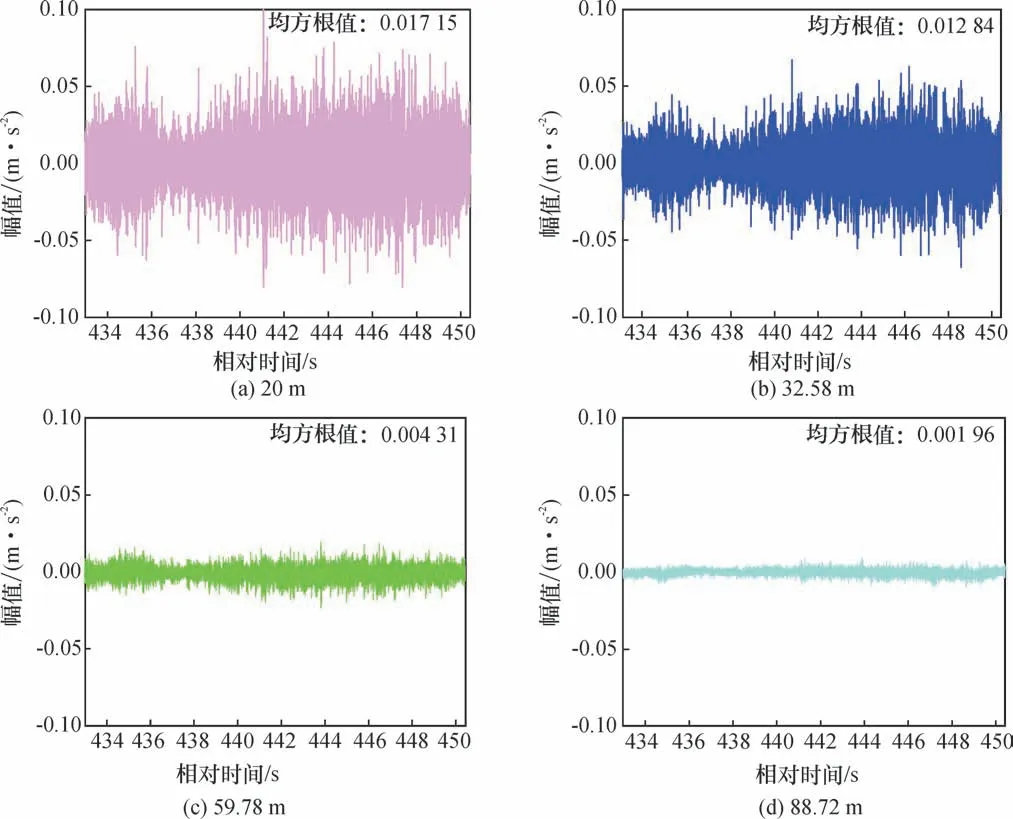
图7 井下掘进振动试验2 各测点时域波形Fig.7 Time domain waveforms at each measurement point of the underground excavation vibration test 2

图8 井下掘进振动1 ～4 组均方根归一化指数拟合Fig.8 Fitted graphs of the root mean square normalised index for underground excavation vibration groups 1 ～4

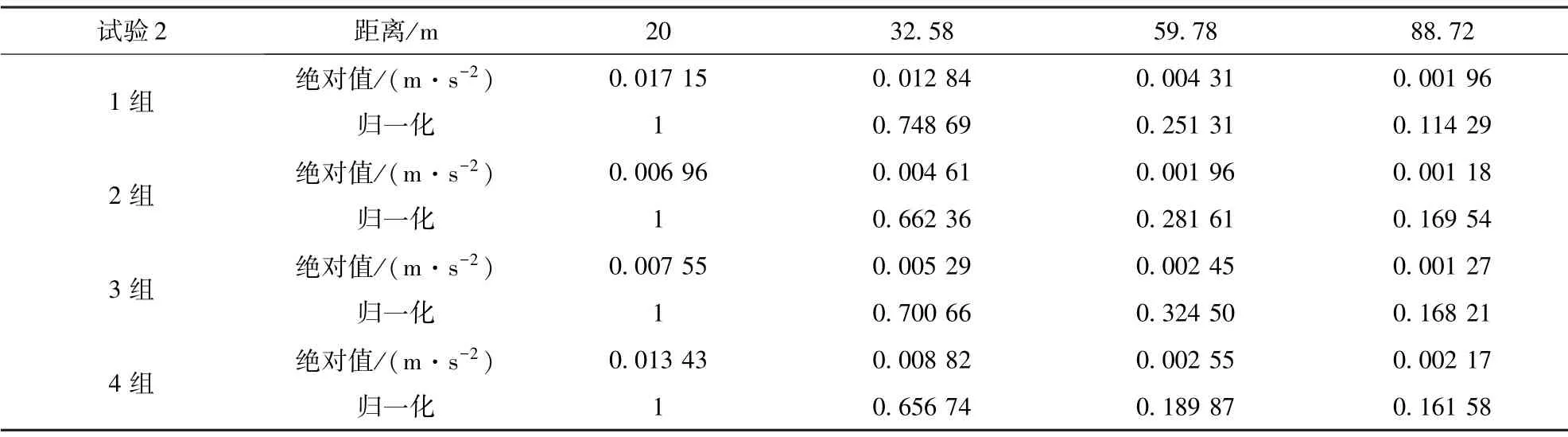
表3 井下掘进振动波有效值及有效值归一化Table 3 The effective value of underground excavation vibration wave and its normalization

3.3 掘进振源到气井水平距离预警模型

通过钢管振动试验及井下现场掘进试验,分别说明振动监测在天然气井段和煤层段都是可行的。将天然气井段和煤层段振动监测合并后,认为气煤防碰撞振动监测是可行的。 振动波在天然气井及煤层中的传播衰减规律都符合振动衰减数学模型通式A=A0e-αr,据此可分别列出天然气井段和煤层段的振幅均方根值衰减计算公式如下:

天然气井段:

煤层段:

化简可得

式中,E1为地面监测到的振幅均方根值,g;E2为掘进机产生的振幅均方根值,g;E3为掘进机振动沿煤层传到气井处的振幅均方根值,g;α1为振动在气井中的衰减系数,m-1;α2为振动在煤层中的衰减系数,m-1;L为煤层到监测点的垂直距离,m;X为掘进机到气井的水平距离,m。

计算公式(1)至(4)中的各项参数都可以根据现场实际情况得到,最终可计算出掘进机到天然气井的距离,从而实现防碰撞监测预警的目的。 由于在不同介质、不同环境中振动波的传播衰减系数均不相同,因此应用推导公式前需要进行现场试验,以得到相应环境下各参数及振动波的衰减系数。

4 结 论

通过钢管敲击振动试验、井下现场掘进振动试验,对监测结果进行分析,得到如下结论:

(1) 采用均方根值(有效值)为特征指标,能够反映整个振动振幅的大小和强弱;对均方根值归一化处理(除以本次振幅最大值)可以消除振源不同对振动衰减规律的影响。

(2) 对振动信号加速度均方根值归一化后进行指数拟合,拟合结果R2均超过0.96,指数拟合效果较好。 从监测结果和拟合公式来看,振动衰减规律符合一般衰减规律公式A=A0e-αr,振动衰减速度先急剧减小,后缓慢减小。

(3) 振动监测在天然气井段和煤层段是可行的,通过振动监测可以实现防碰撞监测预警。 通过振动衰减公式反演推导出的防碰撞距离计算公式,为后续防碰撞监测预警提供参考。