列车振动对岩溶区覆盖层内土洞稳定性影响机制
吴诗, 高旭, 陈阳
(中国地质大学(武汉)工程学院, 武汉 430074)
岩溶区覆盖层中土洞大量发育,土洞的失稳将威胁穿越该岩溶区的铁路交通正常运行[1-3]。开展列车振动对既有土洞稳定性影响机制以提出有效监测建议对其防灾减灾有重要工程意义。
国内外学者对岩溶土洞稳定性问题进行了大量研究。熊启华等[4]通过负压吸蚀论与潜蚀论建立力学模型给出土洞形成的临界地下水降幅以及岩溶区稳定性系数的数学表达式,并通过实例进行验证;靳红华等[5]利用强度折减法确定了黏聚强度和内摩擦角的折减系数,获得了岩溶覆盖区盖层土体的稳定系数计算式与塌陷坑稳定性判据系数;苏添金等[6]利用极限平衡理论对福建永定樟坑覆盖型岩溶土洞进行稳定性评价,并采用FLAC3D对土洞发育过程进行模拟,得出地下水下降对该岩溶塌陷作用最明显并给出临界水位降幅;苏永华等[7]运用FLAC3D依据突变理论建立地表塌陷分析判据,以此得到临界孔洞半径与地表塌陷范围。然而,这些研究都只考虑地下水或土洞形态对土洞稳定性造成的影响,忽视了列车振动的作用。
为了进一步研究振动荷载对土洞稳定性的影响,周捡平等[8]运用Abaqus软件结合动三轴试验提出土体中的累积塑性应变随深度逐渐减小,列车荷载的深度影响范围不随列车作用次数而增加;高程鹏[9]提出振动荷载下土洞稳定性与土体最大粒径、不均匀系数以及顶板厚度有关,最大粒径与不均匀系数越小、顶板厚度越大,土洞动力稳定性越强;肖先俊[10]通过FLAC3D进行模拟,得出顶板厚度较小时,埋深对土洞稳定性影响较大,极限承载力提高的贡献量随着顶板厚度的增加而减小;宋国壮[11]认为增大铁路路堤填筑高度可以降低溶洞顶板的竖向动变形,但同时会加剧溶洞发育区域上方路基表面的不均匀沉降,影响线路的纵向平顺性。唐万春[12]通过ANSYS软件对厚覆盖型岩溶路基列车荷载动力响应进行了数值模拟,提出当土洞顶板厚度相对跨度较大时,塑性区主要表现为拉剪屈服并首先出现在路基边缘;程星等[13-14]对振动时铁路旁土层产生的振波进行了研究,指出振波具有脉冲波的波形特征,且振压随距离呈非线性衰减,并提出致塌力未必会直接导致土层破坏,其机制与耦合效应及破坏累积效应有关。以上研究都对列车振动作用下的土洞稳定性进行了探讨,但都仅仅采用数值模拟手段,而没有经过物理模型试验的验证,且对土洞失稳可监测的敏感性指标研究不够。
鉴于此,现将依托武汉市江夏区乌龙泉岩溶塌陷实例,开展物理模型试验,探究列车振动荷载对覆盖层内土洞稳定性的作用机理,并用数值模拟分析其应力应变特征,据此提出有效监测建议。
1 模型试验原型
岩溶地面塌陷发生在乌龙泉矿区东侧,吉港水泥有限公司西侧京广线1 241+070东侧15.3 m,贺纸公路西侧26.0 m处,塌陷位于乌龙泉垅岗状地带,垅岗冲沟发育,地表高程90~100 m,相对高差最大可达10.0 m,发现两处陷坑,如图1所示。1#陷坑处为一近南北向水沟,沟宽6.0~7.0 m,沟水由南向北流,地势相对低洼;坑东侧为贺纸公路,高出陷坑处约2.0 m,坑西侧为京广铁路,高出陷坑处约2.0 m。塌陷处地表为Q2中更新统棕红色网纹状黏土覆盖,厚5.0~7.0 m。下伏基岩为碳酸盐岩,据井孔资料坑西侧井孔施工时,揭露有溶洞。
根据调查,乌龙泉岩溶地面塌陷主要有两方面因素,一是矿区井孔抽水使地下水动力条件剧烈变化所形成的真空负压吸蚀作用导致覆盖层内产生大量土洞;二是京广铁路列车运行对土洞产生振动破坏。现仅从第二方面因素来研究其岩溶塌陷机理,即仅考虑振动荷载对既有土洞稳定性的影响机制。
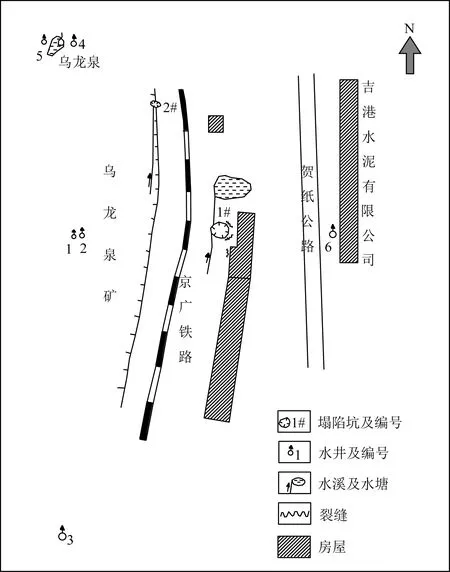
图1 乌龙泉岩溶塌陷平面示意图Fig.1 Plane diagram of Wulongquan karst collapse
2 物理模型试验
2.1 列车振动荷载作用相似性设计
相似理论中π理论认为:“当一个现象有n个物理量,且这些物理量中含有k个物理量的量纲是相互对立的,那么这n个物理量可以表示成相似准则π1,π2,…,πn-k之间的函数关系”[15],即
f(π1,π2,…,πn-k)=0
(1)
对于土工动力模型试验来说,动力响应中一般采用等效线弹性模型来考虑土体的非线性特征。主要需要考虑的物理量相似有模型和原型之间的几何相似性L,质量相似性M,时间相似性T,材料的密度ρ、动弹模量E、泊松比ν以及阻尼比D相似,动位移s、速度v及加速度a相似,应力σ、应变ε相似等。依照π定理可以写为
f(L,M,T,ρ,E,ν,D,s,v,a,σ,ε,…)=0
(2)
综合考虑试验模型箱尺寸、模拟范围、边界影响范围及设备加载要求,最终确定试验几何相似比为1∶10,质量密度相似比为1∶1,加速度比为1∶1。主要变量的相似比见表1。
2.2 试验装置及监测布置
考虑到周期性振动模型试验过程中边界反射效应对试验结果干扰影响,采用如图2所示的长宽高尺寸为2.6 m×1.6 m×1.1 m的模型箱。模拟列车振动荷载加载装置由激振器、信号发生器、功率放大器以及固定支架4部分组成。信号发生器提供激振器所要的激励信号源,功率放大器将其进行功率放大后转换为具有足够能量的电信号,驱动激振器工作。摄像机在模型箱左上角全程记录地表塌陷过程。
模型试验监测布置如图3所示,包含土压力监测、地表沉降和地表倾斜监测3个部分。位移和倾斜角测量器布置于地表,而土压力监测则环绕土洞布置,共7处,平均每处距离土洞壁约10 cm,且左右对称分布。其中代号sp5监测水平向土压力,其他6处土压力则监测竖直向土压力。

表1 试验最终选取的参数相似比Table 1 Similarity ratio of parameters finally selected in the test

图2 列车振动荷载岩溶塌陷模型正视图Fig.2 Front view of karst collapse model under train vibration load

图3 列车振动荷载岩溶塌陷监测装置布置示意图Fig.3 Layout of karst collapse monitoring device under train vibration load
2.3 试验步骤
根据乌龙泉岩溶塌陷实例覆盖层结构可知覆盖层为单一老黏土层,层厚约5 m。本试验相似比为1∶10,即要填筑50 cm厚相似材料,相似材料仍采用该区老黏土,具体天然土体与相似材料物理力学参数见表2。填筑覆盖层前,先将40 cm×40 cm×40 cm的方形泡沫块削至图4所示形状,放在模型箱底板开口处。开始试验时,从模型箱下方开口将泡沫块掏至合适大小。
待覆盖层填筑完毕后,在土体表面距土洞50 cm位置处放置一上宽17 cm、下宽30 cm、长约50 cm、高10 cm的梯形钢槽,在其中填满粗砂以模拟铁路路基(图5),在路基上方架设列车荷载加载装置。
根据文献[16]可知,列车振动波形可简化为正弦波,其振动频率根据列车速度和单节列车长度计算可得列车常用振动频率见表3。通过文献可得列车实际应力为60 kPa,按相似比换算后得到相似应力即试验振幅为6 kPa。试验时,通过实时观察并调整功率放大器电流旋钮使路基位置处sp13土压力监测值到达6 kPa,以契合相似后实际列车行驶下的振幅。将列车荷载加载装置按设定频率加载,每次振动5~15 min,以探究列车振动频率对土洞稳定性影响机制。

表2 天然状态下土体及相似材料物理力学性质指标Table 2 Physical and mechanical properties of natural soil and similar materials

图4 模型填筑前土洞模拟Fig.4 Simulation of soil hole before model filling

图5 路基铁轨示意图Fig.5 Schematic diagram of subgrade rail

表3 列车CRH380AL常用振动频率换算表Table 3 Common vibration frequency conversion table of train CRH380AL
2.4 试验结果分析
如图6所示是土洞周围土压力监测曲线以及地表沉降及倾斜角监测曲线,时刻为试验时记录的时间。
在22:25时刻之前,从图6(a)、图6(b)和图6(c)所示土压力监测曲线可知,在受力状态突然改变的瞬间(如开始振动、停止振动时)会有骤降,之后土压力会缓慢回升。从图6(d)所示地表沉降曲线与倾斜角曲线可以看出,在22:25之前,地表沉降、与倾斜角都变化不大。该阶段称为覆盖层初始振动损伤积累阶段。
在22:25—22:44,如图6(d)可以看到这一组试验时地表沉降与倾斜角变化逐渐加快。如图6(a)两个大小圆圈所示的sp4曲线出现先上升再下降的变化规律,随后sp7曲线同样出现先升再降趋势,说明靠近sp4附近(其位置如图3所示)土洞顶板先出现应力状态调整,由此造成图7所示背离振源方向一侧地表裂缝先发育,而靠近振源一侧

图6 物理模型试验监测曲线Fig.6 Monitoring curve of physical model test
地表后发育裂缝现象。与此同时,代表土洞顶板中心水平土压力的sp5曲线如图6(b)所示出现呈下降趋势,说明此时土洞顶板弯曲变形,类似简支梁弯曲破坏,其底板出现拉张裂缝[图8(a)],并发展到出现掉土现象[图8(b)]。该阶段称为临界塌陷阶段。
从22:57开始7 Hz的再一次振动,经过一段时间振动后,水平向土压力sp5骤降,地表沉降迅速增加,裂缝迅速扩展至贯通,顶板被拉坏,该阶段称为加速变形至塌陷阶段。根据图9可知,塌陷坑近圆形,直径约47 cm,拉张裂缝宽1~2 cm。值得注意的是,布置在中层和深层的土压力一直都没有明显变化现象。

图7 塌陷演化过程中地表裂缝发育情况Fig.7 Development of surface fractures in the process of collapse evolution

图8 土洞顶板内部变形破坏现象仰视图Fig.8 Top view of internal deformation and failure of soil tunnel roof

图9 列车振动工况岩溶塌陷地表现象Fig.9 Surface collapse phenomenon of karst under train vibration condition
3 数值模拟
3.1 数值模型构建
数值模拟主要采用有限差分软件FLAC3D进行分析。为了能够更好地针对列车振动工况下的塌陷情况进行分析,选择三维数值模拟。根据实际原型尺寸进行建模,即黏土层厚度5 m,基岩2 m,为尽量避免边界效应长度取26 m,如图10所示。覆盖层中按物理模型试验观测的土洞高跨比设置为洞宽5 m,高4 m。铁路路基按物理模型1∶20进行还原,即上底3.4 m,下底6 m,高2 m。

图10 数值模型构建Fig.10 Construction of numerical simulation model
列车振动动力响应分析关键在于如何施加列车振动荷载、设置边界条件以及选择合适的阻尼类型、阻尼参数。模拟考虑的荷载为岩土体自身的重力及列车振动荷载。根据前文确定的振幅与频率,得出列车振动荷载表达式为
F=3×104×[1-cos(4.4πt)]
(3)
边界条件方面,采用FLAC3D提供的静态边界来吸收波以减少边界上波的反射。静态边界是通过在模型的法向和切向设置自由阻尼器来实现入射波的吸收。因此,模型侧面与底面设计为静态边界,地表设置为自由边界。
设置阻尼方面,阻尼主要源自材料的内部摩擦及可能存在的接触表面滑动,FLAC3D提供了3种阻尼形式:瑞利阻尼、局部阻尼和滞后阻尼。选用瑞利阻尼,需要确定最小中心频率ωmin和最小临界阻尼比ξmin两个参数。最小中心频率ωmin一般为22.8 Hz,最小临界阻尼比ξmin经验值一般为0.05~0.2,取0.05。
根据开展的试验以及查阅相关的勘察资料,确定了数值模拟计算所用的岩土体的相关参数,如表4所示。参考文献[14],将路基与老黏土层设为摩尔-库伦模型,基岩层设定为弹性模型。
动力破坏的数值模拟分两步进行,首先是静力计算至平衡状态,其次是在此基础上再加动力荷载。

表4 岩土体物理、力学参数Table 4 Physical and mechanical parameters of rock and soil mass
3.2 数值模拟结果分析
由图11可知,静力计算条件下,土洞上方出现局部塑性区(红色为剪切破坏,绿色为张拉破坏),最大剪应变率值维持在低水平。此时洞顶最大位移约为6 cm。符合物理模型试验土洞开挖后出现较小地表位移,周围存在局部破坏,但土洞尚处于整体稳定状态不致破坏的情况。
在静力基础上,在铁路路基顶部正中施加振幅60 kPa竖向正弦动荷载,并对照物理模型试验中土压力盒位置布设相应监测点。得到破坏时动荷载下土压力监测图(图12)、最大剪应变率云图与竖向位移云图(图13)以及不同时步下塑性区(图14)。

图11 静力条件下数值模拟Fig.11 Numerical simulation under static condition

图12 动荷载作用下浅层土压力监测曲线Fig.12 Shallow earth pressure monitoring curve for dynamic load calculation
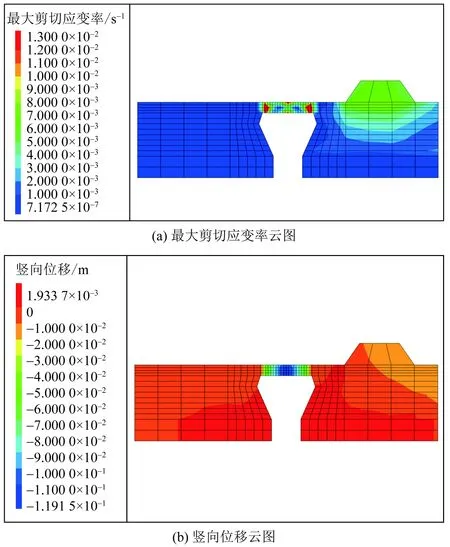
图13 动荷载作用下塑性区和竖向位移云图Fig.13 Plastic zone and related cloud diagram of dynamic load numerical simulation

图14 动荷载作用下计算塑性区Fig.14 Calculated plastic zone under dynamic load calculation
由图12(a)可以看出,30 000时步之前,路基地表处布置的竖向土压力监测sp13计算尚不稳定,即还未按给定正弦动荷载施加力。30 000步后计算逐渐稳定,此时,图12(b)中浅层水平向拉力大幅度增加,图12(a)中浅层竖向土压力sp4与sp7出现两次先增后减的波动,第一次波动时sp4的增幅要明显比sp7大,第二次波动sp4与sp7增幅相近。该现象与物理试验临界塌陷阶段开始时sp4、sp7与sp5产生的趋势一致。之后sp4、sp7与sp5曲线趋于稳定。当时步达到215 000步左右时,图13(a)中土洞顶部高剪应变率区(红色区域)已贯通,可以判断此时模型已发生塌陷。根据图13(a)与图13(b)可以得出塌陷直径大约4.4 m,与物理模型中实际塌陷换算后4.7 m相近。
观察塑性区随时步变化图(图14)发现,动荷载作用下塑性区继承了土洞顶板下部为拉破坏,上部为剪破坏的特性;背离路基一侧洞顶周围出现部分拉破坏,洞肩周围出现剪破坏,且洞肩周围的剪破坏随着振波和反射波的累积逐渐加宽;靠近路基侧的土洞顶板周围虽然在计算中也出现了拉破坏塑性区,但面积很小,且随着计算收敛而消失。符合物理试验中土洞背离路基侧周围较另一侧早出现裂缝,且裂缝发育更明显的现象。
4 结论
采用物理模型试验的方法研究了列车振动作用下土洞土压力与位移动力响应特征,并用数值模拟的方法对其进行应力应变特征分析与验证。对工程中受列车荷载影响的岩溶区覆盖层内土洞稳定性监测预警工作有以下几点启示。
(1) 根据物理模型实验的浅层土压力和中、深部土压力监测曲线可知,浅层土压力的动力响应较中、深层更为明显。实际工程中布设土压力监测点时应增加浅层土压力监测点,中、深部可以少布置甚至不布置。
(2) 通过对浅层竖向土压力的曲线分析得知,在临界塌陷阶段,土洞两侧会出现竖向土压力先增加后减小的变化规律,且背离路基侧土洞土压力变化幅度更大。实际工程中应更关注土洞背离路基侧竖向土压力响应。
(3) 列车振动作用下土洞破坏模式:背离路基侧洞肩出现大面积剪破坏,而土洞顶板附近为拉破坏。监测中应重点关注土洞背离路基侧地表拉裂缝发育情况。

