起下钻引发的环空瞬态波动压力计算方法
赵岩龙, 任传杰, 冯智, 祝宏平, 米翔, 尹俊轩
(1.中国石油大学(北京)克拉玛依校区石油学院, 克拉玛依 834000; 2. 中国石油大学(北京)石油工程学院, 北京 102249;3. 中国石油天然气股份有限公司新疆油田分公司石西油田作业区, 克拉玛依 834000)
目前,油气勘探领域不断向更加深部的复杂地层进发,泥浆密度窗口通常较窄,在钻进过程中容易产生“卡、塌、漏、喷”等现象[1-2],准确计算井筒波动压力对保障钻井作业安全具有重要意义。1977年,Lubsinki等[3]首次提出钻井流体的流动过程是瞬时变化的,从此开启波动压力瞬态计算的序幕。随后国外学者针对瞬态波动压力的求解与计算开展了大量研究[4-6]。国内,钟兵等[7]采用混合隐式特征线法对瞬态压力波动压力控制方程组进行数值求解,计算精度及速度得到了进一步提高。周开吉等[8]通过对瞬态波动压力敏感因子分析,提出一种新的预测模型。樊洪海等[9]基于钻井流体不稳定流动为条件,建立了井筒波动压力预测模型。韩付鑫[10]基于流体流动为一元流动,建立了井筒瞬态波动压力的计算模型。周号博[11]针对控压钻井气侵过程进行分析,建立了井筒气液两相流模型,并对井筒回压进行求解。张智等[12]基于水锤效应理论,建立了高产气井瞬时关井过程的井筒瞬变流数学模型。以上模型均未对起下钻过程中产生的井筒波动压力进行详细的分析。由于起下钻过程中产生的瞬态波动压力对于井筒安全具有重要的作用,亟须开展相关研究。
钻井起下钻过程中井筒内产生的波动压力不可忽略,在进行起下钻作业时,井筒内的流体将由静止或稳定流的状态过渡到不稳定流动状态,此时,井筒流道内各点流体的流速、钻井液的结构力、流道的流通状态、井筒压力都随之发生变化[13-16]。现针对起下钻过程中井筒波动压力,考虑流体与管柱的弹性对压力波传播的影响,开展井筒瞬态波动压力计算与影响因素分析,对现场起下钻作业具有指导意义。
1 瞬态波动压力数学物理模型建立
1.1 瞬态波动压力物理模型
可将钻井井筒流动系统划分为3个流道:①从管柱底部至井口的环空流道,记编号为Ⅰ,流道内流体流量为Q1,压力为p1;②从管柱底部至井口的管柱内部圆形流道,记编号为Ⅱ,流道内流体流量为Q2,压力为p2;③从管柱底部到井底的圆形井底流道,记编号为Ⅲ,流道内流体流量为Q3,压力为p3。流道物理模型结果如图1所示。
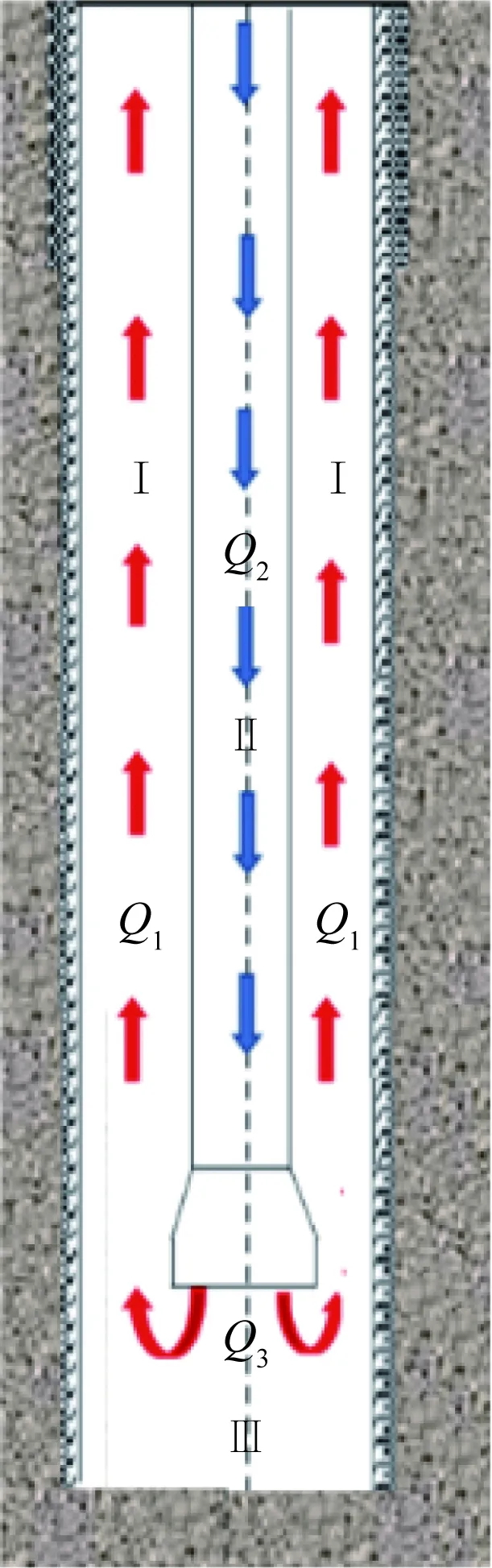
图1 井内流道分析示意图Fig.1 Schematic diagram of flow channel analysis in the well
1.2 瞬态波动压力数学模型
在建立瞬态波动压力数学模型时,基于以下基本假设。
(1)将钻井流体在流通通道中的三维流动视为一维不稳定流动。
(2)流道内的流体和井筒为线弹性的,所受应力与应变服从正相关。
(3)忽略已下套管处固井水泥和地层对套管弹性的影响。
1.2.1 连续性方程
在井筒流道中,取任意长度为dz的微元控制体,控制体横断面分别为1-1和2-2,如图2所示;钻井流体从断面1-1流入,经过控制体,从断面2-2流出,控制体长度为dz,设过水断面A和钻井流体密度ρ是时间和空间的函数,即A=A(z,t)、ρ=ρ(z,t),断面1-1处面积设为A,流体的密度为ρ,流速为v。
dt时间段内,控制体内的质量变化量应等于流入与流出控制体的质量差,根据质量守恒定律,可得连续性方程为
(1)
式(1)中:A为断面截面积,m2;ρ为流体密度,kg/m3;ν为流体速度,m/s。
由式(1)及A=A(z,t)、ρ=ρ(z,t),可得
(2)
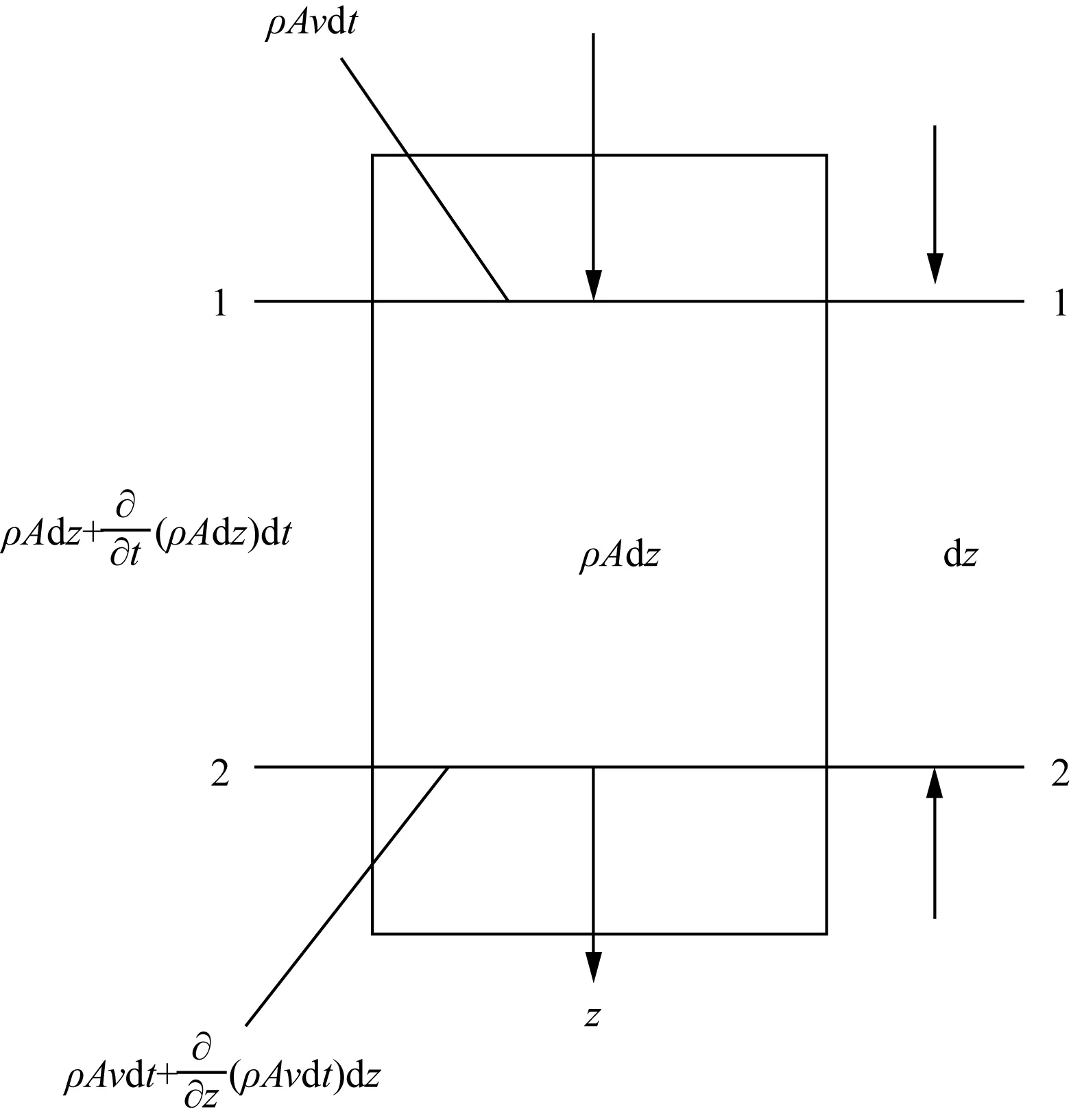
图2 连续性方程控制体示意图Fig.2 Schematic diagram of the control body of the continuity equation
(3)
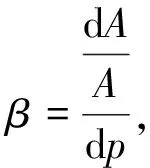
(4)
因为压力p是井筒空间位置z和时间t的函数,即p=p(t,z),将p对时间t的全微分形式代入式(2)并两边同时除以(α+β)可得
(5)
压缩系数与压力波速之间的关系[15]为
(6)
式(6)中:c为压力波传播速度,m/s。
将埃利维(Allievi)定理dp=ρcv0代入式(5)可得
(7)
式(7)中:z为轴向位置,m;t为时间,s。
1.2.2 动力方程
在水力系统中任意位置取一长为dz的微元控制体,流体从断面1-1流入控制体,经断面2-2流出。其中,流道横截面积A和流体压力p是空间位置(z)和时间(t)的函数,即A=A(z,t),p=p(z,t),如图3所示。
对微元控制体在z方向上进行受力分析。
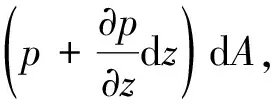
记v为沿着z方向的流速,针对不稳定流,根据牛顿第二定律∑F=ma,可得单位质量流体的动量方程为
(8)
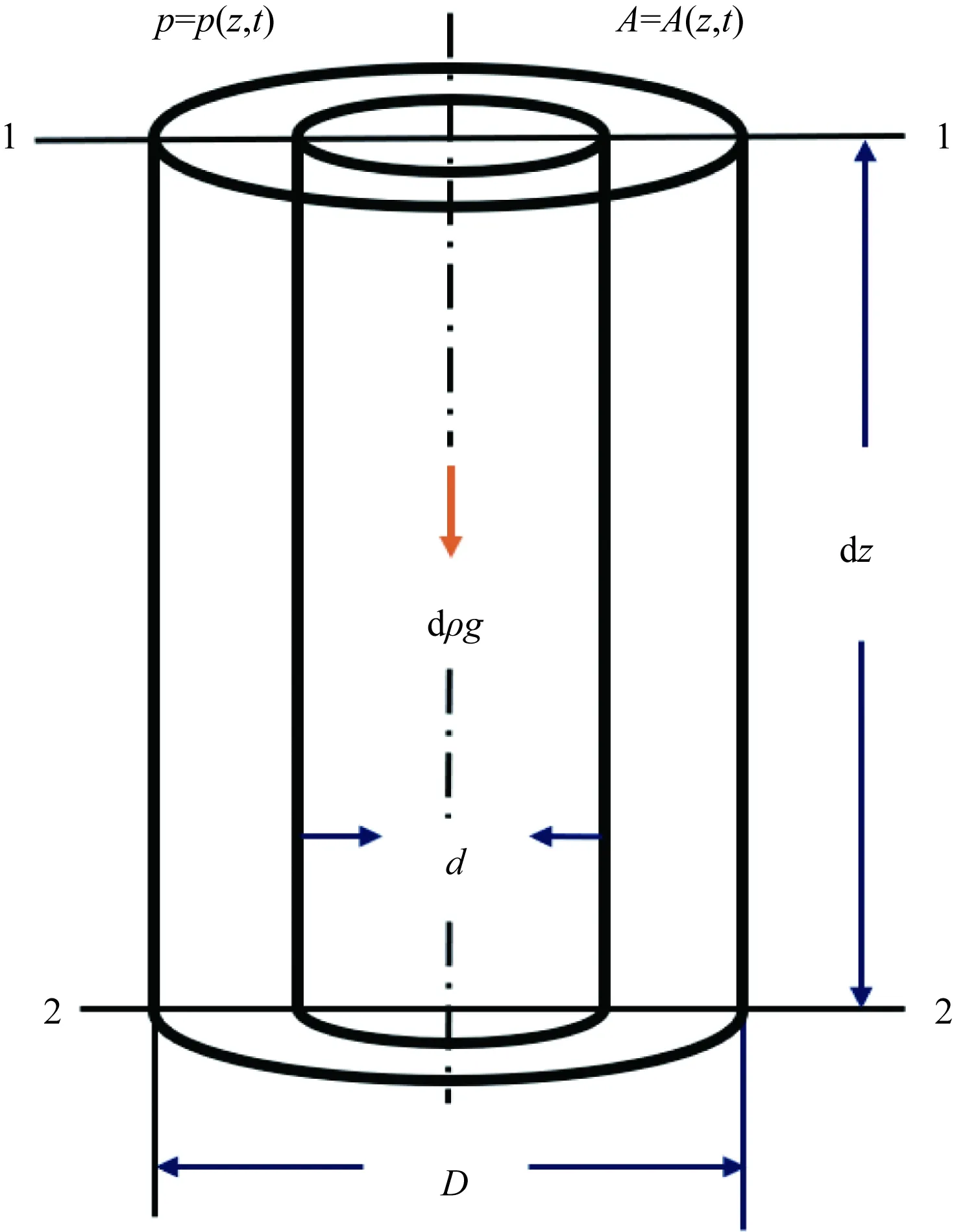
图3 流道内流体微元控制体示意图Fig.3 Schematic diagram of the fluid micro-element control body in the flow channel
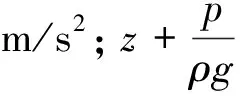
(9)
2 起下钻时井筒波动压力求解
为方便后续计算,用测压管水头压头H替代压力p,代入瞬态波动压力连续性方程(7)则有
(10)
因此,起下钻时井筒瞬态波动压力的连续性方程为
(11)
式(11)中:v为流体的速度,m/s;c为压力波传播速度,m/s。
(12)
式(12)中:f为范宁摩阻系数;D为管径,m;τ为壁面切应力,Pa。
2.1 特征线法求解
对开关泵时瞬态井筒波动压力控制方程-连续性方程[式(11)]和动力方程[式(12)]进行变形可得
(13)
(14)
引入系数λ对式(13)和式(14)进行线性化可得
(15)
由多元微分法则可知,测压水头和流速对时间的全导数为
(16)
(17)
令
(18)
则式(15)为
(19)
对式(18)进行求解,可得
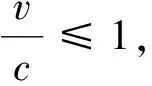
特征式化转换成常微分方程为
(21)
分别用向前特征线C+和向后特征线C-表示为
(22)
(23)
利用有限差分对上述方程进行求解,首先将时间t和空间z进行离散化处理,时间t被划分成若干个Δt,空间z被划分成若干个Δz,且Δz和Δt满足dz/dt=c,此时就可得到一个关于时间和空间的z-t平面网格[12,18]。平面上的任意点的压头H和速度v具有唯一值。将R看做原点,过R作向前特征线,将S看作终点,过R作向后特征线,两条曲线相交于点W,如图4所示。
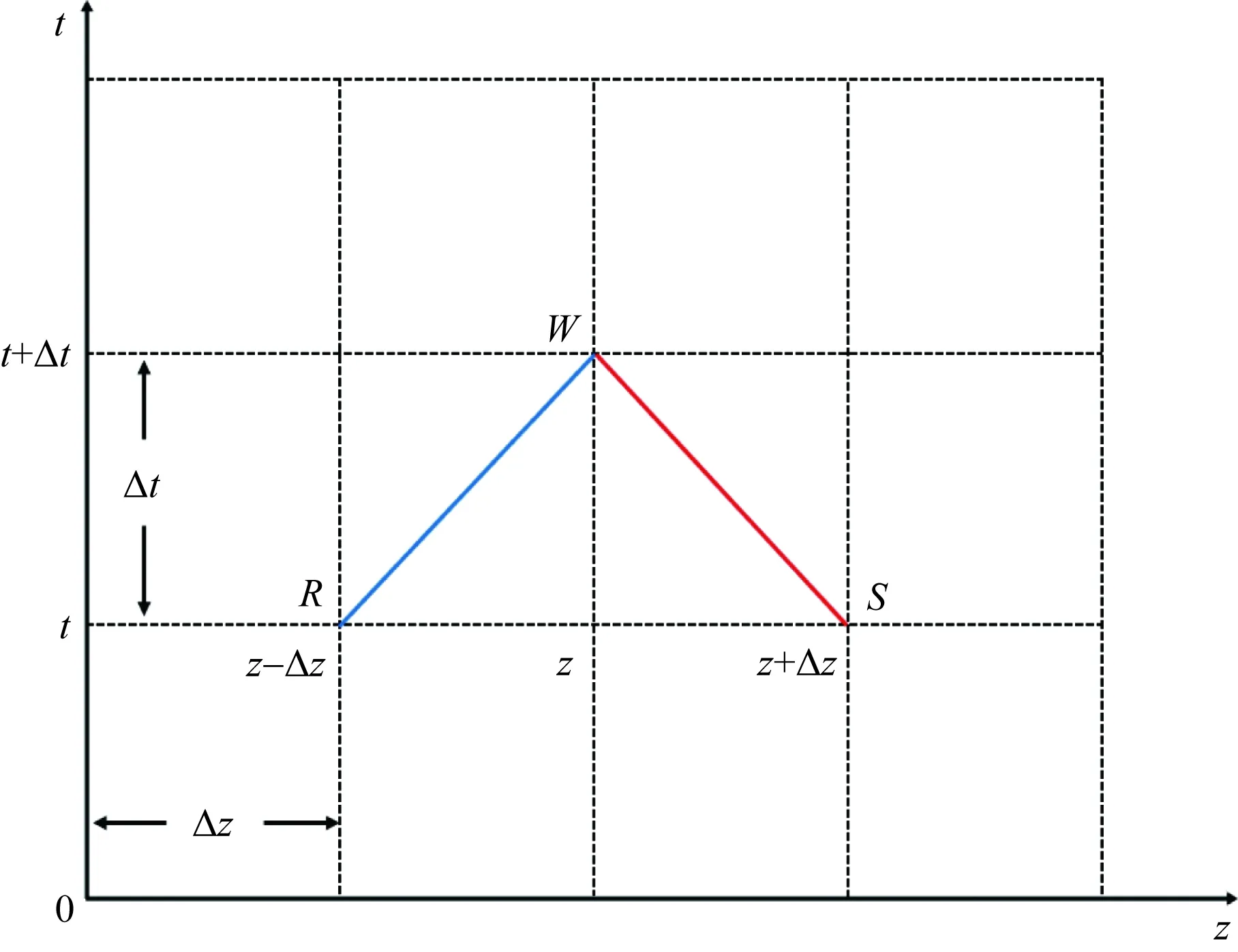
图4 z-t网格示意图Fig.4 Schematic diagram of z-t grid
式(22)和式(23)可化为
(24)
(25)
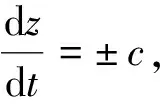
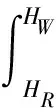
(26)
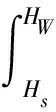
(27)
式中:HW为t+Δt时刻W点的压头;HR为t时刻R点的压头;HS为t时刻S点的压头;vW为t+Δt时刻W点的流速;vR为t时刻R点的流速;vS为t时刻S点的流速;zW为t+Δt时刻W点的位置;zR为t时刻R点的位置;zS为t时刻S点的位置。
由于v与z的函数关系未知,因此对其作近似处理,近似处理结果为
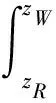
(28)
式(24)和式(25)沿向前特征线C+和向后特征线C-可表示为
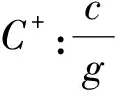
(29)
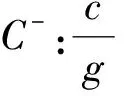
(30)
联立式(29)、式(30)可得HW和vW。
2.2 定解条件
由于井筒瞬态波动压力方程为偏微分方程,在求解过程中由于没有明确的解析解,故需给定初始条件、边界条件进行数值求解。根据现场实际工作条件,在起下钻过程中,可将流道视为在关泵状态下的堵口管。
初始时刻,井筒环空中的钻井液流量即为由于钻井液黏附钻杆运动所产生的流量。若不计大气压力,则井筒环空流道上边界压力为0,则在任意时刻井筒内的上边界条件为
(31)
3 实例计算及影响因素分析
3.1 模型验证
1974年Clark等[19]针对Utah一口井的下钻过程进行波动压力数据测试。该井井眼尺寸及钻井液物理属性如表1所示。为验证瞬态波动压力模型的准确性与适用性,采用Clark实验数据对该模型进行瞬态波动压力和稳态压力波动计算并与现场实测数据进行对比验证。
Clark实验模型中,井深4 654 m,下入长度为3 508 m直径为3-1/2 in的钻杆(1 in=0.025 4 m)、925 m直径为2-7/8 in的钻杆以及146 m直径为3-1/8 in的钻铤。井筒充满钻井液,钻井液采用宾汉流体,现计算套管鞋处井筒的波动压力。该井下钻过程中,不同时刻钻杆的运行速度如图5所示。
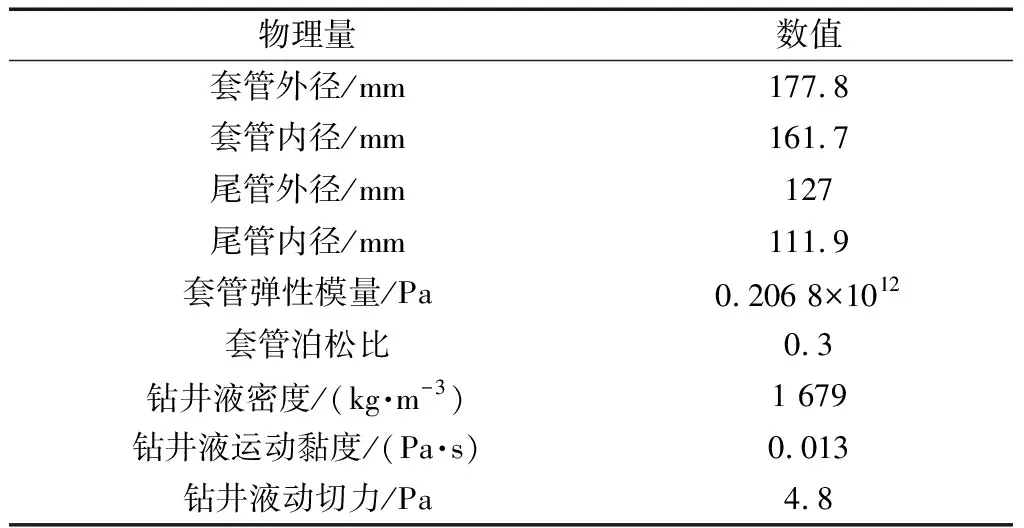
表1 井眼尺寸及钻井液物理特性Table 1 Wellbore size and physical properties of drilling fluid
针对该井在下钻过程中,套管鞋处的波动压力分别采用稳态波动压力和瞬态波动压力模型进行求解,结果如图6所示。套管鞋处稳态波动压力的最大值发生在11.30 s时,最大值为5.038 MPa;套管鞋处瞬态波动压力的最大值发生在11.30 s时,最大值为5.787 MPa。
由于钻杆速度发生变化而产生的波动压力需通过钻井液介质传递到套管鞋处,导致测量的钻杆速度计算出的流体的速度并非此时刻的真实流速。因此,计算理论值与实测值之间较大的时间滞后性是由于测量速度所引起的流体的流速变化存在时间滞后。
计算结果与实际测量值趋势基本相同,瞬态波动压力计算结果最大值误差小于5%;瞬态波动压力的值相对于稳态波动压力的值精确度更高,因此在实际操作过程中,根据瞬态波动压力的计算结果采用相关技术措施更能保证井筒的安全性能。
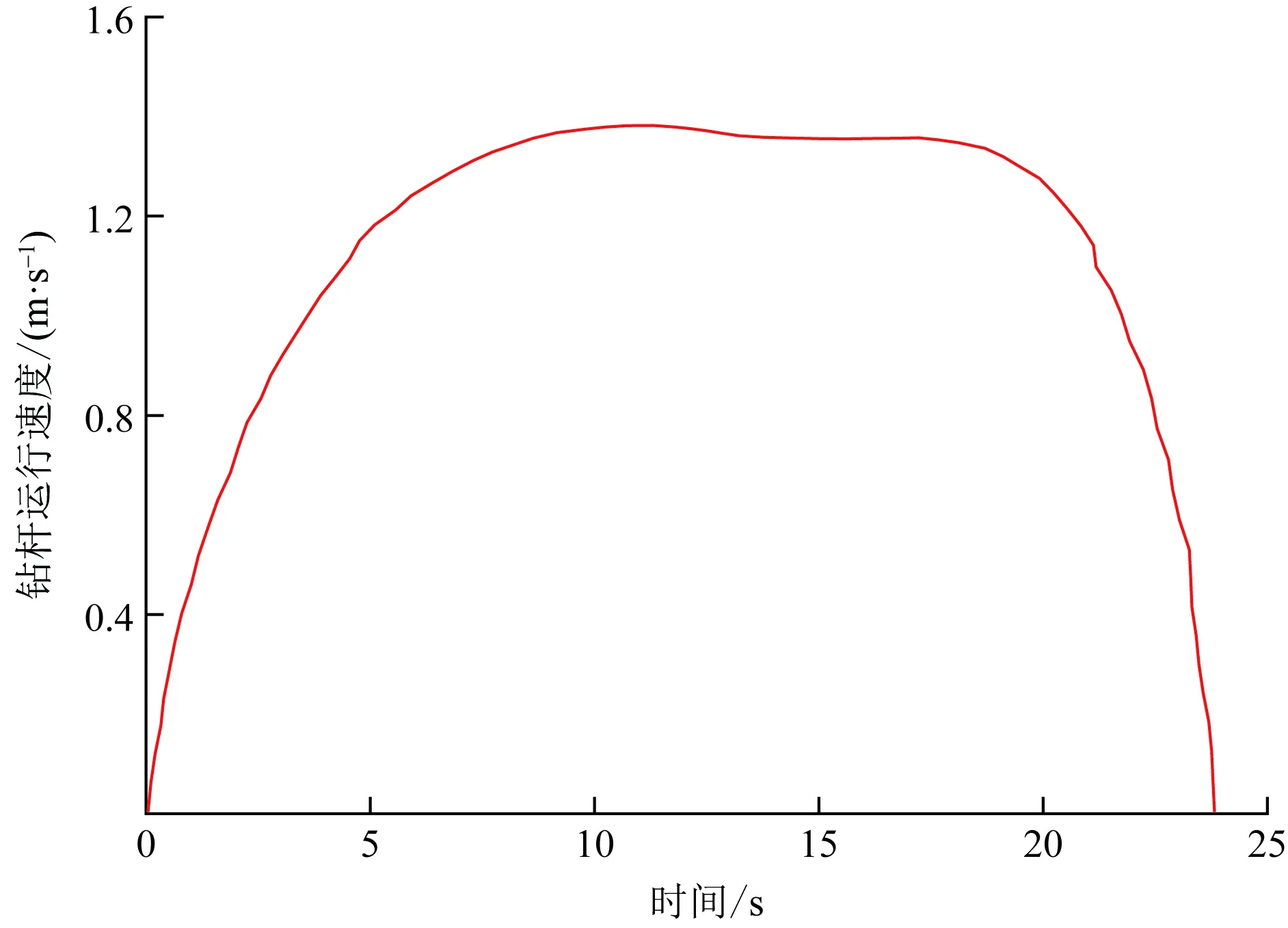
图5 钻杆运行速度Fig.5 Drill pipe operating speed
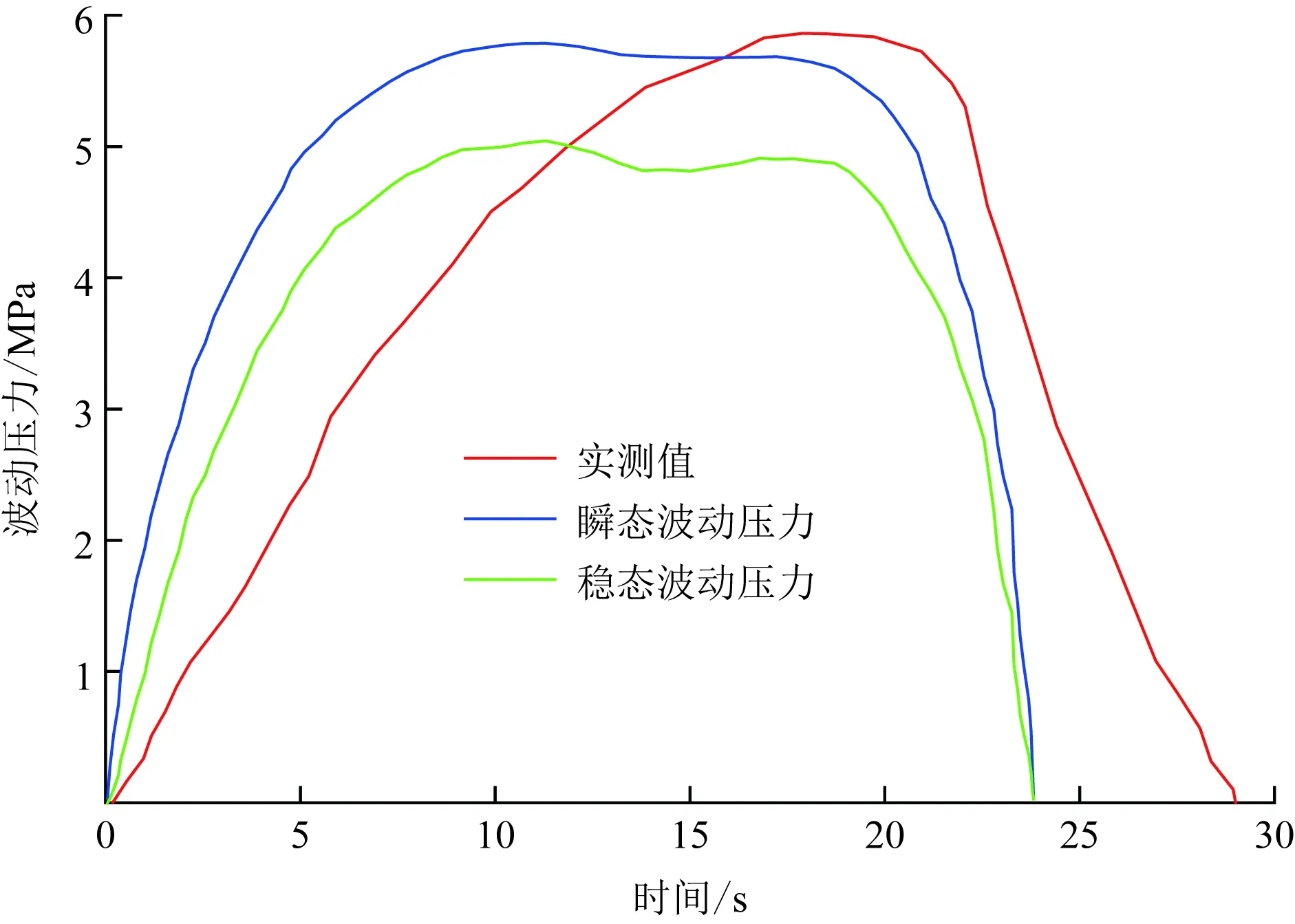
图6 Clark实验中压力波动理论值与实测值对比图Fig.6 Comparison of theoretical and measured pressure fluctuations in Clark experiment
3.2 敏感性分析
当钻杆以不同的速度进行下钻作业时,不同时刻的钻杆运行速度如图7所示;当钻杆分别以v1、v2和v3速度进行下钻时,套管鞋处的井筒瞬态波动压力结果如图8所示。
由图8可知,随着钻杆运动速度的增大,套管鞋处的井筒波动压力也随之增加。由于钻杆运行速度增大,导致井筒环空中流体的流速也随之增加,因此井筒环空中摩阻增大,进而环空中的压力产生更加剧烈的变化,导致套管鞋处的井筒瞬态波动压力增大。对于起下钻过程中,应当采取适当的措施,尽可能减小起下钻的速度,以防止由于波动压力过大对储层及复杂地层产生破坏。
不同的钻井液密度对于井筒环空的波动压力具有同样重要的意义。当在下钻过程中,井筒内的钻井液密度分别为1 679、1 879和2 079 kg/m3时,套管鞋处的波动压力分布如图9所示。随着钻井液密度的增大,瞬态波动压力也随之增大。因此,在保证井筒安全的前提下,可以考虑通过降低钻井液密度以减小环空中瞬态波动压力的影响。
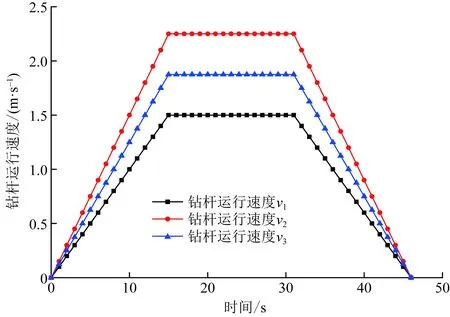
图7 不同钻杆运行速度图Fig.7 Diagrams of operating speed of different drill pipes
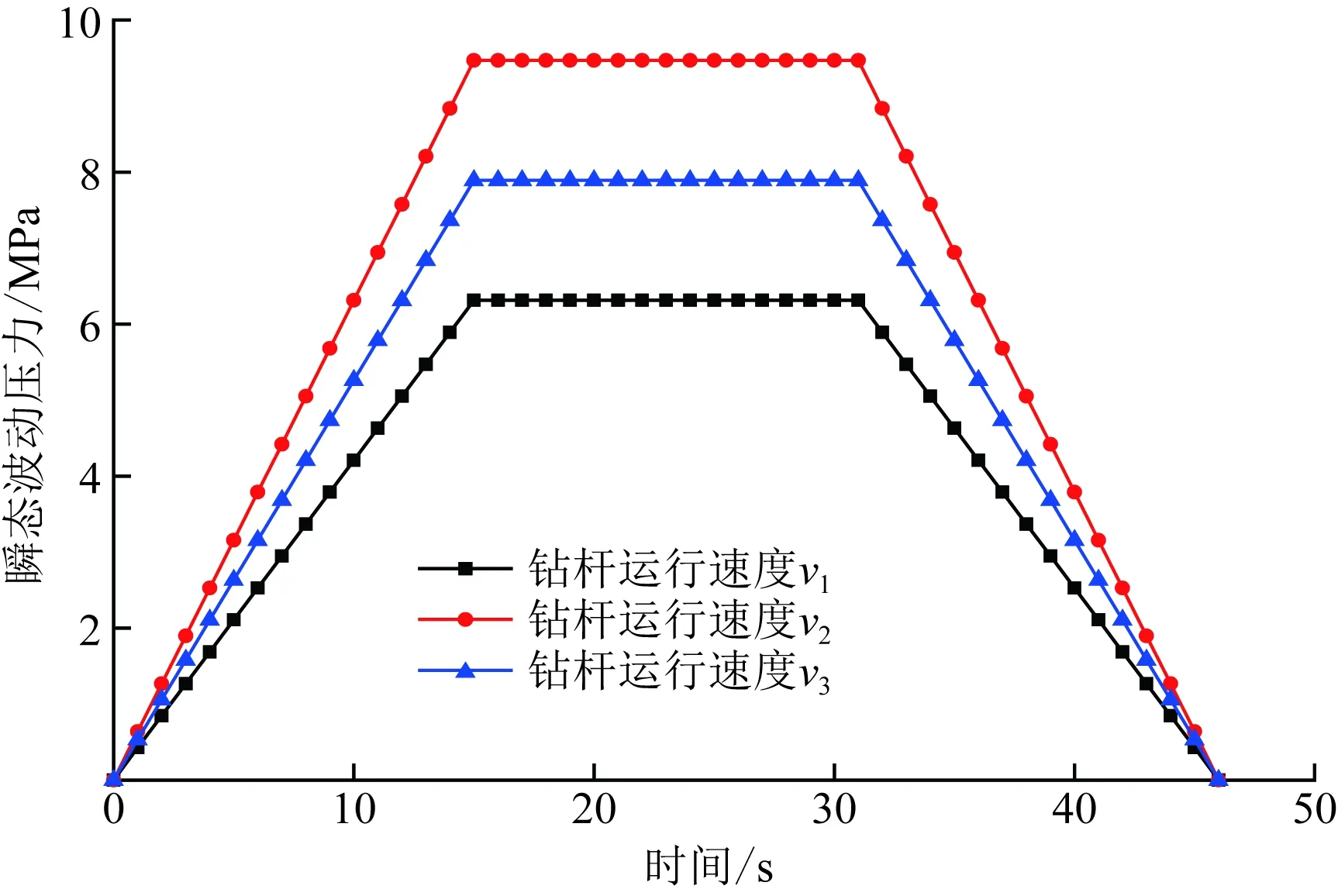
图8 钻杆运行速度对瞬态波动压力影响曲线Fig.8 Curve of influence of drill pipe operating speed on transient fluctuating pressure
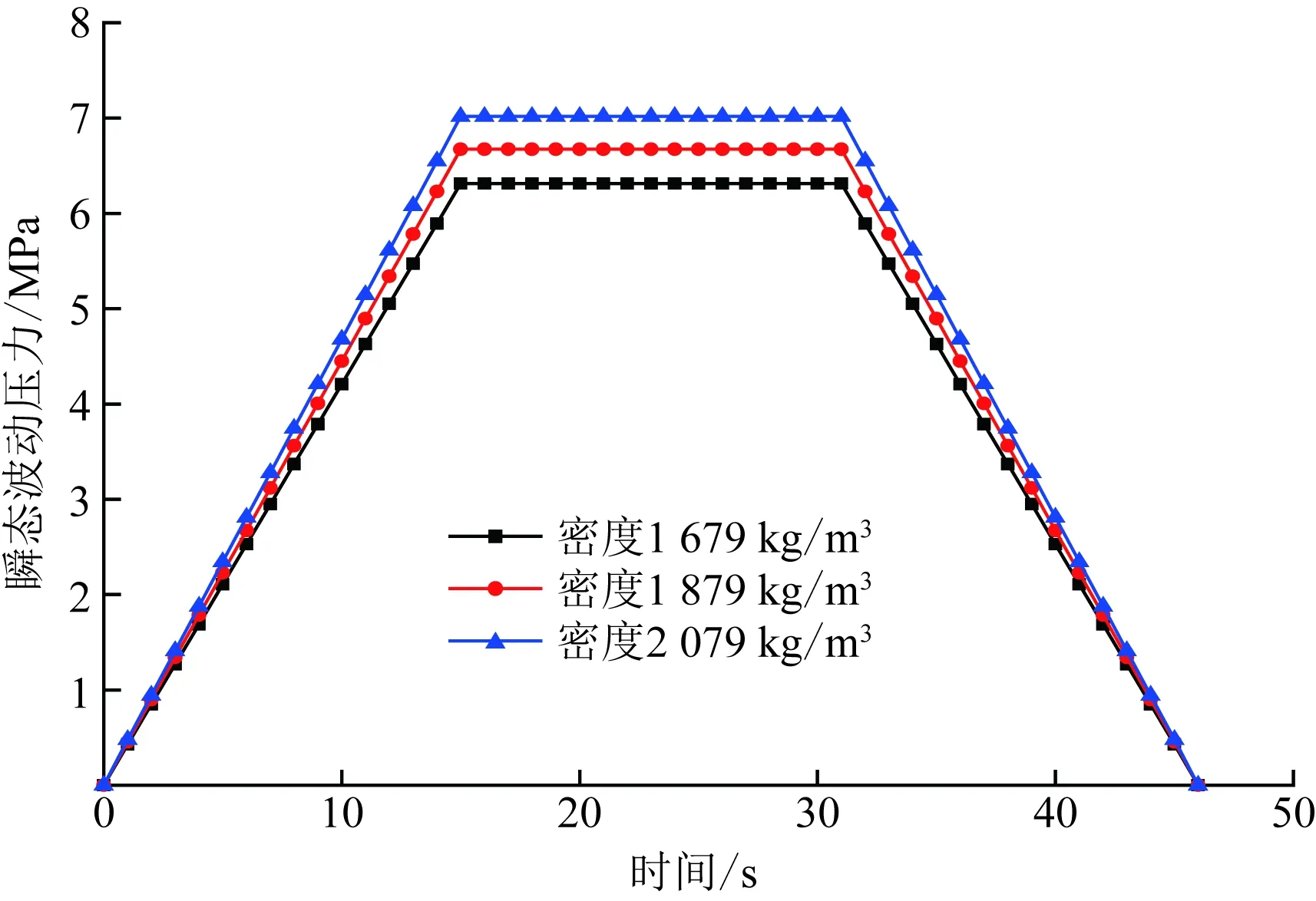
图9 钻井液密度对瞬态波动压力影响曲线Fig.9 Curve of influence of drilling fluid density on transient fluctuating pressure
5 结论
(1)基于流场流道分析,建立井筒环空瞬态波动压力计算模型,并采用特征线法进行数值求解,利用该模型可得到更加精确的环空波动压力值及波动压力的时间分布特征。
(2)钻井流体及井筒流道均具有可压缩性,压力波在传播过程中,以弹性波的形式在井筒流道内进行传播;随着钻杆运行速度的增加,环空中瞬态波动压力增加。
(3)现场钻井作业过程中,在保证钻井安全的前提下,可通过降低钻井液密度、减小起下钻速度以减小瞬态波动压力的影响。

