列车荷载下冻土路基非平稳随机振动分析的时域显式法

陈智锋， 李颖雄， 赖远明， 苏 成，4

（1.华南理工大学土木与交通学院，广东广州510640； 2.西南交通大学智慧城市与交通学院，四川成都611756；3.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000； 4.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640）

0 引言

我国为世界第三冻土大国，多年冻土面积占国土总面积的21.5%，其中高原冻土面积更是居于世界之最［1］。随着“一带一路”倡议深入推进实施，冻土区的铁路建设与维护得到高度重视。同时，国民经济的发展使得列车行驶频次有所提升，加之受全球变暖［2］等气候因素的影响，冻土区铁路病害问题越来越突出。为保障冻土区铁路的安全运营，亟须发展高效准确的计算方法，分析列车行驶对冻土路基动力响应的影响。

冻土路基在列车荷载作用下的动力响应是当前的研究热点之一。马巍等［3］和朱占元等［4］开展了列车荷载作用下冻土路基动力响应的现场监测研究，为列车通过冻土路段时路基稳定性的预测分析提供了实测资料依据。Stevens［5］、孔祥兵等［6］和李双洋等［7-9］采用数值分析方法，研究了一次行车荷载作用下路基的位移和应力等动力响应问题。此外，还有部分学者［10-13］进行了列车荷载作用下冻土路基的稳定性、蠕变、轨枕响应和车速对路基响应影响等方面的数值模拟研究。

上述研究中，都采用了确定性的列车荷载，选取某一次列车驶过产生的荷载样本计算路基响应，其结果难以反映铁路实际运行中由轨道不平顺及列车类型和轴重差异导致的荷载随机性［14］。对于路基的特定横断面，列车驶入和驶出的过程导致其顶部荷载的统计特征具有显著的时变特性。因此，在研究路基动力响应时应将其顶部列车荷载按非平稳随机荷载考虑［7，15］。由于冻土独特的物理、热力学性质以及非平稳随机振动分析的复杂性，目前关于随机列车荷载作用下冻土路基动力响应的研究较少。

目前，解决结构非平稳随机振动问题的主要方法有蒙特卡罗模拟法、虚拟激励法［16］、概率密度演化法［17］以及时域显式法［18］等。其中，时域显式法通过构建系统动力响应的时域显式表达式，在随机分析中可以针对任意关键响应进行降维，具有理想的计算效率，已成功应用于高层建筑［19］、大跨度桥梁［20］和车桥耦合系统［21］等大型复杂结构系统的随机振动分析。在随机振动分析中，若已知随机激励的均值和互相关函数等统计特征，则可按统计矩的运算规律根据时域显式表达式直接求得响应的前两阶统计矩，这一方法称为时域显式直接法。若通过数值模拟手段生成大量随机激励样本，则可结合时域显式表达式进行高效蒙特卡罗模拟，这一方法称为时域显式蒙特卡罗模拟法。

为了解决随机列车荷载作用下冻土路基动力响应分析这一工程问题，本文首先提出一种随机列车荷载的简化模拟方法，以获取随机分析所需的荷载样本。然后，通过有限元脉冲响应分析构建路基结构动力响应的时域显式表达式。在此基础上，进一步利用时域显式蒙特卡罗模拟法，对随机列车荷载作用下冻土路基的关键响应开展统计分析，可大幅提高冻土路基结构随机振动的计算效率。最后，通过数值算例展示时域显式蒙特卡罗模拟法在冻土路基非平稳随机振动分析中的计算精度与效率。

1 随机列车荷载模拟方法

在冻土路基随机振动问题中，需要列车驶过引起的随机荷载的统计特性或大量样本作为输入。本文采用常见的二维路基模型［7］进行计算，此类模型需要列车行驶引起的随机轨枕竖向作用力作为荷载输入［15］。目前，相关实测数据较少，难以满足冻土路基随机振动分析的需求。为了获取分析所需输入，可以对确定性列车荷载的数值模拟方法［22-24］加以改进，在其中引入随机参数，进而生成大量随机列车荷载样本。

列车在轨道上行驶的简图如图1 所示，其中列车行驶速度为v。为了描述列车在沿轨道方向上的位置，建立如图1 所示的直线坐标系Ox。列车前端的初始坐标假定为-L′0。

图1 列车行驶简图Fig. 1 Moving train schematic

考虑如图1 所示的列车模型，其车厢的数量为N，包括机车和普通两类车厢。在列车行驶过程中，每个轮对的荷载通过轨道及轨枕传递到路基顶面。对于某一关注轨枕，列车对路基的竖向作用力F(t)的表达式为

式中：fi(t)表示第i节车厢的荷载传递到关注轨枕下方的部分，可进一步表示为该车厢所有轮对产生的竖向轨枕力之和。若该车厢为机车车厢，则其表达式为

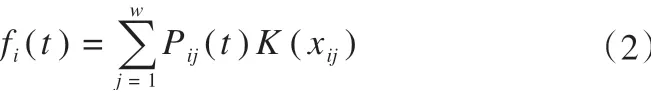
式中：w为车厢轮对数量，其中机车和普通两类车厢的轮对数分别为6 和4；Pij(t)为第i节车厢第j组轮对在轨道上产生的荷载；K(xij)为关注轨枕对轮对作用力的分担系数，按日本规范的经验假设轮对荷载. 附 近5 根. 枕 按0.1∶0.2∶0.4∶0.2∶0.1 分担［25］，可进一步表示为

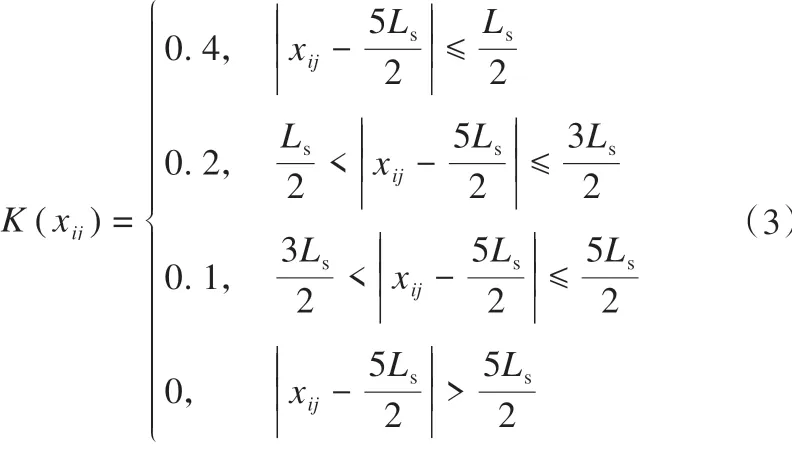
式中：Ls为轨枕间距，如图2 所示；xij为轮对在Ox坐标系中的坐标。当第i节车厢为机车车厢时，xij具体表示为

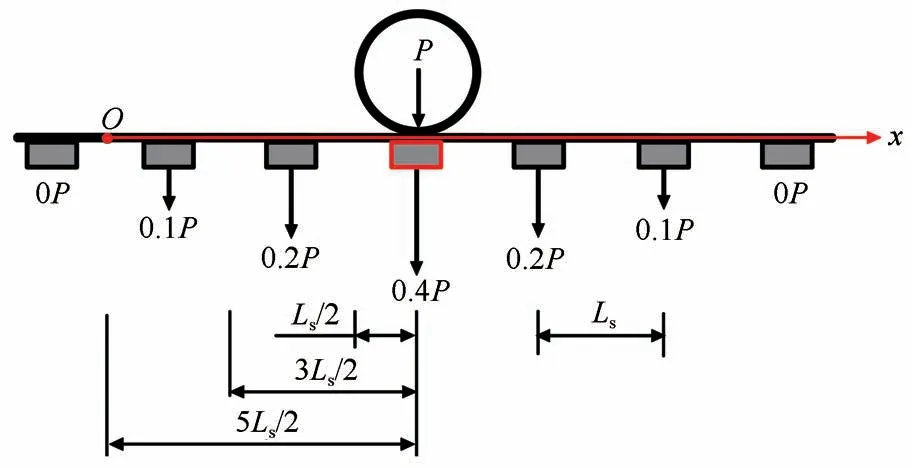
图2 道床顶面荷载沿线路方向分布图Fig. 2 Distribution of loading on top surface of road bed along the road

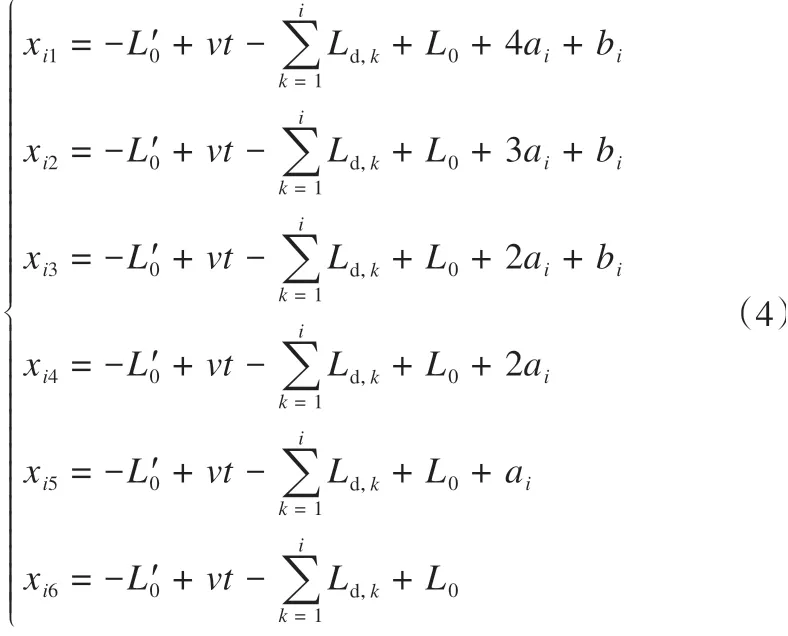
式中：ai第i节车厢同一个转向架内相邻两个轮对的轴距；bi为第i节车厢不同转向架相邻两个轮对的轴距；Ld，k为第k节车厢长度；L0为车厢后端与该车厢最后一组轮对水平方向上的距离；-L′0为列车前端在该坐标系内的初始坐标。当第i节车厢为普通车厢时，也可以参考图1 采用类似的方式计算轮对坐标。

列车第i节车厢第j组轮对产生的作用力Pij(t)可以采用反映行车平稳性、附加动载和轨面波形磨耗效应三个控制条件的激励力来模拟［24］，其表达式为

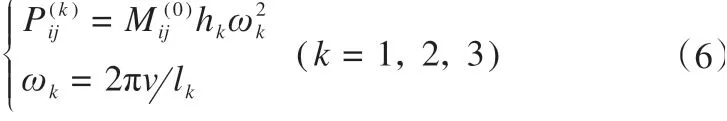
轨道几何不平顺曲线波长及相应的正矢和列车行驶速度都具有一定的不确定性［14］。可以引入相应的随机变量，以量化这些参数的不确定性。对描述相关参数的随机变量进行抽样，将样本代入式（5）计算轮对在轨道上产生的作用力，进而根据式（1）可以计算所关注轨枕的竖向作用力，即可获得后续分析所需的随机列车荷载样本。

2 冻土路基随机振动分析的时域显式蒙特卡罗模拟法

作为一种多孔结构的物质，冻土中包含了土、水、冰、气四种成分，其动态力学行为较为复杂。为了实现对冻土路基这一复杂工程结构的随机振动分析，需要在反映冻土动力响应本质特征的前提下，对问题进行简化以降低建模难度和提升分析计算效率。冻土力学性质对季节性温度变化十分敏感，然而本文关注的列车荷载作用下冻土路基动力响应分析问题最多仅考虑数分钟的时程，因此可将列车荷载作用期间冻土温度及力学性质视为不变［26-27］。此外，列车荷载引起的冻土应变相对较小，特别是在冻结状态下，一般不会造成路基下方冻土的塑性变形［28］。因此，为降低后续非平稳随机振动分析的难度，可将冻土路基中各土层假定为各向同性线弹性材料［29-30］。

2.1 动力响应显式表达式

根据上述假定，可将列车荷载作用下冻土路基的动力响应分析问题简化为线性非平稳随机振动问题。时域显式蒙特卡罗模拟法是解决这类问题的高效手段。在该方法中，首先需要建立结构响应的时域显式表达式。将冻土路基离散为具有nd个自由度的有限元模型，在非平稳随机激励作用下该结构的运动微分方程可表示为

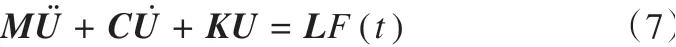
式中：M，C，K分别表示冻土路基结构的质量矩阵、阻尼矩阵和刚度矩阵；U，U̇，Ü分别为位移、速度和加速度向量；L为定位随机激励的nd× 1 阶常向量；F(t)为具有非平稳性的随机列车荷载。

将时间步长记为Δt，时程积分步数记为n，并把列车荷载F(t)离散为各时刻t1，t2，…，tn处的荷载F1，F2，…，Fn，定义状态向量为V=[UTU̇T]T。采用任意一种数值积分方法求解式（7），均可得到路基结构动力响应关于各时刻列车荷载的显式表达式。不失一般性，可假设结构初始状态V0=V(0) = 0以及荷载F0=F(0) = 0，则ti=iΔt时刻结构的状态向量Vi=V(ti)的显式表达式为

式中：Ai，1，Ai，2，…，Ai，i为只与路基结构参数有关的系数向量，反映结构参数对结构动力响应的影响。

参考文献［18］和［31］推导了系数向量的闭合公式，如下式所示：

式中：T，Q1和Q2的表达式由求解式（7）时所采用的积分格式决定，当采用Newmark-β积分格式［31］，可进一步表示为

式中：γ= 0.5，β= 0.25 为Newmark-β算法中的计算参数。

式（9）展示了各系数向量间的内在联系。根据该关系，可将各时刻结构响应显式表达式所需的系数向量排列成如表1 所示。由表1 可以看出，仅需计算第一列系数向量Ai，1(i= 1，2，…，n)即可获得所有时刻响应的显式表达式，其计算量与1 次确定性时程分析的计算量相当。该列系数向量的物理含义如图3 所示，可方便地通过在结构上施加单位三角脉冲激励进行时程分析求得。在存储量方面，由于结构随机响应分析中并不需要关注结构的全部响应，因此Ai，1(i= 1，2，…，n)中的元素不需要全部储存。假设所关心的结构响应量个数为m，则需要存储的元素个数仅为2mn，其中n为时程分析步数。可见，需储存的系数向量元素个数与结构自由度数无关，即使对于大型复杂路基结构随机振动问题，在矩阵元素的存储方面也不会出现问题。从本质上看，这是由于结构的物理演变机制已经在式（8）中得到全面反映，结构响应已经全部解耦，可以仅对所关心的响应量进行后续随机分析而不涉及其他响应量，这是采用时域显式表达式的主要优势之一。

表1 各时刻结构响应对应的系数向量Table 1 Coefficient vectors for structural responses at each time instant

图3 在时刻t1施加全三角单位脉冲激励Fig. 3 Unit impulse excitation at time t1

2.2 关键响应均值、标准差和平均峰值的计算

在工程结构分析中，通常只关注少量的结构关键响应。对于结构某一关键响应r，由式（8）可以得到关于r的一维显式表达式为

其中

式中：q为由状态向量V转换得到关键响应r的转换行向量，当r为某一位移或速度响应时，q由元素0和1 组成；当r为某一应力响应时，q依赖于相应的本构关系。

通过本文第1节所述方法生成大量随机列车荷载样本，假设一共得到M个列车荷载F(t)的样本。在第k个向量样本Fk(t)(k= 1，2，…，M)作用下，由式（11）可以得到关键响应r在各时刻的值为

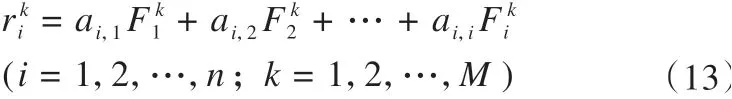
则关键响应r的均值、标准差和平均峰值分别为

可见，利用所建立的时域显式表达式，结合蒙特卡罗模拟，可以高效地计算关键响应的统计值，这种方法称为时域显式蒙特卡罗模拟法。而在传统蒙特卡罗模拟法中，对于每一个列车荷载样本，均需要根据时程分析法求解式（7）所示的运动微分方程。因此，时域显式蒙特卡罗模拟法的计算量远小于传统蒙特卡罗模拟法的计算量，从而可以使蒙特卡罗模拟法直接应用于冻土路基的随机振动分析。

3 数值算例

3.1 随机列车荷载

本文主要考虑轨道几何不平顺曲线波长、相应的正矢以及列车行驶速度的不确定性。引入服从高斯分布的随机变量［24，32-33］，以量化轨道不平顺波长、正矢和列车行驶速度的不确定性，如表2 所示。列车荷载模拟过程中采用的时间步长为Δt=0.005 s，考虑列车编组的方式为2 节NJ2 机车+4 节YZ25T 客车，即式（1）中N= 6，列车模型参数如表3所示。图1 中列车前端的初始坐标可以假定为L′0=0，图2中轨枕间距为Ls= 0.556 m。对表2所列的随机变量进行抽样，将一组样本代入式（5）和式（6）中，就可以得到轮对在轨道上产生的作用力，然后根据式（1）和式（2）即可得到所关注轨枕的竖向作用力，获得一个荷载样本。

表2 波长、正矢和车速随机变量Table 2 Random variables of wavelength，versine and vehicle speed

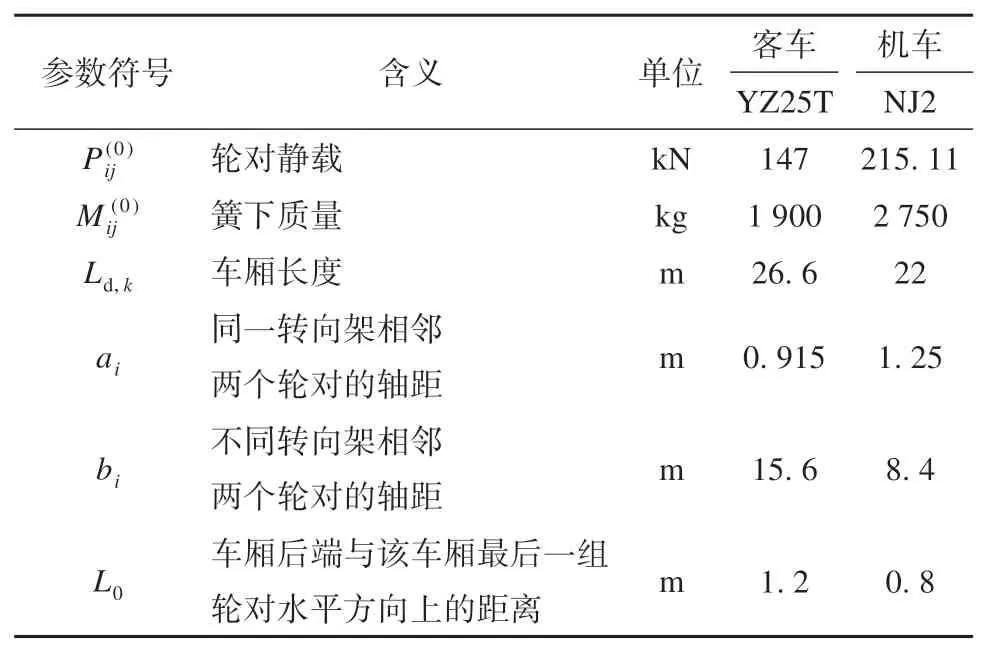
表3 青藏铁路列车模型参数［34］Table 3 Vehicle model parameters of Qinghai-Tibet Railway［34］

为验证本文提出的随机列车荷载模拟方法的准确性，将生成的一个荷载样本与文献［15］中采用车辆-轨道耦合动力学计算所得的轨枕竖向作用力时程进行对比，如图4 所示。由图4 可知，本文方法得到的荷载样本在幅值和波形上与文献［15］的方法得到的荷载时程结果吻合，说明本文所提的随机列车荷载模拟方法是可行的。

图4 列车荷载时程样本Fig. 4 Time history sample of train load

3.2 路基结构参数

以青藏铁路某传统道砟路基为研究对象，计算模型如图5所示。计算区域中的土层依次为道碴层、路基填土层、砂土层、粉质黏土层及弱风化岩层，如图5（a）所示。冻土的力学参数不仅依赖于各土层材料，还取决于土层的温度。本文选取青藏铁路路基修建完成后第10 年夏冬两个典型季节气温最高时路基内部的温度分布，根据参考文献［7］中的拟合公式计算路基各土层的力学参数，结果见表4～5。

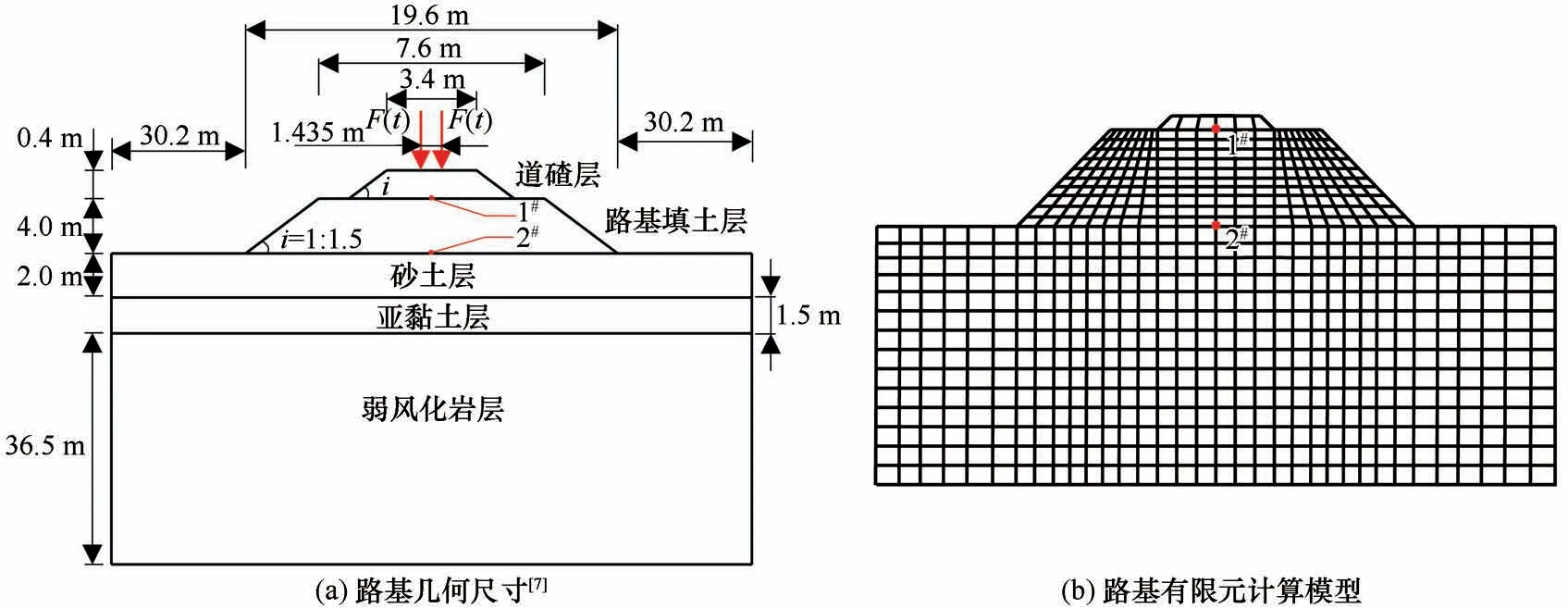
图5 二维冻土路基计算模型Fig. 5 Two-dimensional permafrost embankment model：geometry of embankment［7］（a），finite-element model of permafrost embankment（b）

表4 路基各土层的参考温度和力学参数（夏季）Table 4 Mechanical parameters of the soils in embankment model（Summer）

表5 路基各土层的参考温度和力学参数（冬季）Table 5 Mechanical parameters of the soils in embankment model（Winter）

根据表4～5 所得的各土层的力学参数，在通用有限元软件ANSYS 中建立二维冻土路基有限元计算模型。建模时按平面应变问题考虑［34-35］，采用PLANE42 单元，模型单元数为3 500，节点数为3 631，总自由度数为7 262，如图5（b）所示。考虑在路基两侧及底部布置黏弹性人工边界，在ANSYS中采用COMBIN14单元进行模拟，单元的刚度和阻尼参数根据文献［36］所述的方法确定。分析过程中选用瑞利阻尼［7］，阻尼参数为α=β= 0.03，时程积分步长取Δt= 0.005 s。在路基设计和监测过程中，路基填土层顶面和底面的竖向位移、竖向速度和竖向正应力是设计人员较为关注的关键响应，因此选择路基填土层顶面和底面的中点作为关注位置，分别记为1#点和2#点，如图5 所示。由于时域显式表达式独特的降维计算优势，在后续计算过程中可以只针对这两个关注位置进行降维计算，从而大幅度提升蒙特卡罗模拟的效率。

3.3 计算结果讨论

为验证所建立的时域显式表达式的计算精度，本文分别采用时域显式表达式和ANSYS 直接时程分析法计算冻土路基在一个列车荷载样本作用下的动力响应，结果如图6 所示。由图6 可知，采用两种计算方法得到的结果一致，从而验证了时域显式表达式在冻土路基动力响应分析中的计算精度。

图6 路基1#点竖向动力响应时程（夏季）Fig. 6 Time histories of dynamic responses at point 1#（Summer）：time history of vertical displacement（a），time history of vertical velocity（b），time history of vertical normal stress（c）

为展示时域显式蒙特卡罗模拟法相比于传统蒙特卡罗模拟法的效率优势，分别采用了不同数量的样本作为输入进行随机分析，两种方法所需计算时间如表6 所示。由第2.1 节中的分析可知，时域显式蒙特卡罗模拟法的计算时间包括求取系数向量的计算时间和实施蒙特卡罗模拟的计算时间两部分。由于该方法在实施蒙特卡罗模拟时无需反复求解冻土路基结构运动微分方程，第二部分耗时很短。而传统蒙特卡罗模拟法在每次样本分析中均需求解路基结构运动微分方程，计算非常耗时，其效率远低于时域显式蒙特卡罗模拟法的计算效率。由表6还可以看出，随着样本数的增大，传统蒙特卡罗模拟法计算时间呈线性增长，而时域显式蒙特卡罗模拟法的计算时间增长不多，说明当样本数量规模较大时，时域显式蒙特卡罗模拟法的计算优势更加明显。

表6 两种不同方法的计算时间比较Table 6 Comparison of time costs between two methods

当随机激励样本数分别取500、1 000 和2 000时采用时域显式蒙特卡罗模拟法获得的夏季冻土路基竖向位移、竖向速度和竖向正应力计算结果同时显示于图7 中。由图7 可以发现，当样本量达到1 000时，冻土路基各随机响应的均值和标准差结果已经收敛。由表6 可知，采用传统蒙特卡罗模拟法处理1 000 个样本耗时约4 d，而时域显式蒙特卡罗模拟法耗时约6 min。

图7 不同样本数下路基1#点2#点竖向动力响应统计矩时程（夏季）Fig. 7 Statistical moment time histories of dynamic responses at point 1#and point 2#with different numbers of samples（Summer）：mean value time histories of vertical displacements at point 1#and point 2#（a），mean value time histories of vertical velocities at point 1#and point 2#（b），mean value time histories of vertical normal stresses at point 1#and point 2#（c），stadnard deviation time histories of vertical displacements at point 1#and point 2#（d），standard deviation time histories of vertical velocities at point 1#and point 2#（e），standard deviation time histories of vertical normal stresses at point 1#and point 2#（f）

由时域显式蒙特卡罗模拟法还可以得到夏季和冬季冻土路基1#点和2#点动力响应平均峰值，结果如表7 所示。由表7 可知，列车荷载作用下冻土路基的动力响应不仅与路基深度有关，还受季节变化影响。总的来说，夏季时路基浅层的位移和速度响应最为剧烈，这是因为冻土是一种对温度敏感的土体。夏季温度相对冬季较高，导致冻土的弹性模量等力学参数降低，从而导致了路基中更为剧烈的位移和速度响应。

表7 夏季和冬季冻土路基响应平均峰值Table 7 Mean peak value of permafrost embankment in Summer and Winter

4 结论

冻土路基随机振动问题十分复杂，目前对冻土路基随机振动的理论研究较少。本文对上述问题展开了探索性的分析与研究，取得了一定的研究成果。基于以上分析研究，得到的主要结论如下：

（1）采用本文提出的随机列车荷载模拟方法，可以快速生成冻土路基随机振动分析所需的大量列车荷载样本用于蒙特卡罗模拟。

（2）本文采用时域显式蒙特卡罗模拟法计算了冻土路基在两个典型季节下的动力响应平均峰值，发现路基的位移和速度响应在夏季最为剧烈。

（3）对比了时域显式蒙特卡罗模拟法和传统蒙特卡罗模拟法在处理不同数量的样本时所需的计算时间，展示了时域显式蒙特卡罗模拟法在处理冻土路基随机振动问题中的计算精度和效率。

（4）本文中的时域显式表达式仅适用于线性系统，因此将冻土理想化为线弹性材料，这一理想化带来的误差尚需进一步分析。

由于目前尚无随机列车荷载的现场实测数据，因此本文仅从计算理论上进行初步探索，以期能为冻土路基的设计、维护及研究提供理论依据和参考。冻土是一种多孔多相材料，特别是在夏季高温时其力学行为十分复杂。为反映这一特性，后续研究将结合等效线性化方法，考虑非线性冻土本构关系，计算冻土路基永久变形和可靠度。