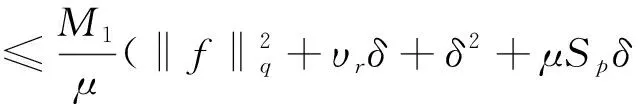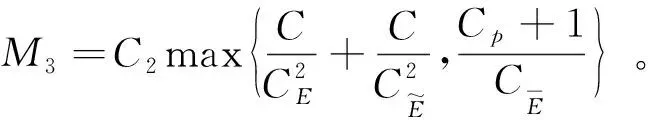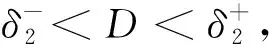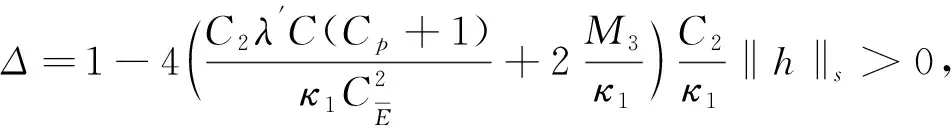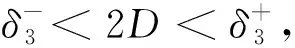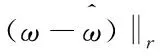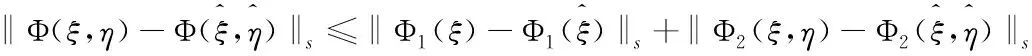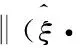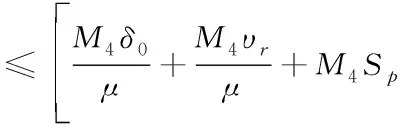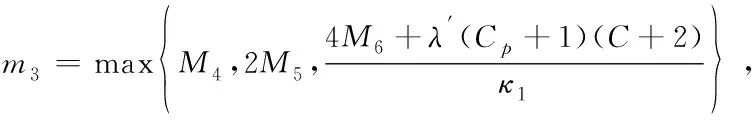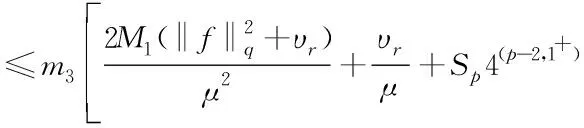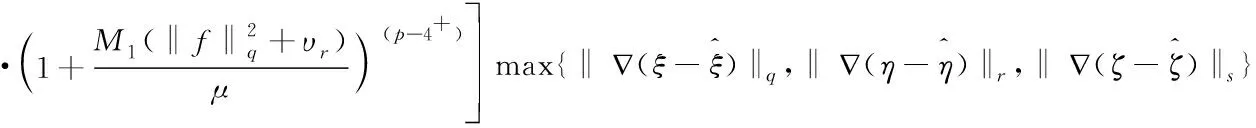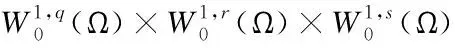一类具有热对流作用的非牛顿微极流体方程组的强解

段雨希， 王长佳

(长春理工大学 数学与统计学院， 长春 130022)

0 引 言

在三维空间中考虑如下具有热对流作用的非牛顿微极流体方程组的Dirichlet边值问题

(1)

式中：ui,j=∂jui(x),ωi,j=∂jωi(x)。

微极流体模型是Eringen在文献[1]中首次提出的，它考虑了流体颗粒的微观结构，是关于流体动力学中的经典模型 Navier-Stokes方程的根本推广，在理论和应用上都涵盖了比经典模型更多的现象。当p=2时，问题(1)成为经典的牛顿流模型，目前已有大量的研究成果可参见文献[2-7]。当p≠2时，问题(1)成为非牛顿流模型，此时方程组所具有的退化性或奇异性会为这类问题研究带来本质困难，相关研究结果还不多。在不考虑热对流作用(即θ=0)时，Araújo等在文献[8]中通过结合使用Galerkin方法与紧性方法证明了其弱解的存在性，并讨论了解的唯一性与周期性结果；文献[9]在二维光滑有界区域上讨论了其解的渐近性，并证明了系统拉回吸引子的存在性以及关于黏性系数的上半连续性，有关微极流体模型的更多结果见文献[10-20]。本文研究具有热对流作用(即θ≠0)的非牛顿流问题(1)，应用不动点定理，在外力项和涡旋粘性系数适当小的条件下，证明了该问题强解是存在且唯一的。

1 预备知识

首先介绍本文所能用到的基本知识。

引入空间

对于x,y∈，记(x,y)+=max{x,y}，x+=max{x,0}，Sp=(|p-2|,2)+。

引入常数

且本文中用Cp表示Poincaré常数。

对于q>r>s>3和δ>0，用Bδ表示由下式定义的凸集：

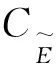
‖(ξ,η,ζ)‖1,q,r,s:=max{‖∇ξ‖1,q,‖∇η‖1,r,‖∇ζ‖1,s}

本文用到的引理如下。

引理1[21]令m≥-1为整数，Ω为n(n=2,3)中的有界域，边界∂Ω∈Ck，k=(m+2,2)+。则对于任意τ∈Wm,ρ(Ω)，问题

存在唯一解(u,p)∈Wm+2,ρ(Ω)×Wm+1,ρ(Ω)，并且以下估计式成立。

‖∇u‖m+1,ρ+‖p‖m+1,ρ/R≤Cm‖τ‖m,ρ

式中Cm=Cm(n,ρ,Ω)为正常数。

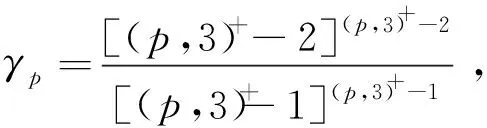
AD+ED2rp(1+D)(p-4)+≤γp

成立，则F至少有一个根δ0，且δ0>D。此外，对每个β∈[1,2]，下列估计式成立：

‖T(u)-T(v)‖Y≤K‖u-v‖Y,∀u,v∈B, 0

则T在B上存在唯一不动点。

2 主要结果及证明

本文的主要结果如下：

(2)

成立，则问题(1)存在唯一强解

对上述结论，本文将通过以下四步进行证明。

第一步： 问题的线性化及映射的构造。

首先，将问题(1)重新表述如下：

(3)

根据引理1、椭圆型方程理论以及文献[2]可知，问题(3)存在解

为此可定义映射

T:(ξ,η,ζ)→(u,ω,θ)

第二步： 证明映射T为Bδ0到它自身的映射。

这部分本文将证明存在常数δ0>0，使得T为Bδ0到Bδ0的映射，主要结论如下。

命题1设q>r>s>3，p>1，μ>0，f∈Lq(Ω)，g∈Lr(Ω)，h∈Ls(Ω)，存在正常数

(4)

成立，那么存在δ0>0，使得T(Bδ0)⊆Bδ0。

证明设(ξ,η,ζ)∈Bδ。根据引理1知，u∈V2,q，且满足

(5)

下面估计式(5)右端各项，首先有

(6)

(7)

其次，由文献[22]中的推导有

(8)

结合式(5)～式(8)，得到

另一方面，利用椭圆型方程估计理论可知，存在正常数C1，使

‖∇ω‖1，r≤C1[‖ζg‖r+‖2υrrotξ‖r+‖4υrη‖r+‖ξ·∇η‖r]

≤C1[‖ζ‖∞‖g‖r+2υrC‖∇ξ‖r+4υrCp‖∇η‖r+‖ξ‖∞‖∇η‖r]

≤C1[δ(Cp+1)‖g‖r+Cυr‖∇ξ‖1,q+4υrCp‖∇η‖1,r+CE(Cp+1)‖∇ξ‖q‖∇η‖1,r]

然后，由方程(3)及椭圆方程估计知，存在正常数C2，使得

(9)

式中

所以有

(10)

又因

‖κ′(·,ζ)|∇ζ|2‖s=‖(κ′(·,ζ)-κ′(·,0))|∇ζ|2‖s

(11)

‖ξ·∇ζ‖s≤‖ξ‖∞‖∇ζ‖s≤CE‖ξ‖1,q‖∇ζ‖s≤(Cp+1)CE‖∇ξ‖q‖∇ζ‖s

(12)

结合式(9)～式(12)，可得

不妨假设δ≤1，因此，为了确保T(Bδ)⊆Bδ，则仅需以下条件成立：

(13)

在引理2中取β=2，得

其次，可将不等式(13)中的第二个不等式重新写为

(14)

此时，存在δ使得式(14)成立。

最后，可将不等式(13)中的第三个不等式重新写为

(15)

此时，存在δ使得式(15)成立。

综上可得

因此，取δ0=δ1，有T(Bδ0)⊆Bδ0。

第三步：证明T:Bδ0→Bδ0为压缩映射。

(16)

式中

首先，根据引理1可得

(17)

下面估计式(17)的右端各项。首先根据文献[22]中推导有

(18)

(19)

其次有

(20)

(21)

结合式(17)～式(21)，得到

(22)

另一方面，由椭圆型方程估计可知，存在正常数C3，使得

(23)

估计式(23)中的右端各项，有

(24)

(25)

(26)

(27)

结合式(23)～式(27)，得到

(28)

然后，由文献[2]可知，存在正常数C4，使得

(29)

式中

所以有

(30)

(31)

结合式(30)～式(31),可得

(32)

结合式(29)和式(32)有

(33)

结合式(22)、式(28)和式(33)有

(34)

第四步：定理1的证明。