基于CEEMDAN-PSO-Elman的电采暖短期负荷预测

陈中慧，王海云，常喜强，徐 森

(1. 新疆大学电气工程学院，新疆 乌鲁木齐 830047；2. 国网新疆电力有限公司，新疆 乌鲁木齐 830011)

1 引言

为解决新疆地区燃煤供暖带来的雾霾等环境污染问题，促进新能源消纳能力缓解弃风弃光情况，新疆人民政府于2016年7月5日印发《关于扩大新能源消纳促进能源持续健康发展的实施意见》提出加快推进电锅炉、电供暖等基础设施的建设，逐步替代传统燃料供暖方式。随着煤改电工程的推进，冬季电采暖负荷的加大给电能质量以及电网安全稳定运行带来挑战[1]。精确的电采暖负荷预测不仅保证电网安全稳定运行还可以对电力系统进行调峰、调频[2]。

目前，短期负荷预测主要有统计学方法与机器学习方法两大类[3]。常用的统计学方法有线性回归法与时间序列法[4]，其中多元线性回归是线性回归分析法中经典的预测方法[5]，但该方法对样本数量大具有随机波动性的时间序列预测精度不高。机器学习法主要有支持向量机(support vector machine，SVM) 、人工神经网络法(artificial neural netwoks，ANN)等，其中人工神经网络可以很好学习序列的非线性特征[6]。文献[7]采用经验模态分解(Ensemble Empirical Mode，EMD)将负荷数据分解为有限个子序列，然后采用经过层标准化(LN)优化处理的长短期记忆网络进行短期负荷预测。其中EMD分解虽然降低了负荷数据的随机波动性，但存在严重的模态混叠问题，影响负荷预测精度。文献[8]采用集成经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)将历史电采暖负荷数据分解为一系列子序列，针对不同子序列分别建立BP神经网络预测模型，最后汇总各预测模型的预测结果，得到最终的预测电采暖负荷。虽然EEMD一定程度缓解了EMD的模态混叠问题，但EEMD分的本征模态分量(Intrinsic Mode Function，IMF)含有残余噪声。且BP神经网络存在易陷入局部极小，收敛速度慢等问题。文献[9]针对电采暖负荷的随机波动性，通过充分挖掘电采暖负荷特点包括负荷最大值、最小值、负荷各时刻变化趋势、负荷各时刻波动特征、负荷大幅度突变特征等，形成历史数据特征集。然后将历史数据特征集作为训练样本应用核极限学习机(kernel extreme learning machine，KELM)模型进行电采暖短期负荷预测。该方法有效降低了电采暖负荷随机波动性对预测精度的影响。但并未考虑气象数据对电采暖负荷的影响。文献[8]与文献[9]的BP神经网络预测模型与KELM预测模型不具记忆性，对历史数据不敏感，不能充分挖掘电采暖负荷的时间关联性。文献[10]首先确定长短期记忆网络(long short-term memory，LSTM)的模型参数，然后采用分析得出的不同采样间隔下的最优训练步长分别建立LSTM神经网络预测模型均取得了较好的预测效果。虽然LSTM充分挖掘了电采暖负荷序列的时间相关性但是LSTM网络结构复杂，涉及大量预测数据计算量大、训练速度慢还会存在梯度消失的问题。

针对上述问题，文章提出了基于CEEMDAN-PSO-Elman神经网络的电采暖短期负荷预测方法。采用CEEMDAN将电采暖负荷数据分解为有限个IMF分量和一个剩余分量。CEEMDAN不仅解决了EMD存在的模态混叠问题，还克服了EEMD由于添加不同幅值白噪声造成IMF分量中噪声残留的问题。应用Elman神经网络对不同分量建立预测模型，Elman神经网络与BP神经网络、KELM等预测模型相比具有记忆性对历史数据敏感可以充分挖掘电采暖负荷序列的时间相关性，且与LSTM模型相比结构简单，计算量小。对CEEMDAN分解的分量分别建立PSO-Elman模型，叠加各预测模型结果，经过算理仿真分析验证了所述方法有效提高了电采暖负荷预测精度。

2 自适应噪声完备经验经验模态分解

CEEMDAN是在EEMD分解的基础上改进的[11]。CEEMDAN分解方法通过对每次加入自适应噪声的分量进行EMD分解，然后平均分解结果得出唯一本征模态分量IMF，很大程度上缓解了EMD模态混叠问题和EEMD分解中IMF噪声残留问题。CEEMDAN适用于非线性、非平稳信号。CEEMDAN分解的具体步骤如下[12]。

文章定义求解IMF分量时的自适应系数为εi-1，第i次加入的零均值单位方差白噪声用wi(n)表示，以及EMD及CEEMDAN分解算法得到的第k 个IMF分量分别为Ek(·)、fIMFk。

1)在原始信号x(n)中加入噪声分量ε0wi(n)进行EMD，并在第i次加入白噪声后分解出第一个IMF分量

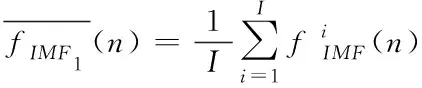
(1)

式中I为加入白噪声次数。

2)1计算CEEMDAN的第一个余量信号

(2)

3)向式(2)的剩余信号中加入自适应白噪声ɛ1E1(wi(n))后，对其进行EMD分解，求解第二个IMF分量

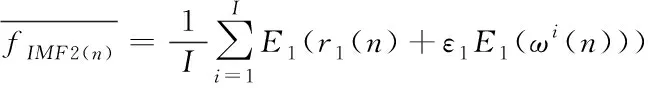
(3)

4)重复步骤2)、3)，可得到第k个余量信号和k+1阶IMF分量分别如式(4)和式(5)所示

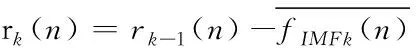
(4)

(5)

5)重复步骤4)，直至余量信号无法进行EMD分解时终止。

假设算法终止后分解出K个IMF分量，则最终的余量信号为

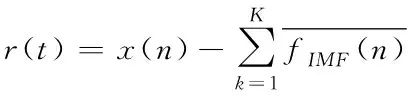
(6)

3 基于PSO优化的Elman神经网络

3.1 Elman神经网络

Elman神经网络是由J.L.Elman提出的一种典型动态递归神经网络[13]。Elman神经网络是在BP神经网络的基础上增加了承接层作为一步延时算子[14]，使得Elman神经网络具有记忆能力，对历史数据敏感，提高了对动态信息的处理能力，解决了BP神经网络不具备动态特性的问题。Elman神经网络结构如图1所示。

图1 Elman神经网络结构图

由图1可以看出Elman神经网络由输入层、隐含层、承接层、输出层组成的。其中输入层仅仅具有信号传输信号的作用，输出层具有输出信号加权的作用。隐含层的激励函数采用Signmoid非线性函数，承接层具有记忆隐含层前一时刻的输出信号的作用，是一个有一步延迟的延时算子。承接层将前一时刻隐含层的输出信号反馈给当前时刻隐含层输入，这种连接方式使得Elman神经网络对历史数据敏感，使网络具有处理动态信息的能力，即达到了动态建模的目的[15]。

Elman神经网络的数学表达是如下

y(t)=g(w3x(t))

(7)

x(t)=f(w1xc(t)+w2(u(t-1)))

(8)

xc(t)=x(t-1)

(9)

式中u为r维输入向量；y为m维输出向量；x为n维隐含层向量；xc为n维反馈状态向量；w1、w2、w3分别为隐含层到承接层连接权值、输入层到隐含层连接权值、隐含层到输出层连接权值。f(·)为隐含层的传递函数；g(·)为输出神经元的传递函数。

3.2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是根据鸟类捕食行为研发的一种群体智能优化算法。算法中每个粒子代表优化问题的一个潜在解。每个粒子根据适应度函数(Fitness)计算得到适应度值，适应度值决定粒子的优劣[16]。适应度函数(Fitness)公式如下

(10)

式中N为样本总数目；m为粒子维数；pij与tij分别为第i个样本的第j维数据的重构值与实际值。

粒子的速度决定了粒子的移动方向与距离。个体极值(Pbest)是指个体所经历位置中对应适应度值最优的位置，群体极值(Gbest)是指种群中搜索到的所有粒子对应适应度值最优的位置[17]。在进行每一次迭代时，粒子跟踪Pbest和Gbest更新个体位置，通过多次迭代得到问题的全局最优解[18]。

假设在D维搜索空间，M个粒子构成种群X=(X1，X2，…，XM)，其中第j个粒子在解空间的位置可表示为Xj=(xj1，xj2，…，xjD)T，第j个粒子的速度可表示为Vj=(vj1，vj2，…，vjD)，第j个粒子个体极值可记为Pbest=(pj1，pj2，…，pjD)，第j个群体极值记为Gbest=(gj1，gj2，…，pjD)，在迭代过程中粒子的速度和位置更新公式如下所示

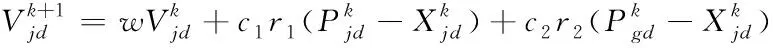
(11)

(12)

式中k为当前迭代次数；w为惯性权重，c1与c2为加速因子，r1与r2为在(0，1)范围内的随机数。d=1，2，…，D；j=1，2，…M。

3.3 PSO-Elman神经网络模型

采用具有快速全局寻优能力的PSO优化算法优化Elman神经网络的权值和阈值解决其易陷入局部极小值、收敛速度慢等问题，提高Elman模型的预测精度。PSO优化Elman神经网络参数具体步骤如下：

1)由输入输出样本数据确定Elman神经网络结构，根据神经网络的所有连接权值与阈值来确定粒子的维度。

2)粒子群种群初始化，即初始化粒子群参数包括迭代次数，惯性权重w，加速因子c1与c2。把Elman神经网络的连接权值与阈值映射到粒子的各维度。

3)利用式(10)计算各粒子的适应度值，在当前粒子适应度与个体极值Pbest适应度中选择适应度值较大的更新体极值Pbest，同理更新群体极值Gbest。

4)运用式(11)、(12)更新各粒子的速度和位置。

5)当达到最大迭代次数或者群体极值Gbest达到设定值，终止寻优。否则返回步骤3)。

4 CEEMDAN-PSO-Elman预测模型的建立

4.1 电采暖负荷影响因素的分析

电采暖负荷的影响因素有气象因素：温度、湿度等，日期类型：节假日、周几、电价等。文章首先采用皮尔逊相关系数对该地区的电采暖负荷影响因素做相关性分析，然后采用相关性强的电采暖负荷影响因素作为CEEMDAN-PSO-Elman神经网络预测模型的输入。皮尔逊相关系数公式如下所示。

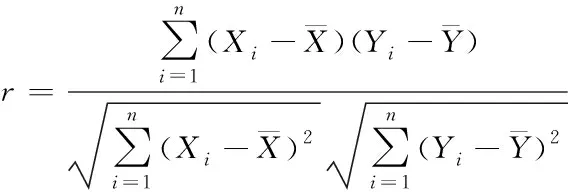
(13)

式中n为样本数量，Xi，Yi分别为样本量。

4.2 CEEMDAN-PSO-Elman模型流程

电采暖负荷的随机性、波动性影响负荷的预测精度，采用CEEMDAN将电采暖负荷序列分解为若干个较平稳更具规律性的子序列以期提高预测精度；对于电采暖负荷序列的时间相关特性采用对历史数据敏感的具有一定记忆性的Elman神经网络预测模型来充分挖掘电采暖负荷序列的时间关联性。此外应用PSO优化Elman神经网络参数克服Elman神经网络易陷入极小值问题，寻找全局最优解。文章建立基于CEEMDAN-PSO-Elman神经网络的电采暖短期负荷预测模型，流程图如图2所示。

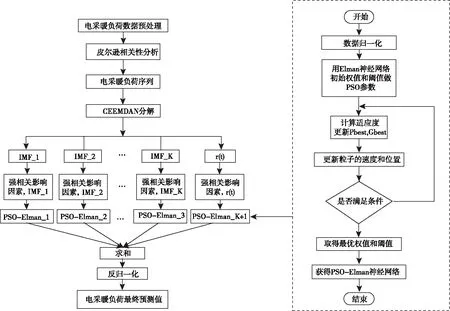
图2 基于CEEMDAN-PSO-Elman的电采暖负荷流程图具体步骤为如下。

1)对电采暖负荷数据进行预处理，填补空缺值，剔除异常值。

2)采用皮尔逊相关系数对电采暖负荷与电采暖影响因素做相关性分析，提取相关性强的影响因素与电采暖有功负荷数据作为负荷预测模型的输入。

3)将历史电采暖有功负荷序列进行CEEMDAN分解，得到有限个IMF分量和一个剩余分量。

4)对每个IMF分量、强相关电采暖影响因素与剩余分量、强相关电采暖影响因素分别建立PSO-Elman神经网络预测模型。

5)叠加不同分量的预测结果得到电采暖短期负荷预测的最终结果。

5 仿真分析

文章采用新疆某地区2019年1月1日至2019年12月31日期间110天的电采暖有功负荷数据、气象数据、日期类型进行仿真测试，数据的采样间隔为15min。

5.1 数据预处理与样本选取

由于电采暖负荷数据采集过程采样设备异常或通信设备故障等情况会造成采样数据缺失、异常等质量问题。首先剔除异常值，其次对缺失数据采用前一时刻与后一时刻值的一周的平均值进行填补。

采用皮尔逊相关系数对电采暖负荷与气温、相对湿度、节假日、周几、电价做相关性分析，共计10560*6个数据点。其中节假日用数字1表示，非节假日用数字0，周几用数字1-7表示，结果如表1所示。

表1 相关系数指标

皮尔逊相关系数的绝对值越接近1表明相关性越强。由表可知温度与电采暖负荷的相关性较强，因此选取温度作为电采暖负荷的影响因素与电采暖有功负荷作为预测模型的输入。选取前109天的的电采暖有功负荷数据与温度数据作为训练数据，每9天的电采暖有功负荷与温度数据作为输入向量，第10天的电采暖有功负荷数据作为目标向量，共得到100组训练样本。第100天的数据作为测试样本。

由于温度与电采暖有功负荷的量纲不同，为避免加大预测误差对数据进行归一化处理，将数据归一化到[0，1]之间，公式如下所示

(14)

式中x～表示归一化的数据；xmin表示样本数据中的最小值，xmax表示样本数据中的最大值。

5.2 预测结果分析

CEEMDAN将电采暖有功负荷序列分解为13个IMF分量和1个剩余分量r(t)结果如图3所示。

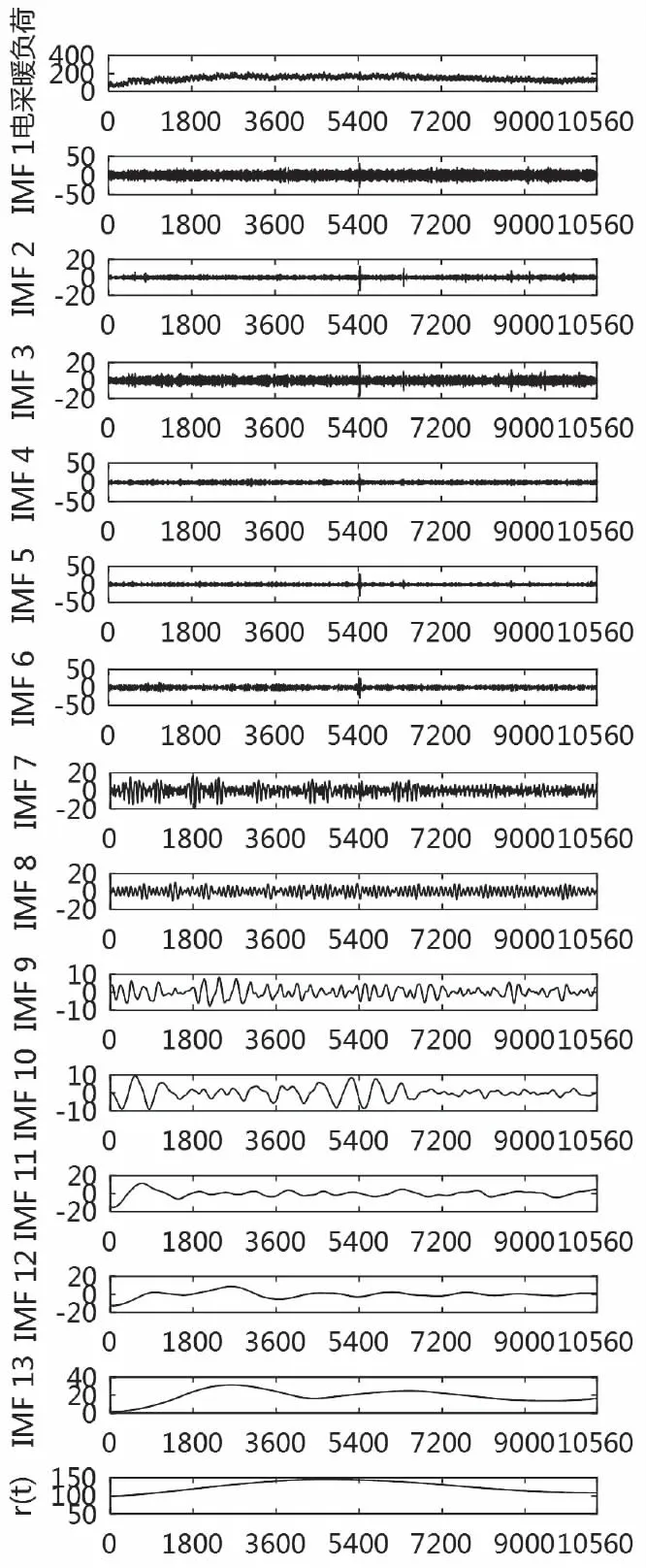
图3 CEEMDAN分解图

对以上14个电采暖有功负荷子序列与温度数据为输入分别建立PSO-Elman神经网络预测模型。为了验证文章预测模型的有效性将文章预测模型的预测结果与Elman神经网络模型与EEMD-BP神经网络模型的预测结果对比，如图4，图5所示。

图4 不同模型预测结果

图5 不同模型预测结果局部图

由图4和部分局部图5可以看出该文章预测模型具有较好的预测趋势，Elman模型与EEMD-BP预测模型在电采暖负荷尖峰与低谷处有较大误差。

为定量的分析不同预测模型的精确度，文章引用了MAE(平均绝对误差)进行误差分析、MAPE(平均绝对百分比误差)、RMSE(均方根误差)，其计算公式如式(15)-(17)所示。结果见表2。

(15)

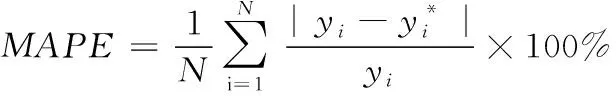
(16)

(17)

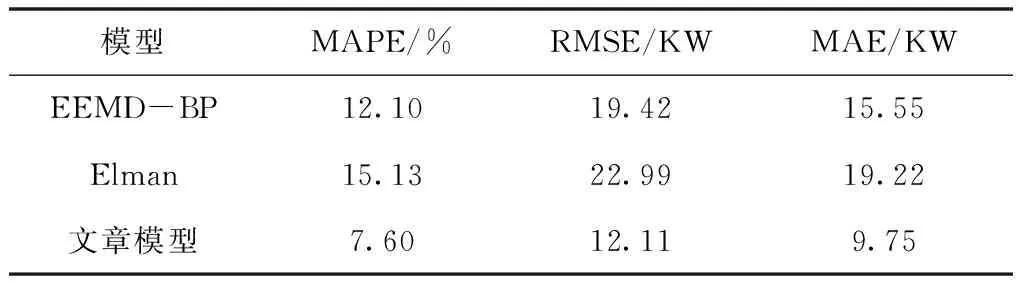
表2 各预测模型的误差评价指标

由表2可知，文章模型的平均绝对百分比误差比Elman模型降低了7.53%，比EEMD-BP模型降低了4.5%；文章模型的其它两种误差指标均小于Elman模型与EEMD-BP模型。证明了电采暖负荷的随机性波动性影响负荷预测精度。采用CEEMDAN分解电采暖负荷能够提高电采暖负荷预测精度，利用PSO优化模型参数，使得Elman避免陷入局部最优。

6 结论

文章提出基于CEEMDAN-PSO-Elman神经网络电采暖负荷预测模型，结合算例仿真分析得到如下结论。

1)采用CEEMDAN分解电采暖负荷，降低了电采暖负荷的随机波动性，消除不同趋势之间的影响，并且解决了EEMD分解噪声残留的问题，提高了预测精度。

2)采用PSO优化Elman神经网络模型参数，克服了Elman神经网络易陷入局部最小值，收敛速度慢等缺点。

3)Elman神经新增承接层是对BP神经网络的改进，提高了网络对历史数据的敏感性，适用于处理时间序列的电采暖负荷。

4)通过算例仿真该文章模型与Elman和EEMD-BP预测模型相比，MAPE降低了7.53%和4.50%，RMSE降低了10.88kW和7.31kW，MAE降低了9.47kW和5.80kW，表明该文章预测模型有效提高了电采暖负荷预测精度。