基于Copula函数模型的构成软件可靠性预测方法
房怀媛,李长银
(临沂大学,山东 临沂 273400)
1 引言
随着软件结构越来越复杂,错误率也大大增加。为了降低软件故障带来的损失,软件预测变得格外重要。因此,为了保证构件软件能够得到有效使用,需要对构件软件进行可靠性预测[1,2]。
目前,常用的软件可靠性预测方法主要有基于组合模型的、基于体系结构的和基于优化PSO-SVM模型的软件可靠性预测方法。其中,基于组合模型的软件可靠性预测方法为了提升软件测试精准度,建立一个组合模型。在模型故障数据类型、故障趋势匹配和模型预测的基础上阐述了模型选取算法。最后利用序列似然比方法对模型权值进行选取,再选择一组故障数据完成对组合模型的验证,该方法没有对软件缺陷进行有效分析,导致软件预测时间过高,存在时间延迟的问题。基于体系结构的软件可靠性预测方法为了解软件模块之间的调用关系对模块可靠度进行估算。根据不同的评估方法将模型划分为合成型与分级型两类,再通过可靠性评估对软件体系结构和模块划分原则进行分析,得出模块的可靠度和转移概率评估方法,为软件预测提供重要依据,该方法没有分析软件故障原因,导致构件软件在预测中系统能耗偏高,存在CPU开销大的问题。基于优化PSO-SVM模型的软件可靠性预测方法针对传统软件的预测模型弱点进行研究,更改传统PSO-SVM模型,并完善PSO-SVM软件预测模型,该方法获取的软件故障信息不全面,使程序输出具有误差,存在平均路径覆盖率差的问题[3,4]。
为了解决上述方法中存在的问题,提出基于Copula函数模型的构件软件可靠性预测方法。
2 构件软件故障模型可靠性预测
2.1 缺陷模型构建
在软件出现缺陷的过程中能够获取三个导致软件失效的主要原因:
1)程序的输入使软件缺陷得到了执行[5]。
2)缺陷改变后置数据,引发软件故障[6]。
3)出现错误信息的程序数据被散布到程序输出中,使输出结果出现偏差,软件失效。
这三个主要原因展现了软件从缺陷到失效的过程,程序存在缺陷后,陆续传递到数据中,经过无数次迭代,出现错误的数据就会将故障传播到程序的输出中。软件缺陷模型如图1所示。

图1 构件软件的缺陷模型
图1中,通过数据输入使位置数据得到执行的概率,表示为执行概率A;当数据位置出现改变时,数据状态遭到改变的概率被称作传播概率B;改变后的数据状态会产生程序输出变动,它的概率由传播概率C表示。当三个主要原因全部存在时,软件缺陷才会失效,也容易被检测出来。
当软件缺陷的发生概率D满足这三种原因时,它的概率乘积表示为D=A×B×C。
当系统出现故障时,就可以使用SFTA软件对失败事件进行分析,从中找寻发生故障的主要因素,通过分析因素的前后层次关系建立一个软件故障树,其故障分析如图2所示。

图2 SFTA事件说明
2.2 故障树顶事件
因为软件发生数据信息输入故障后,数据库不能及时进行数据更新,所以将顶事件放在故障树首位。居于故障树底端的被称作底事件,要想确立底事件分解级别就要确定SFTA的层次,如模块级、程序级或语句一级[7]。整个事件中,导致数据库不能及时更新数据的原因有如下几种假设条件:
1)更改程序遭到破坏;
2)用户不能正常登录;
3)用户登录后不能输入信息。
通过这几个假设条件对事件起因进行推导,追溯每一级事件故障的直接原因事件,此事件为确定底事件,如表1所示。

表1 软件故障分析
构造软件故障树是对软件故障分析的关键,按照国家标准GJB768.1,构建故障树的基本原则为:
1)确立故障树构建的边界条件;
2)严格定义故障事件;
3)自顶向底逐级建树;
4)建立故障树时逻辑门与逻辑门之间不能直接连接;
5)选取直接时间,消除间接时间;
6)对于多个时间同时发生的相同原因事件进行恰当处理。
根据表1的构件软件故障分析结果建立软件故障树,构建结果如图3所示。

图3 软件故障树流程图
由图3可知,M代表顶事件;N1代表软件更改程序遭到破坏;N2代表用户不能正常登录系统;N3代表用户不能填写信息或信息填写的错误;W1代表病毒入侵计算机;W2代表丢失加载文件;W3代表无法显示用户登录的界面;W4代表验证程序出现故障;W5代表用户实操出现错误;W6代表数据库内存不足;W7代表录入信息出现格式错误;Y代表其它事件;Y1代表硬件出现障碍;Y2代表系统模块发生障碍。
对于建立完成的故障树,可以从中获取构件软件产生故障的前后因果,为构件软件可靠性预测提供了更加全面的信息基础。
3 基于Copula函数的证据理论相关性模型
3.1 建立联合BPA
根据二维情况研究建立普通BPA证据变量,设M1和M2为两个证据变量,则与焦元dk相对应的边缘区间为[m11,m12]和[m21,m22],那么二维焦元如图4所示。
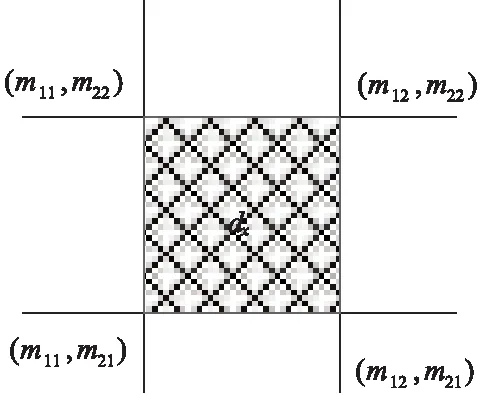
图4 二维焦元
图4中,边缘BPA分别由y1和y2表示,它的边缘区间端点用m11、m12、m21和m22描述,与边缘区间相对应的累积BPA分别为y11、y12、y21、y22。
在传统方法中,假设每个证据变量都是一个单独的个体,那么与dk相对应的联合BPA方程式如下所示

(1)
式(1)可被Copula函数修改为下述方程
y(dk)=C∏(y12,y22)-C∏(y11,y22)
-C∏(y12,y21)+C∏(y11,y21)
(2)
式中,C∏代表独立Copula函数。由此可见,Copula函数的特殊形式可以构建普通BPA,它被称作独立Copula[8]。因为证据变量中具有某些相关性情况,所以对于二维问题,将与焦元dk对应的联合BPA定义为
y(dk)=C(y12,y22|θ)-C(y11,y22|θ)
-C(y12,y21|θ)+C(y11,y21|θ)
(3)
式中,θ代表存在于Copula函数中的相关参数。在N维焦元中包括n个边缘区间[m11,m12],…,[mn1,mn2],则联合BPA由式(4)表示
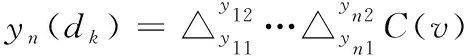
(4)
式中,v代表差分指数。式(4)还可以用下列方程表示
-C(v1,…,vj-1,yj1,vj+1,…,vn)
(5)
则与焦元dk相应的联合BPA定义如下
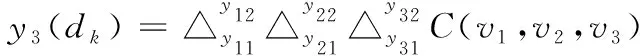
(6)
3.2 最优Copula函数
根据式(4)可知,当证据变量中存在相关性时,应当使用Copula函数差值获取联合BPA值,先对证据变量中的Copula函数进行辨识后,再对BPA进行计算。证据变量中所对应的大部分样本数量较少,所以采用贝叶斯方法有效避免样本量较小的问题,同时利用贝叶斯方法对Copula函数进行选择[9]。在证据理论中,使用经验分布公式对证据变量样本Mk(k=1,2,…,d)进行转换,转换成[0,1]中的均匀变量,其方程定义为

(7)
式中,d代表变量数目,Ri,k代表样本的秩(选择其中一个变量mk,从小到大排列,它的样本为m1,k,m2,k,…,mn,k,当样本数目小于等于mj,k时,被称作mj,k秩)。平等分布各个[0,1]的变量后,就可以采用贝叶斯方法获取证据变量中的最优Copula函数。
Copula函数有很多类型,目前为止使用最多的有Elliptical Copula函数和Archimedean Copula函数。其中Clayton、AMH、Gumbel、Frank、A12和A14属于Archimedean Copula函数,Gaussian Copula属于Elliptical Copula函数,Ind属于独立Copula函数。这些函数中,只有Gaussian Copula函数与经常使用的联合正态分布建立关系便利,建立后的方程式如下定义
CΦ(u1,u2,…,un|θ)=Φp(Φ-1(u1),Φ-1(un)|θ)
(8)
式中,ui=Φ(mi)代表标准的正态分布。
目前为止大部分Copula的运用只针对成对数据,因为部分Copula函数中具有多维模型,在实际操作时存在限制,给操作造成不便。假设在多维Archimedean Copula模型中存在相同的Copula函数和相关性参数,当变量不同时,模型中的Copula函数和相关性参数就会存在差异,模型就不能准确对变量间的相关性进行分析[10]。所以当多个变量出现变量相关性时,只对各个二元数据对应的相关情况进行考虑,再用独立Copula函数把各个二元Copula函数关联起来。
3.3 构件软件可靠性预测分析
对于以上证据理论模型的相关性研究,提出了对构件软件结构可靠性的分析方法。当矢量X中存在多维证据矢量时,它的不确定性结构可靠域R可用方程表示为
R{g:g(x1,…,xn)≥0}
(9)
式中,g代表功能函数,其多维识别框架定义如下
D=X1×…×Xn
={dk=[x1i1,…,xnin],x1i1∈X1,…,xnin∈Xn}
(10)
式中,通过[x1i1,…,xnin]对焦元dk进行构建,再利用式(4)对证据变量联合BPA进行计算。依据联合BPA与可靠域R计算出可信度Bel和似真度Pl,具体如下所示
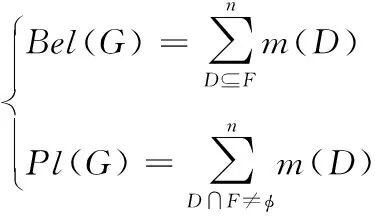
(11)
式中,Bel(G)表示完全支持G的证据BPA总和,Pl(G)表示全部或部分完全支持G的证据BPA总和。
理论上讲,PR=P{g(x1,…,xn)≥g0}为真实的结构可靠度,其归于区间Bel(G)≤PR≤Pl(G)中。
利用Bel和Pl对可靠度进行计算,当D⊆R时,焦元D全部居于可靠域中,若D∩R≠φ,则焦元D全部或只有一部分居于可靠域中。因此,焦元dk在极限状态方程下的极值定义如下

(12)
若焦元dk的BPA被列入Bel(G)和Pl(G)中,那么gmin-g0和gmax-g0都为正数,满足D⊆G的条件;若焦元dk的BPA在Bel(R)和Pl(R)之外,那么gmin-g0和gmax-g0都为负数,满足D∩R=∅;若焦元dk的BPA可以列入Pl(R)但不能列入Bel(R)中,那么gmin-g0就为负数,gmax-g0则为正数,且满足D∩R≠∅的条件。在计算焦元中的极值时,可以采用极点法减少计算数量。
根据上述可知,证据理论可靠性分析主要过程如下:
1).完成对可靠域R、边缘BPA和X的样本值的确立。
2)对转换成[0,1]均匀变量的样本值进行Kendall系数计算。
3)为选取Copula优质函数,采用贝叶斯方法对各个Copula函数的权重进行计算。
4)上述方程中,采取式(4)完成联合BPA的构建。
5)计算极限状态下的每个焦元极值并分析,从中获取可靠性区间[Bel(G),Pl(G)]。
4 实验与分析
为了验证基于Copula函数模型的构件软件可靠性预测方法的整体有效性,需要对其进行检测。
采用基于Copula函数模型的构件软件可靠性预测方法(方法1)、基于组合模型的软件可靠性预测方法(方法2)和基于体系结构的软件可靠性预测方法(方法3)对构件软件可靠性进行预测。图5为预测时间延迟对比结果。

图5 时间延迟对比图
当方法1、方法2和方法3经过迭代次数的增加进行构件软件可靠性的时间延迟测试时,由图5可知,方法1的时间延迟比方法2和方法3的低,而方法2和方法3的时间曲线波动剧烈,时间延迟大。由此可知,方法1的构件软件可用性比方法2和方法3高,因为该方法对软件缺陷进行分析,根据分析结果实现预测,减小了预测所用的时间,进而降低了时间延迟。
图6为CPU开销对比结果。

图6 CPU开销对比图
采用方法1、方法2和方法3对构件软件可靠性预测中的CPU开销进行测试,综合图6中的数据可知,三个方法中,方法2的CPU开销最大,方法1的CPU开销低于方法2和方法3,说明构件软件在系统运行中产生的能耗小,因为方法1对建立的失效模型进行有效分析,明确了软件故障的前后因素,降低了系统能耗,减少了CPU开销。
表2为平均路径覆盖率对比结果。
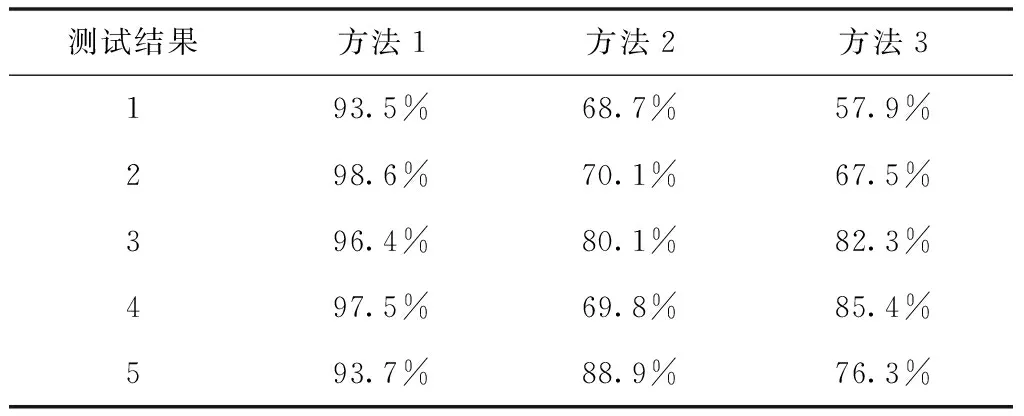
表2 平均路径覆盖率对比
共选取三个方法中的五组平均路径覆盖率测试结果进行对比,分析表2数据可知,方法3在测试路径杂乱的情况下,1、2、5组测试路径覆盖率偏低,最低数据为57.9%,最高数据为85.4%;方法2在路径覆盖率测试中,1、4组覆盖率最低,其余路径覆盖率适中;而方法1在五次测试中路径覆盖率全部高于90%,最高覆盖率达到98.6%,对比方法2和方法3,该方法的路径覆盖率极高。因为方法1解析了软件故障的主要原因,为可靠性预测提供了详细的信息基础,使其能够更全面地对路径进行覆盖,进而提升了平均路径覆盖率。
5 结束语
当构件软件在计算机领域中的容错率大大降低时,构件软件可靠性预测就成为信息技术中必不可少的一部分。根据传统方法在可靠性预测中存在的问题,在此提出基于Copula函数模型的构件软件可靠性预测方法。通过对软件缺陷的分析建立缺陷模型,对故障模型进行构件软件可靠性分析后构建一个联合BPA并在证据变量理论中获取最优Copula函数,完成构件软件可靠性预测,提高了构件软件预测的有效性,解决了目前方法中存在的问题,为今后的构件软件可靠性预测提供了重要基础。

