从元认知角度浅谈“线面平行的性质定理”的教学
陈悦 郭敏玲

[摘 要] “线面平行的性质定理”是高中数学重要的知识点,也是教学的难点. 对于发展学生的直观想象和数学抽象等数学核心素养起着重要作用. 在“线面平行的性质定理”的教学中,通过提高学生的数学元认知体验促进他们掌握线面平行的性质定理.
[关键词] 线面平行的性质定理;元认知;教学重难点
研究背景
立体几何是新课程标准的重点内容之一,这部分内容的学习有利于培养学生的直观想象和数学抽象等数学核心素养. “线面平行的性质定理”是立体几何中的一个重要内容,同时也是学生在学习过程中容易出现混淆的一个知识点. 元认知是学习主体在认知活动过程中的自我意识、自我监控、自我调节. 笔者将从元认知角度浅谈“线面平行的性质定理”的教学,帮助学生更好地掌握这个知识点.
数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养[1]. 我们知道现实的物体都是三维的,要研究现实中的数学问题,把物体抽象化是不可避免的,即点、线、面这些都是抽象化的产物. 直观想象是借助于几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养[1]. “线面平行的性质定理”指一条直线a与一个平面α平行,过直线a的平面β若与平面α相交于直线b,则直线a与直线b平行. 学生利用这个性质定理时,往往会与“线面平行的判定定理”混淆. 在教学过程中,应注重学生的学习感知,唤起学生数学元认知体验,让学生充分调动自己已有的知识经验和学习的主观能动性,克服困难,建立起新旧知识的桥梁,把新知识内化成自己知识体系的一部分.
案例分析
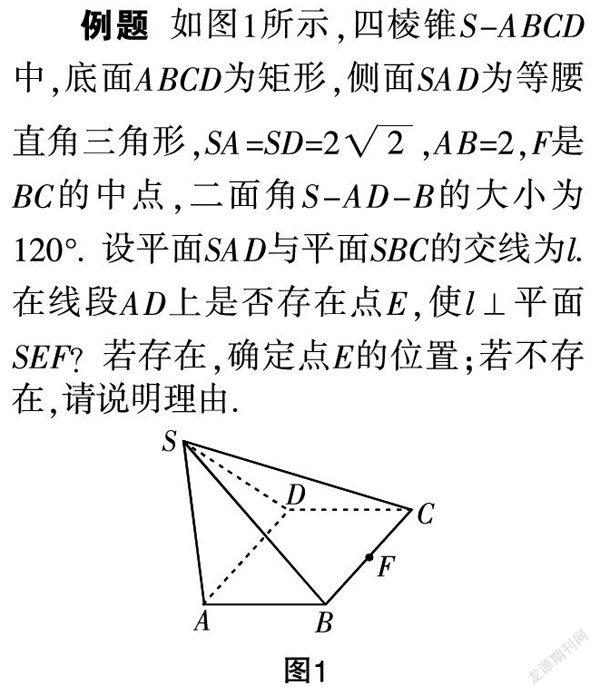
例题 如图1所示,四棱锥S-ABCD中,底面ABCD为矩形,侧面SAD为等腰直角三角形,SA=SD=2,AB=2,F是BC的中点,二面角S-AD-B的大小为120°.设平面SAD与平面SBC的交线为l. 在线段AD上是否存在点E,使l⊥平面SEF?若存在,确定点E的位置;若不存在,请说明理由.
笔者在课堂上以限时测试的形式对所任教的两个班级的学生进行了测试,测试完成后,隔天在课堂上进行了讨论和评讲. 通过测试的结果来看,发现学生出现较多错误的地方有以下几个:(1)出现线面平行的性质定理与线面平行的判定定理的混淆;(2)表述线面平行的性质定理时不够规范准确;(3)无法找出平面SAD与平面SBC的交线l;(4)不能利用AD与l平行这个条件来证明l⊥平面SEF.
为了更好地解释学生在解题中出现的错误,笔者将结合典型的实践案例进行说明. 为了在案例说明中不泄露学生的隐私,通过扫描学生的答案进行了案例展示.
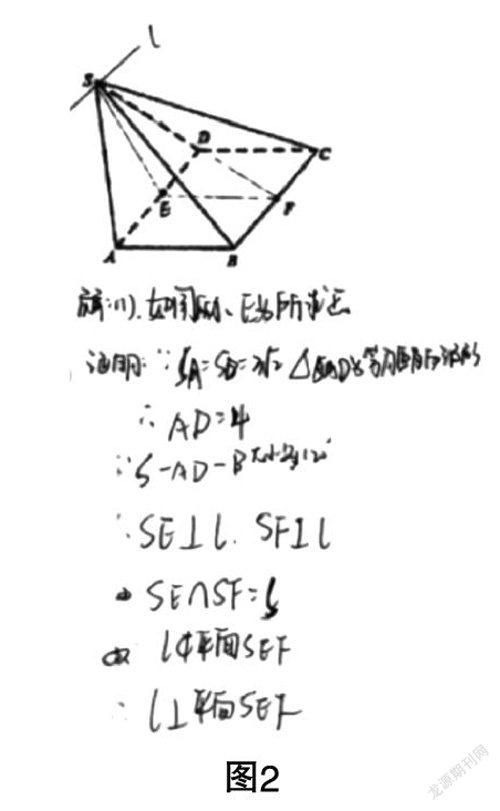
案例1 (如图2所示)从这名学生的答案可以发现,其作了一条过点S的直线l,在解答过程中得出了l⊥SE,l⊥SF,指出l⊥平面SEF,但是没有说明l为什么是平面SAD与平面SBC的交线,也就不能找到一条平行于l的直线来证明本题的结论. 因为本题要证明的是l⊥平面SEF,是不能直接一步到位的. 另外,这名学生的答案虽然标识出了点E,但是在证明过程中并没有指出点E位于线段AD的何处. 很明显,这名学生只是把题目中可以提取到的几何对象进行了简单结合,并没有真正地理解线面平行的性质定理. 对线面平行的性质定理的理解需要直观想象素养,这是一个动态系统,而不是简单结合或者拼凑. 应该把现实中的物体基于图形的运动、变换和位置关系进行感知后,在学习者头脑中进行加工改造形成“几何图形”的表象,再借助于图形分析和相关的公理、定理等解决问题. 在教学中,应当提高学生的元认知体验,经历概念的形成过程,加强对概念的理解,理清概念之间的关系,不要出现概念混淆.
案例2 (如图3所示)这名学生的解答过程是先假设线段AD上的中点E符合条件,利用等腰直角三角形的性质得到SE⊥AD;接着连接SE,SF,利用二面角的定义指出平面SDA与平面SBC的二面角的大小;然后开始说明l是平面SDA与平面SBC的交线,但他的表述是错误的,而且表达过程也不够准确. 首先,这名学生在说明l与平面SAD的关系时,用的符号是“∈”,而正确的符号应该是“?奂”. 说明这名学生没有检查结论,在学习过程中缺乏自我监控. 因此在教学过程中,要创设一些情境,让学生意识到检查的重要性,通过不断强化,让学生在学习过程中保持一种自我调节和自我监控的状态. 其次,这名学生直接写出了l与AD,BC平行,结合他后面给出的解答步骤可以看出,他并不能用数学语言表达出线面平行的性质定理. 他后面给出的答案是围绕l∥AD展开的,所以这名学生知道要证明本题的结论需要证明AD⊥平面SEF. 这名学生对线面平行的性质定理的掌握不到位,他的脑海中可能存在着一定的表象,但是并不能把这些表象之间存在的关系利用准确的数学符号语言表达出来.
在第二天的课堂评讲中,笔者把这两名学生的答案作为引例给了出来,让学生通过一系列的讨论和思考完善了这个定理.
教学建议
1. 通过教学引导,让学生产生数学元认知体验
课堂教学中,我们应当通过创设容易引起学生元认知体验的教学情境,让学生产生数学元认知体验. 在评讲这个题目时,笔者选择了學生的错误解法作为引例,当学生看完错误解法后,很快就发现了解答过程中出现错误的地方,但自己在解答时却没有意识到自己也犯了同样的错误. 有效的课堂教学导入是让学生产生数学元认知的重要条件. 我们可以通过有效的引例,充分调动学生头脑中解决问题所需要的数学知识、解题经验以及数学思想方法等. 接下来通过进一步引导,可以激发学生产生更深刻的元认知体验.
2. 增强数学元认知体验,凸显数学问题的核心
在本节课之前,笔者看到了章建跃先生写的《在一般观念引领下探索空间几何图形的性质(续)——“立体几何初步”内容分析与教学思考》,文章提到了关于线面平行的性质定理的教学,要加强知识之间的联系得出其他的猜想,应当让学生明白这个性质定理是如何被发现的[2]. 笔者觉得这是非常有道理的,对结论的猜想应该是学生通过自己思考得出的,不管猜想正确与否,这都是学生数学学习过程中的一次体验. 如果学生验证正确,这将帮助他们树立学好数学的信心;如果学生验证错误,这个错误也有利于他们接下来的学习. 所以对这节课重难点的处理应该是引导学生去发现这个结论:平面α外一条平行于平面α的直线a与平面α内任意一点形成一个平面β,若有α∩β=b,那么b∥a. 这样一来,学生对平面β的理解就不会那么突兀了,教师也可以更好地处理本节课的重难点了.
3. 加强数学学习过程中的自我调节、自我监控
“在学习活动进行的过程中,要指导学困生学会不断检查、反馈和评价学习活动进行的各个方面,分析发现学习活动中存在的问题及其原因,调整学习行为和学习方法,这样才能提高学困生的元认知水平.”[3]在学习过程中应该充分发挥学生学习的能动性,克服学习过程中遇到的困难,培养坚持不懈的意志力以及时刻检查学习成果的习惯. 学生在解决数学问题的过程中,往往会出现各种数学符号语言表达错误的问题. 例如,直线和平面的包含关系,表述符号不是“∈”,而是“?奂”,等等. 如果在平时的课堂教学中,教师能够引导学生对得到的数学结果进行检查或者检验,保持一种自我调节、自我监控的习惯,那么将有利于提高学生的元认知水平.
参考文献:
[1] 中华人民共和国教育部. 普通高中数学课程标准(2017年版)[S]. 北京:人民教育出版社,2018.
[2] 章建跃. 在一般观念引领下探索空间几何图形的性质(续)——“立体几何初步”内容分析与教学思考[J]. 数学通报,2021(03):2-7+21.
[3] 杨玲. 在元认知的角度上探讨初中数学学困生的成因及转化[D]. 湖南师范大学,2007.

