水下锚索动力响应分析及索力识别方法研究1)

韩飞 段尊义

(西北工业大学力学与土木建筑学院,西安 710129)

引言

水下锚索作为浮式平台、风机、以及悬浮隧道[1]等海洋建筑结构的重要支撑和锚固构件,对于实现整个体系的稳定起着重要作用[2-3].由于锚索阻尼、质量和刚度较小,且长期面临着波、浪、流等海洋环境荷载的作用,因此极易在环境荷载作用下发生振动.可见,明晰其动力学行为是保证结构乃至整个体系安全性和适用性的关键.

不同于空气中的拉索,锚索在水体中的振动具有典型非线性特征,容易产生涡激振动[4]、参数振动[5]等非线性振动现象[6],因此有必要准确掌握其非线性动力特性.在对锚索展开动力分析时,首先需要确定其动力学模型.现有研究工作通常采用弹簧模型[7-9]、张紧弦模型[10-11]以及三维有限元[12-15]3 种模型来对锚索进行动力学建模.这些模型在对悬浮隧道系统进行整体分析时具有一定可行性.然而在研究锚索的局部振动问题时,弹簧和张紧弦模型过于简单,难以准确描述锚索的动力学行为;整体有限元模型虽然能够得到可靠的计算结果,但分析效率低、不便于批量化计算.由于锚索本身具有一定的弯曲刚度,尤其当锚索长度较短时,弯曲刚度对结构动力特性的影响将不能忽略.为了充分考虑锚索弯曲刚度、垂度、以及边界约束条件的影响,一个可行的方案是采用轴向受拉的欧拉梁模型进行建模.鉴于此,本文将采用欧拉梁模型对锚索进行建模,建立考虑锚索弯曲刚度、垂度、请教以及内阻尼等多因素影响的运动微分方程,为实现锚索的精细化动力学分析奠定基础.

在求解锚索运动微分方程时,主要解法可分为时域法和频域法两种.时域法主要有集中质量法[16-17]、有限差分法[18]、有限元法[19]以及间断伽辽金法等[20-21];而频域法通常将锚索视作一分布参数系统,通过摄动法得到响应的摄动解.概括而言,时域分析方法放松了对初始解的要求,其本质是通过牺牲计算效率来降低方程求解的难度;频域法则在派生解的基础上进行摄动,通常只需展开少数项即可获得令人满意的精度.综上可见,相比于时域法,频域解法的稳定性更好、计算效率更高,因此本文将继续采用频域方法来研究锚索的非线性动力响应,推导锚索自由振动的摄动解.

在海洋工程结构的服役期间,由于环境荷载多变、复杂,设计和研究人员难以关注结构在每一时刻下的力学行为,因此需要针对那些能够直接或间接反映整个结构安全性和适用性的参数或指标进行重点监测评估.索力是索缆承重结构的一个重要设计参数和监测指标,它能够为锚索提供显著的结构刚度,是保证整个系统安全运营的关键.索力的损失会导致锚索锚固或承重能力的下降甚至失效,从而影响整个系统的安全性,因此有必要对锚索索力进行实时监测.在海洋环境中想要直接测量索力是困难的,和土木工程结构类似,一个通用且可靠的方法是振动法.该方法依据索频和索力之间的函数关系,通过结构的实测加速度响应求得系统自振频率,最后根据索力识别公式反算索力.该方法物理意义明确,应用起来方便可靠,但当索长较大、垂度效应明显时,传统索力识别公式将会带来显著的误差,这一点在下文数值案例分析中也得到了印证,因此需要研究和提出更加准确、可靠的索力识别公式.

综上,虽然研究者们已经对水下锚索展开了不少研究,也取得了一定成果,但动力学建模和求解方法的精度或效率有限,难以满足海洋工程结构的快速、精细化分析需求,亦无法准确揭示此类结构在复杂荷载作用下的非线性动力学特性.鉴于此,本文旨在形成一种锚索非线性动力特性的快速分析方法;推导锚索自由振动响应的摄动解;给出考虑垂度影响后锚索索频的解析表达式;依此对传统索力识别公式进行修正,提出考虑锚索弯曲刚度和垂度影响的索力识别公式.

1 力学模型

如图1 所示,在对一长为l的锚索进行动力分析时,通常将其视为两端铰接的小垂度欧拉梁.EI,m˜,A,H,θ 分别为锚索的截面惯性矩、单位长度线质量、以及有效截面积,索力以及倾角.y(x) 和u(x) 分别为锚索的初始构型和振动位移.一般地,倾角为θ的锚索在速度为v的常流作用受到的拖拽力,锚索在次作用下会产生新的变形(垂度),此时锚索由于弹性伸长将产生附加索力H*.由于这部分附加索力是静力,因此这一部分效应可以一并考虑到初始索力H中去.

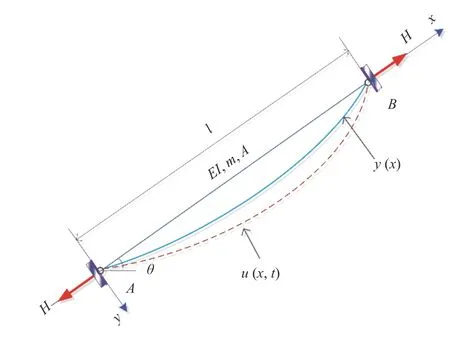
图1 小垂度锚索力学模型Fig.1 Mechanical model of shallow sagged anchor cables

由于强大的轴向拉力的存在,锚索的初始垂度通常较小,因此初始构型通常采用二次抛物线y(x)=4ex/[l(l-x)] 来模拟[22],其中垂跨比e=m˜glcosθ/(8H),g为重力加速度.则在水流作用下,锚索发生自由振动运动微分方程为[23-24]

其中c为锚索的黏滞阻尼系数,h(x,t) 表示锚索在运动过程中由于弹性伸长引起的附加索力,其表达式为[25]

其中CD,ρw,和Dt分别为拖拽力系数,水体密度,以及锚索直径,Cm为水体附加质量系数.

2 理论方法

2.1 自由振动响应求解

式(1)为一具有平方非线性项和积分项的4 阶非线性偏微分方程,其直接求解将十分困难,因此通常的处理办法是用伽辽金离散法[28]将其转化为单自由度的常微分方程,即假设解有如下形式

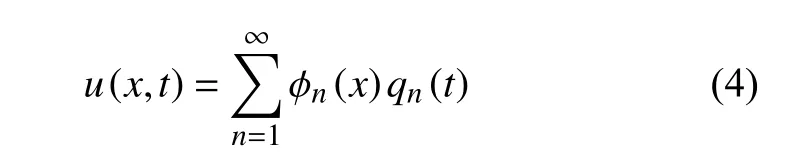
其中qn(t) 为正则坐标,ϕn(x) 为试函数,取结构正则化后第n阶模态振型.

对应于图1 的振型函数 ϕn(x) 可采用标准正弦函数来模拟,即

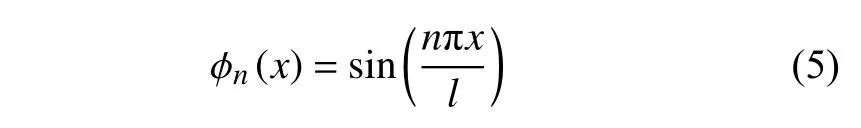
事实上 ϕn(x) 的选择应尽量选用力学模型的精确振型函数.例如,若锚索上端连接的浮体无法视作刚体时,譬如悬浮隧道的管体,采用滑动-弹性支持则能更好的诠释锚索的实际约束条件.那么对于上端弹性支承的锚索,其振型函数 ϕn(x) 应采用下式[29]

若要获得锚索的自振频率和响应,首先需要式(1)分离变量,将式(4)代入式(1)可得

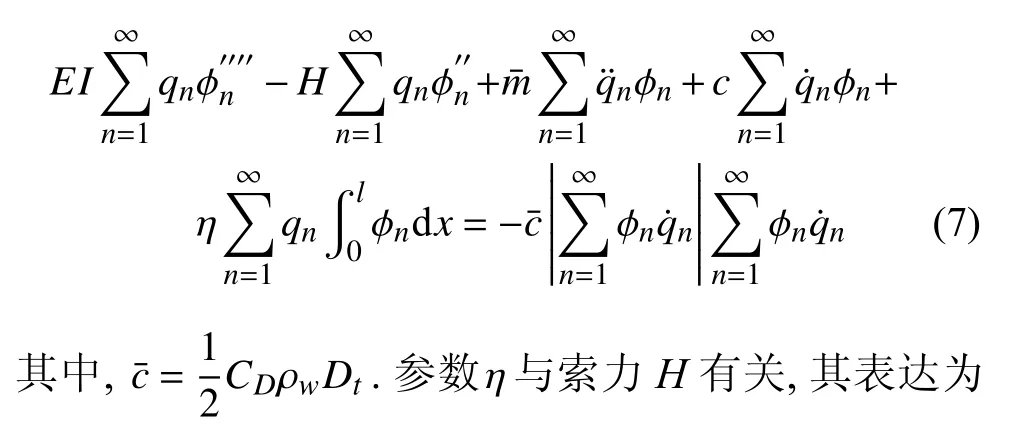
可见,由于式(7)中积分项(附加索力)和平方项(水体阻力)的存在,式(7)为一耦合方程.为了进一步将其化为单自由度系统,需要对方程中的非线性项进行线性化处理.为此,本文采用能量守恒原理,即利用非线性力在一个周期内做的功与线性化后的力做功相等的原理,可将第n阶线性化后的水体阻尼力和附加索力分别写为

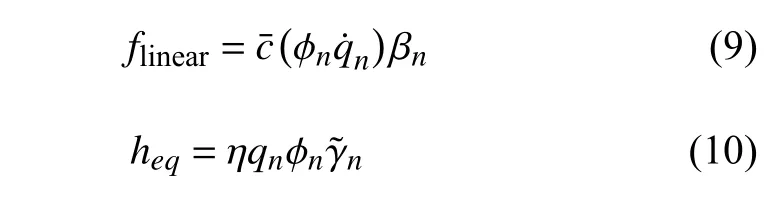
根据二者在一个周期内与其非线性力做的功相等的原理,有

对于式(7)描述的非线性系统,令c==h=0,可得对应派生系统的运动方程为

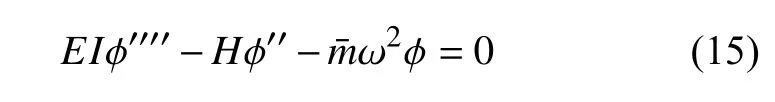
将上式代入式(7)并利用式(11)～ 式(14)有

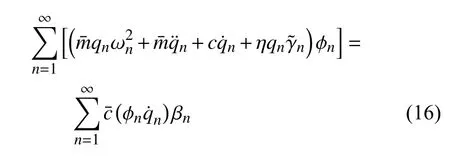
利用振型的正交性,式(16) 两端同时乘以第m阶模态振型 ϕm(x) 并在 (0,l) 范围内积分得

当小参数 ε=0 时,式(18)的解为

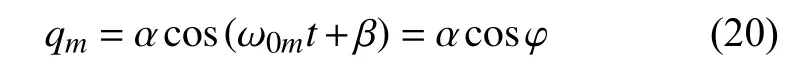
根据平均化方法,幅值 α 和相位 β 应满足

进而可得

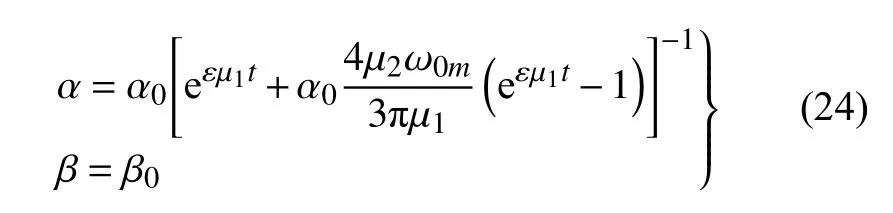
其中,α0和 β0为初始幅值和相位,二者由初始位移v0和速度确定.

2.2 锚索索力精细化识别方法

传统索力识别公式未能考虑索的垂度对频率的影响,得到的索力是不准确的,下文的案例分析也表明了采用传统索力识别公式会导致上百千牛的误差.鉴于此,本节将给出考虑垂度影响后的修正索力识别公式,为此类结构的索力精确识别提供理论依据.

式(19)定量描述了由于垂度引起的几何非线性对系统频率的影响,再次将其写出

式中,η γn为几何非线性对系统自振频率的影响,其中 η 与结构的垂度有关,γn与派生系统的第n阶振型 ϕn有关.需要注意的是,在应用式(25)中的频率单位为rad/s.

实际工程中广泛采用的索力测试方法为振动法,该方法依据索频和索力的一一对应关系,通过加速度传感器或机器视觉手段得到拉索的自振频率,进而由自振频率反解出索力[30].当虑拉索弯曲刚度时,由式(15)表征的两端铰支弹性索的索力可表示为

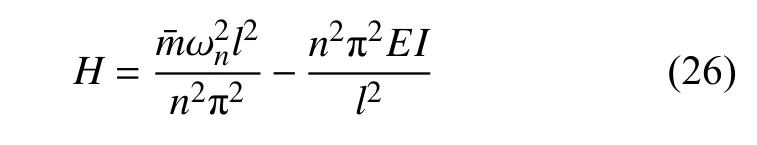
其中 ωn为系统第n阶无阻尼自振频率.

式(26)即为实际工程中通常采用的索力识别公式,事实上它是基于简支梁模型给出的,未考虑垂度效应对频率的影响.换言之,锚索的实测频率由于包含了垂度的影响,并不能直接满足式(26),由此得出的索力H是不准确的.

上式即为本文建议的锚索索力精细化识别公式,其中 γn可由式(14)求得.特别地,对于两端铰支边界有

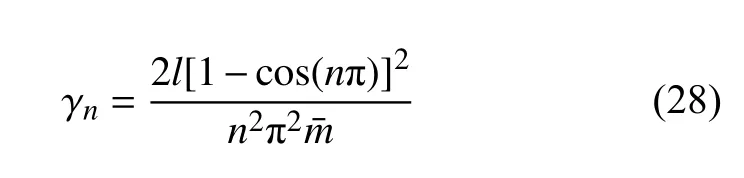
其他边界条件也可依据式(14)预先求出.而参数 η 由于和索力H相关,因此严格意义上式(27)需要进行迭代运算方可解得准确的H,经试验,通常仅需迭代两步即可求得准确结果.考虑到实际情况中远小于H,H微小的变化对 η 之值的影响很小,因此在实际应用时,方便起见可采用设计索力H0,或将 ω0n代入式(26)获得一个估计的索力值,进而求得 η .

综上,锚索的索力识别步骤可归纳为:

(1) 对锚索响应时程做傅里叶变换求得系统模态频率 ω0n;

(2) 将 ω0n代入式(26)估计一个 η˜ 值,并利用式(14)求得 γn;

(3) 将 ω0n,以及 γn代入式(27)计算锚索索力H.

3 准确性验证

本节将针对上文给出的锚索自由振动响应解及索力识别公式进行验证,说明其准确性.取锚索的相关设计参数如下:l=161.11 m,Dt=0.424 m,θ=60°,CD=0.7,E=2 .1×1011Pa,I=0.001 6,m¯=1301.5 kg/m,H=4.04×107N .

3.1 动力响应结果验证

在计算时,无阻尼模态频率 ωn可由直接由式(26) 求得,取一阶模态频率 ω1=0.548 Hz,阻尼比ξ1=0.001 8.将式(5)直接代入式(7)并分离变量可得

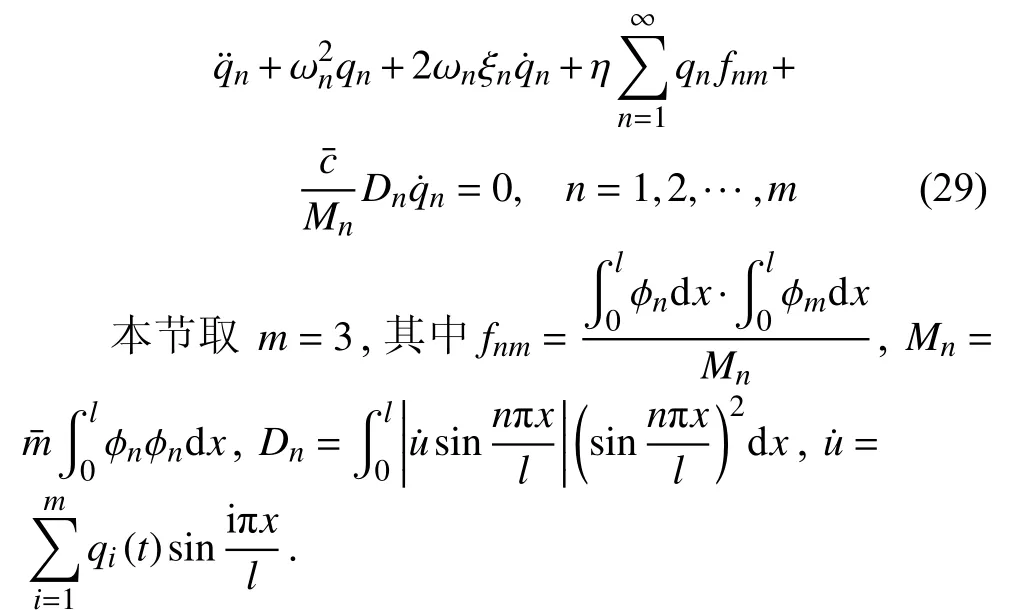
式(29) 通常可借助4 阶龙格-库塔法直接求解,本文则采用Ode45 求解器直接求解.取锚索跨中位置初位移和初速度分别为和,两种方法得到的位移和速度响应时程结果对比见图2 和图3.

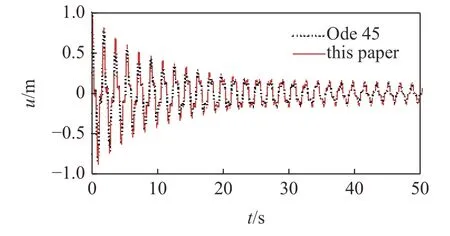
图2 两种方法位移响应时程对比Fig.2 Comparison of displacement response calculated by the two methods

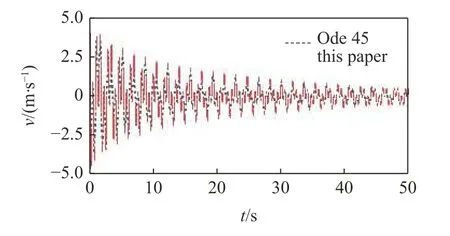
图3 两种方法速度响应时程对比Fig.3 Comparison of velocity response calculated by the two methods

对比可知,本文给出锚索非线性动力响应的解析解与数值解吻合得很好,进而说明了本文方法的准确性.

3.2 考虑垂度影响的频率计算式验证

为了进一步验证本文给出的考虑垂度影响的频率计算式(25)的准确性,对上节求得的响应时程做快速傅里叶变换得到其频谱如下.

由图4 可知考虑锚索垂度效应的一阶模态频率ω01=0.559 9 Hz,明显大于其线性系统的频率ω1=0.548 Hz .可以预见,随着垂度的进一步增大,其对系统频率的影响将进一步增大.

图4 锚索响应频谱Fig.4 Frequency spectrum of the anchor cable

依据式(8)和式(28)式可得到 γ1=0.100 6,将η=4.585 3,将二者代入式(25) 可求得系统频率为0.558 2 Hz,与频谱分析结果0.559 9 Hz 十分接近.由此可见,本文给出的锚索频率估算公式是足够精确的.

3.3 索力识别公式验证

在利用实测频率进行索力识别时,由于参数 η 与索力H相关,因此严格意义上需要进行迭代求解.在确定 η 的迭代初始值时,需要预估一个索力值H0,该值可通过将识别频率 ω01代入传统索力识别式(26)予以确定.收敛准则为,相邻两次迭代结果之差不超过允许误差限,迭代步骤如下.

由表1 可看出,依据本文建议的索力识别式(27),只需两步就能准确的识别出索力值.而第一步迭代结果=4.051×107N与H=4.04×107N 相差仅0.25%,从而验证了本文方法的准确性.需要说明的是,当锚索的其他物理参数随时间变化时,依然可以在其基础上借助优化算法来进行参数识别.例如,基于振动法的索力和直径Dt等参数的同时识别问题,可提成一个单目标最优化问题

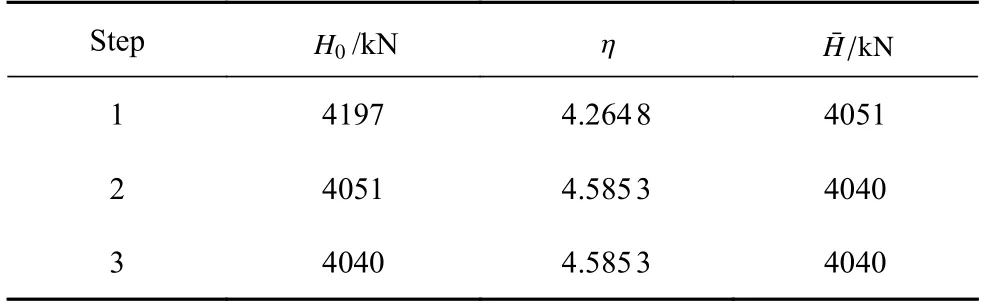
表1 索力识别迭代过程Table 1 Iteration of cable force identification

s.t.ωj≥ωi＞0,j＞i,i=1,2,3,···

其中,f为优化目标函数.上式本质上是将拉索的索力和Dt识别问题转化为寻找一组H和Dt,使由此计算出的第i和j阶频率与实测频率 ωi和 ωj的离差最小,i和j通常可取1 和2.若能测到更多阶频率信息,则式(30)表征的优化问题可得到更加准确的识别结果.由于频率和结构参数的关系已经由式(27)解析给出,因此采用常规的梯度类优化算法即可实现多个时变参数的动态识别.

值得注意的是,第一步索力迭代的初始值H0=4.197×107N 即为传统公式(26)的识别结果,其与真实值相差高达1579 kN,难以用于结构的精细化分析和监测.为了进一步说明垂度对索力识别误差的影响情况,图5 给出了垂跨比e(通过改变索力H)的变化对锚索索力识别误差 δ 的影响曲线.可以看出,随着拉索垂跨比增大,采用传统索力识别方法的误差线性增大.特别地,当垂度为0.004 时,索力识别结果的绝对误差将达到2409 kN,而相对误差为7%.可以预见,识别误差还会随着垂度的增大进一步增加.因此,在实际应用中必须计入垂度对频率进而对索力的影响.

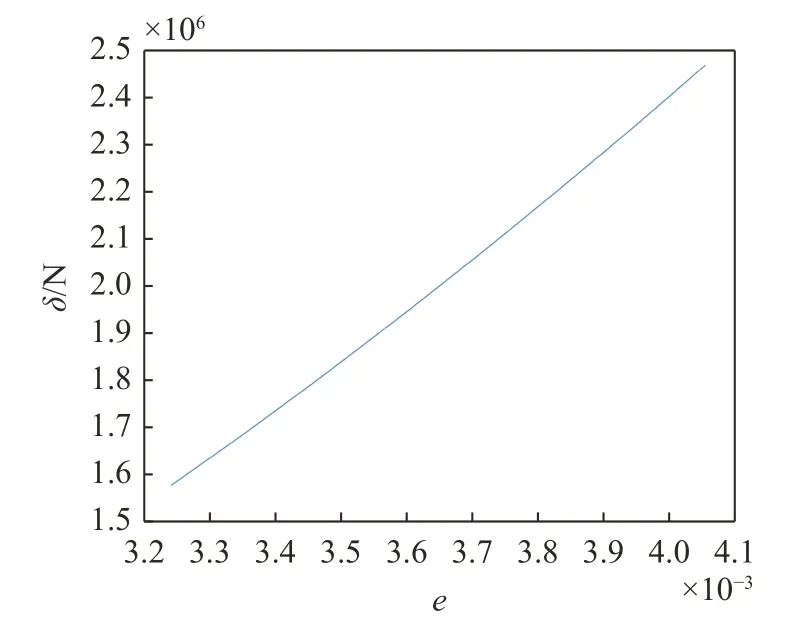
图5 拉索垂度对索力识别误差的影响曲线Fig.5 Effect of sag on cable force identification error

4 结论

本文针对一类水下柔性张拉锚索结构,采用等效线性化方法和摄动方法推导了锚索的非线性动力响应的摄动解;给出了考虑垂度影响的锚索频率计算式,从而定量描述了非线性因素对频率的影响;通过与数值解对比验证了结果的准确性.依据索频计算式对传统索力识别公式进行了修正,数值案例研究证明了该修正公式能准确求得锚索索力.相反,采用传统公式识别出的索力与真实值相差1579 kN.可见,本文建议公式能够实现锚索索力的精确识别和实时监测,进而为水下锚索的运营期健康监测和状态评奠定了理论基础.

事实上,海洋锚索是一类特殊的小垂度索结构,它与陆路中的小垂度索,本质差别在于所处的力学环境不同,及在研究其自由振动问题时需要考虑水体阻力及附加质量的影响.若将这两部分影响忽略,则退化为更一般的小垂度索的场景.因此,本文给出的索力识别公式考虑因素更为全面,完全可以推广到更加一般的小垂度索结构.