超精密微小型车铣复合加工机床的空间误差建模与灵敏度分析＊

郑中鹏 金鑫 郭嘉靖 高瑞麟 井浩 李二波

（①清华大学机械工程系，北京 100084；②北京理工大学机械与车辆学院，北京 100081）

随着尖端科技和国防工业的不断发展，微小型复杂结构件的加工精度要求越来越高。但是，机床在实际加工运动过程中与理想运动存在偏离状态，导致刀具运动轨迹偏离设定的目标位置，进而产生加工几何误差，降低了工件的加工精度[1]。因此，开展加工误差建模与补偿是必不可少的。

误差建模是机床的各项误差参数与工件精度之间的数学关系，属于误差补偿核心的部分。Schultschik R 在1977 年首次提出了机床空间误差概念，并且采用闭合矢量链方法表达精密三轴坐标镗床的误差，为日后的学者研究加工误差奠定了基础[2]。天津大学的刘又午等人开展了多体系统动力学理论研究，提出了一种基于多体系统理论（MBS）的机床运动几何误差模型[3]。张宏韬等人提出一种定量表达机床各轴在运动过程的位置误差模型，进一步给出分步解耦补偿方法和机床的误差补偿数学模型[4]。同时，针对加工过程热引起的机床热变形降低加工精度的问题，Chen J S 等人以高精密机床静压主轴为研究对象，研究影响主轴精度的热因素，通过有限元分析，计算主轴相关热量参数[5]。上海交通大学项四通等人基于螺旋理论提出了五轴机床的空间误差建模和补偿策略，建立空间误差统一模型，并在多台试验机床上进行了验证[6]。北京工业大学范晋伟等人开展了复合数控机床几何误差建模与灵敏度分析，识别了影响机床加工精度的关键性几何误差[7]。

超精密车铣复合加工机床与传统的加工机床相比，车铣复合加工机床一般有2 个旋转轴，3～5 个直线轴，甚至更多直线轴。更多的旋转轴和直线轴的组合意味着机床存在更复杂的误差补偿模型关系。因此，为了进一步提高超精密车铣复合加工复杂微小型构建的精度，指导和优化机床结构设计，本文以北京理工大学自主开发的超精密车铣复合加工机床CXKG25-I 为研究对象，基于多体系统理论，建立超精密车铣复合加工机床空间几何误差模型，并对机床进行误差灵敏度分析，获得影响加工精度的关键误差因素。

1 超精密车铣复合加工机床结构分析

针对三维复杂微小型结构件的高精度加工需求和车铣复合功能特点，北京理工大学微小型制造研究所自主开发了超精密车铣复合加工机床CXKG25-I[8]，其结构、实物分别如图1、图2 所示。该机床包括X、Y、Z这3 个微米级精度宏动轴，U、W两个亚微米级精度直线轴，旋转B轴和旋转C轴，可实现七轴五轴联动复杂结构件加工。此外，为了实现加工零件的在位实时补偿功能，机床上安装有在位测量系统，可实时检测零件尺寸。

图1 超精密车铣复合加工机床CXKG25-I 结构

图2 超精密车铣复合加工机床CXKG25-1 样机

目前，广泛使用多体系统理论开展空间几何误差建模，这种方法通用性强，是一种比较成熟的建模体系。该理论将机床部件抽象为机床误差信息的刚体，每个刚体对应一个部件系统，可以建立超精密车铣复合加工机床的各个拓扑结构，并采用矩阵反映各个系统之间的联系，机床各个部件元素通过机床尺寸链反映刀尖轨迹[9]。如图3 所示，超精密车铣复合加工机床CXKG25-I 的尺寸链可以分为工件链、刀具链和运动链，具体传递链可表示为：

图3 超精密车铣复合加工机床运动链

（1）床身到工件：“床身0→直线导轨X轴1→直线导轨Y轴2→旋转C轴3→工件W轴4”。

（2）床身（基座）到刀具：“床身0→直线导轨Z轴5→直线导轨B轴6→直线导轨U轴7→直线导轨W轴8→刀具9”。

2 超精密车铣复合机床空间几何误差元素分析

根据ISO 230-1 和ISO 230-7 的定义，机床的几何误差主要取决于位置相关的几何误差（PDGEs）和位置无关的几何误差（PIGEs）[10]。其中，位置相关的几何误差（PDGEs）指的是各个直线轴、旋转轴自身存在的位置误差；位置无关的几何误差（PIGEs）主要指的是各个轴间的垂直度误差。此外，由于机床每个运动轴均可以视作刚体，具有6个自由度，所以存在6 项基本几何误差，包括3 个线性几何误差和3 个旋转角度误差；对于平动轴，线性几何误差根据移动方向可以分为定位误差和直线度误差，角度误差根据绕不同轴旋转方式，可以分为俯仰误差、偏摆误差和滚摆误差[11]。

如图4 所示，以超精密车铣复合机床Z轴几何误差分析为例，Z轴包括3 项线性平动误差，分别是Z方向的定位误差δz(z)，X方向的直线度误差δx(z)和Y方向的直线度误差 δy(z)。3 项角度误差分别是绕X轴旋转的俯仰误差εx(z)，绕Y轴旋转的偏摆误差εy(z)和绕Z轴旋转的滚摆误差 εz(z)。由于超精密车铣复合机床CXKG25-I 为七轴五联动复合加工机床，有5 个直线轴，共30 项位置相关的几何误差（PDGEs）。

图4 超精密车铣复合加工机床Z 轴几何误差元素

如图5 所示，对于旋转轴而言，同样存在6 项误差几何项目，包括3 项线性误差和3 项角度误差。根据静压主轴的形状和坐标关系，具体的误差项目分别为C轴轴向定位线性误差 δz(c)，X轴方向的径向线性误差 δx(c)，Y轴方向的径向线性误差 δy(c)，绕Z轴方向旋转的C轴定位角度误差 εz(c)，绕X轴方向倾斜的角度误差 εx(c)和绕Y轴方向倾斜的角度误差 εy(c)。需要指出的是，超精密车铣复合加工机床共有B轴和C轴2 个旋转轴，因此共有12 项位置相关几何误差(PDGEs)。

图5 超精密车铣复合加工机床的C 轴几何误差元素

图6 是超精密车铣复合加工机床的垂直度误差元素示意图，其中5 个直线轴两两之间存在8 项垂直度误差，分别是 γxy、γyz、γxz、γuy、γuw、γuz、γwx、γwy；直线轴与旋转轴之间存在7 项垂直度误差，分别是γxb、γzb、γub、γwb、γcx、γcy、γcu，因此共有15 项垂直度误差(PIGEs)。

图6 超精密车铣复合加工机床的垂直度误差元素分量

综上，超精密车铣复合加工机床CXKG25-I 所有的空间几何误差因素如表1 所示。

表1 超精密加工机床的几何误差元素

3 超精密车铣复合机床空间误差建模

在多体运动学理论中，任意两个相邻的刚体之间的误差包括位置矩阵、位置误差矩阵、运动矩阵和运动误差矩阵[12]。此外，如果不考虑位置误差和运动误差的话，任意两个相邻刚体之间的关系可以表示为，刚体i与相邻的刚体j之间的转换矩阵具体表示如下。

根据表达式（1）,工件尺寸链的传递矩阵如下。

根据表达式（1），刀具尺寸传递链的矩阵如下

此外，如果没有机械加工误差，则理想刀尖轨迹模型如下。

因此，机床加工误差模型可以表示刀尖真实轨迹模型减去理论刀尖轨迹模型

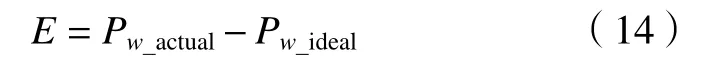
4 误差灵敏度分析

机床加工误差补偿可以在一定程度上提高车铣复合加工零件的几何精度。但是，由于影响机床加工精度的误差因素有57 项，对其所有的误差辨识和补偿相当复杂，因此需要建立灵敏度误差分析模型，确定影响超精密车铣复合加工过程中的关键误差因素。目前，一阶灵敏度函数方法是工程计算中使用比较多的一种误差灵敏度分析方法[13]，求出对各个方向的偏导数，得到数控机床传动机构各个误差的灵敏度，计算表达式如下

为了可视化分析与对比，将灵敏度数值归一化，并计算并得到所有误差的灵敏度系数。需要指出的是，误差灵敏度系数在X轴、Y轴和Z轴3 个方向的各个误差分量之和等于1，具体表达式如下

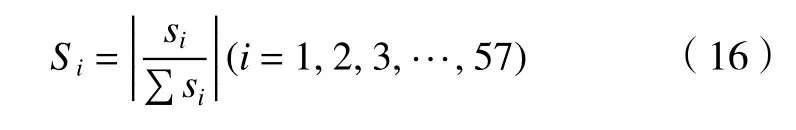
此外，在超精密车铣复合加工机床中，常常采用正交切削加工。因此，本研究中以主轴和铣削主轴垂直布局来设置初始位置参数，具体参数如表2和表3 所示。

表2 超精密车铣复合加工机床的初始位置

表3 超精密车铣复合加工机床各种间初始参考位置

由图7 可知，正交车铣过程中影响X方向加工误差(Ex)的关键误差主要包括X轴绕Y轴的偏摆误差 εy(x)，Y轴自身的滚摆误差 εy(y)，Z轴自身的滚摆误差 εz(z)，C轴绕Y轴的偏摆误差 εy(c)，B轴绕Z轴的偏摆误差 εz(b)，以及XZ、XB、CX和CU轴间的垂直度误差,这些关键误差的敏感度系数之和为76.91%,每个误差源的灵敏度系数均在7%以上。

图7 空间几何误差在各个误差方向的灵敏度系数(Sx=10 mm，Sz=10 mm)

正交车铣过程中影响Y方向加工误差(Ey)的关键误差主要包括X轴绕自身的滚转误差 εx(x)，Y轴绕X轴的俯仰误差εx(y),C轴绕X轴的俯仰误差 εx(c)，以及YZ、CY轴之间的垂直度误差。这些关键误差的灵敏度系数均在12% 以上，其敏感度系数之和为60%。

最后，影响正交车铣过程中影响Z方向加工误差(Ez)关键误差主要包括Z轴绕X轴的俯仰误差εx(z)和B轴绕X轴的俯仰误差 εx(b)，这两个关键误差源的灵敏度系数超过12%。此外X轴绕Y轴的俯仰误差 εy(x)，Y轴绕自身的滚摆误差，W轴绕Z轴的滚摆误差 εz(w)，C轴绕Z轴的滚摆误差εz(c)，C轴绕Y轴的偏摆误差 εy(c)等误差项也对结果具有一定的影响。需要注意的是，相比平动误差而言，综合误差受到角度旋转误差分量和各轴间的垂直度误差分量的影响更大，因此在后续加工误差补偿过程中优先考虑角度旋转误差和垂直度误差的影响。

此外，加工过程中，各个运动轴的位置和姿态不断改变，零件和刀具的位置也随之不断变化，综合误差模型的关键灵敏度系数也在不断变化，为了进一步揭示获得的关键误差分量对加工精度的影响，以常用低刚度结构件（挠性接头 200 mm×200 mm以内）加工的范围内进行灵敏度分析。图8、图9分别是固定X轴、移动Z轴（200 mm），固定Z轴、移动X轴（200 mm）的灵敏度分析，与图7 相比较，角度旋转误差和垂直度误差仍然是影响综合误差的重要因素。但是，需要注意的是部分误差项目随着初始位置不同发生了变化，比如Z轴绕X轴俯仰误差 εx(z) 随着Z轴的移动（Sz=200 mm）而变化，这主要归因于行程增加使Z轴部件的制造误差、装配误差和伺服控制误差增加导致的。

图8 空间几何误差在各个误差方向的灵敏度系数(Sx=10 mm,Sz=200 mm)

图9 空间几何误差在各个误差方向的灵敏度系数(Sx=200 mm,Sz=10 mm)

5 结语

（1）分析了超精密车铣复合加工机床CXKG25-I的57 项几何误差元素，其中包括42 项运动误差和15 项垂直度误差，建立了超精密车铣复合加工机床的空间几何误差补偿模型。

（2）获得了影响加工误差因素的关键几何敏感误差因素。研究表明：相比较平动线性误差而言，机床加工精度受到角度旋转误差分量和垂直度误差分量的影响更大。