动态反演方法进行路面结构性能衰减分析的可行性

曹丹丹， 朱 铭， 张 嘉， 张金喜， 赵延庆

(1.北京工业大学城市建设学部， 北京 100124； 2.大连理工大学交通运输学院， 大连 116024)

精准预测在役路面结构性能的衰变行为对通过维养提升路面使用性能以及延长路面寿命具有重要指导性作用[1-2]. 室内测试手段无法真实模拟路面材料的实际受力状态，测试结果无法客观地反映筑路材料在实际服役环境下的性能[3]. 落锤式弯沉仪(falling weight deflectometer, FWD)能够模拟行车冲击荷载，并得到不同位置处的弯沉时程曲线，为路面质量评定和养护决策制定提供了基础数据[4]. Gedafa等[5]基于现场FWD测试结果，利用Sigmoid函数建立了荷载中心处的弯沉峰值和剩余寿命的关联模型. 然而，该模型仅采用路面结构整体强度作为分析指标，无法解释结构内部各层位力学参数的衰减和剩余寿命的关系. 采用FWD实测弯沉，通过反演手段确定筑路材料的力学参数，能够更加客观反映材料的实际性能，而且可以和路面力学分析有效衔接.

目前，成熟的路面力学参数反演软件中，大部分采用层状弹性理论计算路面弯沉或形成数据库[6-7]，反演得到各结构层的弹性模量. 沥青混合料力学性能具有明显的荷载频率和温度依赖性，而且FWD的荷载作用时间极短，接近于冲击荷载，荷载和筑路材料的特性导致动、静态方法分析得到的路面弯沉误差可达40%以上[8]. Lee等[9]收集了不同时期内的现场弯沉测试结果，采用动态方法反演得到沥青层的动态模量主曲线和其他层的弹性模量，结果表明筑路材料的力学参数随着路面服役时间的延长会逐渐减小，然而在分析中忽略了路面力学响应的变化.

本文以山西大新高速公路典型的半刚性基层和柔性基层沥青路面结构作为研究对象，收集了不同服役时长的路面弯沉实测数据. 分别采用动、静态方法反演得到各结构层的力学参数，分析反演参数随结构服役时间的变化趋势. 然后，采用动态反演力学参数计算了移动荷载作用下的路面力学响应，并分析了其在服役期间的变化，验证了动态反演方法在路面结构性能衰减分析中的可行性.

1 力学参数反演

路面力学参数反演过程由正分析过程和优化过程两部分构成. 首先，利用正分析方法得到弯沉理论计算结果；然后，在优化过程中以弯沉计算值和实测值的误差建立目标优化函数，通过不断修正路面力学参数以保证弯沉误差满足计算精度要求[10]. 本文在沥青路面动态黏弹分析中采用谱单元法，因此，下面对谱单元法进行简单介绍.

1.1 正分析方法

谱单元法以波动理论为基础，其结构控制方程[10-12]为

(1)

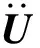
谱单元法在分析过程中，利用傅里叶变换对响应控制方程进行时间和空间变换，在频率- 波数域内对控制方程进行求解，不需要对路面结构层进行划分，大大地提高了正分析的计算效率，并采用双节点谱单元描述有限厚度的结构层，采用单节点谱单元描述半空间无限厚度土基. 在频率- 波数域内，根据亥姆霍兹定理，将荷载应力波分解为径向的膨胀波和竖向的剪切波，对分项波动方程进行推导得到谱单元节点的位移解析表达式. 根据路面结构荷载和边界条件，建立谱单元的刚度矩阵以及结构总体刚度矩阵，求解得到该域内的位移结果. 将不同频率- 波数域内的结果相加，利用傅里叶逆变换可以得到时域内的力学响应. 具体的计算方法见文献[11-14].

谱单元方法中将沥青层作为黏弹性材料，其他结构层作为弹性材料. 本文采用修正的Havriliak-Negami(modified Havriliak-Negami，MHN)模型[15]描述沥青混合料的黏弹性力学行为，公式为

(2)

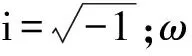
1.2 参数优化过程

路面力学参数优化过程关键在于建立目标优化函数，在传统的静态反演方法中，通过采用各传感器测量弯沉峰值构成的弯沉盆建立目标优化函数，忽略了时程曲线中包含的大量信息，如不同位置处弯沉峰值时间和响应黏滞信息等[9,16-17]. 在动态反演方法中，利用不同位置处弯沉时程曲线的实测值和计算值的均方误差建立目标优化方程

(3)

式中：F为目标优化函数；K为传感器个数；N为各传感器收集的弯沉数据长度；dcal,i,j和dmea,i,j分别表示第i个传感器、第j个弯沉的计算值和实测值.动态反演方法能够更全面采用时程曲线中的有效信息，在参数优化过程中提供更多的约束条件，保证反演力学参数趋于真实值.

2 弯沉测试及典型反演结果

2.1 测试路段信息

现场弯沉测试在山西大新高速公路不同基层类型的路段上进行，本文选取了2段路面结构，分别为半刚性基层路面结构A和柔性基层路面结构B. 路面结构A各层的级配及材料类型为：4 cmAC-16+5 cmAC-20+6 cmAC-20+16 cm水稳碎石+14 cm三灰碎石+20 cm水稳砂砾+土基；路面结构B各层的级配及材料类型为：4 cmAC-16+5 cmAC-20+6 cmAC-20+15 cmATB-30+35 cm级配碎石+土基. 在路面分析和参数反演中，为了便于分析和提高计算效率，根据各结构层材料的特性，将路面结构简化为4层路面结构，各结构层厚度及物理参数如表1所示[18-19].

表1 路面结构信息

2.2 力学参数典型反演结果分析

现场弯沉测试在不同时间进行，测试荷载峰值均设定为0.7 MPa，荷载作用半径为0.15 m，弯沉传感器距荷载中心的距离分别为0、0.33、0.50、0.80、1.10、1.40、1.70 m. 本文收集了2007年、2010年和2015年的实测弯沉数据. 经调研，大新高速于2010年统一进行了罩面养护，2017年由于各路段病害类型不同，采用了不同的养护措施，为保证分析弯沉测试环境及路面状况的一致性，本文选取2010年和2015年的弯沉数据进行力学参数反演，2010年罩面厚度为2.5 cm，并在后文分析中对面层厚度进行修正.

本文动态反演方法如前文所述，静态方法采用软件EVERCALC进行[6]. 为分析动、静态反演结果的差异性，选取了2010年典型测试结果分别进行动、静态反演，反演结果如图1、2所示.

图1 动态反演结果Fig.1 Dynamic backcalculated results

图2 静态反演结果Fig.2 Static backcalculated results

由图可知，动、静态方法反演得到的弯沉均能很好地吻合实测弯沉曲线，这表明反演得到的路面动、静态力学参数均能表征路面结构在荷载下的力学行为. 2种方法的反演结果如表2所示，可见动态方法得到了沥青层的MHN模型参数，以及其他结构层的弹性模量. 有了MHN模型参数，就可以得到沥青层的动态模量|E*|和相位角主曲线，如图3所示. 图中主曲线的参考温度为测试现场实际温度(28 ℃)，fr为缩减频率. 静态反演方法仅仅得到筑路材料单一弹性模量值，与动态反演方法存在一定差异，基层和土基的静态反演结果比动态反演结果分别大70%和40%以上，而底基层的静态反演结果比动态反演结果小30%左右. 由图3可见，动态模量和相位角主曲线可以描述沥青混合料力学特性随荷载频率的变化趋势，比单一的弹性模量能更全面地描述沥青混合料的温度、荷载频率的依赖性[15,20].

表2 典型结构层反演模量

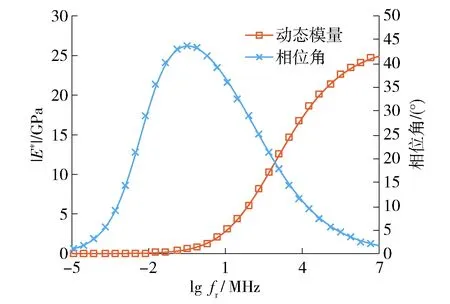
图3 沥青层复数模量主曲线Fig.3 Complex modulus master curve of asphalt layer

3 反演结果分析

本文以2010年和2015年实测弯沉作为力学参数反演的基础数据，在反演过程中，对2010年数据采用人工调试的方法，获得反演结果的初始值. 然后，以2010年反演结果的平均值作为2015年力学参数反演的初始值，对比分析2010年和2015年的反演力学参数的衰减演变规律. 在分析中，根据测试点的桩号位置，选取同一桩号的测试结果作为对比对象，而且分析测试点位置处路表没有明显的病害. 其中半刚性基层路面结构A共有11个测点，柔性基层路面结构B共有6个测点. 为避免测试温度对反演结果的影响，在对比分析中，将沥青层的反演结果统一转化为20 ℃下的模量进行分析[21-22].

3.1 半刚性基层路面结构

由上述内容可知，通过动态反演得到沥青层的复数模量. 为便于定量分析，计算了沥青层在温度为20 ℃、荷载作用频率为10 Hz时的动态模量. 图4给出了动态反演参数随测点桩号的分布结果.

由图可知，通过动态方法反演得到的不同测点的结构层模量虽然表现出一定的波动性，但是反演得到的2015年各结构层的模量值均小于2010年结果，表明相对于2010年， 2015年各结构层强度均有一定的衰减. 土基层反演结果的变化程度明显小于其他结构层，表明面层、基层和底基层的强度衰减程度明显大于土基，尤其是8号测点的反演结果，面层、基层和底基层的模量减少了50%以上.

图5给出了静态反演方法结果. 可见静态反演得到的各测点处模量波动程度明显大于动态反演结果. 模量窜层现象[8,16,23]导致部分结构层模量被传递到相邻结构层，如2015年，2号和3号测点反演得到的土基模量结果大于800 MPa，而底基层(水稳砂砾)的反演模量小于100 MPa，反演结果不能客观描述土基和底基层的材料特性. 部分测点处2015年的反演结果反而大于2010年的反演结果，服役期间车辆荷载会造成路面材料进一步压实，然而7号测点处的面层模量增长了70%以上，反演结果不能正确地描述筑路材料在服役期间的性能变化.

图4 半刚性基层路面结构动态反演结果Fig.4 Dynamic backcalculated results for pavement with semi-rigid base

图5 半刚性基层路面结构静态反演结果Fig.5 Static backcalculated results for pavement with semi-rigid base

3.2 柔性基层路面结构

对于柔性基层沥青路面结构，动态反演方法将沥青面层和沥青处治基层均作为黏弹性材料，其余结构层作为弹性材料，同理计算沥青层的当量回弹模量，取面层的荷载频率为10 Hz，基层的荷载频率为5 Hz，分析温度均为20 ℃. 图6中绘出了柔性基层路面结构的动态反演结果.

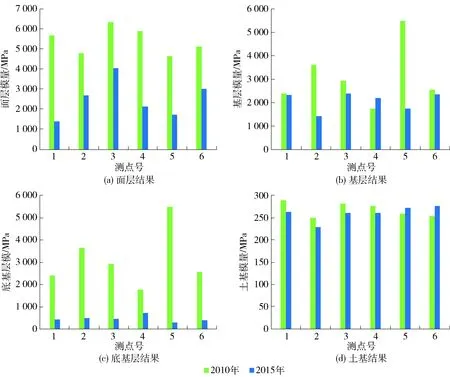
图6 柔性基层路面结构动态反演结果Fig.6 Dynamic backcalculated results for pavement with flexible base

由图可知，各结构层力学参数的动态反演结果均在筑路材料的合理范围内. 5号和6号测点处的土基模量反而有一定的增长，增长幅度小于10%，而底基层的模量衰减程度较大，这一现象是由于底基层强度的衰减，土基承受更多的荷载压力导致的.

图7给出了通过静态反演得到的结构层模量随测点的分布结果，可见部分测点处基层和土基的静态反演结果超出了材料力学参数的合理范围. 2号测点处面层和6号测点处基层的2015年的反演结果远大于2010年的结果，结果显示筑路材料的强度没有减小，反而有了大幅度的增长，静态反演结果无法解释路面结构服役性能的降低.

为更清晰分析各结构层的模量衰减情况， 计算了2个路面结构不同测点的反演结果的平均衰减比，计算公式为

(4)

式中：R为模量衰减比；N为同一路段结构的测点数；E2010,i和E2015,i分别表示第i个测点的2010年和2015年的反演结果.其中：正值表示2015年反演结果小于2010年反演结果；负值表示2015年反演结果大于2010年反演结果.计算结果列于表3中.

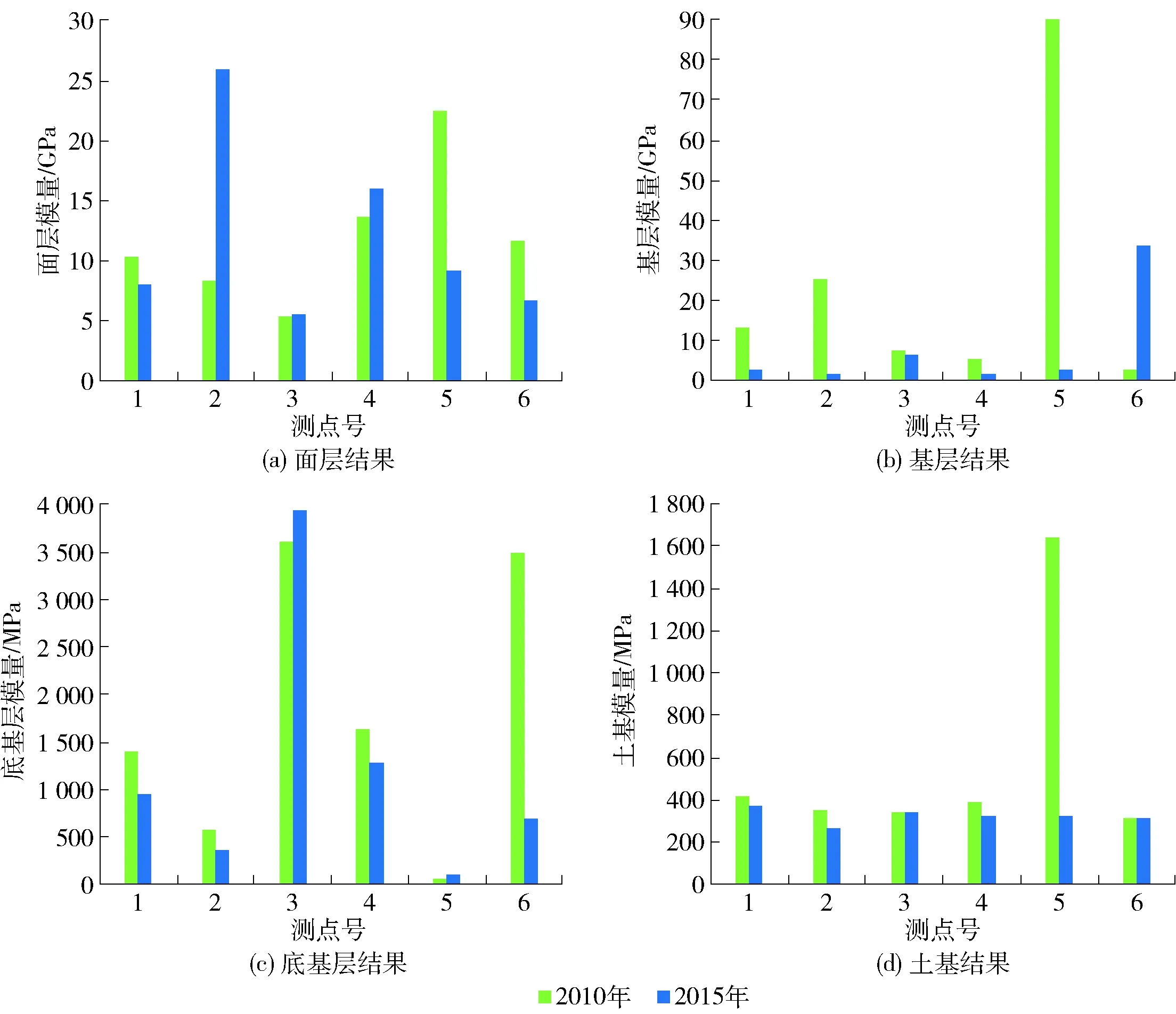
图7 柔性基层路面结构静态反演结果Fig.7 Static backcalculated results for pavement with flexible base

可见，各结构层模量的动态反演结果表现出不同程度的衰减，而静态反演结果中，部分结构层的模量反而有所提升，尤其是柔性基层的反演结果增大了1.2倍以上，这一现象不能客观地描述路面结构承载能力的衰变. 针对半刚性基层路面结构，面层、基层和底基层的模量衰减比相近，表明各结构层强度衰减程度较一致. 对于柔性基层沥青路面，底基层的模量衰减比达到了76.1，明显大于面层和基层的反演结果，底基层模量的衰减将导致沥青基层产生更大的荷载应力，这将进一步导致沥青层疲劳裂缝的发生. 2个路面结构中，土基模量衰减比均小于其他结构层，表明土基在服役期间的强度衰减程度较小. 由上可知，动态方法在路面力学参数反演和结构性能衰减分析方面明显优于静态反演方法.

4 基于动态反演结果的路面力学分析

为进一步验证动态反演结果的合理性，采用2010年和2015年动态反演力学参数进行路面分析，研究路面结构力学响应的变化. 通过动态反演得到沥青层的黏弹力学参数，因此，分析方法采用层状黏弹性理论，荷载采用移动荷载，移动速度选取我国高速公路设计速度的下限值，即80 km/h，具体计算流程可见文献[24]. 在分析过程中，采用整个路段的反演结果平均值作为沥青层的黏弹性参数以及其余结构层的弹性模量. 分析荷载采用单轴单轮荷载，荷载半径为0.15 m，荷载幅值为0.7 MPa. 对于半刚性基层路面结构，计算了沥青层层中竖向应变和底基层层底水平应力；对于柔性基层路面结构，计算了沥青层层中竖向应变和沥青层层底水平应变.

4.1 半刚性基层沥青路面结构

图8绘出了半刚性底基层层底的水平纵向应力结果. 其中：正值表示受拉；负值表示受压；竖线表示荷载作用于分析点正上方时刻. 可见荷载移动过程中，分析点处于受压—受拉—受压的交变状态. 采用反演力学参数计算得到的2015年层底水平应变峰值比2010年结果增加了15%左右，表明随着结构层模量的降低，路面结构内部产生了更大的应力结果，这将导致路面结构服役能力的进一步衰减.

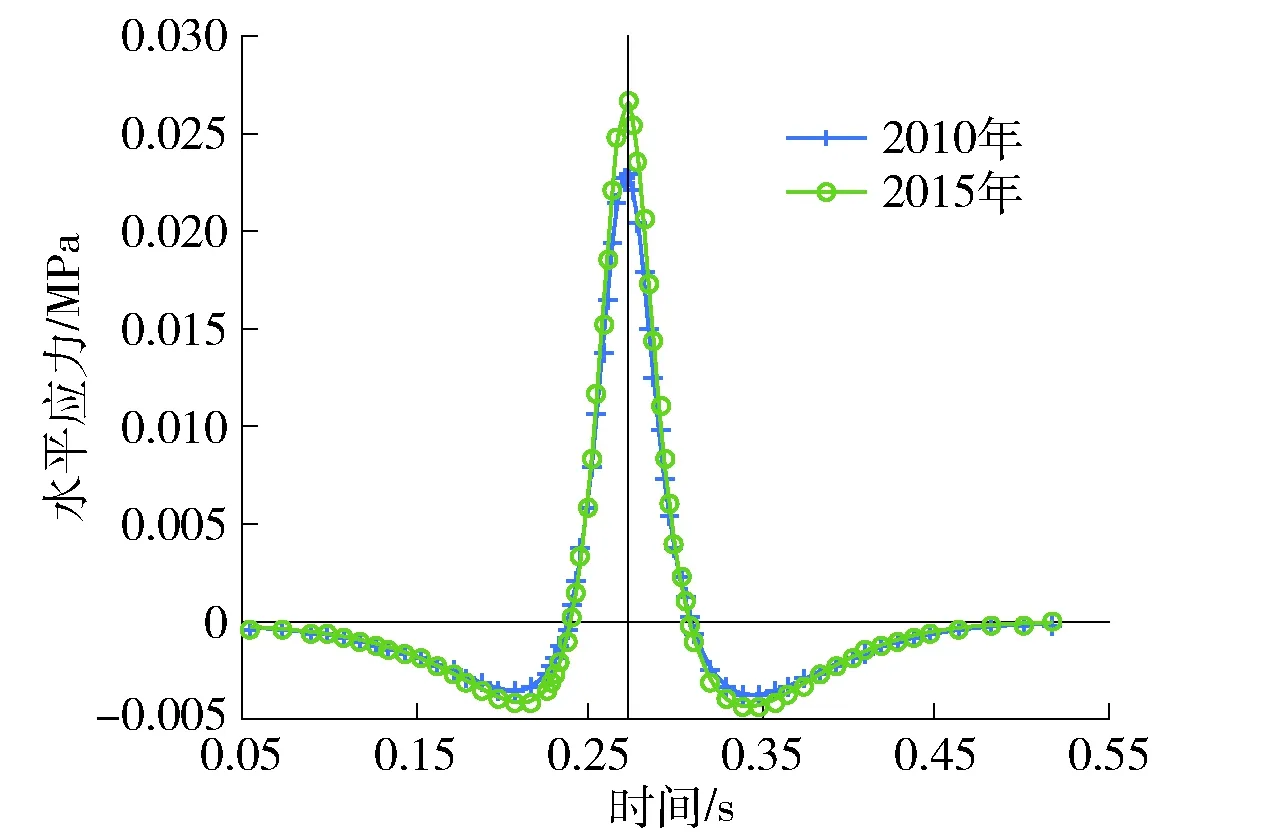
图8 底基层层底水平应力Fig.8 Horizontal stress at the bottom of subbase

图9 绘出了沥青层层中竖向应变的分析结果. 可见，沥青层层中竖向应变峰值增加了80%左右，而且在荷载驶离分析点之后，2015年分析结果的尾部大于2010年的结果，表明2015年产生了较大的永久变形，需要更长的时间恢复变形，分析结果能够描述路面车辙的发展变化[25-26].

4.2 柔性基层沥青路面结构

图10中绘出了柔性基层路面面层和基层层中竖向应变分析结果. 与半刚性基层路面结构相似，计算得到的2015年竖向应变峰值均有所增加，而且产生的永久变形大于2010年的分析结果. 基层和面层层中竖向应变的峰值均增大了70%以上，而且基层分析结果尾部的永久变形大于面层分析结果，表明底基层模量的衰减导致基层和面层产生更大的应力响应，而且基层将产生更大的永久变形.

图9 沥青层层中竖向应变Fig.9 Vertical strain at the mid-depth of asphalt layer

图10 沥青层层中竖向应变Fig.10 Vertical strain at the mid-depth of asphalt layer

图11中绘出了沥青层层底水平应变的分析结果. 可见2015年的分析结果明显大于2010年分析结果，峰值的增加程度大于竖向应变结果，表明结构层强度衰减程度不同，将导致结构内部力学响应重分布.

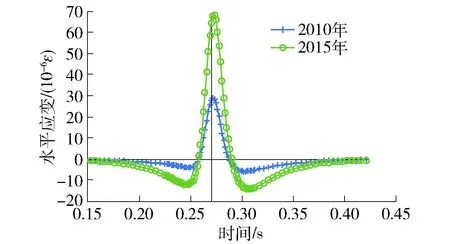
图11 沥青层层底水平应变Fig.11 Horizontal strain at the bottom of asphalt layer

为进一步分析不同结构层模量衰减对路面结构内部力学响应的影响，计算了分析得到的2015年和2010年力学响应峰值的比值(见表4)，可见不同位置处的力学响应峰值有不同程度的增加，表明结构层强度的衰减程度不同，导致路面结构内部产生的荷载应力空间分布特性发生改变. 对于半刚性基层路面结构，沥青层竖向应变的比值大于基层层底水平应力结果. 由表3可知，在分析服役时间内，基层的力学参数衰减程度较低，则在路面结构承载能力中，基层将会承担更多的荷载应力，以保护底基层不至于产生较大的响应. 对于柔性基层路面结构，沥青层层底水平应变峰值比值为2.36，明显大于沥青层层中分析结果，而且基层应变比值大于面层分析结果，可见随着底基层模量的衰减，将导致面层和基层承受较大的荷载应力，尤其是基层层底的水平应变. 采用动态反演结果分析得到路面力学响应结果的变化，与路面力学参数的衰减变化具有高度的一致性，进一步验证了采用动态方法反演路面力学参数，进行路面结构性能衰减分析的可行性.

表4 2010年和2015年力学响应峰值比值

5 结论

1) 采用动态反演方法可以得到沥青层的复数模量主曲线，可以在较宽的频率内描述材料性能，比单一的弹性模量值能更全面描述沥青混合料的温度、荷载频率依赖性.

2) 动态反演得到同一路段不同测点处的结果稳定性高于静态反演结果，动态反演结果可以较好地描述路面力学参数在服役期间的衰减.

3) 分析结果表明，土基层的强度衰减程度明显小于其他结构层结果. 柔性基层路面结构底基层的弹性模量衰减可达70%以上，底基层的衰减导致沥青层承担更大的荷载应力，将会导致路面病害的进一步发展.

4) 利用动态反演力学参数分析得到的路面力学响应的增长趋势和反演力学参数的衰减具有高度的一致性，验证了采用动态反演方法进行路面性能衰减分析的可行性. 研究结论有待于在更多的路面结构类型中进行论证，并考虑不同维养措施的影响，进一步提升路面结构性能衰减的分析精度.