基于新型混合智能算法的图像分割方法

刘俊梅， 马永刚

（榆林学院数学与统计学院，陕西榆林 719000）

图像分割是指将图像分成若干互不重叠的子区域，使得同一个子区域内的特征具有一定相似性、不同子区域间特征呈现较为明显的差异. 图像分割是图像识别、场景解析、对象检测等任务的预处理，是图像进一步分析的基础，是计算机视觉中一项重要技术，其主要任务是准确地分离目标和背景，为后期图像识别和计算机视觉图像处理提供参考.

在国内外众多的分割算法中，阈值分割技术简单有效、易于理解，难点是如何快速有效地搜索最优阈值，准确地分割目标区域和背景区域. 为了进一步提高计算速度和效率，近年来国内外许多学者将智能算法和最大熵阈值分割方法相结合，如多混沌人工蜂群和杜鹃搜索的最大二维熵图像分割算法［1］、改进PSO算法在二维最佳阈值图像分割中的应用［2］、基于二维最大熵原理和改进GA 算法的图像阈值分割［3］、基于改进DE算法的二维最大熵图像分割［4］，但整体效果仍有待提升.

本文将基本DE算法进行了改进，融入多混沌系统和动态调整策略，并将改进后的混沌动态DE算法用于搜索最优阈值，给出一种新的基于混合智能算法的图像阈值分割方法（IHIAIS），并与文献［2］等优化算法进行了比较，进一步验证了本文算法的性能.

1 最大二维熵图像分割法

最大二维熵图像分割法［5-7］以信息熵作为测度，利用图像像素灰度值分布和领域平均灰度值分布构建相应的二维直方图，然后计算最优阈值，尽量最大化图像中目标与背景分布的信息量，由于区域灰度信息对噪声的敏感程度低于点灰度信息，对于低信噪比的图像，采用最大二维熵的图像分割方法会取得较好的效果.

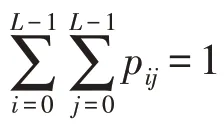
取灰度级L=256，图1表示某一图像二维灰度直方图在二维灰度平面投影图，一般情况下，如果图像的背景区域和目标区域内部比较均匀，二维直方图内(i,j)的概率分布在对角线附近较为集中，整体上呈现双峰状，边界点、噪声点的概率值偏离对角线.

图1 二维灰度直方图平面投影图Fig.1 Plane projection of two-dimensional gray histogram

假设阈值向量(s,t)将二维直方图划分为四个区域A,B,C,D，其中A和B两个区域分别表示目标区域和背景区域，s,t∈{0 ,1,…,L-1}，则：

目标区域A的概率

背景区域B的概率

其中：A={(i,j)|i=s+1,s+2,…,L-1;j=t+1,t+2,…,L-1} ，B={(i,j)|i=0,1,…,s;j=0,1,…,t} ，若远离对角线部分的影响被忽略，则这里可以得到w0+w1=1.

至此，得到B和A的概率分布，分别为：

在施工过程中，建设各方积极深入各个治理区域的治理方案和治理施工管理，各个治理区域施工完成之后进行分单元、分区域验收，在治理结束后，根据永久监测资料和试验检测资料所反馈的信息，对整个自然边坡的治理效果进行验收评价。

则B和A的区域熵分别为：

根据最大熵原理，有

H(s*,t*)=max{H(s,t)} .

最大二维熵图像阈值分割方法中最优阈值的选择本身就是一个优化问题，获得最优阈值［8-9］存在参数多、计算量大、搜索范围广、计算速度慢等问题，这些方面有待进一步提高.

2 基本差分进化算法［10］

其中：rand()表示[0,1]内均匀分布的随机数；CR 为交叉概率因子，范围在[0,1]之间，以上交叉操作能保证xT至少要从xm中获得一个坐标，否则新的向量就不会产生，种群就不会发生变化.

DE算法在选择操作中采用精英式保留策略，将试验个体xT与目标个体xti进行竞争，只有当xT的适应值优于的适应值，xT才被选作子代，否则直接将作为子代.

3 基于新型混合智能算法的图像分割方法

3.1 改进差分进化算法

在初始阶段，引入混沌运动系统，混沌就是由某一状态得到的具有随机性的运动状态，基本混沌系统［11］可以用以下公式来描述：

式中：μ=3.99；(1)=0.597 000,2)=0.597 001，混沌初始化以后，将表示向上取整.

将基本DE算法传统变异方案进行更新，其操作方程［9］为：

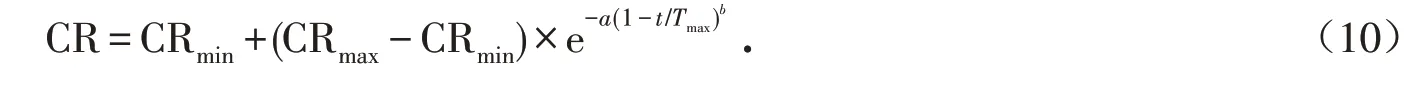
为了提高基本DE算法的优化性能，交叉概率采用指数递增方式，其更新状态如下［9］：式中：a=30；CRmin=0.1，CRmax=0.9；t为当前迭代次数；Tmax为算法最大迭代次数. 该动态CR 能很好地平衡局部搜索、全局搜索能力，使算法快速收敛.

基本DE算法中比例因子F是控制种群收敛性和多样性的重要参数，它决定偏差向量的放大比，如果F的取值过大或者过小，都会有缺陷，本文选取文献［4］中的自适应比例因子，更新状态如下：

式中：Fmin=0.2，Fmax=1.8；t∈[1,Tmax-1]，t为当前迭代次数，Tmax为算法最大迭代次数. 比例因子F根据迭代次数进行调整，迭代初期F取值相对较大，可以保持种群的多样性；在迭代后期，F的值减小，可以保留种群的良好信息，使算法快速收敛.

3.2 新型混合智能算法基本思想

本文对基本DE算法进行改进，加入初始化多混沌系统、新的变异方案、交叉概率的动态调整和比例因子，提高了算法的搜索性能.采用改进的动态DE 算法寻求全局最优阈值，对最大二维熵阈值进行优化，实现高效的图像分割.

该算法的基本思想：通过算法遍历搜索图像灰度空间，来得到目标函数式（5）的最优值，根据最优阈值进行图像分割.

1）计算原始图像二维直方图.

2）在搜索空间进行种群初始化，设置相应参数.

3）根据改进DE算法进行变异、交叉、选择操作，不断更新记录.

4）直到达到终止条件，得到最优阈值，从而获得最大熵值对应的像素点灰度和像素区域灰度均值二元数组(s*,t*).

5）将(s*,t*)作为图像分割的最优阈值，最后进行图像分割.

算法流程图如图2所示.

图2 算法流程图Fig.2 Algorithm flowchart

4 实验结果及分析［12-16］

为了验证本文给出的改进DE算法在最大二维熵图像分割中的效果，实验中选取灰度级为256的lena图像，设置DE算法的搜索空间为256×256，DE算法中向量维数D=2，其中个体的两个分量分别表示像素点灰度和像素区域灰度均值，取值范围为[0,255]. 按照lena图像二维直方图，设置种群大小N=20，最大迭代次数Tmax=50，并将本文改进后的DE算法与文献［1-4］中的算法进行比较. 图3为lena图像的二维灰度直方图，图4（a）为原始lena图，图4（b）、图4（c）分别为本文算法和文献［2］两种算法对lena图像的分割结果图，与文献［2］中的阈值分割方法相比，本文改进DE算法能够更好地分割图像.

图3 lena图像二维灰度直方图Fig.3 Two-dimensional grayscale histogram of lena image

图4 lena图像及不同算法分割结果Fig.4 Lena image and segmentation results of different algorithms

图5是两种算法的熵值迭代变化示意图，可以看出，本文给出的算法利用改进多混沌动态DE算法的优点，能够更好地逼近最优阈值，在收敛速度和收敛精度方面具有明显的优势.

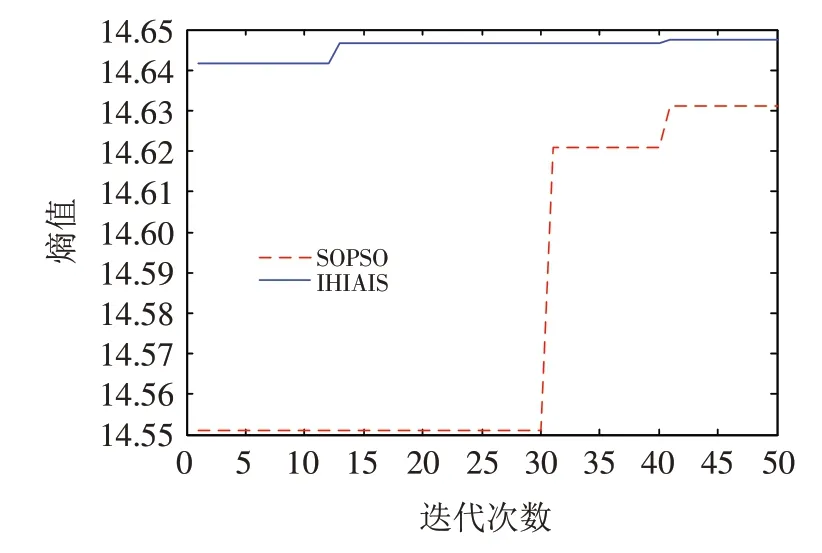
图5 本文算法熵值随迭代次数变化结果Fig.5 The entropy changes of the algorithm in this paper with the number of iterations

为了更好地评价算法，本文选择lena 图像，将改进GA 算法［3］、PSO 算法［2］、人工蜂群优化算法［1］、改进DE 算法［4］、本文算法5种优化算法进行最大二维熵图像分割实验对比，各种算法的基本参数如表1所示，每种算法分别实验20次算法停止，得到最优阈值、最大熵平均值和运行时间平均值，结果见表2.

由表1 和表2 可以看出，在算法结果基本相似的情况下，本文算法的种群规模、迭代次数都比其他四种算法要小得多，在运行时间方面，该算法优于改进GA 算法和ABC 算法，但略低于SOPSO和改进的DE算法. 本文算法通过添加多混沌系统、改变变异策略、并根据迭代次数动态调整交叉概率和比例因子，很大程度提升了计算最佳阈值的效率，降低了计算量并提高了计算速度.

表1 五种优化算法基本参数设置Tab.1 Basic parameter settings of five optimization algorithms

表2 五种优化算法实验结果对比Tab.2 Comparison of experimental results of five optimization algorithms

5 结语

本文将多混沌动态DE 算法和最大二维熵图像分割方法相结合进行图像分割，充分发挥了两种算法的优势. 实验结果表明，该算法比常用的图像分割方法具有更好的图像分割效果和收敛速度效果，在搜索最优阈值时有具有更好的鲁棒性和收敛性.