自适应高斯变异花授粉算法

李文超， 贺兴时， 贺飞跃， 杨新社

（1.西安工程大学理学院，西安 710048； 2.密德萨斯大学科学与技术学院，英国伦敦 NM4 4BT）

人类在研究领域和工程领域面临众多亟待解决的优化问题. 传统优化算法在解决这些问题时，求解精度和收敛速度等方面均不能满足实际需求且耗时、耗力. 因此，学者们开发了大量的自然启发式优化算法，如粒子群优化算法（Particle Swarm Optimization，PSO）［1］、象群游牧算法（Elephant Herding Optimization）［2］等.

最近，英国学者Yang［3］受自然界植物花朵授粉过程的启发提出了一种新颖的元启发式算法——花授粉算法（Flower Pollination Algorithm，FPA）. 基于FPA的实现简单、参数少、易调节等优点，FPA已广泛用于函数优化［4］、移动机器人路径规划［5］、车间调度［6］等领域. 然而与其他仿生优化算法类似，基本FPA也存在收敛精度低、速度慢、维数敏感等问题［7］. 为此，国内外学者针对基本花授粉优化算法进行诸多研究，主要体现在以下3个方面：①初始种群的改进. 由于群智能优化算法的初始种群为以后进化过程提供了初始猜想，所以初始种群质量的好坏影响了算法收敛速度和收敛精度等. 基本FPA算法采用随机的方式对种群进行初始化，导致种群分布不均，算法容易早熟. 针对这种缺陷，张水平和高栋［8］利用霍尔顿序列生成更加均匀的初始种群；宁杰琼和何庆［9］认为Logistic 混沌映射可以使种群分布更加均匀. ②转换概率的改进. 转换概率可以调整FPA算法中全局搜索和局部搜索之间平衡［10］；Valenzuela等［11］利用模糊推理系统动态调整转换概率，有助于算法跳出局部最优；Liu等［12］将韦伯分布函数与迭代次数结合用于控制转换概率，有助于全局搜索和局部搜索之间平衡；田海梅和徐胜超［13］根据迭代次数和步长因子调整转换概率. ③搜索策略的改进. 汪海等［14］为了使搜索方向不断靠近最优值，引入时滞调整算子；陆克中等［15］采用量子搜索机制，将个体吸引到可能出现的任意位置，个体的随机性增强了算法的全局搜索能力；肖辉辉等［16］提出将惯性权重的三角变异机制和精英变异融合组成新的局部搜索机制.

虽然花授粉有一定的改进，如收敛速度明显加快，解的精度明显提高，但是在精度和维数敏感问题方面仍有提升空间. 本文引入佳点集初始化种群的方法，解决种群分布不均的问题；然后，提出一种根据迭代次数和振荡函数调整转化概率的策略；最后分析了基本花授粉算法中的自花授粉公式的搜索能力，提出用高斯变异自花授粉公式引导算法精细搜索. 实验结果表明新算法的改进策略有效.

1 基本花授粉算法

在自然界中，花朵授粉过程纷繁复杂. 如果过多地考虑花朵授粉的各个细节，就会导致计算资源的浪费且实用价值不大. 为了使算法简单易行，该算法做如下理想化假设：

1）生物异花授粉是带花粉的传播者通过Levy飞行进行全局授粉的过程；

2）生物自花授粉是一个局部授粉过程；

3）花的常性可以被认为是繁殖概率和参与的两朵花的相似性成比例关系；

4）转换概率p0∈[0,1]控制着全局授粉和局部授粉之间的转换.

异花授粉过程定义如下：

其中：X、分别表示第t+1代、第t代的解；g*为全局最优解；L为步长，L服从Levy 分布，即

其中：λ=1.5；Γ(λ)为标准的伽马函数；s为移动步长.

自花授粉模拟自然界中同种花之间近距离接触，授粉过程定义如下：

其中：α∈[0,1]服从均匀分布；、为同种植物的不同花朵的花粉.

2 自适应高斯变异花授粉算法（AGFPA）

2.1 基于佳点集理论的种群初始化

FPA从随机初始化花粉配子开始寻优，若存在一些在最优解附近的花粉配子，则能够提高算法的收敛和寻优能力，反之则很难或者无法找到最优解. 因此，通过初始化均匀的种群，才能使实际问题得到更好的解决. 华罗庚和王元［17］提出了佳点集理论，其定义如下：

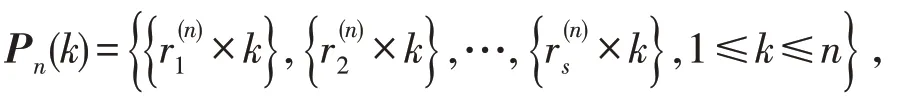
本文通过引入佳点集理论，创建初始化种群公式，公式如下：

其中：Xi表示第i个花粉配子的位置；ub，lb分别表示解的上界和下界.

图1是分别采用随机方法和佳点集方法生成规模为50的二维初始化种群分布图. 由图可知，在相同点数下，佳点集产生的点比随机产生的点更加均匀.

图1 初始化种群Fig.1 Initial population

2.2 自适应调整的转化概率

根据文献［10］可知，在迭代前期FPA 算法偏重于异花授粉，在迭代后期算法偏重于自花授粉. 当转换概率p0为固定值时，不利于自花授粉与异花授粉之间的平衡. 针对该问题，文献［18］提出了IFPA算法，该算法将固定概率p0增强为动态概率p1，公式如下：

其中：p1_min为最小概率；p1_max为最大概率；t为当前迭代次数.

由图2可知，IFPA算法的动态概率p1在200次迭代左右，由于p1较小，花粉配子侧重于自花授粉过程，导致该算法在解空间中搜索不充分，易陷入局部最优. 为此，定义动态转化概率pa如下：

图2 IFPA算法概率p1 曲线分布Fig.2 Curve distribution of probability p1 of IFPA algorithm

其中：τ ∈[0 ,1] 服从均匀分布的随机数；t、Niter分别表示当前迭代次数、最大迭代次数；pa_min、pa_max分别表示pa的最小值和最大值. 根据文献［3］提供的参数可知，当转换概率为0.8 时，FPA 算法的性能较高；根据文献［19］可知，当转换概率为0.2时，算法性能较高. 经过深入分析后，设置pa_min为0.2，设置pa_max为0.8. 由图3可知，当it∈[0,600]时，pa取值较大，AGFPA算法偏重于全局搜索，使得该算法可以对解空间进行充分搜索.当it∈[600,1000]时，pa取值相对较小，AGFPA算法偏重于局部搜索，使得该算法在解空间中进行精细搜索.

图3 AGFPA算法概率pa 曲线分布Fig.3 Curve distribution of probability pa of AGFPA algorithm

2.3 高斯变异自花授粉机制

在FPA 算法中，自花授粉更新公式采用随机的搜索方式进行局部开发. 当算法进入后期时，种群差异较小(-g*≈0)，导致个体很难找到更优的位置，因此削弱了算法精细搜索的能力. 因此，将高斯变异算子作为自花授粉更新公式，不仅增加种群多样性，而且提高了算法续航能力. 同时高斯变异能以较大的概率产生较小的变异值，使得其在小范围内不易陷入局部最优. 高斯变异自花授粉公式如下：

其中：X，分别表示第t+1 代、第t代的解；ε∈[0 ,1] 服从均匀分布，N(0,1)服从标准正态分布. 式（7）表

示在原有花粉配子运动的基础上，加入正态分布扰动项，有利于跳出局部最优解.

2.4 自适应高斯变异花授粉算法

为了提高花授粉算法的寻优精度和稳定性，克服该算法易陷入局部最优的缺陷，利用佳点集理论初始化的种群，通过自适应转化概率调整自花授粉与异花授粉，提出自适应高斯变异花授粉算法. 算法伪代码如下：

①初始化参数，设定花粉种群规模N、最大迭代次Niter、转换概率最大值pa_max和最小值pa_min；

②利用佳点集初始化花粉的位置，并计算适应度值；

③记录当前的全局适应度最小值和最优解；

④依据式（6）计算转换概率pa；

⑤若条件（rand＜pa）成立，转步骤⑥；否则，转步骤⑦；

⑥全局授粉：根据式（1）更新子代花粉位置，并计算适应度值；

⑦局部授粉：根据式（7）更新子代花粉位置，并计算适应度值；

⑧计算全局适应度最小值，并更新最优解；

⑨若满足终止条件，输出全局最优解；否则，转至步骤④.

3 实验仿真与结果分析

3.1 实验设计

为了检验算法的性能，选择11个标准的测试算法，其中包括多峰非旋转高维函数f1～f5、单峰多维函数f6～f10和2维多峰函数f11. 函数的具体描述如表1所示.

表1 测试函数Tab.1 Test function

续表

3.2 测试环境和算法参数

实验环境如下：CPU 为i7-10750H 2.60 GHz，运行内存8 GB，操作系统Windows10，编程环境Matlab R2021a. 所有的测试函数维数为10、50和100，种群规模为25，最大迭代次数Niter=1000 . 算法参数设置如表2.

表2 算法参数设置Tab.2 Algorithm parameter setting

3.3 算法求解精度比较分析

AGFPA、IFPA、FPA、EHO、PSO对11个测试函数的实验结果如表3～13. 其中，std为解的标准差、best为最优解、mean为解的平均值、worst为最差解.

表3 f1(x) Ackley函数仿真结果Tab.3 Simulation results of f1(x)Ackley function

表4 f2(x) Rastrigin函数仿真结果Tab.4 Simulation results of f2(x)Rastrigin function

表5 f3(x) Griewank函数仿真结果Tab.5 Simulation results of f3(x)Griewank function

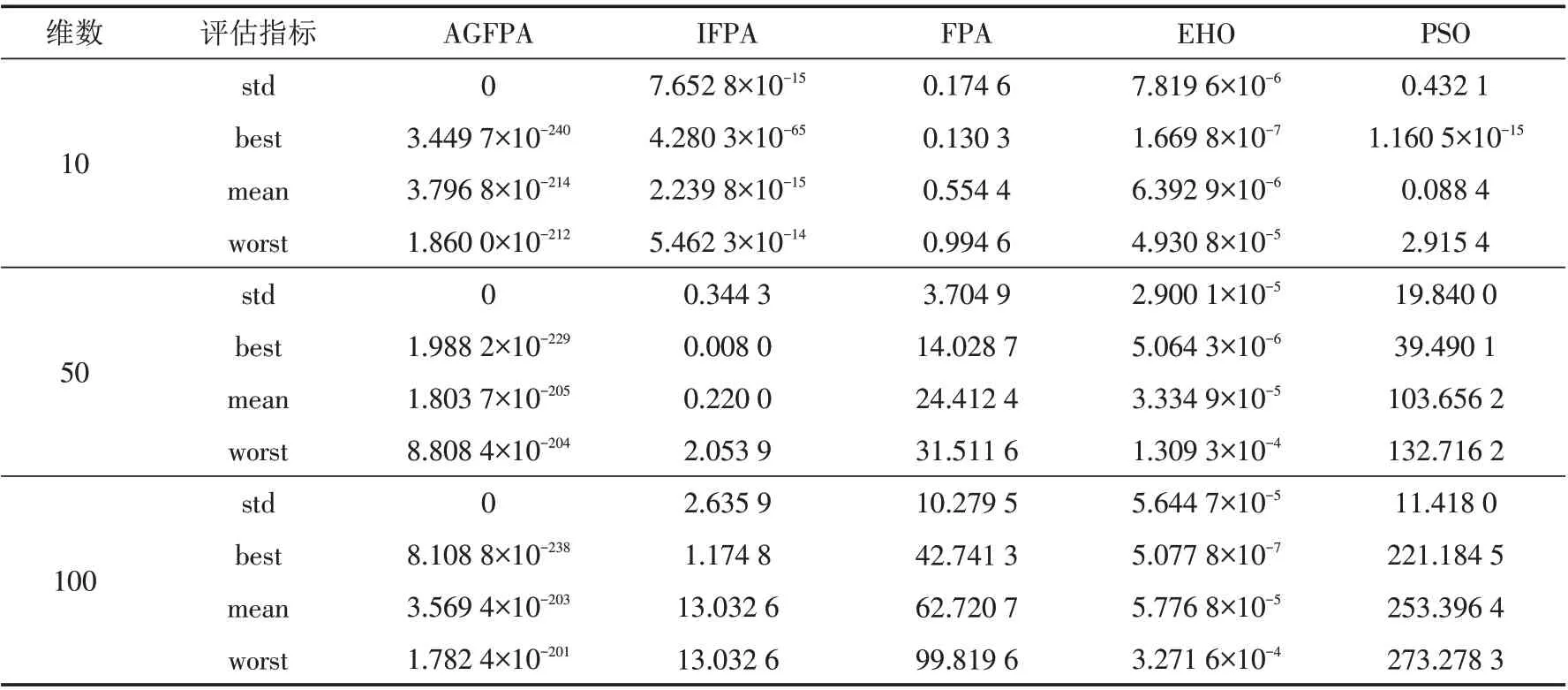
表6 f4(x) Alpine函数仿真结果Tab.6 Simulation results of f4(x)Alpine function

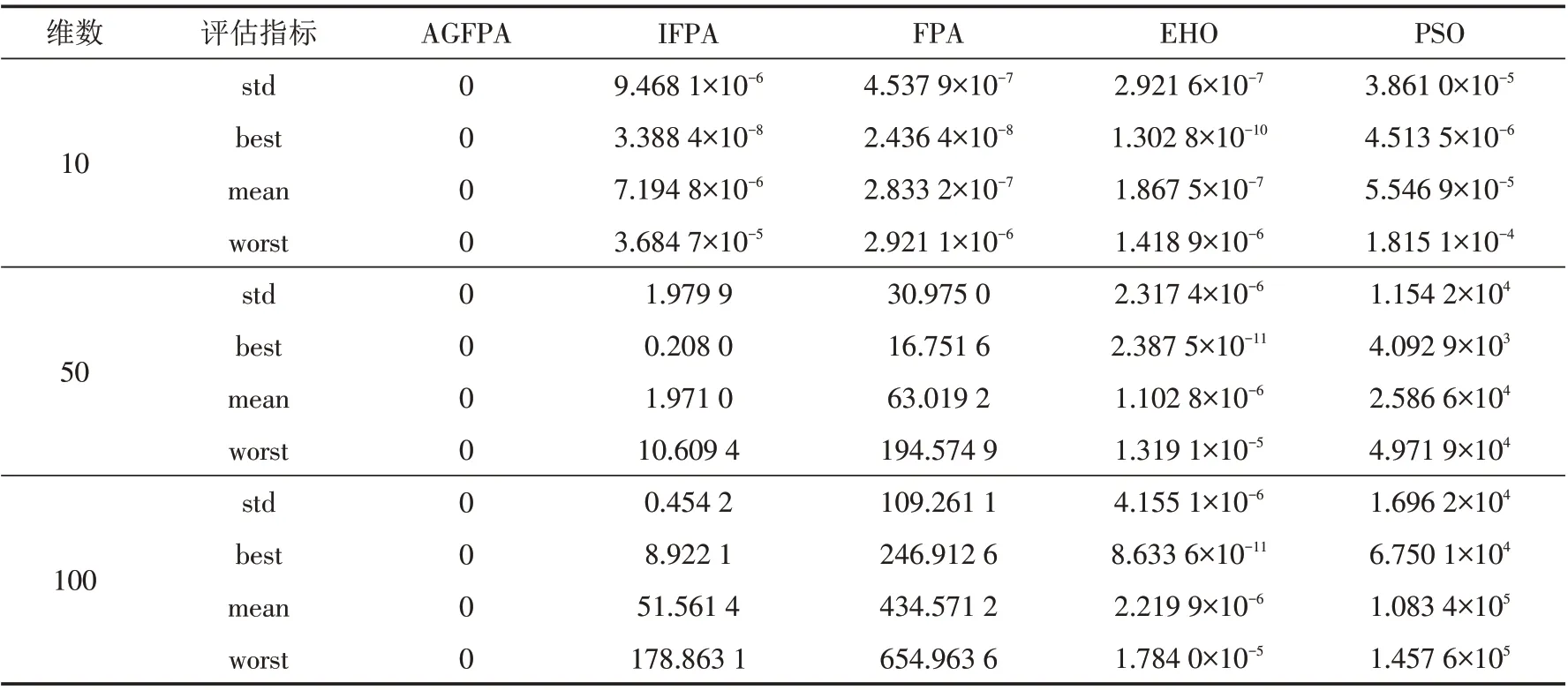
表7 f5(x) Powell函数仿真结果Tab.7 Simulation results of f5(x)Powell function

表8 f6(x) Rotated Hyper-Ellipsoid函数仿真结果Tab.8 Simulation results of f6(x)Rotated Hyper-Ellipsoid function

表9 f7(x) Sphere函数仿真结果Tab.9 Simulation results of f7(x)Sphere function

表10 f8(x) Sum of Different Power函数仿真结果Tab.10 Simulation results of f8(x)Sum of Different Power function

表11 f9(x) Sum square 函数仿真结果Tab.11 Simulation results of f9(x)Sum square function

表12 f10(x) Zakharov函数仿真结果Tab.12 Simulation results of f10(x)Zakharov function

表13 f11(x) Schaffer函数仿真结果Tab.13 Simulation results of f11(x)Schaffer function

最优解和平均值可以反映算法的收敛精度和搜索能力. 通过表3～7的结果对比分析可得，IFPA、FPA、EHO 和PSO在求解高维非旋转多模态函数的时候，均陷入局部最优，难以跳出局部最优，导致优化效果差.而改进的AGFPA算法，引入佳点集理论初始化种群，并使用振荡的自适应概率控制局部搜索和全局搜索的平衡，用高斯变异自花授粉公式替换随机搜索公式，使算法的收敛精度大大提高. 特别是f2、f3和f5均达到理论值. 通过表8～12对比分析可得，AGFPA算法在高维单峰函数上均搜索到理论最优值，而其他四种算法没有获取到理论最优值，这说明AGFPA算法具有较强的搜索单峰函数的能力. 基于维度的增加，IFPA、FPA求解精度变差，这说明算法对维数比较敏感. 通过表13分析可得，AGFPA、IFPA、FPA、EHO和PSO算法均可以解决低维函数优化问题.

算法的标准差和最差解反映算法的鲁棒性和跳出局部最优的能力. 与其他算法相比，AGFPA 算法在11个标准测试函数的标准差最小，这说明算法比较健壮.

3.4 算法收敛分析

为了更加直观地分析AGFPA算法的性能，上述11个测试函数的收敛曲线图如图4～14所示.

图4 Ackley函数收敛曲线Fig.4 Convergence curves of Ackley function

图5 Rastrigin函数收敛曲线Fig.5 Convergence curves of Rastrigin function

图6 Griewank函数收敛曲线Fig.6 Convergence curves of Griewank function

图7 Alpine函数收敛曲线Fig.7 Convergence curves of Alpine function

图8 Powell函数收敛曲线Fig.8 Convergence curves of Powell function

图9 Rotated Hyper-Ellipsoid函数收敛曲线Fig.9 Convergence curves of Rotated Hyper-Ellipsoid function

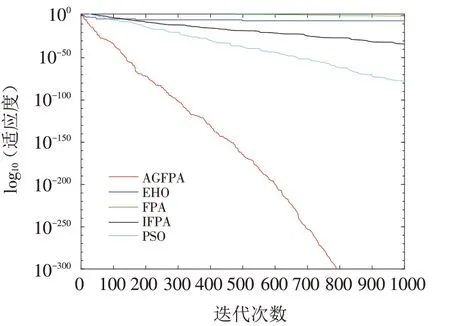
图10 Sphere函数收敛曲线Fig.10 Convergence curves of Sphere function

图11 Sum of Difference Power函数收敛曲线Fig.11 Convergence curves of Sum of Difference Power function

图12 Sum square函数收敛曲线Fig.12 Convergence curves of Sum square function

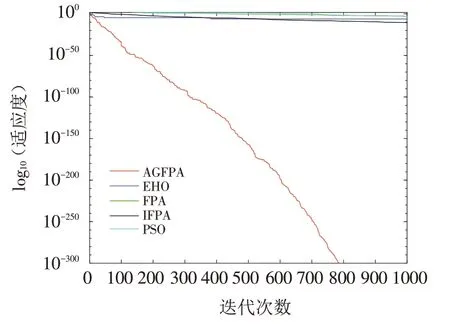
图13 Zakharov函数收敛曲线Fig.13 Convergence curves of Zakharov function

图14 Schaffer 函数收敛曲线Fig.14 Convergence curves of Schaffer function

在图中，横坐标为算法的迭代次数t，纵坐标为算法的适应度值的对数. 从图的曲线可以看出，FPA算法的收敛速度比较慢，收敛精度一般. 改进的AGFPA 算法不但有较快的收敛速度，而且有较好的收敛精度.除了f1和f4没有搜索到理论最优解，其他函数均搜索到理论解，这说明算法具有较强的搜索能力. 从图4可以看出，算法后期仍有不断下降的趋势，这说明AGFPA算法仍具有持续优化的能力，避免类似FPA算法及其他算法存在的早熟现象.

3.5 时间复杂度比较

使用策略的时间复杂度来衡量AGFPA、IFPA和FPA算法的时间复杂度，时间复杂度结果如表14所示.

表14 时间复杂度结果Tab.14 Time complexity results

由表14可知，无论从初始化策略来看，还是从转换概率更新策略或者授粉过程策略来看，AGFPA、IFPA和FPA算法之间的时间复杂度不存在差异. 通过分析可知，AGFPA算法没有增加算法难度，进而表明算法的可行性.

3.6 统计检验

Wilcoxon检验是一种非参数检验，用于判断AGFPA算法与其他算法是否有显著性差异. Wilcoxon检验假设H0：AGFPA算法性能和另外一种算法性能相同；H1：AGFPA算法性能优于另外一种算法性能. 其结果显示在表15中，其中，P表示检验结果、S表示显著性判断结果. 当P＜0.05 时，S显示为“+”，表示当P>0.05时，AGFPA 算法优于另外一种算法；S 显示为“-”，AGFPA 算法与另外一种算法无差异. 当P显示维“NaN”时，S显示为“～”，表示无法进行显著性判断.

表15 Wilcoxon检验结果Tab.15 Wilcoxon test results

取每种算法在10个10维测试函数和1个2维函数上独立运行30次的平均值进行秩和检验，从表15可以看出，AGFPA算法与FPA算法在函数f2、f6和f11上无法进行显著性判断；AGFPA算法与IFPA算法在函数f11无法显著性判断；AGFPA算法与PSO算法在函数f11无法显著性判断；在函数AGFPA算法在函数f4上弱于PSO算法. 对于其他函数P值均远远小于0.05且S均显示为“+”. 说明AGFPA算法比IFPA、FPA、EHO和PSO更有显著优势.

4 结语

针对基本花授粉算法在求解函数优化问题时，存在收敛速度慢，精度低和维度敏感等问题，本文提出了自适应高斯变异花授粉算法. 该算法为增加种群多样性，引入佳点集理论；为了增加自花授粉和异化授粉之间转换的灵活性，构建了振荡的自适应概率pa；为了避免在后期类似其他算法出现的早熟现象，构建了高斯变异自花授粉公式. 通过对11 个测试函数的仿真，并与IFPA、FPA、EHO 和PSO 对比分析，AGFPA 在求解低、高维函数优化问题时，具有较好的收敛精度、较快的收敛速度和健壮的鲁棒性. 下一步将研究AGFPA算法在约束优化问题中的应用，使其具有更大潜能.