空间变异液化夹层位置对盾构隧道地震响应影响规律研究

娄建高， 许 昊， 张 弛， 慈 伟

（1.中铁隧道集团三处有限公司，广东深圳 518052； 2.西南交通大学交通隧道教育部重点实验室，成都 610031）

21世纪以来，随着城市化进程的加快，地铁在城市交通系统中发挥着越来越重要的作用. 在大规模的地铁修建过程中，某些城市的地铁隧道不可避免地会存在液化夹层［1-2］. 起初人们认为隧道等地下结构的破坏小于地面结构，不需要进行抗震设计，但后来有学者［3-5］发现，地震发生时会伴随着隧道破坏现象，并且大部分隧道破坏是由地震液化引起的. 迄今已有较多关于液化夹层中隧道的抗震研究. Zheng等［6］利用FLAC（Fast Lagrangian Analysis of Continua）软件建立了多元自适应回归模型，并分析了位于饱和砂土中的圆形隧道的变形规律，为评估隧道的上浮位移提供了简洁高效的方法. Bao等［7］采用基于土-水完全耦合的有限元-有限差分方法研究了液化夹层中大型矩形地铁隧道的抗震性能，并对隧道产生上浮位移的机理进行了分析. Azadi和Hosseini［8］对土体发生液化时的超静孔隙水压力的变化进行了监测，分析了土体参数和上覆土层对隧道上浮量的影响. 郑刚等［9］在充分考虑孔隙水与土之间耦合作用的基础上分析了地下结构在地震过程中的超静孔隙水压力变化、加速度反应、上浮位移以及结构周围土体的变形规律.

综合来看，目前关于地下结构地震响应的研究大多是将土体视为均质材料，但是实际工程中的岩土体参数具有空间变异性，即不同空间位置处的土体物理力学参数并不相同［10-11］，因此将土体视为均质材料进行研究是不符合实际情况的. 为了解决上述问题，有些学者［12-15］开始采用随机场模型来描述土体参数的空间变异性. Vanmarck［16］首次提出采用齐次正态随机场、变异系数、相关函数来描述土体参数的空间变异性. 易顺等［17］基于随机场理论研究了土体刚度参数对基坑开挖引起的变形规律的影响，发现变异系数和波动距离的增大会使变形分布更加分散. 刘辉等［18］在考虑抗剪强度空间变异性的基础上提出了黏土边坡失效概率计算方法. 由于土体剪切模量会对结构地震响应有显著影响［19］，且以往的研究尚未分析液化夹层中土体剪切模量的空间变异性对隧道的影响，因此本研究在考虑土体剪切模量空间变异性的基础上，基于随机场理论，利用FLAC3D软件建立了液化夹层与盾构隧道的数值模型，并分析了不同液化夹层位置下的隧道地震响应规律.

1 基于随机场理论的盾构隧道地震响应分析

随机场理论的实质是用平稳正态随机场（即高斯平稳齐次随机过程）来模拟土体参数剖面的变异性［20］.随机场的模拟方法有很多，本研究用二维对数正态分布来模拟土体剪切模量（G）的变异性，其中二维对数正态分布随机场可以表示为：

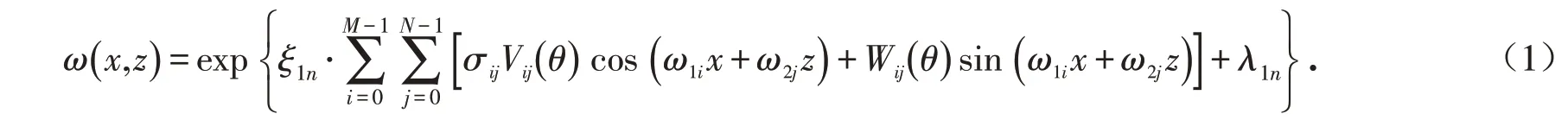
式中：λ1n和ξ1n分别为对数场（即土体剪切模量随机场取对数后的值）的均值和标准差；σij为第iM+j+1 项的标准差；Vij(θ)和Wij(θ)为相互独立的标准正态分布随机变量；ω1i和ω2j为频率坐标值；x和z为空间横向和竖向坐标值.

上述参数中Vij(θ)和Wij(θ)可分别通过土体剪切模量的均值和变异系数来计算，即：

式中：μ和CCOV分别为土体剪切模量的平均值和变异系数.

同时，用指数型自相关函数来表示任意两点间土体剪切模量的相关程度：

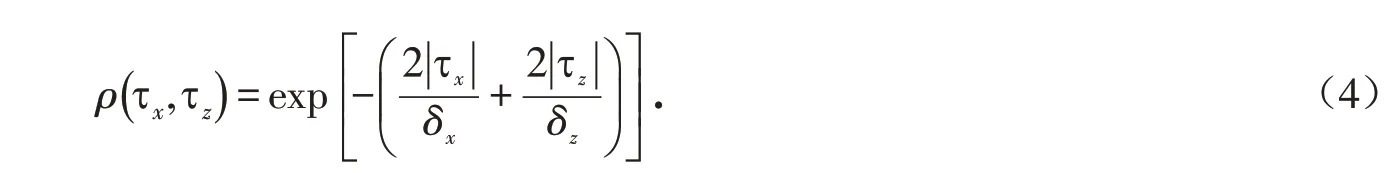
式中：ρ(τx,τz)表示任意两点间土体剪切模量的相关性大小；τx和τz为任意两点土体剪切模量在x、z方向的间距；δx和δz为任意两点土体剪切模量在x、z方向的波动距离. 当δx=δz时，土体剪切模量在空间上表现为各向同性；当δx≠δz时，土体剪切模量在空间上表现为各向异性.

基于随机场理论，本研究对盾构隧道地震响应的分析分为三个步骤：

1）利用FLAC3D软件建立液化夹层与盾构隧道的数值模型.

2）将液化夹层的土体剪切模量设为固定值（G=20 MPa），随后把参数输入到FLAC3D 软件中进行计算，得到的结果即为一次确定性计算结果，并与之后的随机性计算结果进行对比分析.

3）基于随机场理论，用二维对数正态分布来模拟液化夹层土体剪切模量（G）的变异性. 在随机场理论中，CCOV和δ分别对土体参数的空间变异性和相关性有影响［21］. 本研究中设置CCOV=0.2，δx=δz=10 m，共设置50组液化夹层的土体剪切模量. 不同液化夹层位置下的一组土体剪切模量随机场云图如图1所示. 然后将50组液化夹层的土体剪切模量输入到FLAC3D软件中进行计算，即可得到隧道地震响应的数据（即为随机性计算结果）.

图1 液化夹层土体剪切模量随机场云图Fig.1 Random field cloud diagram of shear modulus of liquefaction interlayer soil

2 数值模型的构建及材料参数的选取

2.1 数值模型的构建

利用FLAC3D有限差分软件建立液化夹层与盾构隧道的数值模型，数值模型宽50 m，高30 m，隧道埋深10 m，隧道直径6 m，衬砌厚度0.3 m，地下水位线位于地表处，如图2所示. 模型中选用的地基土体为黏土，其中含有厚度为6 m的砂土液化夹层，设置的液化夹层的位置共有三种：在隧道上方、环绕在隧道周围、在隧道下方，这三种位置对应的中心埋深H分别为3、10、17 m.

图2 液化夹层与盾构隧道的数值模型Fig.2 Numerical model of liquefaction interlayer and shield tunnel

2.2 材料特性与参数

FLAC3D软件中有空模型、弹性模型和塑性模型三种，空模型通常用来表示被移除或被开挖的材料，故本研究采用空模型模拟隧道的开挖部分. 隧道衬砌为混凝土材料，可采用各向同性的弹性模型进行模拟. 塑性模型中常用摩尔-库仑模型来模拟岩土体，因为利用摩尔-库仑模型进行计算可以获得土体在剪切作用失稳时的力学响应，并且模型的设置参数少、计算效率高.

地基土体采用实体单元模拟. 考虑到隧道与土的相互作用，采用shell结构单元模拟衬砌结构［22］. 由于数值模型的地下水位线位于地表处，即地基土体处于完全饱和状态，因此需考虑渗流作用. 地基土体和隧道衬砌结构的物理力学参数及其取值分别如表1和表2所示.

表1 地基土体的物理力学参数及其取值Tab.1 Physical and mechanical parameters and their values of foundation soil

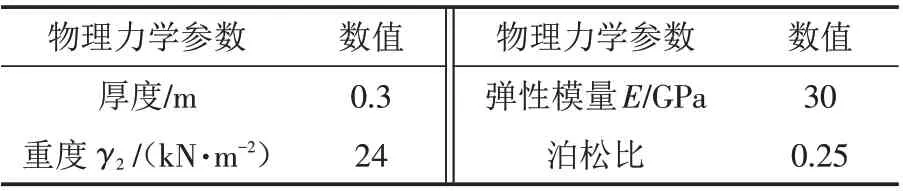
表2 隧道衬砌结构的物理力学参数及其取值Tab.2 Physical and mechanical parameters and their values of tunnel lining structure

因为本研究将液化夹层的土体设置为砂土，所以在进行模拟时需要考虑砂土液化夹层在动力作用下的孔压积累，故本研究采用张建民等［23-25］研究中采用的砂土液化后大变形本构模型来模拟砂土液化夹层，所用参数取值与文献［23］中的参数取值相同.

2.3 动力荷载

本研究以较高的抗震设防烈度为标准，选用的抗震设防烈度为8度，采用对应峰值加速度为0.2 m·s-2的El-Centro 波作为动力荷载，地震波持续时间为30 s，由模型底部节点输入，沿水平方向传播. 地震波加速度时程曲线如图3所示.

图3 地震波加速度时程曲线Fig.3 Time-history curve of seismic wave acceleration

2.4 边界条件

整个计算过程包括静力分析和动力分析两个部分. 在静力分析中，首先进行初始应力平衡，然后开挖隧道内土体，开挖隧道的同时施加衬砌结构，这一过程中模型底部为固定边界条件，限制水平方向和竖直方向的位移；模型两侧仅限制水平方向位移，上表面为自由边界. 在动力分析中，采用自由场边界来减少模型边界上地震波的反射.

3 计算结果与分析

3.1 液化夹层土体超静孔压比分析

超静孔隙水压力是指饱和土体中超出静水压力的孔隙水压力. 地震作用下，液化夹层中的土体趋于密实，土体的超静孔隙水压力急剧上升，增加的超静孔隙水压力与监测点初始有效应力的比值即为超静孔压比. 通过确定性计算和随机性计算得到的不同液化夹层位置下液化夹层土体的超静孔压比如图4 所示，其中监测点水平位置为隧道左侧土体中心. 液化夹层在隧道上方、液化夹层环绕在隧道周围以及液化夹层在隧道下方这三种情况所对应的监测点埋深Z分别为1、8、15 m. 确定性计算时，液化夹层的土体剪切模量为定值（G=20 MPa），因此确定性计算结果只有一个. 在随机性计算中，液化夹层的土体剪切模量并不是固定值，本研究中共设置了50组液化夹层的土体剪切模量，因此随机性计算结果有50个，故在与确定性计算结果作对比分析时，采用的是50个随机性计算结果的均值.

如图4所示，地震荷载作用下，液化夹层的土体超静孔压比首先会出现负值，随后逐渐上升. 随着液化夹层埋深的增加，监测点Z处（深度分别为1、8、15 m）液化夹层的土体超静孔压比逐渐减小，这可能是因为随着液化夹层埋深的增加，土体初始有效应力相应增加. 当液化夹层在隧道上方及液化夹层环绕在隧道周围（Z=1 m和Z=8 m）时，通过随机性计算得出的液化夹层土体超静孔压比均大于通过确定性计算得出的液化夹层土体超静孔压比，这表明在计算液化夹层土体超静孔压比时，若不考虑土体空间变异性，会导致计算得出的结果比实际结果偏低.

图4 不同液化夹层位置下液化夹层土体的超静孔压比的确定性计算值和随机性计算均值的对比Fig.4 Comparison of deterministic calculation values and random calculation mean values of excess static pore pressure ratios of liquefied interlayer soils under different liquefied interlayer locations

3.2 隧道顶点上浮位移分析

地震荷载作用下，液化夹层中的土体超静孔隙水压力急剧上升且在短时间内来不及消散，会使隧道周围地基土体的有效应力和地基承载力降低，最终导致隧道等地下结构会有不同程度的上浮响应. 通过随机性计算和确定性计算得到的不同液化夹层位置下的隧道顶点上浮位移如图5所示.

图5 不同液化夹层位置下通过确定性计算和随机性计算得到的隧道顶点上浮位移Fig.5 Floating displacements of tunnel apexes obtained by deterministic calculation and stochastic calculation under different liquefied interlayer positions

由图5可知，当液化夹层在隧道上方或隧道下方时，隧道顶点上浮位移在地震作用的前5 s内迅速增加，随后略微下降；当液化夹层环绕在隧道周围时，隧道顶点上浮位移在地震作用的前3 s内迅速增加，随后基本保持平稳，之后在地震作用的最后5 s又逐渐增加并达到最大值. 不同液化夹层位置下通过随机性计算得到的隧道顶点上浮位移曲线形状与通过确定性计算得到的隧道顶点上浮位移曲线形状均类似，但其数值在确定性计算结果附近的一定范围内波动. 统计不同液化夹层位置下的隧道顶点最大上浮位移可知，随着液化夹层埋深的增加，通过随机性计算得到的隧道顶点最大上浮位移分别有60%、30%、20%的概率超过通过确定性计算得到的隧道顶点最大上浮位移，这表明在进行隧道顶点上浮位移计算时，若将土体视为均质材料而不考虑土体空间变异性，则有可能导致计算得出的结果比实际结果偏低，从而会导致高估隧道结构的安全性，并且液化夹层埋深越浅，越可能会高估隧道结构的安全性.

由图6可知，当液化夹层在隧道上方及液化夹层环绕在隧道周围时，通过随机性计算得到的隧道顶点上浮位移均值均大于通过确定性计算得到的隧道顶点上浮位移值，这与液化夹层的土体超静孔压比（图4）表现出的规律一致. 当液化夹层环绕在隧道周围时，隧道顶点上浮位移最大，通过确定性计算得到的隧道顶点最大上浮位移值为3.43 cm，通过随机性计算得到的隧道顶点最大上浮位移均值为3.50 cm；当液化夹层在隧道上方时，通过确定性计算得到的隧道顶点最大上浮位移值为2.76 cm，通过随机性计算得到的隧道顶点最大上浮位移均值为2.78 cm；当液化夹层在隧道下方时，通过确定性计算得到的隧道顶点最大上浮位移值为1.06 cm，通过随机性计算得到的隧道顶点最大上浮位移均值为1.08 cm. 由此可见，当液化夹层在隧道下方时，隧道结构在地震作用下的上浮量最小，隧道的安全性最佳；当液化夹层环绕在隧道周围时，隧道的抗震性能最差.

3.3 地表土体竖向位移分析

地下结构的上浮会对隧道周围地基土体产生相互作用，导致地表土体不同位置处发生隆起或沉降等竖向变形. 以隧道中轴线正上方地表土体为对称中心，横向每隔4 m设置一个监测点，然后通过随机性计算和确定性计算分析不同液化夹层位置下地震结束时刻的地表土体竖向位移，结果如图7所示.

从图7可以看出，随着距隧道中轴线距离的增加，地表土体竖向位移逐渐减小，即当距离隧道中轴线较远时，地表土体会发生沉降变形. 隧道的存在弱化了隧道附近地表土体的空间变异性，因此隧道中轴线附近地表土体的竖向位移的确定性计算值和随机性计算均值都很接近，而距离隧道中轴线距离较远时，通过确定性计算和随机性计算得到的地表土体竖向位移相差较大. 当液化夹层位于隧道上方时，远离隧道中轴线的地表土体沉降量较大，甚至超过了隧道中轴线处地表土体的最大隆起位移；当液化夹层环绕在隧道周围时，隧道中轴线处地表土体的隆起值最大，远离隧道中轴线的地表土体的沉降量相对较小；当液化夹层在隧道下方时，隧道附近地表土体的竖向位移相对较小. 结合图4和图6可知，当液化夹层在隧道下方时，液化夹层对隧道和土体的地震响应影响均较小.

图6 不同液化夹层位置下隧道顶点上浮位移的确定性计算值和随机性计算均值的对比Fig.6 Comparison of deterministic calculation values and random calculation mean values of tunnel apex floating displacements under different liquefied interlayer positions

图7 不同液化夹层位置下地震结束时刻的地表土体竖向位移的确定性计算值和随机性计算均值的对比Fig.7 Comparison of deterministic calculation values and random calculation mean values of vertical displacements of the ground surface soils at the end of the earthquake under different liquefied interlayer positions

4 结论

基于随机场理论，在考虑液化夹层土体剪切模量空间变异性的基础上，采用数值模拟方法研究了液化夹层位置对盾构隧道地震响应的影响，所得结论如下：

1）对于存在液化夹层的地基，隧道与液化夹层的相对位置对隧道和土体的地震响应影响较大. 随着液化夹层埋深的增加，液化夹层的土体超静孔压比逐渐减小. 当液化夹层环绕在隧道周围时，地震荷载作用下的隧道顶点上浮位移和地表土体竖向位移均最大，隧道的抗震性能最差；当液化夹层位于隧道下方时，液化夹层的土体超静孔压比、隧道顶点上浮位移及地表土体竖向位移均较小，此时液化夹层的存在对隧道地震响应的影响最小，隧道的安全性最佳.

2）不同液化夹层位置下，通过随机性计算得到的隧道顶点最大上浮位移均大于通过确定性计算得到的隧道顶点最大上浮位移，且液化夹层埋深越浅，通过随机性计算得到的结果越有可能超过通过确定性计算得到的结果，这表明将土体视为均质材料的传统分析方法会高估隧道在地震作用下的安全性. 本研究结论可为液化区隧道的抗震设计提供指导.