变后掠翼柔性复合蒙皮面外弯曲性能建模与验证
蒋华毅,丁江民,肖洪,杨广,王云飞,刘荣强,郭宏伟
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.哈尔滨工业大学 机器人技术与系统国家重点实验室,黑龙江 哈尔滨 150001)
变后掠翼的主要设计思想是在飞行过程中驱动机翼在平面内产生相对转动,使整机前缘与水平线之间的夹角、机翼展弦比能够得到适时调整,如图1所示.它的优势在于可通过后掠角的大范围变化来相应缓解飞行器在高低速状态中的激波阻力和诱导阻力,使其可以同时满足超音速飞行、亚音速巡航以及低速起降时的应用需求,极大地优化了飞行器在多工况条件下的综合使用效率[1].变形蒙皮作为变后掠翼骨架与外界大气间的重要接触媒介,自身必须具备大变形能力.此外,在完整工况条件下,蒙皮还需拥有低的面内刚度来降低驱动器能耗、 高的面外刚度以承受面外
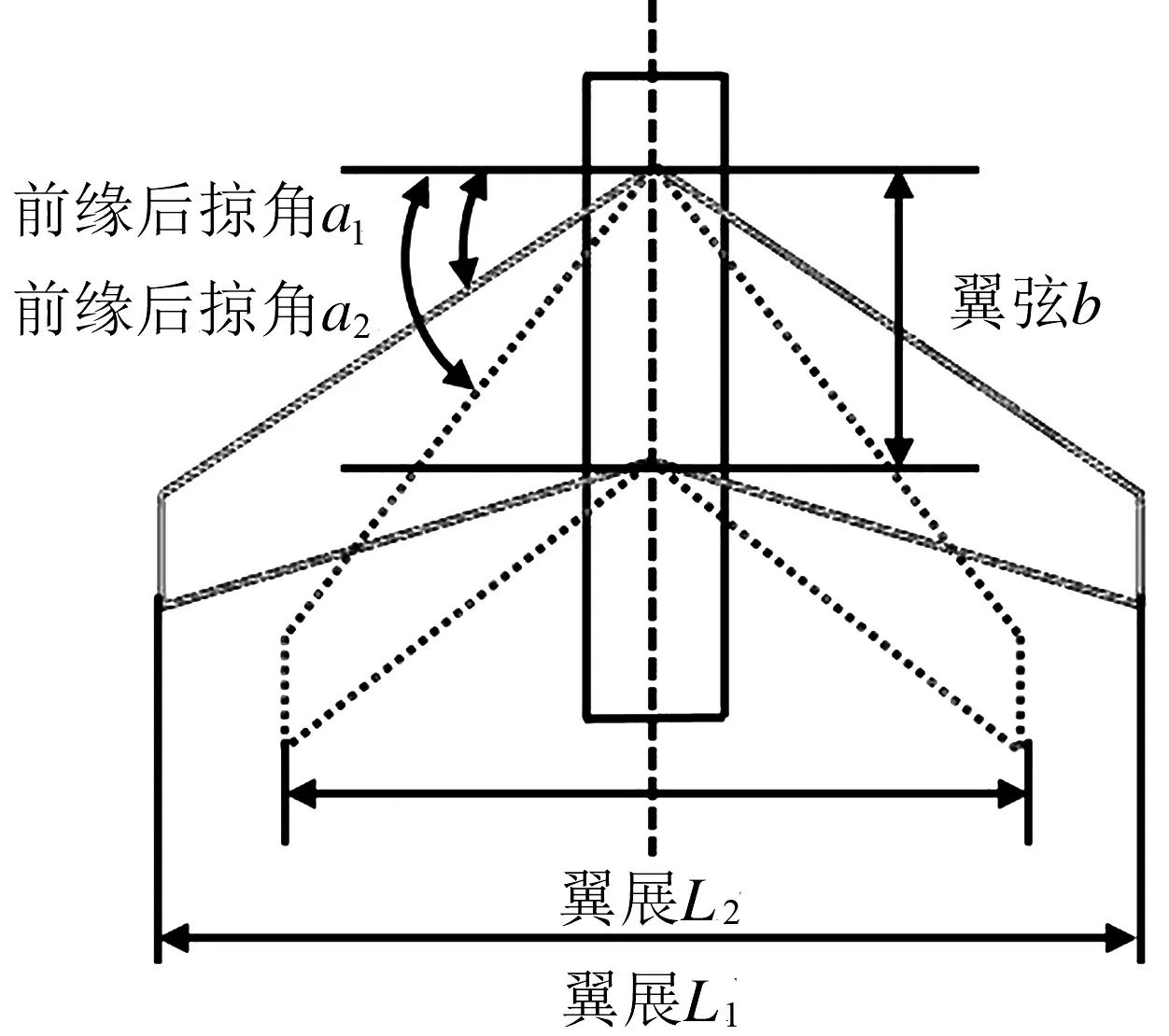
图1 变后掠翼形态变化
气动负载、良好的气密性和表面光滑性去维持气动外形确保综合效率[2].但上述基本设计要求彼此间相互矛盾,为变形蒙皮的研究和设计带来了巨大的困难和挑战.
截至目前,国内外针对变后掠翼蒙皮的研究主要可划分为两大类:第一类是基于内外翼两段式结构的刚性蒙皮,其根据变形形式的差异又可细分为滑动式和旋转式.它的内翼与机身相固定,外翼则通常被设计成多个刚性面,通过驱动机构的作用使外翼围绕固定点产生转动或滑动以实现外形布局的变化[3].然而,内外翼连接区域会遗留台阶和缝隙致使表面光滑性和气密性不足,这将严重影响飞行器的气动效率.第二类是由美国新一代航空公司提出的基于预张紧处理的柔性蒙皮[4],为保证优异的变形量,其表皮材料一般选用超弹性体,可通过施加一定比例的初始预应变来延缓剪切褶皱的产生,但是柔性材料长时间处于张紧状态下会产生蠕变和应力松弛现象,蒙皮整体的结构稳定性能会逐渐丧失.此外,由于超弹性体几乎不具备承载能力,往往需要在其表面粘接自适应结构以提供辅助支撑,从而额外增大了单元重量和驱动能.
由于上述两类蒙皮存在的缺陷显著且解决难度较大,因此本文研究了一种无须预拉伸处理、具备良好承载能力、可实现剪切变形的柔性复合蒙皮.本文综合考虑传统纤维复合材料的基本构型和褶皱幅值的影响因素,开展了蒙皮结构设计.随后,为探究其面外刚度的影响因素以简化设计难度,在连续梁理论的基础上,建立了面外弯曲性能参数化模型.最后,利用有限元仿真分析和静力承载试验的测试方法,从多角度检验了理论模型的合理性.
1 增强型柔性复合蒙皮设计
1.1 蒙皮结构设计
以传统纤维复合材料模型为基础,柔性基体选用具备一定耐温性和延伸率的超弹性硅橡胶以实现低速飞行状态下表面大变形的能力.基体中部等间距平行嵌入了多根支撑梁来提升整体的抗弯刚度,同时可有效解决辅助支撑外部粘接所带来的增重问题.由于硅胶为惰性物,与刚性体嵌合度较差,为防止支撑梁在运动过程中从基体中剥离脱落,造成局部撕裂致使整体性能失效,在梁的上下两侧正交嵌入数根纤维束以限制其纵向滑动,蒙皮结构如图2所示.
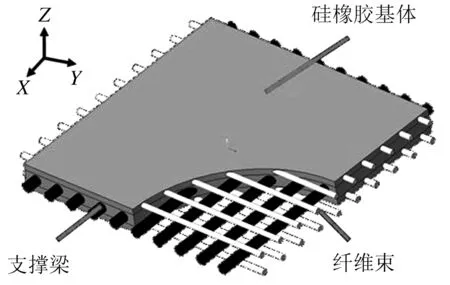
图2 柔性复合蒙皮结构
1.2 蒙皮变形原理
当柔性材料表面张力在局部区域小于0时,此区间范围内极易伴随微小的波动而产生屈曲褶皱.此时,其外形尺寸参数是影响褶皱产生、幅值大小以及周期性排布的主要影响因素[5].从图2可直观看出,柔性基体内部已被支撑梁和纤维束均匀划分成棋盘上网格结构,可等同于柔性复合蒙皮由无数多个微小的代表性体积单元所构成,结构稳定性能够得到大幅度提升.
根据经典层合板理论[6],复合蒙皮整体可近似视作并联三层板.由于支撑梁和纤维束的轴向弹性模量较大,因此,蒙皮在X、Y双向上无法进行均匀拉伸或压缩运动,仅能够实现平面剪切变形.此时,其初始剪切模量仅与各组分材料参数以及所占体积比有关,可通过理论计算对不同布置参数条件下的蒙皮变形难易程度进行预测评估.
2 蒙皮面外承载挠度参数化建模
可变后掠飞行器在飞行状态下,机翼表面会因外界气动载荷的作用而产生纵向挠度位移.此时,如果蒙皮自身面外弯曲刚度不足则会出现较大的凹陷进而降低飞行器的气动性能和综合效率.由于橡胶基体自身几乎没有抗弯刚度,而纤维束截面直径和材料模量又远远低于刚性杆,所以本文假设柔性复合蒙皮的承载性能全部由等间距排布的支撑梁所提供.此时,影响蒙皮纵向挠度的因素主要与内嵌梁的布置间距、直径、长度以及面外载荷有关.
由土木建筑工程中经常使用的连续梁结构可知,在均布荷载作用条件下,于梁的下方添加一定数量的支座可以显著提升结构的承载能力[7].本文以此为基础,并综合考虑在增强蒙皮面外刚度的同时,避免机翼重量过大而增添额外驱动损耗,最终将安装模块设计为铰接日字形结构,如图3所示.
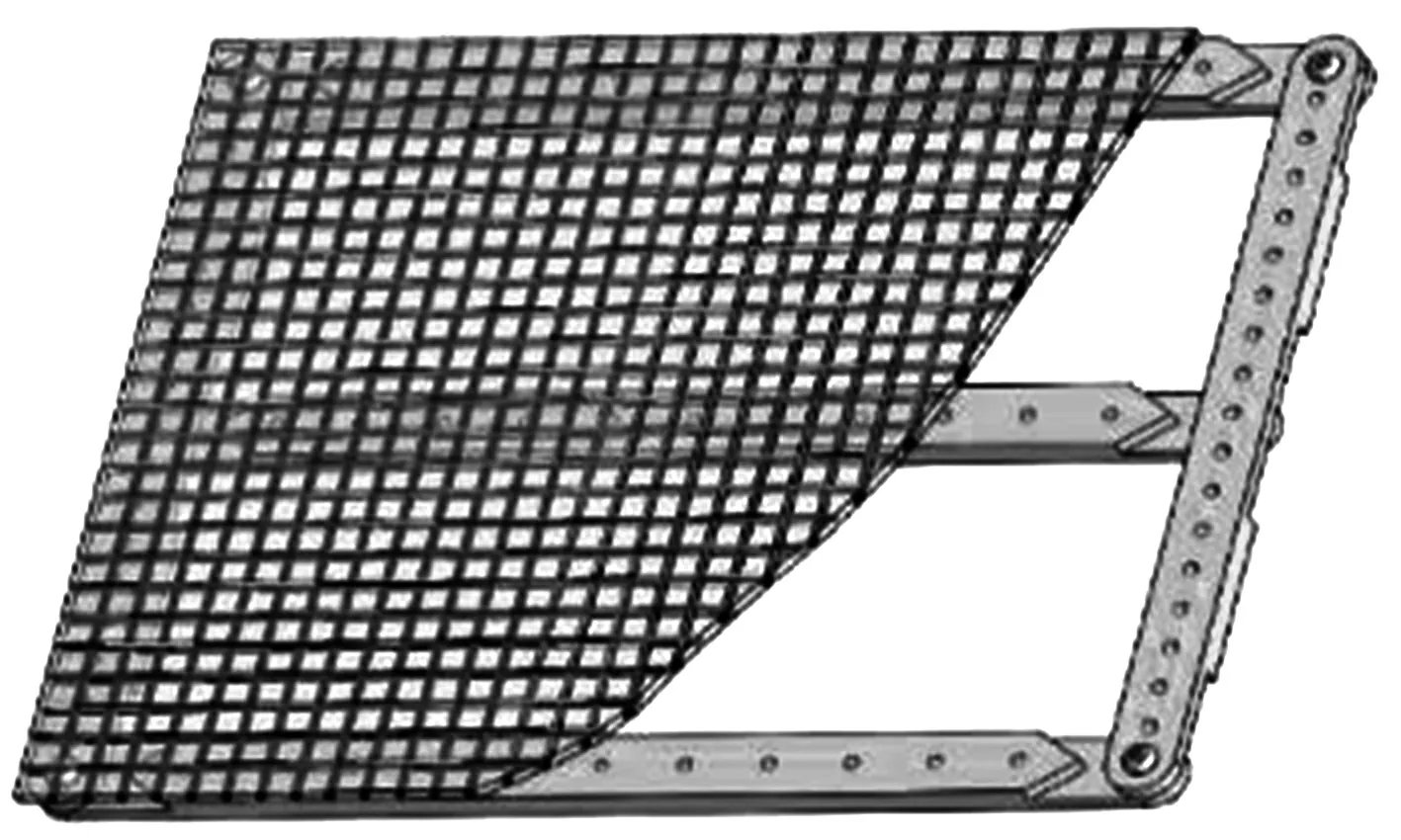
图3 蒙皮承载安装单元
此时可将蒙皮内嵌杆视作二跨连续梁结构,其在均匀线载荷下的挠度位移为:
Z=Kql4/100EI
(1)
式中:查参考文献[7]中表3-2可得二跨梁中点挠度系数K为0.521;q为梁所受均布线载荷,N/mm2;l为梁的跨内轴向长度,l=0.5 L梁,mm;E为梁的轴向弹性模量,MPa;I为梁的截面惯矩,mm4.
内嵌支撑梁截面为圆形,其截面惯矩I定义为:
I=πd梁4/64
(2)
蒙皮基体表面在均匀压强条件下,内嵌梁所受到的线载荷可通过下式求解:
q=PS梁
(3)
式中:P为压强,MPa;S梁为支撑梁排布间距,mm.
联立式(1)、式(2)、式(3)可推导出纵向挠度位移U与梁布置间距S梁、梁截面直径d梁和梁轴向长度L梁的关系式为:
(4)
3 蒙皮承载挠度仿真分析
为验证蒙皮面外弯曲理论模型的准确性,使用有限元软件ABAQUS对柔性复合蒙皮的承载挠度进行了数值分析.模型整体为3D全尺寸模型,外形尺寸为230 mm×310 mm×(d梁+1)mm.由于硅橡胶基体材料需内嵌增强体,所以采用了C3D8RH单元来模拟其力学行为.内嵌支撑梁的建模应用了B32单元,并通过线性阵列的方式平行排布在橡胶基体中间层区域.为节省建模时间和计算成本,同时保证有限元模拟的收敛性和准确性,以加强筋模型为基础[8],应用SFM3D4单元中的rebar层来对芳纶纤维束的材料属性、间距、截面直径及铺设角度进行设定并对称布置于梁的上下两侧.在装配体界面,将各组成体网格节点一一合并进而实现了柔性复合蒙皮数值模型的建立,如图4所示.
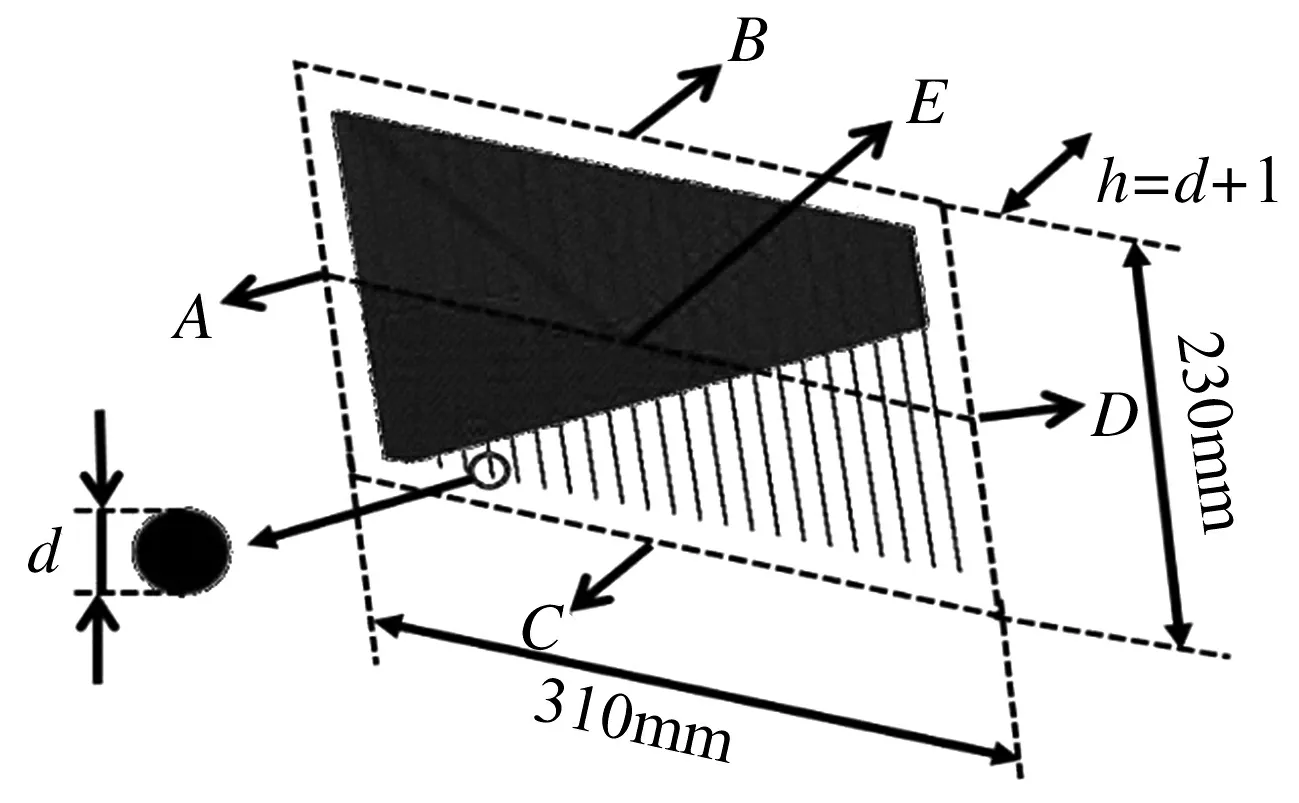
图4 柔性复合蒙皮数值模型
有限元模型各单元材料属性如表1所示,其中,C10和C01为硅橡胶本构材料参数.按照表2中所列的位移约束边界以及工况条件对有限元模型进行了相应设置,得到了多组承载仿真数据.其中,梁截面直径为2 mm、排布间距为4 mm的蒙皮承载挠度分布如图5所示.从中可以看出,在辅助支撑的约束下,蒙皮整体的纵向承载挠度具有对称性,其变形最大值出现于安装模块空隙内的中心区域.
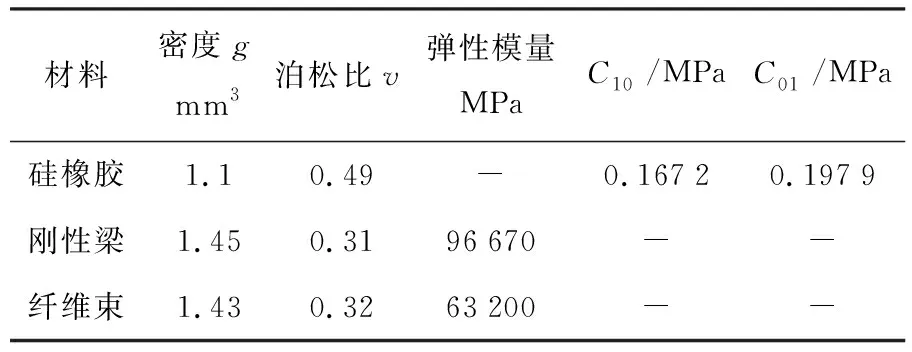
表1 材料属性
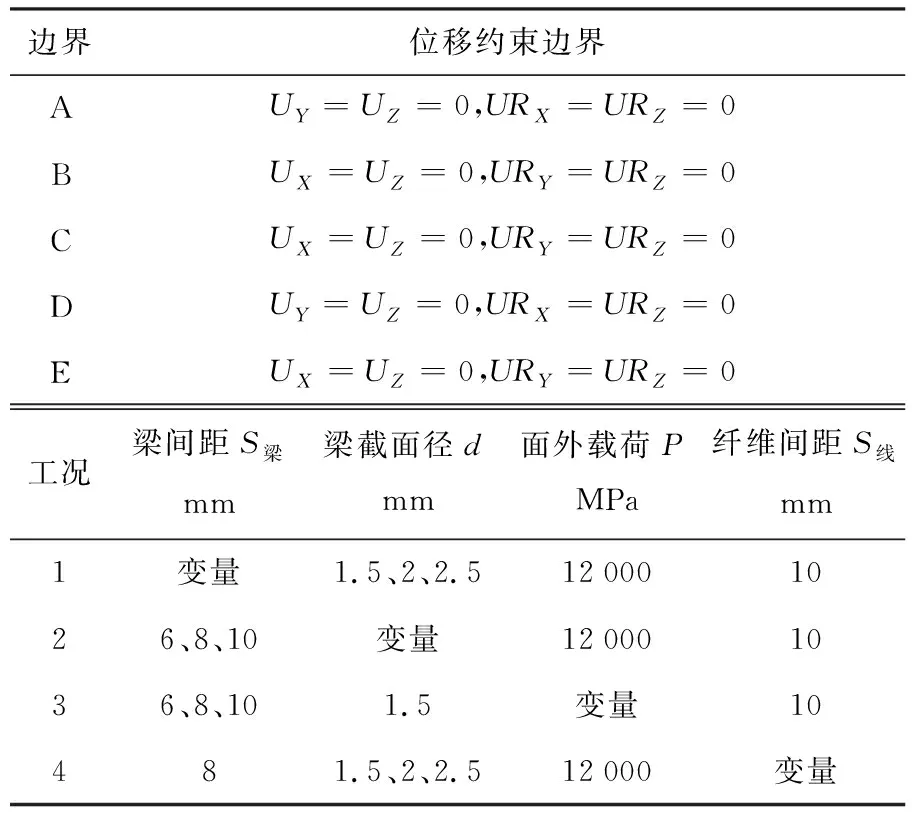
表2 数值模型边界及工况条件

图5 承载仿真云图
进一步对不同工况条件下的仿真数据和理论结果进行统计处理和对比分析,并分别汇总于图6.结果显示,蒙皮挠度仿真值与各参数变量理论曲线吻合程度高,变化趋势一致,有效验证了蒙皮面外弯曲理论模型的可靠性和有限元模型的准确性.从曲线变化趋势方面进行考虑,蒙皮的纵向承载挠度与纤维束数量基本呈水平关系,与梁布置间距以及面外均布载荷呈良好的正比例关系,而与梁截面直径呈高阶非线性关系,直接说明了梁截面参数影响蒙皮面外刚度的主要因素.
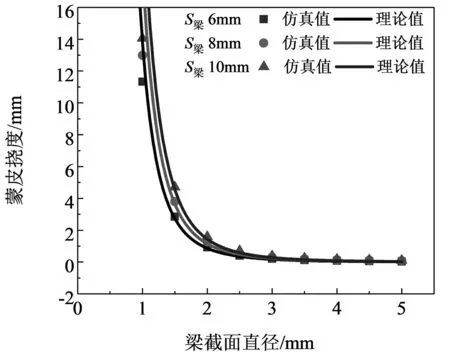
(b)梁截面直径-承载挠度关系
4 试验验证
考虑到样件制作以及实验测试的成本及复杂程度,在保证样件外形尺寸与仿真模型一致的条件下,本文仅针对蒙皮厚度约为2.2 mm,d梁为1 mm,S线为3mm,S梁分别为3、6、9 mm的柔性复合蒙皮进行了承载力学测试.如图7所示,试验系统由实验台、安装模块单元、蒙皮样件、亚克力承载箱、激光测距仪以及数据采集装置所构成.测试过程中,首先在承载水箱内侧包裹一层透明方底袋并保证袋底可与蒙皮表面紧密贴合.随后,向袋中多次注入质量相等的水以等效代替样件面外所受到的均布载荷.依据承载仿真云图,将激光测距仪布置于安装模块单个空隙的中心区域,并实时记录测试点的纵向挠度数据以供后处理,实验结果如图8所示.

图7 蒙皮承载测试系统
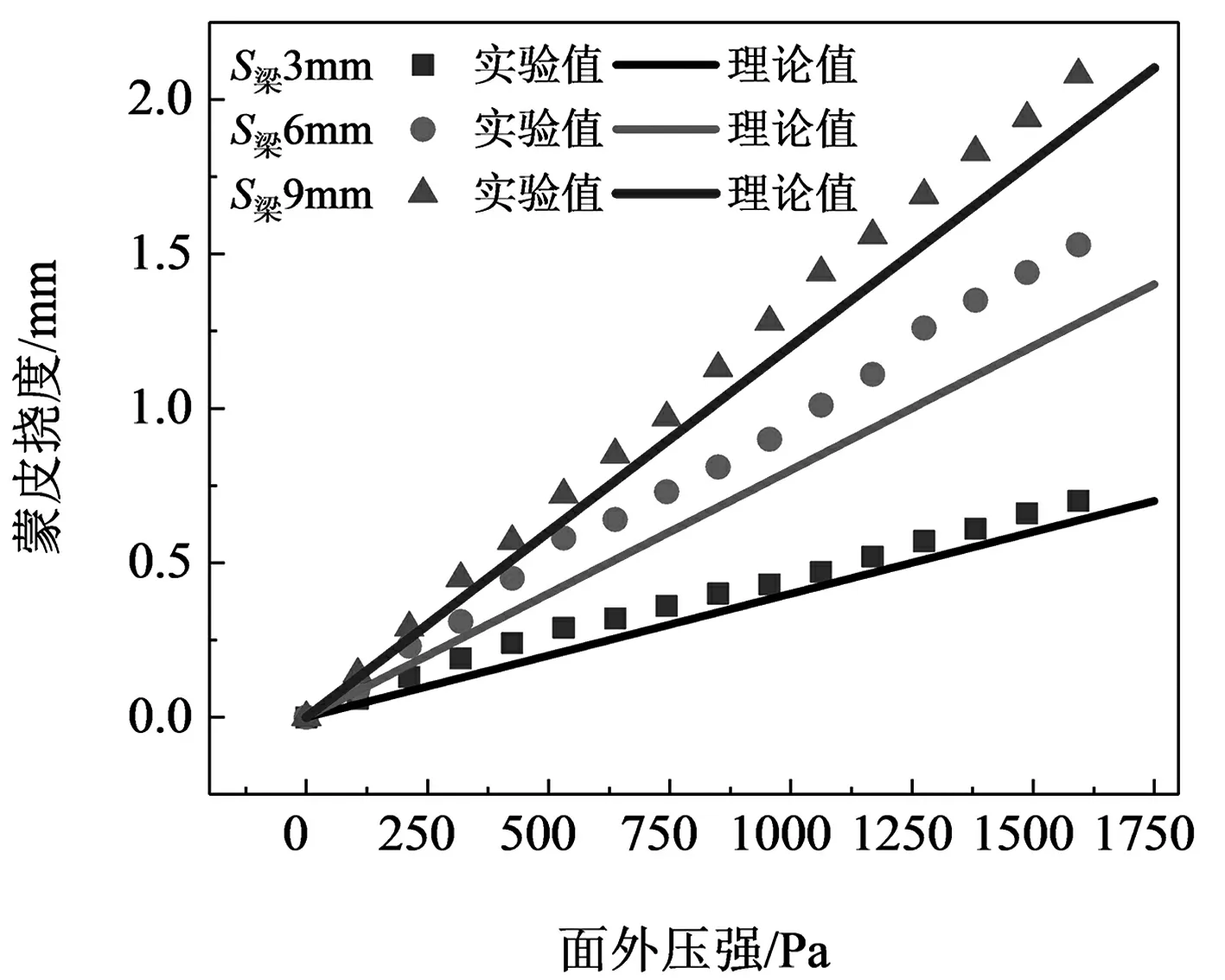
图8 蒙皮变支撑梁间距承载数据曲线
由于复合蒙皮的参数化模型是以梁变形特性为基础进而提出的,而在实际测试时柔性基体会于梁之间的空隙处产生额外凹陷,并且各工况下的固定边界难以保证完全一致,致使数值仿真结果与理论值之间误差具有随机性.通过式(4)可推导得出,蒙皮纵向挠度位移与面外均布载荷呈正比例关系:
UZ=AP+b
(5)
其中:
(6)
利用式(5)对实验数据进行了线性拟合,并将拟合斜率值与式(6)所得理论斜率汇总于表3,通过对比分析可以发现,当梁布置间距分别为3、6、9 mm时,实验结果与理论结果的相对误差在20%的可接受范围内,证明了蒙皮面外弯曲性能理论模型具备设计参考价值.
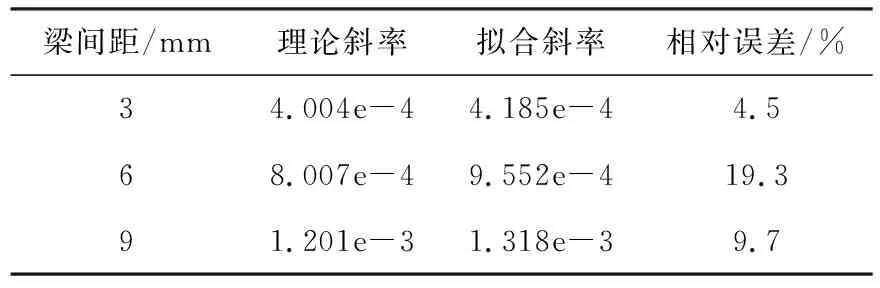
表3 柔性蒙皮理论与实验误差对比
5 结论
本文研究了一种适用于变后掠翼的刚柔耦合蒙皮,并分别对其进行了面外弯曲参数化建模、有限元仿真分析和实验测试,主要结论如下:
(1)所研究的柔性复合蒙皮由内嵌梁和纤维束将硅橡胶内部均匀划分成棋盘式网格结构,通过缩减单元尺寸比例值以提高结构稳定性;
(2)基于连续梁理论,建立了蒙皮面外弯曲参数化模型,推导出支撑梁结构尺寸、材料参数、布置间距以及面外压强与蒙皮纵向挠度值的关系式.利用上述参数变量对柔性复合蒙皮进行了多组数值分析.结果表明各工况仿真值与对应理论曲线吻合度程高、趋势一致,验证了所推导理论模型的可靠性.同时,由曲线变化趋势可推断出梁截面直径参数是影响蒙皮面外承载刚度的主要因素;
(3)对柔性复合蒙皮进行了静力承载测试,实验结果与理论值误差低于20%,有效说明了面外弯曲性能参数化模型具备设计参考价值.

