基于自适应预测校正的月球软着陆制导控制方法*

胡 军, 周 敬

(1.北京控制工程研究所·北京·100094；2.北京宇航系统工程研究所·北京·100076)

0 引 言

在执行载人登月或某些无人月球探测任务时，需要使飞行器在月球表面软着陆，以保证航天员和仪器设备的安全。软着陆是指飞行器在落向月面的过程中采用制动发动机进行减速，以使到达月面时的速度接近于零(一般为几米每秒)，实现安全着陆。软着陆技术是探月任务中的一项关键技术，在软着陆过程中，除了要求飞行器达到所需的着陆速度外，还要满足以下要求：1)燃料消耗最优或次优,由于月面没有大气层，软着陆过程中的制动减速只能依靠飞行器的轨控发动机来实现，这一过程会消耗所带燃料的3/4,因此，有必要设计燃料最优制导律使得燃料消耗最省，以增加有效载荷，降低发射成本；2)鲁棒性,在软着陆过程中存在初始导航误差、环境扰动、敏感器测量误差、发动机参数误差等不确定因素，因此探测器要实现软着陆，制导律必须具有鲁棒性；3)实时性,由于整个软着陆过程时间短，探测器的状态量和参数变化快，这就要求制导律具有实时性。

对于不同的探月任务，软着陆过程可能包含若干不同的阶段，但主要包括主减速段、接近段和最终着陆段等阶段，其中主减速段对最终着陆精度起决定性作用。因此，月球软着陆过程研究的重点在于主减速段制导与控制方法的研究。

目前，关于月球软着陆的制导方法主要可以分为以下几种：1)重力转弯制导方法，其基本思想是通过姿态控制系统,将制动发动机的推力方向与着陆器的速度矢量反方向保持一致，进行制动减速，最终垂直到达月面；2)标称轨道制导方法，指预先确定一条标称轨道，然后将着陆器的位置、速度的测量信息与其进行比较，生成制导控制量，使着陆器跟踪标称轨道的制导方法；3)显式制导方法，根据飞行器的实时运动参数，按控制泛函的显函数形式实时计算制导控制量的制导方法；4)摄动制导方法，同样需要预先确定一条标称轨道，然后在其附近利用一阶泰勒展开方法对轨道约束函数进行求解，将非线性动力学方程线性化，在此基础上可以较方便地进行制导律设计。

关于软着陆控制方法的研究主要有：王大轶等对于月球重力转弯软着陆过程，采用反馈线性化方法，对高度和速度信息分别设计跟踪制导律，并应用微分几何的有关理论证明了这两种跟踪制导系统的Lyapunov稳定性；Ruan X.G.针对软着陆过程的控制问题，提出了一种非线性动态逆与状态反馈相结合的神经元控制系统设计方案；刘兴隆基于交会对接思想，将软着陆控制问题转化为线性受限系统的二次调节问题，通过飞行器相对落点的位置和速度的状态反馈实现软着陆控制；王大轶等提出了一种基于模糊神经网络的非线性最优控制策略，使被控系统能够通过模糊神经网络的非线性映射能力实现某种最优的闭环制导控制，以实现最优月球软着陆轨迹的高精度跟踪；梁栋等采用动态平面控制技术思想，充分考虑自主制导的鲁棒性、实时性要求，以及动力下降段过程中的干扰和不确定性，实现了软着陆轨迹的跟踪；乔衍迪针对月球探测器三维精确定点软着陆问题，对动力下降段制导给出了一种参数化控制与最优参数选择相结合的方法，在此基础上将最优控制问题转化为一系列参数优化问题；张勃将零控位移偏差/零控速度偏差(Zero-Effort-Miss/Zero-Effort-Velocity，ZEM/ZEV)方法与模型预测静态规划( Model Predictive Static Programming，MPSP)方法相结合，提出了多约束的次优月面定点软着陆制导算法。在工程实践方面，对于我国“嫦娥”系列月球探测器软着陆问题，文献[14-16]基于线性正切制导律，针对主减速段提出了一种自适应动力显式制导方法，结合递推最小二乘方法，在轨估计发动机比冲、制导时间等参数，并通过终端状态和快速调整过程的预测，对制导目标进行自适应修正，以满足接近段的初始约束条件。该方法不仅实现了推进剂消耗相对较少，还提高了系统对质量、推力和比冲等不确定性的适应性。

另一方面，在与软着陆有近亲关系的航天器进入/再入过程的制导方法研究中，预测校正制导方法对初始再入位置具有很强的鲁棒性；但常规的预测校正制导方法对动力学与环境参数的偏差比较敏感，动力学与环境参数相对标称参数的变化将导致预测结果出现偏差，进而导致终端状态出现偏差，因此必须对动力学与环境参数进行在线实时估计并补偿。基于此，胡军在1998年提出了基于二阶特征模型的全系数自适应预测校正制导方法，2011—2013年杨鸣等通过嫦娥五号再入返回飞行试验器的论证、设计，以及2013—2014年胡军等通过复核复算和独立评估，发明了基于一阶特征模型的全系数自适应预测校正双环制导方法(以下简称为自适应预测制导方法)，并在嫦娥五号再入返回飞行试验器的飞行任务中(2014-11-01)获得极大的成功，之后又成功应用于新一代载人飞船试验(2020-05-08)、嫦娥五号月球取样返回探测器返回器(2020-12-17)、神舟十二号载人飞船(2021-09-17)。这一系列的成功应用和世界领先的落点精度水平，促进了自适应预测制导方法的进一步应用研究。目前完成的研究除了地球轨道直接再入、月地返回轨道跳跃式再入外，还包括火星进入与火星大气捕获、大升力体初始再入、末端能量管理、进场水平着陆，以及高超声速飞行器发射段与返回段的制导等。航天器无论处于什么环境，动力学形式都是一样的，只是参数取值不同。基于这一基本认识，自适应预测制导方法可以作为航天器的一种通用的制导方法，应用到无大气的月球软着陆上。

自适应预测制导方法是一种具有逻辑结构的构造性方法，通过如下机械性的步骤实现。

离线准备工作：

1)标称轨迹：设计一条能达到目标并满足所有约束的标称制导剖面及其标称轨迹。

2)时变动态控制增益：利用数学仿真方法，建立描述预测偏差与制导增量之间的时变动态控制增益函数。对于一些应急场景，该项工作也可放在实时在线进行。

实时在线工作：

1)关键参数估计：利用惯性测量单元原始测量和导航系统输出，估计影响飞行的关键参数：a)无大气飞行条件下，控制加速度；b)有大气飞行条件下，气动综合因子+和升阻比(为升力，为阻力)；非轴对称条件下，横向力系数。

2)自适应的轨迹预测与约束函数计算：以当前时刻至终端的制导控制量作为输入，代入影响飞行的关键参数估计结果，预测当前至终端的弹道曲线，记录/计算过程中的约束函数，求出终端状态与目标终端状态的偏差即预测偏差。

3)输入输出变换与基于一阶特征模型的自适应制导：如果约束函数满足过程约束，则将当前时变动态控制增益逆分解为预测偏差与制导增量之间的输入、输出变换。根据输入变换后的广义预测偏差、广义制导控制增量，按照一阶自适应控制方法，求下一步的广义制导控制增量，经输出变换转为实际制导控制增量。

4)约束处理：如果约束函数不满足过程约束，调用过程约束-制导控制量调整算法，给出满足过程约束的实际制导增量剖面。

5)预测制导的实际输出与预测轨迹生成：预测制导控制量 = 标称制导量 + 实际制导增量，作为预测制导的实际输出；以当前时刻至终端的预测制导控制量作为输入，代入影响飞行的关键参数估计结果，预测当前至终端的弹道曲线，按标准弹道制导所需生成相应的数组。

6)可选择的标称轨道自适应制导律：下文式(1)～式(5)的实际输出作为长周期外环，标称轨道自适应制导律作为短周期内环，实现双环制导。

相较于常规的预测制导方法，自适应预测制导方法以逐步校正的方式进行，无需迭代过程，极大减轻了星载计算机的负担，更具实际意义。上述4个工程应用采用的都是以自适应预测校正制导为外环、标称轨迹自适应制导为内环的自适应双环制导体制，双环体制的主要用途是在大导航偏差情况下缓解制导偏差，当导航准确时其作用可忽略。本文研究制动问题，不考虑导航偏差，设计和仿真中没有选择双环体制。

本文针对月球软着陆过程中制导控制量少于被控制量这一欠驱动问题，在已有的基于一阶特征模型的全系数自适应预测校正方法的基础上，将输入输出相等的系统拓展为输入少于输出的欠驱动系统，以满足对位置、速度矢量同时进行制导控制的需要。

1 月球软着陆模型

通常情况下，根据月球探测任务、制导控制方法等的不同，整个软着陆过程会划分为若干个不同的阶段，但每个阶段对应的动力学模型是完全相同的。考虑到主减速段对软着陆精度起决定性作用，故本文针对软着陆过程中的主减速段进行研究。忽略主减速段末段的不共面影响，将主减速段近似为在一个平面内飞行，建立如图1所示的极坐标系来描述着陆器的软着陆过程。该坐标系的原点位于月心，极轴指向主减速段的初始位置。同时，考虑到主减速段飞行时间较短，可忽略太阳和地球的引力摄动、月球非球形摄动和月球自转等因素，着陆器在软着陆过程中仅受到月球引力和制动发动机推力的作用。

图1 月球软着陆示意图Fig.1 The sketch map of Moon soft landing

着陆器软着陆过程的动力学模型可由如下的微分方程来描述

(1)

其中，为月心距；为极角；为径向速度；为横向速度；为推力矢量与横向速度之间的夹角；为着陆器质量；为发动机推力；为月球引力常数；为制动发动机比冲；为海平面重力加速度。

假设着陆器的初始状态为环月停泊轨道的近月点，终端状态为距月面某一高度，初始时刻为0，终端时刻自由，则软着陆段的初始边界条件和终端边界条件为

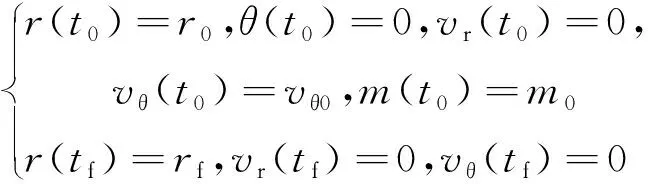
(2)

其中，为近月点处的月心距；为近月点处的轨道速度；为着陆器动力下降段起始时刻的初始质量；为终端时刻对应的期望月心距。

在获得上述软着陆动力学模型之后，为执行下一步的制导控制，需要预先给出一条标称软着陆轨道或标称(期望)终端状态。考虑到软着陆过程中的燃料最省的要求，本文采用目前应用较为广泛的Gauss伪谱法对标称软着陆轨道进行优化。鉴于目前已有相关文献大都以常推力发动机为研究背景，为方便对照，故本文中的标称软着陆轨道同样采用常推力的方式获得。同时，考虑到随着科学技术的发展,变推力发动机必将成为未来的发展趋势，故本文在后续的制导控制部分采用推力可变的方式，以生成所需的制导控制量。

因此，包含制导控制量的软着陆动力学模型为

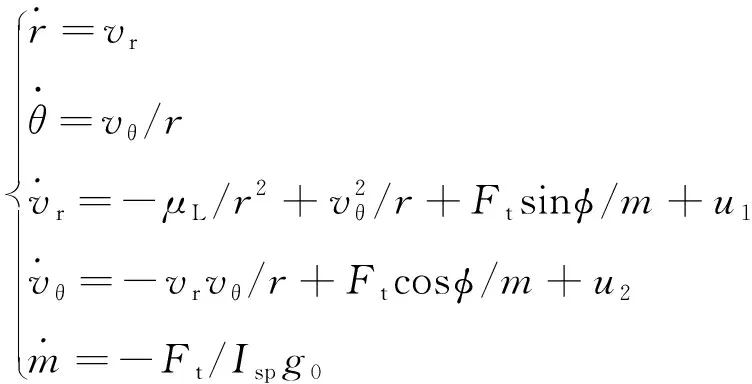
(3)

其中，=[,]为制导控制所需的控制量。

显然，根据式(3)，在实际软着陆过程中，发动机产生的推力分为两部分：一部分用于标称软着陆轨道，即[sin,cos]；另一部分用于软着陆制导控制，即[,]。因此，实际发动机推力大小′和实际推力方向角′存在如下关系

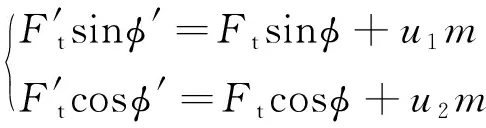
(4)

2 月球软着陆自适应全系数预测校正方法

自适应全系数预测校正方法的本质是一种积分型制导算法，可以把终端误差的修正均匀分布到当前时刻至终端时刻的整个区间内，是一种闭环无差系统，通过不断地预报和修正，最终将着陆器导引到标称终端状态。在具体实现上，在每一个制导周期内，利用动力学方程预报当前制导策略下着陆器的终端状态，并计算出其与标称终端状态之间的偏差，然后根据自适应全系数预测校正制导律获得所需制导控制量，最终实现着陆器的制导控制。

校正环节根据终端状态偏差计算出所需制导控制量，需要已知制导改变量与终端状态改变量之间的映射关系。解决方法如下：从终端时刻往前度量，对制导指令人为地施加一定的改变量，这必然引起终端状态的改变。在相同的改变量下，施加得越早，对终端状态的影响就会越大。基于此原理，在终端时刻前的不同时刻，在标称制导量的基础上施加某一固定的增量，然后采用数值拟合的方法，便可获得制导改变量与终端状态改变量之间的特征关系。

图2给出了制导改变量(即控制量)分别设置为[0.001,0.001]和[-0.001,-0.001]时终端状态的改变量随时间的变化关系。可以看出,4个终端状态误差随时间单调变化，增量施加得越早，对终端状态的影响越大，且具有保号性。同时，对于正的制导增量，终端状态产生正的改变量，对于负的制导增量，终端状态产生负的且大小几乎相同的改变量，因此还具有对称性。这为自适应全系数预测校正方法在软着陆制导控制问题上的应用奠定了良好基础。

(a) 制导增量设置为[0.001,0.001]T时

定义：预测的终端状态误差与制导增量之比定义为时变动态增益()。

自适应全系数预测校正方法将终端状态偏差与制导修正量的关系用一阶特征模型表示的时变动态系统来描述，然后在线估计一阶特征模型的系数。为了应用自适应全系数理论，基于定义中的时变动态增益对制导控制系统进行输入输出变换，可使动态增益的范围大幅度减小。图3所示为自适应全系数预测校正方法系统框图。

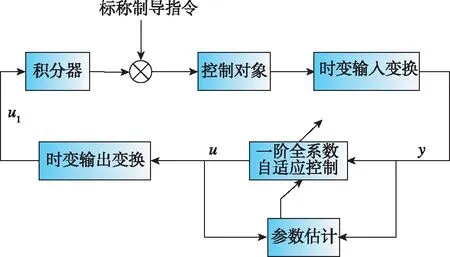
图3 自适应全系数预测校正方法系统框图Fig.3 The system chart of adaptive all-coefficient predictor-corrector guidance method

假设当前时刻对应的预测终端状态为[(),(),(),()]，标称(期望)终端状态为[,,,]，二者之间的偏差即为预测终端状态误差()，故有

()=[(),(),(),()]-[,,,]

=[Δ(),Δ(),Δ(),Δ()]

(5)

假设时刻对应的制导修正量表示为

()=[(),()]

(6)

根据自适应全系数预测校正方法，制导修正量()与预测终端状态误差(+1)之间的关系可用如下的一阶变系数差分方程表示

(+1)=()()+()()

(7)

其中,()为上述系统的4×4维系统矩阵；()为上述系统的4×2维控制矩阵。

在制导律设计中，可以利用梯度法对矩阵()和()进行在线辨识。具体地，需要按照每一个状态变量的通路分别对系统矩阵()和控制矩阵()中的行元素进行辨识，具体如下：

对于()中第个元素()，定义回归向量为

()=[(-1);(-1)]

(8)

待估计的参数向量为

()=

[,1(),…,,4(),,1(),,2()]

(9)

假设()的估计值表示为

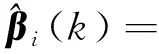
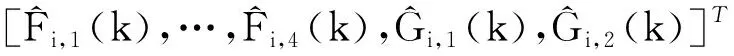
(10)

利用如下的梯度法辨识参数()

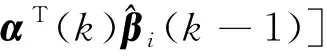
(11)

式中，和为正常数。在工程应用中，特征模型中参数的取值范围可根据特征模型理论给出。

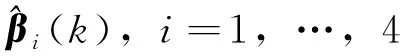
该方法相较于传统的预测校正方法，避免了迭代过程，每个制导周期只进行一次自适应控制计算，然后采用如下的线性反馈控制方法得到制导指令的修正量()。

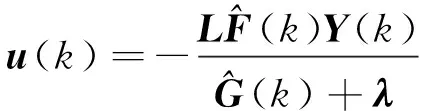
(12)

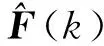
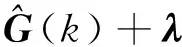
对于本文研究的月球软着陆问题，根据自适应预测校正控制器(12)，将每个制导周期内的4维终端状态误差代入式(12)，便可以得到2维的控制器输出，由此便实现了2维控制量对4维状态量的欠驱动控制，同时也将自适应预测校正控制方法由输入输出维数相等的系统拓展为输入维数少于输出维数的欠驱动系统。

为全面分析该制导控制方法的性能，下面针对三类场景进行仿真分析，即位置矢量制导控制、速度矢量制导控制、位置速度矢量同时制导控制。

3 仿真校验

为验证本文方法的有效性，对月球软着陆的主减速段进行仿真分析。考虑到真实月球软着陆问题，为给后续精确制导控制留有操作空间和余量，本文参考文献[14]将主减速段的终端高度设置为3km。同时，为便于仿真校验，软着陆的初始条件选自文献[11]。发动机推力=6500N，比冲=300s，月球引力常数=49028026km/s。着陆器的初始状态的取值及偏差情况如表1所示。

表1 软着陆初始状态

为得到标称软着陆轨迹，采用Gauss伪谱法对软着陆轨迹进行优化，得到的标称软着陆状态和最优推力方向角的时间变化曲线如图4所示。

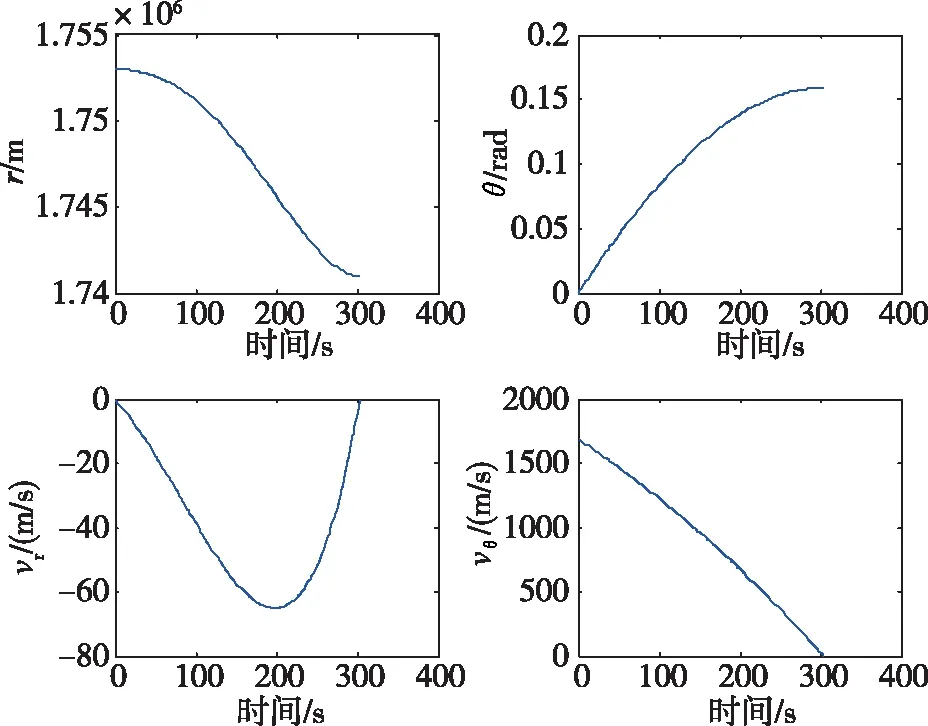
(a) 各状态的时间变化曲线

在获得标称软着陆轨迹之后，便可以对主减速段进行预测校正制导控制。令主减速段初始状态的导航偏差为表1中误差范围内的任意取值，同时，为进一步分析此方法对质量、推力和比冲具有不确定性时的适应性，在仿真过程中在初始状态误差的基础上对动力学模型中的推力、质量和比冲均进行±20%的拉偏处理，具体结果如下所示。

3.1 位置矢量制导控制

针对此问题，制导控制量[(),()]仅对位置矢量[(),()]进行制导控制。基于此，式(5)～ 式(12)中的终端状态仅取()=[(),()]-[,]=[Δ(),Δ()]即可，仿真结果如图5和图6所示。

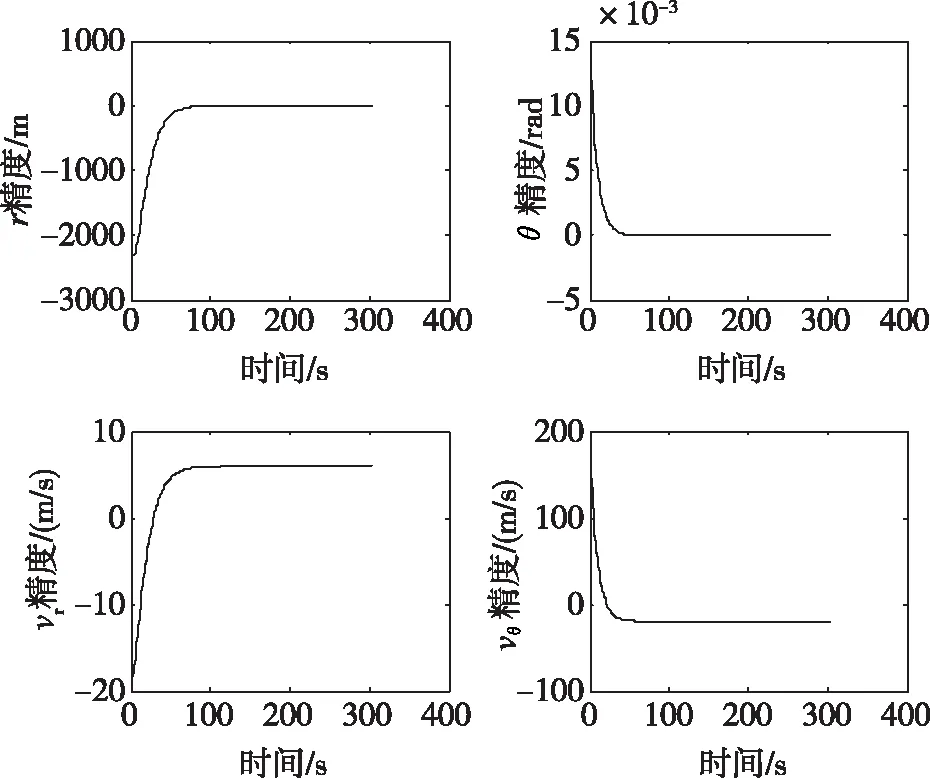
(a) 终端状态误差收敛情况

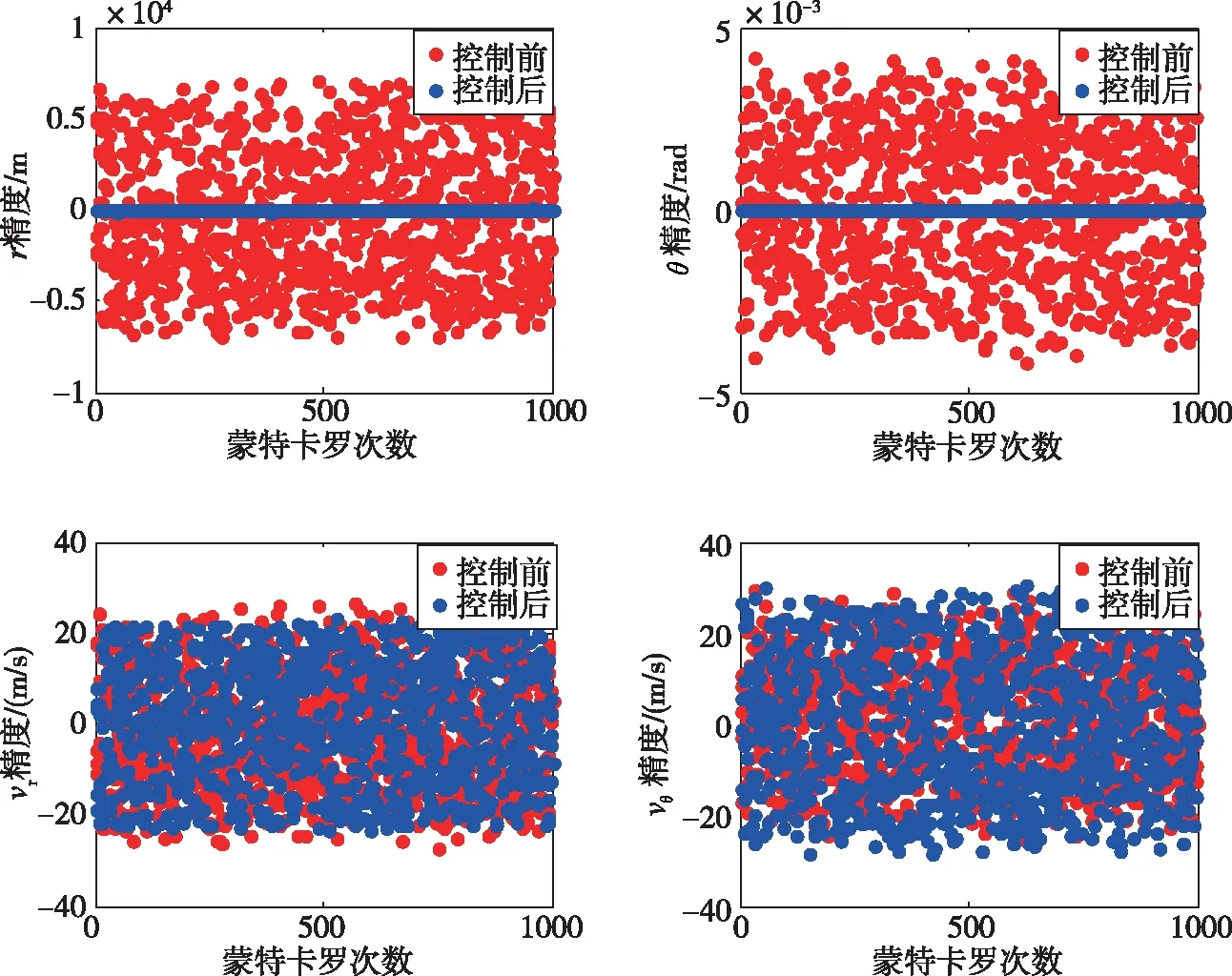
图6 考虑初始状态误差、推力偏差、质量偏差以及比冲偏差下的1000组蒙特卡罗仿真下的终端状态精度改进情况Fig.6 The improvement of precision in the 1000 Monte Carlo simulations considering the initial state error, thrust error, mass error and specific impulse error

从图5(a)中可以看出，当同时考虑初始状态误差、推力偏差、质量偏差以及比冲偏差时，经过预测制导控制，主减速段的位置矢量的终端状态误差收敛至零附近，但速度矢量出现了过控制的现象；从图5(b)中可以看出，经过预测制导控制，随着主减速段过程的进行，实际的软着陆下降轨道的位置矢量收敛至标称(期望)终端状态，但速度矢量没有收敛至标称(期望)终端状态；图5(c)为控制量变化曲线，可以看出，主减速段的制导控制过程仅在开始后的一小段时间内需要相对较大的控制量，此后阶段产生的控制量较小，接近于零。这表明，利用自适应全系数预测校正方法仅需要较小的控制量，便可以实现主减速段的位置矢量高精度制导控制。

从图6中可以看出，经过1000组的蒙特卡罗仿真，在制导控制后，月心距的终端精度范围为[-96.3,99.6]m，均值为-8.7×10m；极角的终端精度范围为[-9.8,4.5]×10rad，均值为-1.7×10rad；径向速度的终端精度范围为[-23.4,23.3]m/s，均值为0.8m/s;横向速度的终端精度范围为[-28.2,30.67]m/s，均值为0.4m/s；位置矢量达到了月球软着陆精度要求。经过统计，各终端状态的精度提高倍数分别为1.7×10、6.2×10、1.7、1.4。

3.2 速度矢量制导控制

针对此问题，制导控制量[(),()]仅对速度矢量[(),()]进行制导控制。基于此，式(5)～式(12)中的终端状态仅取()=[(),()]-[,]=[Δ(),Δ()]即可，具体仿真结果如图7和图8所示。

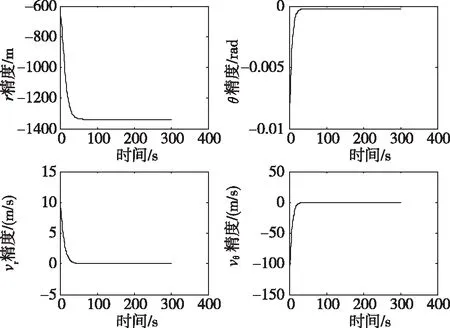
(a) 终端状态误差收敛情况

图8 考虑初始状态误差、推力偏差、质量偏差以及比冲偏差下的1000组蒙特卡罗仿真下的终端状态精度改进情况Fig.8 The improvement of precision in the 1000 Monte Carlo simulations considering the initial state error, thrust error, mass error and specific impulse error

从图7(a)中可以看出，当同时考虑初始状态误差、推力偏差、质量偏差以及比冲偏差时，经过预测制导控制，主减速段的速度矢量的终端状态误差收敛至零附近，但位置矢量出现了欠控制的现象；从图7(b)中可以看出，经过预测制导控制，随着主减速段过程的进行，实际的软着陆下降轨道的速度矢量收敛至标称(期望)终端状态，但位置矢量没有收敛至标称(期望)终端状态；图7(c)为控制量变化曲线，可以看出，主减速段的制导控制过程仅在开始后的一小段时间内需要相对较大的控制量，此后阶段产生的控制量较小，接近于零。这表明，利用自适应全系数预测校正方法仅需要较小的控制量，便可以实现主减速段的速度矢量高精度制导控制。

从图8中可以看出，经过1000组的蒙特卡罗仿真，在制导控制后，月心距的终端精度范围为[-3202.3,3342.3]m，均值为-13.1m；极角的终端精度范围为[-2.2,2.2]×10rad,均值为-9.2×10rad；径向速度的终端精度范围为[-0.11,0.18]m/s，均值为7.8×10m/s；横向速度的终端精度范围为[-0.25,0.94]m/s，均值为4.6×10m/s；速度矢量达到了月球软着陆精度要求。经过统计，各终端状态的精度提高倍数分别为2.65、2.85、8.6×10、2.0×10。

3.3 位置、速度矢量同时制导控制

针对此问题，制导控制量[(),()]对位置矢量[(),()]和速度矢量[(),()]同时进行制导控制。基于此，式(5)～式(12)中的终端状态取()=[(),(),(),()]-[,,,]=[Δ(),Δ(),Δ(),Δ()]。具体仿真结果如图9和图10所示。

从图9(a)中可以看出，当同时考虑初始状态误差、推力偏差、质量偏差以及比冲偏差时，经过预测制导控制，主减速段的()、()的终端状态误差收敛至零附近，()、()的终端状态误差虽然没有收敛至零附近，但依然实现了精度的提升；从图9(b)中可以看出，经过预测制导控制，随着主减速段过程的进行，实际的软着陆下降轨道的()、()收敛至标称(期望)终端状态，但()、()没有完全收敛至标称(期望)终端状态；图9(c)为控制量变化曲线，可以看出，主减速段的制导控制过程仅在开始后的一小段时间内以及最终时刻需要相对较大的控制量，其余阶段产生的控制量较小，接近于零。这表明，利用自适应全系数预测校正方法仅需要较小的控制量，便可以实现主减速段的位置、速度矢量的有效制导控制。

(a) 终端状态误差收敛情况

从图10中可以看出，经过1000组的蒙特卡罗仿真，在制导控制后，月心距的终端精度范围为[-3226.5,3321.3]m，均值为18.3m；极角的终端精度范围为[-2.3,2.1]×10rad,均值为-1.4×10rad；径向速度的终端精度范围为[-0.25,0.24]m/s，均值为-9.8×10m/s；横向速度的终端精度范围为[-0.51,0.56]m/s，均值为3.3×10m/s；位置、速度矢量基本达到了月球软着陆精度要求。经过统计，各终端状态的精度提高倍数分别为2.68、6.98、159.6、654.7。

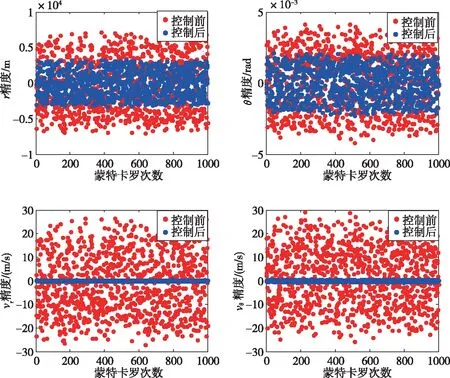
图10 考虑初始状态误差、推力偏差、质量偏差以及比冲偏差下的1000组蒙特卡罗仿真下的终端状态精度改进情况Fig.10 The improvement of precision in the 1000 Monte Carlo simulations considering the initial state error, thrust error, mass error and specific impulse error

综合上述仿真分析结果，当2维的制导控制量[(),()]单独对2维的位置矢量[(),()]或速度矢量[(),()]进行制导控制时，均具有极高的精度；当对4维的位置、速度矢量[(),(),(),()]同时进行制导控制时，制导控制精度相比前者提升有限，这是由欠驱动的物理本质所决定的，但依然具有一定的有效性。

本文提出的自适应全系数预测校正方法可以有效解决月球动力下降段的制导控制问题，且具有较高的精度和较强的鲁棒性。

4 结 论

针对月球软着陆过程中的制导控制问题，本文给出了一种基于一阶特征模型的自适应全系数预测校正方法。在经典的自适应全系数预测校正方法的基础上，对制导控制系统进行了扩维，实现了制导控制由输出相等的系统拓展为输入少于输出的欠驱动系统。仿真结果表明，本文方法可有效用于月球软着陆的制导控制，能够有效提高月球软着陆的制导控制精度，且具有较强的鲁棒性。

本文研究了初始状态误差、推力偏差、质量偏差和比冲偏差情况下的月球软着陆制导控制问题，但实际的月球软着陆过程还需进一步考虑环境扰动、敏感器测量误差等因素，这部分内容可作为未来研究方向。