速度相关初制导拐弯规律设计*

郑国栋，石 琛，韦亚利，王 磊

(1.南京理工大学 自动化学院·南京·210094；2.上海机电工程研究所·上海·201109)

0 引 言

初制导的任务是实现向目标射向拐弯，使初制导段结束时刻导弹姿态、速度达到射向要求。而地面发射的导弹，初制导段的任务还包括完成姿态控制到过载控制的交班，一般来讲，导弹马赫数达到 0.8以上，认为具有过载控制能力。文献[3]针对初制导大拐弯，提出了一种基于最优控制理论的最优拐弯方法，使拐弯完成时导弹的末端速度最大。文献[4]分析了用于垂直发射防空导弹初制导的三角型和指数型两种导引控制，结果表明，指数控制律的弹道倾角误差、最大攻角和速度损失均较小，其导弹交班精度更高。文献[5]对便携式红外寻的防空导弹的初制导进行了研究，在侧向力控制条件下给出了发射时下沉的补偿措施。文献[6]提出了一种适合初制导律的剩余时间拟合方法。文献[7]利用粒子群算法和变尺度法，完成了初制导拐弯规律的优化。文献[8]提出了一种基于自适应滑模观测器的终端角度约束制导律。文献[9]应用遗传算法对防空导弹垂直发射转弯程序进行了优化设计。文献[10]应用最小时间控制理论，研究了采用燃气舵控制的防空导弹全方位快速姿态调转技术。

但现有研究大部分针对推重比大的防空导弹，无需考虑姿态控制切换到过载控制的速度需求，其主要工作是做到时间和能量的最优。针对远程防空导弹采用推重比小的助推发动机，具有导弹加速慢、不同环境温度下初制导段时间长且散布大等特点，为了减小初、中制导段交班时导弹飞行状态散布，提高姿态、速度方向到位精度，本文对传统防空导弹初制导拐弯规律进行了改进设计。

由于助推发动机推力性能散布大，导致初制导段时间散布大，因此与时间相关的拐弯规律不再适用。本文寻求一种与速度相关的拐弯规律，并针对初制导时间长造成重力影响速度到位精度的现象，给出了一种含重力补偿的初制导拐弯规律，用于解决初制导段导弹姿态、速度方向的精度控制问题。

1 与速度相关的拐弯规律

记录起控开始时刻导弹纵轴向量(,,)，求取初制导结束时刻期望纵轴向量(,,)，则两纵轴向量夹角为

ϑ=arccos(++)

(1)

设计一种与速度相关的纵轴向量夹角变化规律ϑ

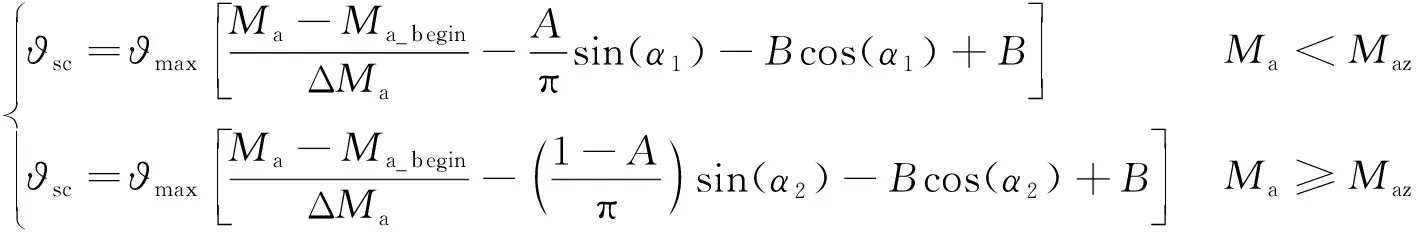
(2)

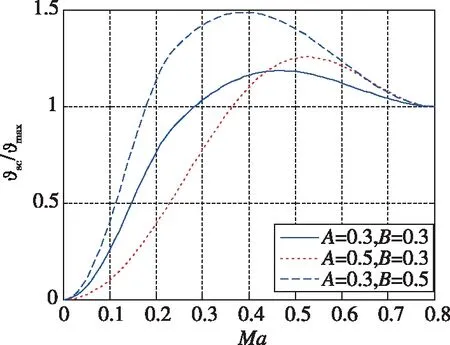
图1 与速度相关的纵轴向量变化规律Fig.1 Regulation of y-axis vector with velocity

其中，主要影响指令上升的速度，主要影响指令的最大值。通过调节、的大小，可以调整指令变化的规律，使导弹在其弹体操纵性条件下，尽可能快地完成拐弯，同时避免太大的超调造成攻角超限影响其稳定性。

构建一个坐标系，使得纵轴向量的变化可以在该坐标系的一个坐标平面内描述。该坐标系的轴向量为起控开始时刻导弹纵轴向量(,,)；轴向量(,,)垂直于两纵轴向量组成的平面；轴向量(,,)由右手定则给出。

因此，构建的坐标系与地理坐标系的转移矩阵为

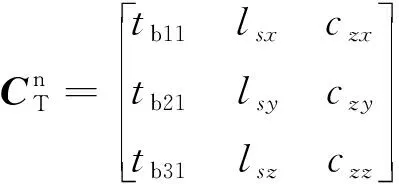
(3)

(4)

可得到弹体姿态误差俯仰指令Δϑ和偏航指令Δ

(5)

2 拐弯规律中的重力补偿项

在分析重力影响时，往往将重力投影到弹道坐标系上进行分析。同理，进行重力补偿项设计时，也在弹道坐标系下进行。设计一种姿态指令ϑ，用于补偿重力

ϑ=(,,,,)cos

(6)

(,,,,)=

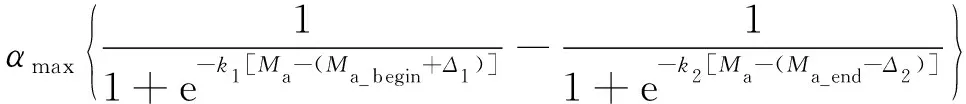
(7)

其中，为弹道倾角;、、、、为设计参数。表征为了克服重力加速度而应付出的攻角;、表征指令上升(下降)速度;、表征指令上升(下降)到最大值的一半时距开始(结束)状态的远近。取一组参数值为例，得到重力补偿项随马赫数变化规律，如图2所示。

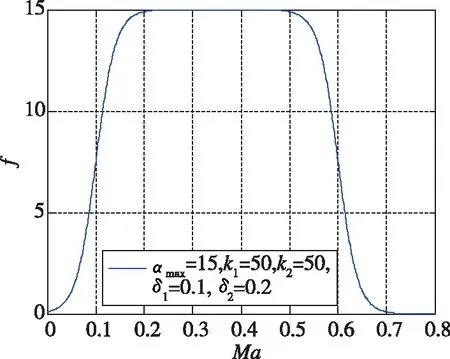
图2 重力补偿项随速度变化规律Fig.2 Regulation of gravitational compensation with velocity

设计时应选择合适的参数，避免起控时刻指令过大而弹体操纵性不够引起的稳定性下降，同时保证重力补偿效果能够消除长时间重力作用带来的速度方向变化。

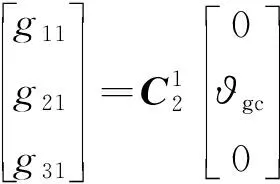
(8)

经综合，可以得到含重力补偿项的弹体姿态误差俯仰指令Δϑ和偏航指令Δ

(9)

3 仿真校验

为校验含重力补偿的速度相关初制导拐弯规律在解决助推发动机推重比小、推力性能散布大导致的到位精度差问题上的有效性，现给出仿真算例。

选取初始俯仰角70°、初始偏航角0°、初始滚转角0°作为仿真初始条件；选取俯仰角60°、偏航角0°、滚转角0°作为初制导到位条件；建立六自由度导弹模型进行仿真；根据建立的仿真模型以及参数设置，仿真结果如图3～图5和表1所示。

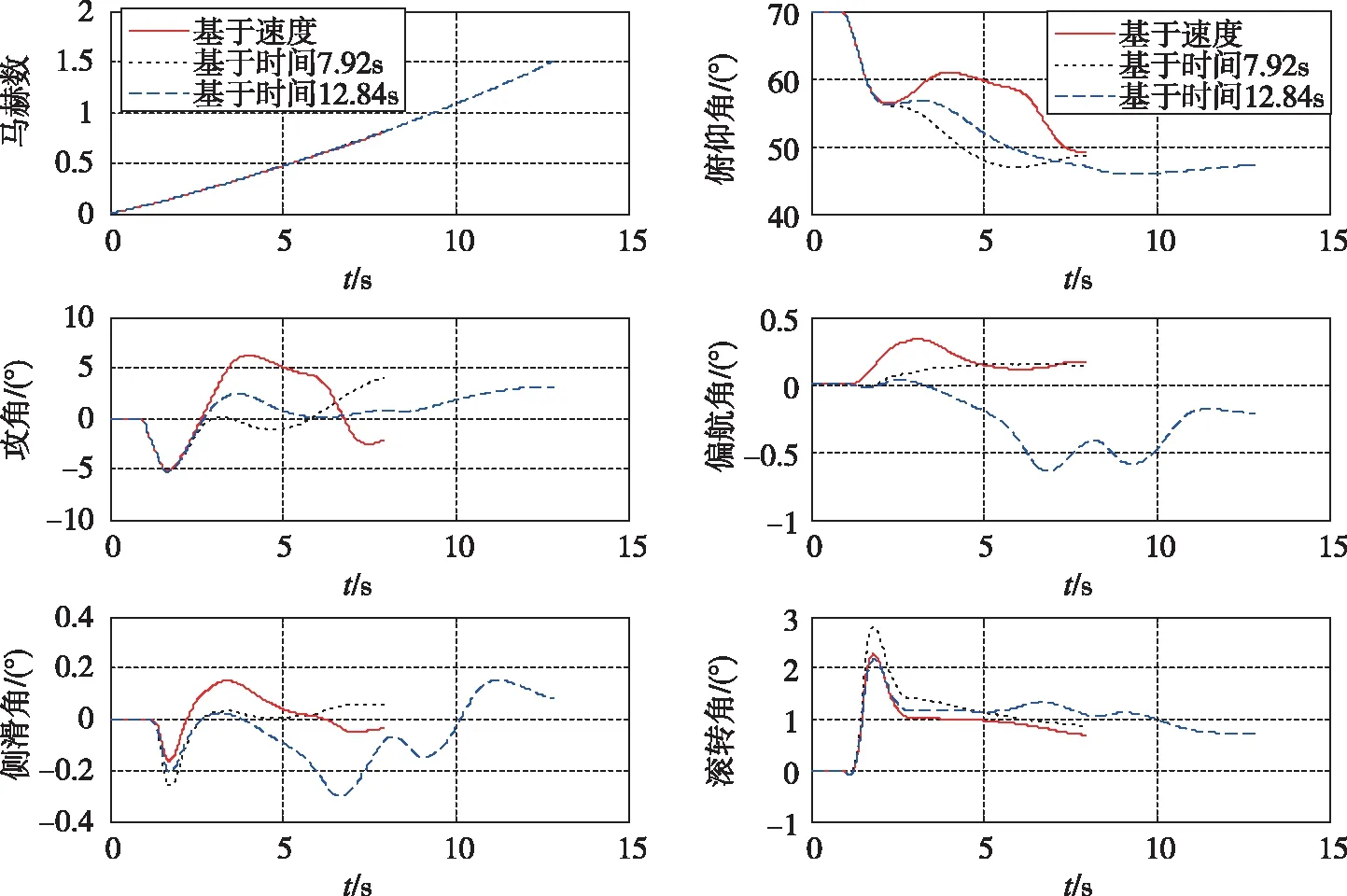
图3 高温条件下的导弹状态Fig.3 State of the missile in the high temperature

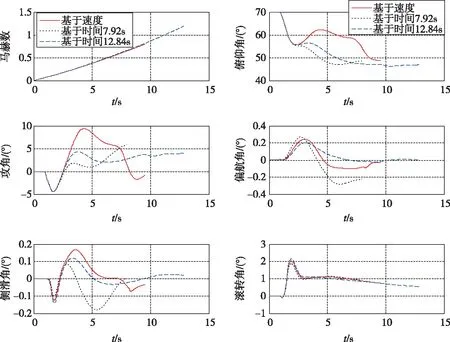
图4 常温条件下的导弹状态Fig.4 State of the missile in the normal temperature

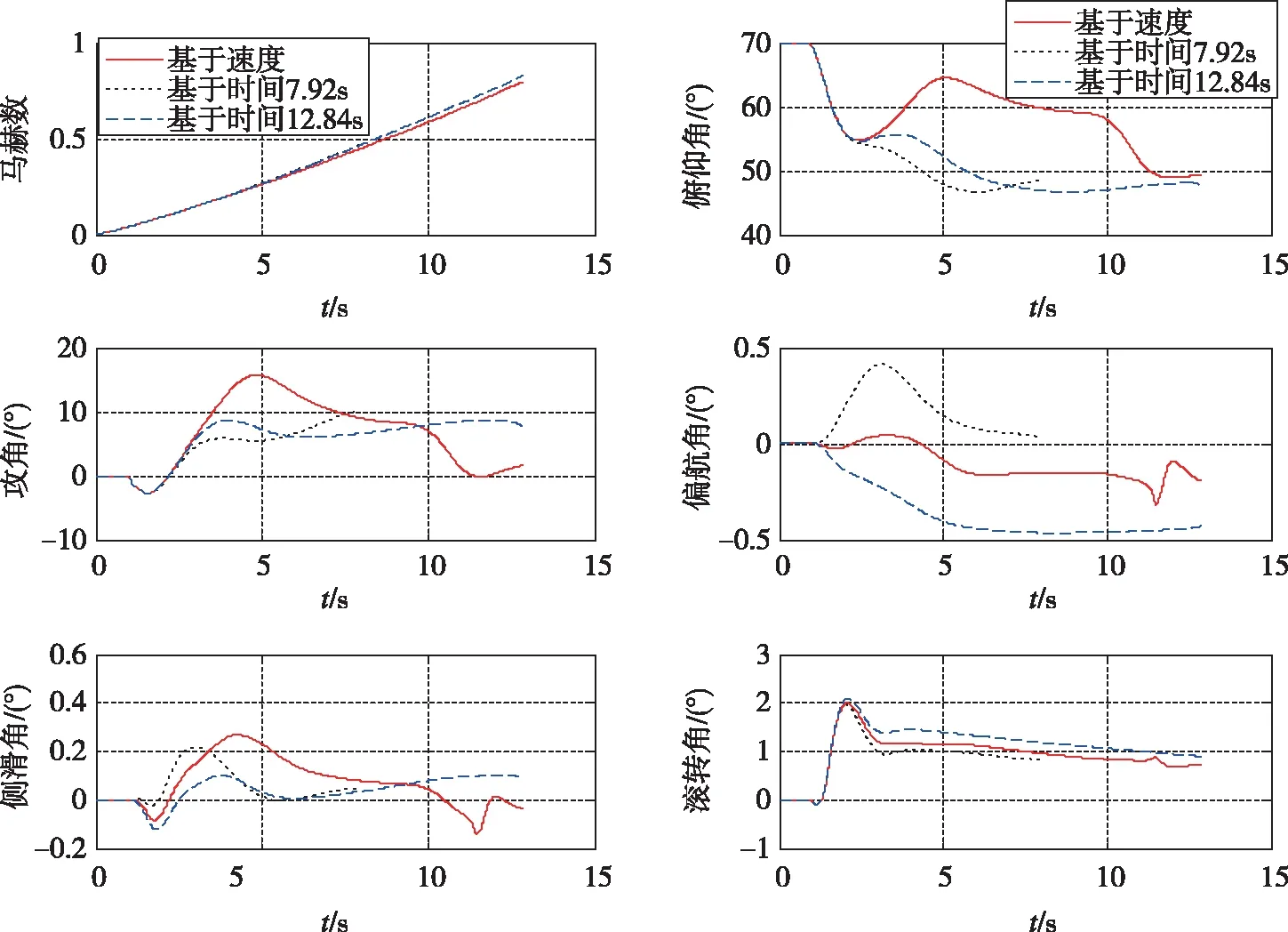
图5 低温条件下的导弹状态Fig.5 State of the missile in the low temperature

表1 仿真结果统计

由仿真结果可知：

基于时间的拐弯规律，在面对发动机推力性能散布较大的条件时，初、中制导段交班时导弹状态散布也较大。若到位时间设置较小，到位时刻速度在低温状态下只有马赫数=0.47，舵效较低，不利于初、中制导交班。若到位时间设置较大，到位时刻速度在高温状态下达到马赫数=1.50，浪费太多能量，不利于中制导段弹道的爬升；且初制导时间普遍较长，虽然姿态到位精度较好，但在重力作用下，速度到位精度差，到位时刻攻角最大达到10.14°，不利于初、中制导交班。

基于速度的拐弯规律在发动机高、常、低状态下均能较好地实现导弹的到位角度；重力补偿项的引入能够有效减小到位时刻的攻角和侧滑角，有利于初、中制导交班。

综上，基于时间的拐弯规律虽然能实现导弹的到位角，但是其初制导结束时刻的攻角和马赫数随状态变化较大，不利于初、中制导交班；基于速度加重力补偿的拐弯规律不仅能实现导弹的到位角，而且其初制导结束时刻的攻角和马赫数随状态变化较小，利于初、中制导交班。因此，基于速度加重力补偿的拐弯规律对发动机推重比小、推力性能散布大的导弹初、中制导交班更有利。

4 结 论

本文设计了一种与速度相关的初制导拐弯规律，并加入重力补偿项，能够适应助推发动机在不同环境温度下的初制导拐弯要求，减小初、中制导段交班时导弹飞行状态散布，更有利于初、中制导顺利交班。研究成果可直接应用于防空导弹初制导段指令设计。